トップページ (ヘリウムも含む正確な新ボーア模型)
Leggett
テレポーテーション "チェシャ猫" (14/8/31)
遅延選択量子消しゴムは本当か?
量子コンピューターは永遠に実現しない
このセクションの内容は、光子は粒子、それとも電磁波? と同じであるので、すでにその光子のページを読まれた方は、ベルの不等式の破れは"波"でなく"粒子"のみの局所実在性を否定できる のセクションに進んでほしい。
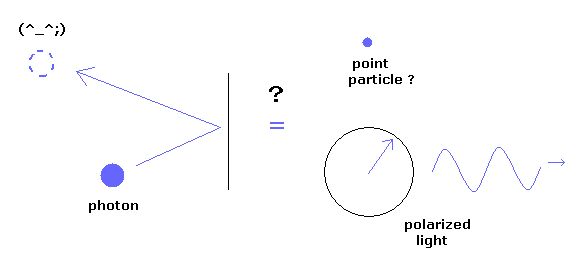
(Fig.1) 光子は 粒子 それとも 電磁波?

量子電磁力学によれば、単一光子は 点状粒子でなければならない。
しかし 実際の実験では、左、右円偏光、垂直、水平偏光の光などの 古典的な電磁波が使用されている。
彼らは 明らかに 古典的な光に特異的な性質を用いているにも関わらず 論文や何かで それを表す時 必ず 光子という粒子の表現を使おうとする。
Fig.1 に示したように、もし光が 点状の粒子だとしたら、それはどうやって 偏光したり 他の粒子と相互作用したりできるのだろうか?
つまり 光子という点状粒子の概念は 現実ではあり得ないものなのである。
(Fig.2) もつれた光子対?
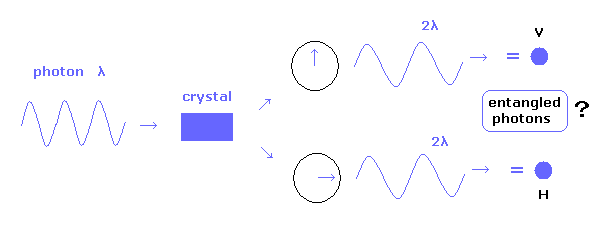
もつれた光子対は しばしば "パラメトリック下方変換" によって生成される。
この過程では 波長 λ の光子が ある結晶に入射すると、波長 2λ のペアの光子対に分離する。
そのため 全エネルギーは保存する (= それらの振動数は半分になる )。
生成された光子対の1つは 水平偏光、もう1つは垂直偏光である。
この光子対は 明らかに古典的な電磁波にも関わらず、彼らは必ず "光子"という用語を使いたがる。
(Fig.3) 光子という点粒子は 互いに干渉しあえるのか?
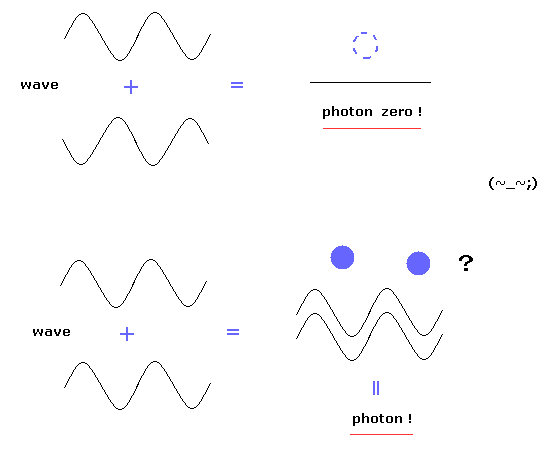
驚くことに、光子という点粒子は 彼らの実験によれば 互いに干渉し合えるのである。
Fig.3 上では、位相が逆同士の光子の干渉のため、光子は消えてしまう。
逆に Fig.3 の下では、位相がそろっている干渉のため 光子の数 (= 振幅 ) が増加すると 彼らは主張している。
しかし Fig.3 に示すように、これらの干渉現象は 彼らが言う "光子" の実態が 明らかに 古典的な波であることを示している。
(Fig.4) 単一光子検出器は 光子が粒子であることを示しているのか?
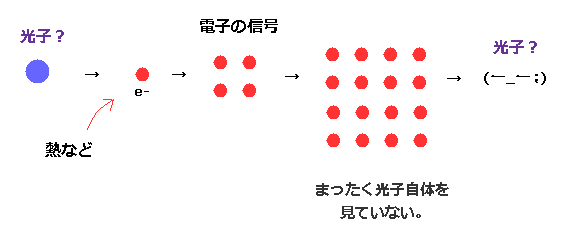
最初に 私たちは 単一の光子を直接 生成することはできない。
コヒーレントなレーザー光を弱めて 光子検出器で それらの電流信号を見ることによって、光子の存在を 推定しているにすぎない。
この検出器は 光子が入射したとき 必ず光子を検出できるわけではなく ( < 60% ) 、また dead time のため 単一光子と2つの光子の区別をつけることは不可能である。
もちろん 単一光子自体を直接見られないため、この光子という概念は 単に憶測にすぎない。
光電効果を繰り返すことによって、電流信号が増加していって はじめて 光子検出器が単一光子を検出できる。
これらの過程における光のロスを考慮すると、光の強さが ある一定の閾値に達しているとき、 光子検出器が 電流信号を示すと考えるのが 極めて自然である。
(Fig.5) マッハ・ツェンダー干渉計。
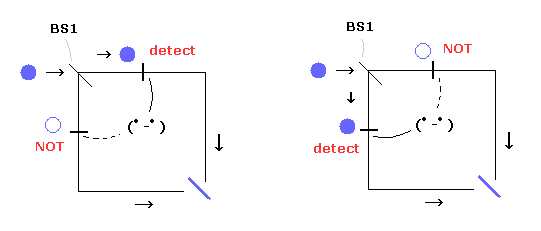
マッハ・ツェンダー干渉計では、1つの光子が ビームスプリッター (= BS1 ) で 2つの異なった経路に分離したとき、Fig.5 に示すように 同一時刻では どちらか一方の経路でのみ 1光子を観測することができる。
これはつまり 量子力学的な解釈によれば 単一光子は 2つの経路に分離していないということになる。
(Fig.6) 単一光子の干渉。
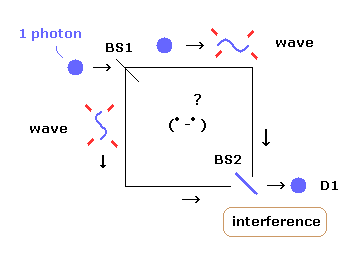
しかし これら2つの異なった経路からの 電磁波の干渉効果は 実際に観察されるのである。単一光子は 2つの経路のどちらか一方にしか存在しないはずなのに 奇妙である。
一般に この奇妙な現象は 1つの光子の 両経路への重ね合わせ現象によって生じるとされている。
この "重ね合わせ"という考えは 奇妙な多世界解釈そのものであり、はっきり言って 何のリアリティーもない。
( この場合は world A と world B ということになる。)
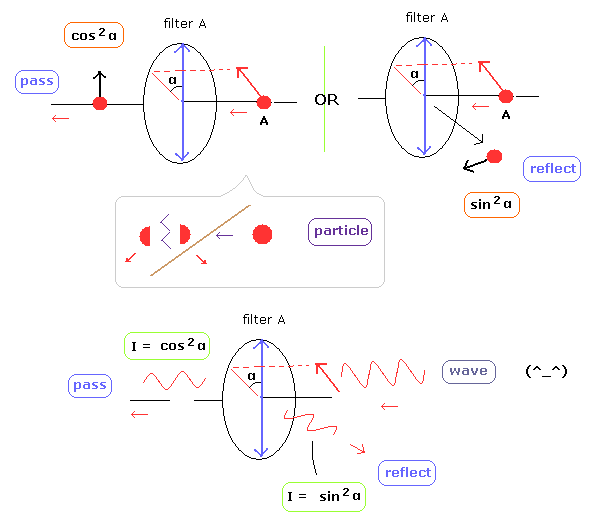
(Fig.7) 光子 = 古典的な電磁波。
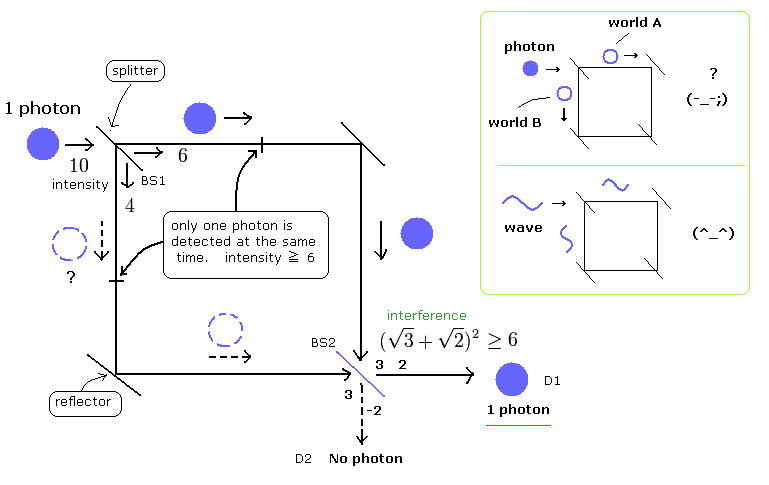
ここで光子を波として、その電磁波の強さがある一定の閾値(threshold)以上の時にはじめて光子検出器で光子1つとして認識されると仮定してみよう。
例えば、最初の1つの光子(電磁波)の強さを10としよう。
そしてそれをビームスプリッター ( BS1 ) で2つの経路に分離させるとしよう(例えば6と4に)。
そして、光子検出器では電磁波の強さが閾値6以上のときに初めて 単一光子として検出できると仮定しよう。
すると光の強さ10では光子2つ(=強さ12以上)としてではなく、光子1つとして検出されるということになる。
分離された光はというと、6サイドでは単一光子として検出でき、4サイドでは光子として検出されないということになる。
しかし、この6と4の光は干渉でき、最後に6以上になった方に光子が検出されるという、干渉効果も見事に説明できてしまう。
例えば、50/50 ビームスプリッター ( BS1 ) のとき、10の電磁波が5+5に分離された場合は両方の検出器で検出されない。
(この場合は光子の存在自体が認識されないので 無視されたケースとなる。)
光子を検出器で検出したとき はじめて、光子の存在を認識することができる。
50/50 ビームスプリッターというのは 基本的に 無偏光の光を 平均して 半分に分離するものである。
ビームスプリッター到着時点の光の偏光状態や振動数によって この確率は変化する。
(Fig.8) ビームスピリッター 2 ( BS2 )。
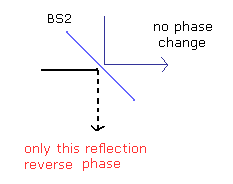
ビームスプリッター1 ( BS1 ) で分離後、ビームスプリッター2 ( BS2 ) においても 電磁波は ほぼ半分に分離される。
( 例えば、 6 → 3 + 3, 4 → 2 + 2 )
この実験では、ビームスプリッター2においては、下方向への反射のみ 光の位相が逆になるように設定されているとする。
( 通過光は変化しない。)
よって、D1の検出器側では、干渉によって 光の振幅が増加して 光子として検出することができる。
なぜなら、D1側では、光の強さが 干渉によって "必ず" 6以上に達するからである。
(光の振幅 (amplitude) は 光の強さ (intensity) の平方根であることに注意。)
[ D1側では、1光子が "必ず" 干渉によって検出される。 ]
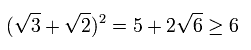
一方で、D2検出器側では、2つの経路からの 光の振幅が 互いに打ち消し合うため、光子として検出することができない。
(光の強さが D2側では、”6”に達することができない。)
[ D2 では 光子は検出されない。 ]
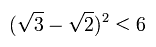
もちろん、最初の光の強度 "10" が ビームスプリッター1で 5+5 にちょうど分離された場合も 上記と同じ結果となる。
この場合は、光の強さ "5" は 2.5+2.5 にさらに分離されるため、D1側では、
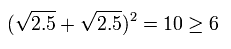
また D2 側では、
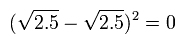
これらのケースでは、 全エネルギーが保存されている。 ( 10 → 10 ).
つまり、単一光子と複数のビームスプリッターを用いたマッハ・ツエンダー干渉計の実験は 電磁波としての光子によって十分説明可能なのである。
遅延選択量子消しゴムは本当の現象か? も参照のこと。
(Fig.9) 遅延選択実験。
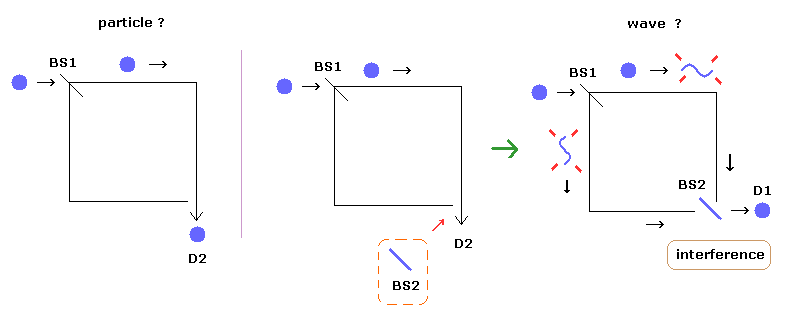
遅延選択実験によれば、単一光子が ビームスプリッター ( BS1 ) を通過後、2つの通路の片方のみに入る。
実際、光子検出器では 片方のみしか光子は検出されない。
しかし 単一光子が BS1 を通過後に 上記のように BS2 のスプリッターを通過すると、何と 両方の通路からの干渉効果が検出される。
( 光子は 片方の通路にしか入らなかったのにである。)
これは つまり 単一光子が BS1 を通過後の未来から 過去の出来事 (= 光子が波になるか粒子になるか ) を変更 (= 遅延選択 ) できることを意味しているのだろうか?
もちろん そんなことは不可能なので 光子という粒子の概念自体が間違いということになる。
( 残念ながら 一般の方々は これら奇妙な量子力学の側面をあまりご存じない。)
(Fig.10) 光子のスピンは 本当に " 1 " なのか?

1つの光子は ±1 のスピンを持つと言われている。しかし、この光子のスピン1とはいったい何なのだろうか?
一般の教科書には光子のスピン ±1 は左回転と右回転の偏光を持つ電磁波に相当すると書かれてある。そして、直線偏光はこの2つの回転偏光の重ね合わせ ( いわゆる superposition )によるとされている。
この”重ね合わせ”というのは曲者である。普通の直線偏光の光も”見方によっては”不思議な重ね合わせ状態の結果だというのだ。
つまり、”重ね合わせ”とは便利な数学的な技巧であり、いろんな場面で量子力学はごまかしのように利用している。
あるものの集合の一部分はある状態、もう一部分はべつの状態であるとき、これも重ね合わせということもできる。また、ある1つのものが目には見えない速度で振動しているときや、場合によっては単に静止しているときも”重ね合わせ”と言えなくはない。
結論からして、この”重ね合わせ”という現象は無意味以外の何物でもない。
(Fig.11) 微細構造 = 光子のスピン 1 ?
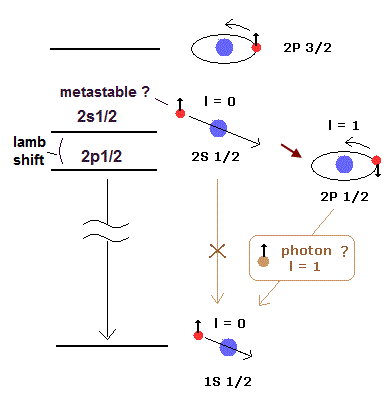
さて、そもそも光子のスピン1とはどのように発見されたのであろう?
1910 年代においては、水素原子の微細構造 は ボーア・ゾンマーフェルト模型において 2S と 2P の状態間の電子速度の違いによる相対論的エネルギーの差を表していた。
この計算結果は見事に実験値と一致していた。
電子スピンの出現以降、この微細構造の解釈がスピン・軌道相互作用(2P1/2 と 2P3/2 のエネルギーの差)に変わってしまった。このページも参照のこと。
偶然にもこの値は先のボーア・ゾンマーフェルト模型の値と一致した。(由来はまったくの別物なのに・・)。
すると、電子スピンのある水素原子では、2S から 1S への遷移は不必要になってしまい、実験値と合うようにするのは、これを抑制する必要がでてきた。
ここで、当時の研究者達は選択規則なるものを設けて、2S から 1S への遷移を勝手に抑制してしまった。そして、それは光子のスピンが1であることから説明できるとしたのだ。
すなわち、光子のスピン1とはきわめて人工的に作られたものなのだ。
(Fig.12) 点状粒子 が 光電効果 ?
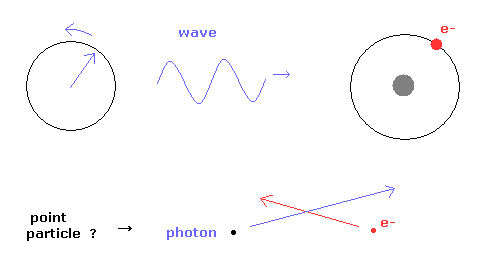
光電効果 などは、粒子としての光子でないと説明できないとされているが、果たして本当にそうだろうか?
電子は常にその周囲にド・ブロイ波 を伴い、その波は電子の運動量と同調している。
つまり、光電効果やコンプトン散乱 などの場合、小さな小さな電子よりもむしろその周囲のド・ブロイ波との相互作用を考えるべきである。
実際に 実験では 励起した原子から 円偏光もしくは直線偏光の電磁波が放射されるのを観察できる。
また 光の偉大な実験家 ラム ( ラムシフトの ) が 光子の粒子性に反対していた話は有名である。
また、最近の興味深い研究では、弱い測定によって、1光子が 電磁波(両スリットの)によって成り立っていることを示唆している。
(Science 2011, 332, 1170, S.Kocsis et al., Nature 2011, 474, 188, J.S.Lundeen et al.)
(Fig.13) 振動数 = 光子という粒子が振動している?
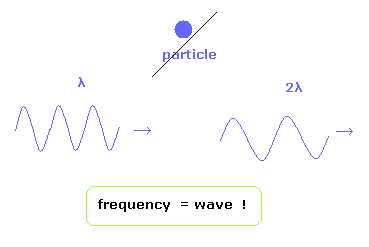
一般の教科書には 光電効果と波の振動数との関係が光子の粒子性の証明のように くどくどと書かれている。
まず第一に、振動数そのものの概念は電磁波という波の性質に基づくものであることはいうまでもない。
二つ目に、音波や波を生じる基になっている、空気や水を熱すると、それらの波を構成する各粒子の振動数は増加する。
つまり、エネルギーと振動数が密接に関係しあっていることは、しごくあたりまえの話なのである。
よって、光電効果はこのド・ブロイ波の量子化された状態の変化で説明可能である。
コンプトン効果では、もし 光が粒子だとしたら、その運動量が変化したとき、振動数のかわりに その速度 が変化するのが普通である。
上でも述べたように、振動数そのものは そもそも波の性質によることはいうまでもないことである。
(Fig.14) 便利な光子は ダークマター、エネルギー、ヒッグスなどで埋まった空間を素通りできる?
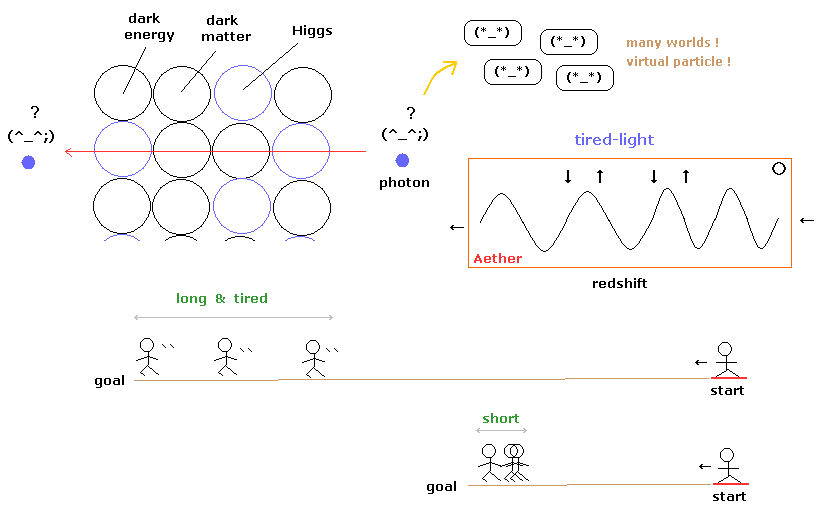
このページに示したように 光子という粒子は いろんな粒子で込み合った空間を 非常に長い期間進んでも まったく 無傷でいられる 特殊能力があることになる。
加速膨張宇宙による 赤方偏移は 空間を進むにつれて エネルギーが消失していくという "疲れた光理論" による解釈のほうが自然である。
超新星爆発からの 輝く光の期間は 遠くの星ほど長くなる。
これは マラソンランナー達と 100 メートルランナー達の 広がりの違いを思い浮かべれば容易に説明がつく。
また 光子の粒子性の概念は、 多世界解釈と 相対論に反する 仮想光子 (= クーロン力 ) を生み出す源となっている。( このページも参照のこと。 )
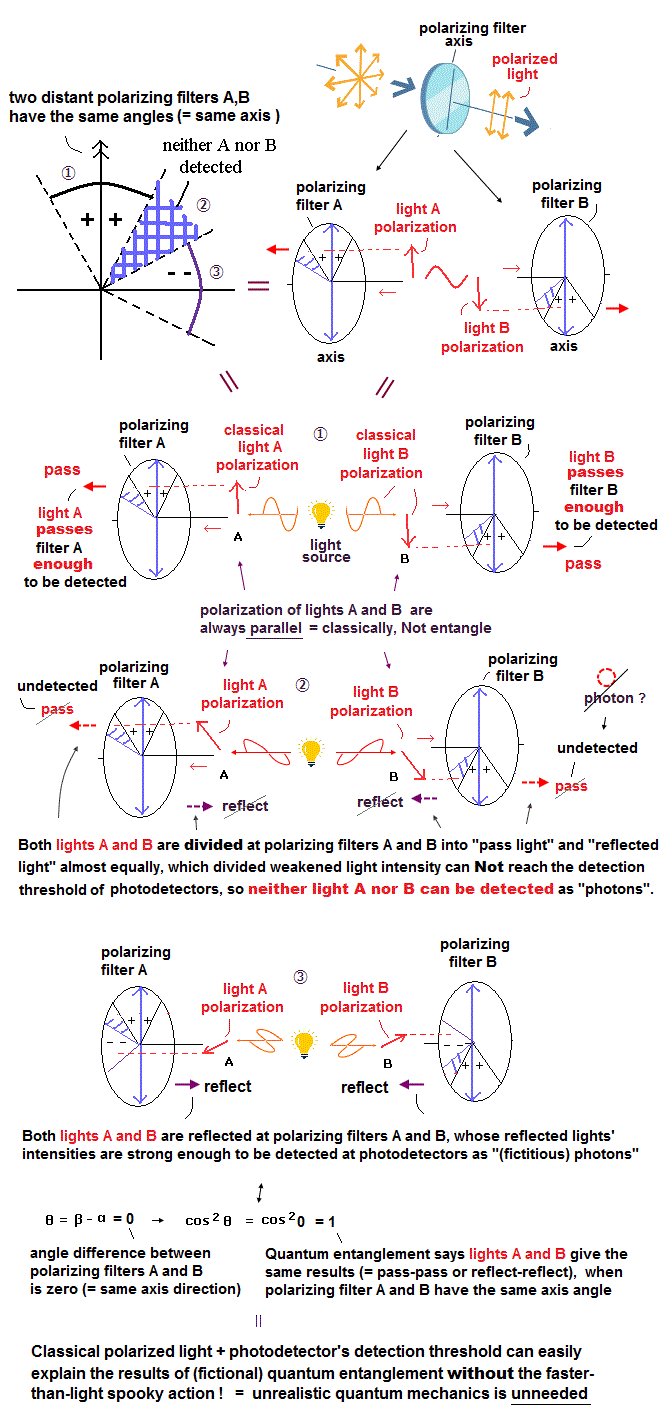
(Fig.15) 光子対のもつれ ?
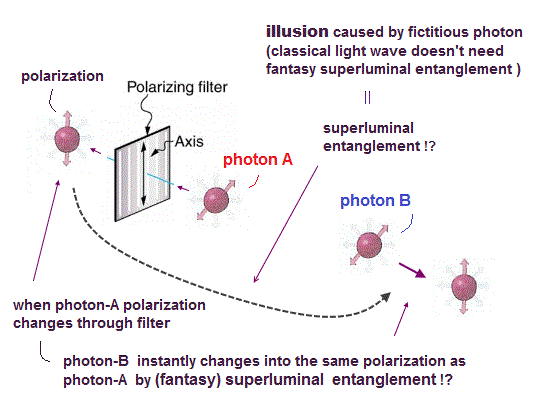
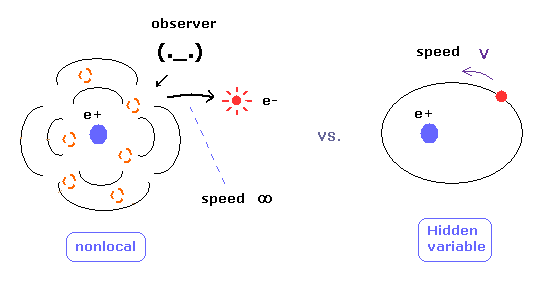
1935年、アインシュタイン=ポドルスキー=ローゼンのパラドックスが提唱され [1]、現実主義者である彼らは、 観測者が観測した瞬間に量子力学の波動関数が1点に収縮して 電子などの粒子が観測されるという奇妙な解釈を批判した。
彼らは隠れた局所変数理論 (local hidden variables theory) を提唱し、瞬時に(光速を越えて)情報が離れた場所に伝わることは不可能と考えた。
(Fig.15') 非局所性のシュレディンガー vs. 隠れた変数。
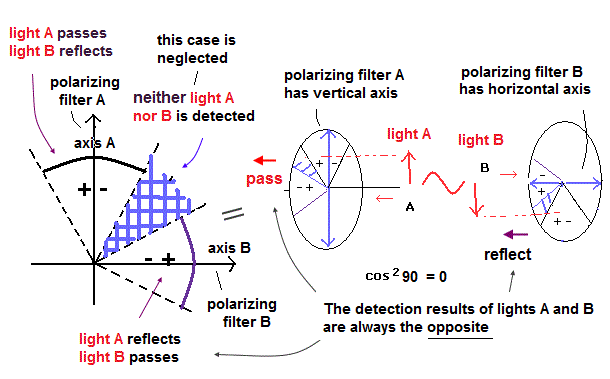
(Fig.16) ベルの不等式の破れは この現実の世界では不可能である。

1982年、アラン・アスペ が二つのペアの光子の偏光(スピン)を使った実験でベルの不等式 ( CHSH型 ) が、ある偏光板の角度では破れることを証明した [3], [4]。
この実験は何が言いたいかというと、互いに反対方向に飛んで行ったペアの光子(電磁波)の片方 (光子Aとしよう) が 偏光板 A を通過した瞬間に 超光速のシグナルが もう片方の光子 (光子B) に伝わって 離れた この光子B の偏光(電磁波の振動方向)が 偏光板 A と同じ向きに模倣してなってしまうというものである。
もちろんこの過程は光速をいくらでも超えていていい=非局所性。(瞬時だから)。
このホームページでは これら奇妙なベルの不等式の破れの実験が 光子対を利用しているところにトリックがあることを示し、古典的な電磁波のペアを使えば、古典的に実験結果を説明できることを示す。
さて、ここでは光子を電磁波と仮定して、ある一定以上の強さの光のときに単一光子として検出器で初めて認識されるという ”閾値説”を採用してみよう。
最近の興味深い実験によれば、 古典的な電磁波が その光の強度が 単一光子検出器の検出閾値より高いか低いかによって 光子であるかないかと解釈されることが示された。そして 古典的な電磁波でベルの不等式の破れの結果を模倣した。
(Ilja Gerhardt, et al. "Experimentally Faking the Violation of Bell's Inequalities." Phys. Rev. Lett. 107, 170404, 2011)
(Fig.17) 光子が通過する確率。
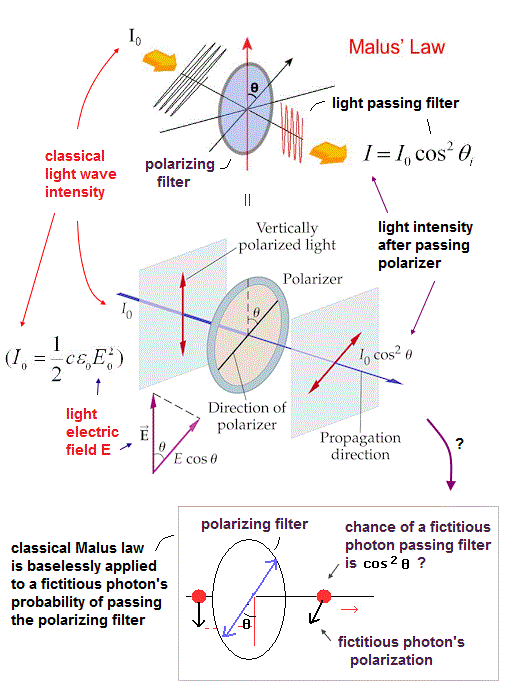
(Fig.18) フィルターにおける 単一光子の 通過 もしくは 反射の確率。
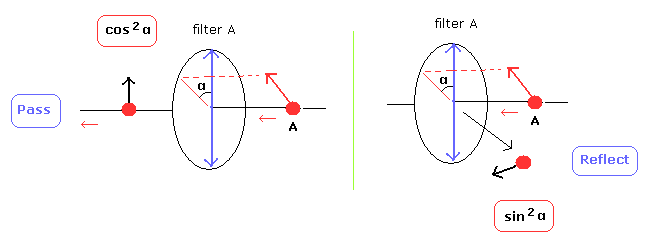
互いに正反対の(つまり互いに平行な)偏光角(スピンともいう)を持つペアの2つの光子 が放出されて正反対の方向に飛んでいるとしよう。
光子Aは偏光板Aに、光子Bは偏光板Bにぶつかるとする (= Fig.19 )。
(Fig.19) 両光子 とも偏光板 を通過する確率?
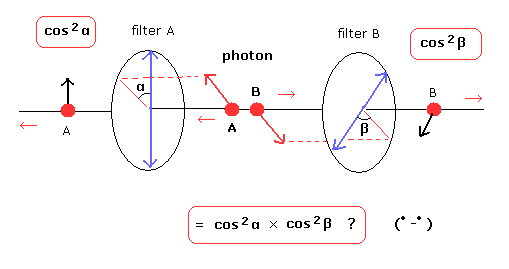
もし、光子Aと偏光板Aの角度が α のとき、光子Aが偏光板Aを通過する確率は cos2 α =(E cos α)2。
(反射の確率は sin2 α となる。)
一方で、光子Bと偏光板Bの角度が β のとき、光子Bが通過する確率は cos2 β。
(反射の確率は sin2 β となる。)
この場合、光子AとB両方がフィルターを通過する確率は、cos2 α × cos2 β となる。
これは極めて自然な結果であるように思える。なぜなら、確率 × 確率 の関係式になっているからである。
しかし、この場合はベルの不等式を満たし、実験値と異なる結果となる。
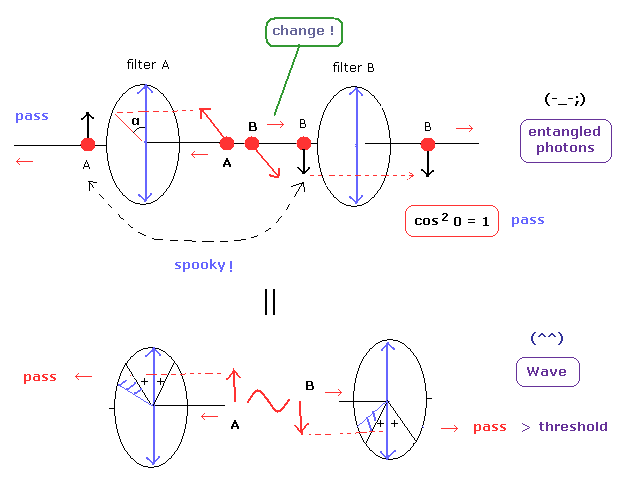
アスペなどの実験結果では、光子A が 偏光板A を通過し検出された瞬間に、光子Bの偏光角度が 遠く離れた 偏光板Aと同じになる ( Fig.20 の change ! ) とされている。
光子A が 偏光板A で反射した場合は、光子Bの偏光角は偏光板Aに垂直になる。( Fig.21 も参照のこと。)
(Fig.20) 実験結果 ( = エンタングルメント ! )
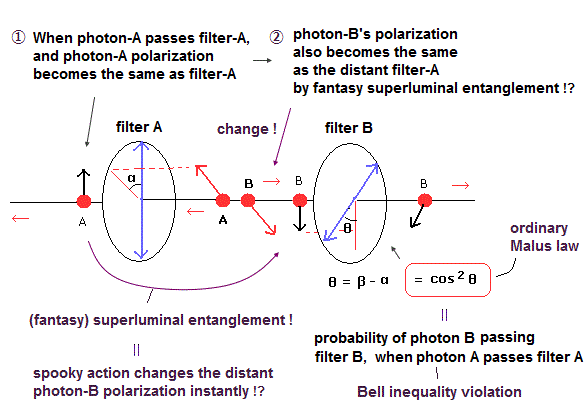
つまり、両方の光子が各偏光板を通過する確率は cos2 (β - α) になる。( cos2 α × cos2 β でない!)
( 正確には 両光子とも通過する確率は 平均 1/2 cos2 (β - α) である。 )
ここで、角度 θ = β - α は、偏光板AとBの角度差である。
この場合はある角度 θ のときに、ベルの不等式が破れる。
(Fig.21) エンタングルメントは 超光速の "spooky" なリンクによって生じる。
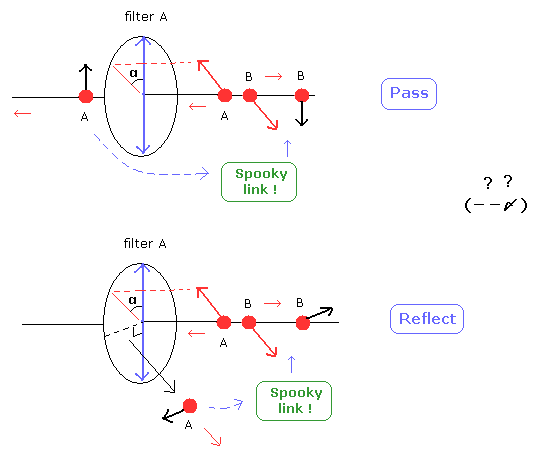
読者は この偏光フィルターの存在が どうも 特別視されすぎてると思わないだろうか ?
偏光フィルターは、全宇宙に存在する無数の物体の中の ほんの1つ にすぎないのに。
( これは 非常に都合のいい考え方と言わざるを得ない。 )
(Fig.21') 光子は分離されない。 → 波は分離する。
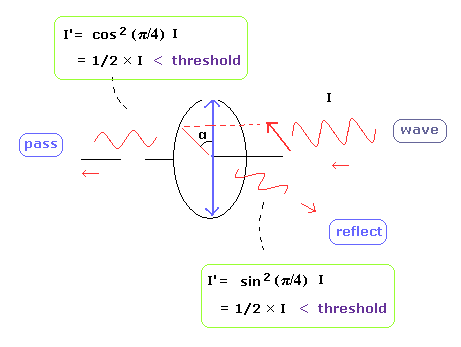
もし、光子が波ならば、通過する光子Aは偏光板Aの角度と近い角度の偏光のとき、より単一光子として検出しやすくなる(検出閾値のため)。
例えば、角 α が 約 π/4 のときは、光子 A は フィルターで 通過側と反射側の経路に等しく分解されて、通過と反射のどちらでも単一光子として検出される閾値に到達できない確率が高くなる。
なぜなら、等しく分断されたせいで、通過側と反射側のどちらの電磁波の強さも 光子検出閾値より弱くなってしまうからだ (= Fig.21'')。
( 例えば、検出器は 0.7 × I の検出閾値以上の強度の光のとき検出できると仮定してもいい。)
もし、光子AとBの両方を同時に検出できないときは、エンタングルメントの実験結果として採用されない。
(Fig.21'') 波が等しく分離される = 検出閾値に到達せず。
結果として、両方の光子が同時に検出されたとき、少なくともどちらか一方はそのぶつかった偏光板に もともと近い角度をもっていた確率が高くなるということだ。
これが、エンタングルメント (entanglement)=奇妙なリンクという幻想を引き起こす”からくり”である。
このページの2つの光子の発生源は 励起した原子を使っており、この場合は2つの光子の偏光軸は平行になる。
もし、光を垂直、水平方向の2つの光子に分離するときは、cos2 θ を sin2 θ に変更すればよい。
Malus's law を満たす限り 意味は同じである。
(もしくは、この場合も 便宜上 両方は平行とみなして、”仮ではあるが”cos2 θ の関係式を使うことは可能である。 )
(Fig.22) 偏光フィルターAとBの方向が同じ時 ( θ = 0° )
この図は、偏光フィルターAとBの角度(矢印の示す方向)が同じ場合だ ( = 0°)。
前に言ったように、光子AとBは正反対の偏光軸(つまり互いに平行な軸)を持つ。
つまり、この場合は エンタングルメントによれば、光子AがフィルターAを通過したとき、光子Bも必ず フィルターBを通過する。( = cos2 0 = 1)
ここでは 古典的な電磁波を使って、この奇妙な現象を説明してみることにする。
光子Aの偏光軸 (=光子Bも平行なため同じになる)が Fig.22の ( + + ) の方向を向いているとき、光子AとB両方とも 各フィルターを通過し、光子として検出することができる。
なぜなら、両光子の通過する光の強さともに 検出されるほど十分強いためだ (= Fig.23 )。
通過する 光の強さは I cos2α ( もしくは I cos2β ) である。
もし 光の偏光が ( + + ) の方向を向いているとき、この角度 α (もしくは β ) は 0°近い値になる。
そのため、通過する光の強さは 十分強くなるのである。
(Fig.23) 両方の波が 十分に検出されるほど 各フィルターを通過 ( ++ ) する。

しかし、光子A(=光子B)の偏光軸が Fig.22の青の部分を向いているとき、通過(もしくは反射)する両光子A、Bの光の強さは検出閾値以下であり、光子AもBも検出器で”光子”として検出することができない。(この場合は検出効率の計算にも使用されない。)
なぜなら、この角度でフィルターにあたると、通過側と反射側にほぼ等しく光が分離されて、どちらも光の強さが検出閾値に到達できなくなるからだ (= Fig.24 )。
(Fig.24) 両方の波が等しく分離される = 検出されず。

例えば、通過する光の強さは I cos2α であり、反射する光の強さは I sin2α である。
この角度 α が 45°近く (= π/4 = Fig.22 の 青の部分) のとき、通過、反射両方の強さは 1/2 × I ( 1/2 = cos2 π/4 = sin2 π/4. ) 近くになるからである ( Fig.21'' も参照のこと。)。
(Fig.24') 両方の波が 検出できるほど十分に反射される ( - - ) 。

また、光子の偏光軸が Fig.22 の ( - - ) の方向を向くとき、両光子A,Bとも十分に反射され、光子として検出することができる。
例えば、反射する光の強さは I sin2α であり、この角度 α が 90°近く (= Fig.22 の ( - - ) の部分 ) のとき、反射する光の強さは十分強くなるからだ。
つまり、この場合もペア光子の”エンタングルメントという幻想”が起こっていることになる。
(= Fig.22 では、光子AとB両方の結果が同じになる。)
(Fig.I) 古典的な光子対?

Fig.I に示すように、古典的な光子対は 通常の古典力学に従って振舞う。
( しかし そもそも古典的な光子という概念自体存在しないと思うが・・)
つまり 光子 A が フィルター A を通過したとき、光子 B は 通過 もしくは反射する。
つまり 光子 A と 光子 B の結果は 必ずしも同じにならない と彼らは主張している。
( pass - pass や reflect - reflect 以外のケースも存在する。)
(Fig.II) もつれた光子 = 古典的な波。
もつれた光子対では、光子 A が フィルター A を通過したとき、光子 B は 不気味なリンクのために 必ず フィルター B を通過する。
この非現実的な考え方を受け入れる代わりに、光子が古典的な電磁波だと考えるほうが より自然である。
すでに述べたように、検出閾値のために これらの波は 必ず同じ検出結果を示す。
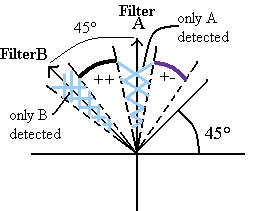
(Fig.25) フィルターAとBの間の角度が θ = 90°のとき。
次に、この図は偏光フィルターAとBの角度の差が90°のときだ。
この場合は エンタングルメントによれば、光子AがフィルターAを通過したときは、必ず光子BはフイルターBで反射する。( = cos2 90 = 0 )
光子A(=光子B)の偏光軸が ( + - ) の方向を向いているとき、光子AはフィルターAを通過し、光子BはフィルターBで反射し、両方とも検出器で光子として検出される。
(Fig.25') 光子 A は通過、 光子 B は反射する ( + - )。

しかし、偏光軸が図の青の部分を向いてるとき、光子Aも光子Bも検出閾値以下のため、光子として検出されない。
(これも、この角度だと、通過側と反射側にほぼ等しく光が分断されるからだ。)
(Fig.26) フィルターAとBの角度が θ = 45°のとき。
最後のこの図は偏光フィルターAとBの角度の差が 45° のときである。
この場合は、エンタングルメントによれば、光子AがフィルターAを通過したとき、光子BがフィルターBを通過する確率は50%だ。 ( = cos2 45 = 1/2 )
光子A(=光子B)の偏光軸が図の ( + + ) の方向を向くとき、光子AもBも両方とも各フィルターを通過し、光子として検出される。
図の ( + - )の方向のときは、光子AはフィルターAを通過し、光子BはフィルターBで反射され、両方、光子として検出される。
つまり、光子A,B両方が各フィルターを通過する確率は50%となり、予想通りとなる。
(Fig.26') 光子 A が 通過、 反射、 検出されない の各範囲。
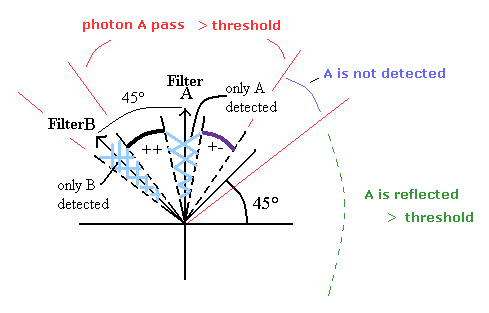
しかし、図の青の部分を向いているとき、光子AかBどちらか一つだけが光子として検出される。なぜなら、片方は通過(もしくは反射)する光の強さが検出閾値以下だからだ。
もし、2つの光子の片方だけが検出された場合は、正確な実験結果として採用されない。
なぜなら、2つの光子を同時に検出することが光子ペアがエンタングルメントしていることの必須条件だからである。
1つだけだと、ノイズとして扱われる。
実際のペア光子を使ったベルテストの実験では、光子の同時検出率(=エンタングルした光子ペアを意味する)は非常に低い。 (< 20% )
よって、ループホールのない 実験自体ほとんど不可能といっていい。
ここに示した例は cos2 θ の確率を使っているため、ベルの不等式を破る。しかし、もちろんエンタングルメントという奇妙な現象は何一つ起きていない。
つまり、電磁波という波の性質が、一つの光子の情報が瞬時にもう片方の光子に伝わるという実際では起きていない幻想を引き起こす可能性を秘めているということだ。
ここで、実際に、ベルの不等式 (CHSH 型) を計算してみることにする。
もう一つ、フィルターAとBの角度差が30°の時を追加する。
(Fig.27) フィルターAとBの角度が θ = 30° のとき。
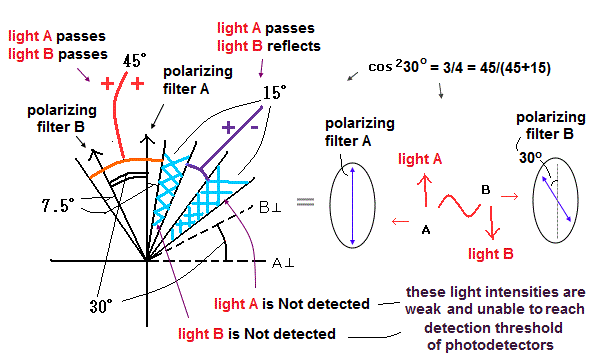
赤い部分 ( + + ) ----- 光子AとB両方とも各フィルターを通過し、検出される。
紫の部分 ( + - ) ----- 光子Aは通過し、光子Bは反射し、両方とも検出される。
斜線部分 ( 水色 ) ---- 光子Aのみ ( 通過 ) か、 光子Bのみ ( 反射 ) を光子として検出できる。(この場合は正しい実験結果として扱われない。)
この図に示すように、この場合は、光子AがフィルターAを通過し検出されたとき、光子BがフィルターBを通過する確率は、3/4 だ。( = 45/(45+15) = cos2 30 = 3/4 )。
( 60°のときは、この確率は 1/4 になる。)
ここで、ベルの不等式に関して、簡単に説明しよう。
(Fig.28) 光子 A → フィルター A1 か A2。 光子 B → フィルター B1 か B2。
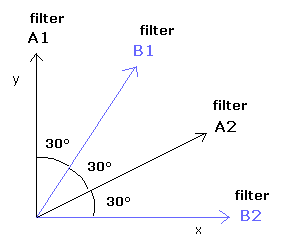
光子Aが、フィルターA1 ( 0°) とA2 ( 60°) の2種類のフィルターにぶつかり、また、光子Bも、フィルターB1 ( 30°) とB2 ( 90°) の2種類のフィルターにぶつかるとする。
Fig.28 は これら4つのフィルターの位置関係を示している。
(注意:フィルターA1とA2は 光子Aの側、フィルターB1とB2は 光子Bの側にある。)
この場合は、光子AとBが、フィルター ( A1、A2、B1、B2 ) を通過 ( + ) もしくは反射 ( - ) するパターンは次に示すように、16種類 (= 24) ある。
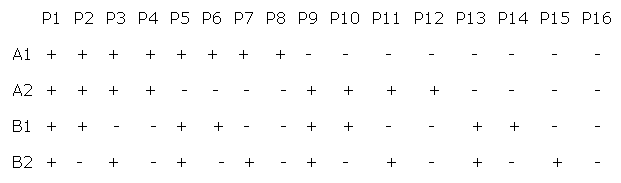
ここで、このパターンすべての確率の和は1になる ( P1 + P2 + P3 + ..... + P15 + P16 = 1 )。
また、つぎのように定義する。
---------------------------------------------------------------------
< A1, B1 > = ( A1とB1の符号が同じ確率、 + + と - - ) - ( A1とB1の符号が違う確率、 + - と - + )
= (P1+P2+P5+P6+P11+P12+P15+P16) - (P3+P4+P7+P8+P9+P10+P13+P14)
同じように、
< A2, B1 > = ( A2とB1の符号が同じ確率、 + + と - - ) - ( A2とB1の符号が違う確率、 + - と - + )
= (P1+P2+P7+P8+P9+P10+P15+P16) - (P3+P4+P5+P6+P11+P12+P13+P14)
< A2, B2 > = ( A2とB2の符号が同じ確率、 + + と - - ) - ( A2とB2の符号が違う確率、 + - と - + ) = (P1+P3+P6+P8+P9+P11+P14+P16) - (P2+P4+P5+P7+P10+P12+P13+P15)
< A1, B2 > = ( A1とB2の符号が同じ確率、 + + と - - ) - ( A1とB2の符号が違う確率、 + - と - + )
= (P1+P3+P5+P7+P10+P12+P14+P16) - (P2+P4+P6+P8+P9+P11+P13+P15)
---------------------------------------------------------------------
すると、次の等式にたどりつく。
< A1, B1 > + < A2, B1 > + < A2, B2 > - < A1, B2 > = 2 ( K - L )
K = P1+P2+P6+P8+P9+P11+P15+P16
L = P3+P4+P5+P7+P10+P12+P13+P14
(K + L) = Σ Pi = 1 の関係式を用いると、
-1 = - (K + L) ≦ (K - L) ≦ (K + L) = 1 の関係式が成り立つ。
すると、次の不等式 ( ベルの不等式、CHSH型 ) が成り立たないといけない。
| < A1, B1 > + < A2, B1 > + < A2, B2 > - < A1, B2 > | = 2 | K - L | ≦ 2
例えば、光子A (→ A1) と光子B (→ B1) の結果が同じ ( + + と - - )になる確率は、cos2 (A1-B1) である。。
ここで、(A1-B1) はフィルターA1とB1の間の角度差である。 (= Fig.20 の θ にあたる。)
光子AとB両方とも フィルターで反射する確率も cos2 (A1-B1) に関係する。
光子Aが フィルターAで反射したとき、光子Bの偏光軸は フィルターAに垂直になる。
( これはつまり、光子BとフィルターBの間の角度が π/2 - (A1-B1) になることを意味する。)
そのため、光子B が フィルターBを反射する確率は sin2 π/2 -(A1-B1) = cos2 (A1-B1) となる。
( 正確には、( + + ) と ( - - ) の合計が cos2 (A1-B1) となる。つまり ( + + ) と ( - - ) のそれぞれは その 半分である。)
また、これの結果が別に ( + - と - + ) になる確率は、sin2 (A1-B1) である。
つまり、 < A1, B1 > は、
(Eq.1)
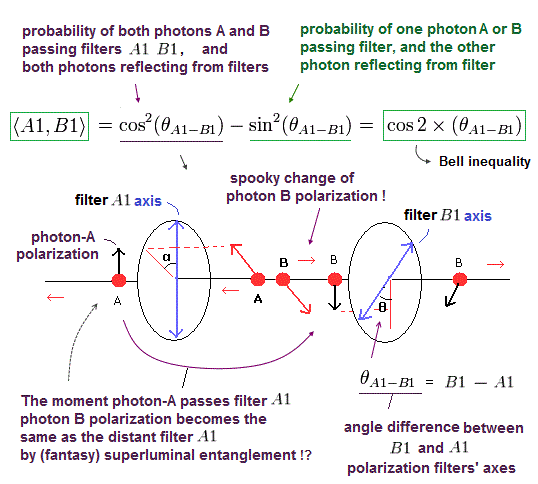
ここで θA1 - B1 は 角度 (A1 -B1) と同じ意味である。
Fig.28 の場合では、各 cosine の値は次のようになる。
(Eq.2)
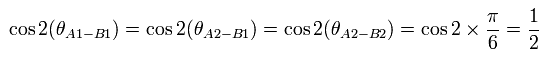
と
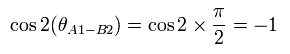
Eq.2 より、上のベルの不等式 (CHSH 型) は、
(Eq.3)
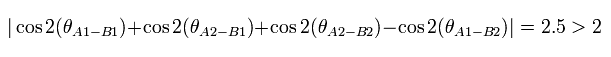
これはベルの不等式を破っている!
結論として、もし、一つの光子が分離できない粒子であるとしたら、エンタングルメントという奇妙な非局所的な現象は実際に起こっており、この現象を信じなければならない。
言いかえれば、もし、光子が分離可能な電磁波ならば、この光速以上の伝達を許すファンタジーを考慮する必要がないということだ。
どちらが(光子が粒子か波か)より自然な話か 判断は簡単である。
ベリリウムイオン (Be+ ion) ( もしくは、ytterbium Yb+ ion )のときはどうだろう? ( ion trap qubits と呼ばれる 。)
このとき、パウルトラップ(Paul (ion) trap) という極めて外的な電場、磁場の環境下でイオンがトラップされた状態でのみ、もつれた状態になる。これは光子のケースと比較してかなり人工的、人為的な環境といえる。
Be+ イオン間の距離は 数 µm と非常に短いため 局所性ループホールが存在する。
よって、このトラップの調整しだいで、いくらベルの不等式が破れたからといって、イオン対のもつれという幻想を引き起こしている可能性は極めて高いといえる。
(このページも参照のこと。)
なぜなら 彼らの現在のスタンスでは "リアル"な科学の発展が妨げられているからである。

まず最初に 量子もつれなどの研究者や ニュース編集者は 単に "量子もつれ" という魅惑的な言葉だけで 一般人を惑わすだけでなく、彼らが 実験手順をよく理解できるように伝えるよう 努力すべきである。
3体問題であるヘリウムに関連した時間のギャップのために あるトップジャーナルが 量子もつれや 量子コンピューターなどの架空の分野を広めてしまったことは ある意味避けられないことである。
( そうなった経緯は 十分理解できるし やむを得ない。 )。
しかし 幻想を これからも永久に追及することは すなわち 私たちが 非現実性と "Shut up and calculate !" の姿勢を 永久に認めることになり ここで科学が ずっと止まってしまう。
[ ベルの不等式の破れは 今だに幻想のままである。 ]

あるトップジャーナルで、 すべての局所実在性のループホールが閉じられたというニュースを見たりする。
しかし 注意してみると それらの実験は すべてのループホールを同時に閉じているわけではなく、かつ 通常の CHSH のベルの不等式でなく 低検出効率を許してしまう 特殊な不等式を用いている。
この 特殊な不等式の実験結果には 検出効率のすべてのデータが示されていない。
つまり 通常の CHSH の不等式の 約半分のデータ量から ループホールの有無を判断してしまっている。
彼らの光子対検出効率の定義 (= 同時検出 / どちらか一方のみ検出 ) を用いれば、上記の電磁波モデルは 優に 検出効率が 100 % を越えてしまい 簡単に古典的な立場で説明できてしまう。
[ 3つのすべてのループホールは 公式にも "同時" には閉じれらていない。]

上記の特殊な不等式を用いた実験では 3つあるループホールのうち、
"fair-sampling" というループホールを単独で閉じたことになっているにすぎない。
( この fair-sampling loophole は 今まで ただ一つ閉じられていなかったらしい。 )
"検出効率"、 "局所性"、 "fair-sampling" の3つのループホールは 同時には 公式的にも 閉じられていないのである。
( そのため これら3つの抜け穴を同時に閉じることを今も 彼らは目指しているわけである。)
(Fig.T-1) "1" と "4" 光子は 本当に 異なった時刻でも "もつれ"ているのか?

最近のニュースでは"もつれた"光子は 同時に存在しなくてもいい という実験結果がでた というのが目に飛び込んできた。
しかし この種の量子もつれの実験結果のトリックは 上で何度も述べたとおり、彼らが 必ず "電磁波" でなく "光子" というワードを用いているところにある。
Fig,T-1 では、もつれた光子対 (= 1, 2 ) が 最初の BBO という部分で生成されている。
( そのうち1つは 水平偏光 (= H )、 もう1つは 垂直偏光 (= V) である。 )
光子1の状態を検出した後、別の光子対 (= 3, 4 ) が生成される。
それから 光子 2 と 3 を混ぜて、その後 2 と 3 の光子の偏光状態 (= H もしくは V ) を検出する。
もちろん、それらはミックスされているため、どっちが 上下の検出器に入ったかは分からない。
(Fig.T-2) もつれた "光子対" が本当に生成された ?

もつれた光子対は しばしば "パラメトリック下方変換" によって BBO の部分で生成される。
この過程では 波長 λ の光子が ある結晶に入射すると、波長 2λ のペアの光子対に分離する。
そのため 全エネルギーは保存する (= それらの振動数は半分になる )。
しかし 何度も言うようだが、光子が粒子だとしたら、そんなに簡単に それを分離することはできない。
生成された光子対の1つは 水平偏光、もう1つは垂直偏光である。
ということは 明らかに これらは 古典的な電磁波で 粒子ではない。
どうやって 点状粒子の光子が 偏光することができるのだろうか?
どう考えても不可能である。
(Fig.T-3) パターン I 光子対 ( 2, 3 ) = ( V, V ) → ( 1, 4 ) = ( H, H ).

"2" と "3" の両光子とも 垂直偏光 (= V ) の光子として検出したとき、 1 と 4 の光子は 共に 自動的に 水平偏光の光子 (= H ) ということになる。
これは 当り前の結果である。なぜなら 最初に BBO で 1つは H、もう1つは V の光子対を生成したからである。
そのため 彼らは 光子対 1 と 4 が ミステリアスな "もつれた"状態であると主張しているのである。
しかし あなた方も感じられたように、これらの結果は 通常の古典的な電磁波の視点からすれば しごく当たり前の結果である。
それでは なぜ 彼らは これらの状態が 超光速のエンタングルメントであると主張しているのだろうか?
(Fig.T-4) 彼らは "仮想の" 古典的な光子対を仮定している。

これらの結果が どうしてミステリアスな量子もつれ状態なのか おそらく一般の方々は よく分かっていないと思われる。
上で述べたように、この種の実験は いわゆる "古典的な光子" というものを想定している。
もし この古典的な光子というものが実在すれば、それらは ビームスプリッターで分離されず、たとえ それらの偏光状態が同じでも、必ずしも同じ偏光結果を与えない。
例えば、 Fig.T-4 では フィルター A と B が 同じ方向を向いている。
( また 光子 A と B の両方とも 同じ偏光状態である。)
もつれた光子対では、1つの光子がフィルターを通過したとき、不気味なリンクによって もう1つの光子も 必ずフィルターを通過する。
しかし 古典的な光子では、光子 A が フィルター A と通過しても、光子 B は 必ずしも フィルター B を通過しない。
( Fig.T-4 に示したように、sin2 α の確率で反射する。)
これらの詳しい説明は 上のセクションで述べてある。
(Fig.T-5) 両方の電磁波が ( ++ ) 検出できるほど十分に通過した。

もし 古典的な"光子" が 単なる幻想であるとし、通常の古典的な"電磁波" の概念を用いると、この種の実験を 局所実在的な視点から 容易に説明することができる。
最初に、"2" と "3" の光子を検出器で検出できたとき、それは ビームスプリッターを通過した "2" と "3" の両光子ともに "光子" として検出されるだけの十分な光の強さがあったことを意味している。
( もし それらの光の強さが 弱いとき、検出閾値以下のため、それを単一光子として検出できず、無視される。)
つまり このケースでは "1" と "4" の両方の光子も それぞれ指定の偏光方向に 光子として検出されるだけの十分強い光度を持つことになる (= このケースでは H と H )。
例えば、光子 "2" を "V" 偏光として検出できたとしたら、それはすなわち 光子 2 は ビームスプリッターに入る前から おおよそ "V" の方向を向いていたということを意味している。
なぜなら もし 光子 2 が "V" と "H" の中間の方向 (= 45°) を向いていたとしたら、それは 通過側と 反射側に ほぼ半分に分割されて ( cos2 45 = sin2 45 = 1/2 ) 検出閾値に到達できない。
(Fig.T-6) パターン II.

光子 2 と 3 を 1つが "V", もう1つが "H" 偏光として検出したとき、1 と 4 の光子でも 1つが "H"、もう1つが "V" ということになる。
これもまた 通常の古典力学的な視点からみても 当然の結果と言える。
"ベル測定" というのは 両光子とも 検出する必要がある。
つまり 2 と 3 の光子のうち 1つしか 検出できなかったときは、それらの結果は もちろん実験結果として採用されない。 (= ここにトリックがある。)
量子もつれの研究者達には申し訳ないが もし一般の方々に 超自然的な概念を広めようとするならば、最低限 どういう実験手順をしたかということを 一般人に詳しく説明して 納得させる ( "信じさせる" でなく ) 義務があると思われる。
例えば、2つの電子がもつれて(エンタングルメントして)スピンゼロの状態 (spin up + spin down = spin 0) になっているとき、磁気モーメントは打ち消されてゼロになると一般には言われている。しかし本当にそうだろうか?
答えは、NO である。なぜなら、2つの電子はクーロン反発力でお互いに離れており、仮に反対の磁気モーメントを持つ2つの電子が完全にくっついて同じ場所に存在しないかぎり、その磁気モーメントの合計はゼロにならない。しかしそんなことは絶対に不可能だ。
[ 電子スピンに リアリティーはあるのか? ]
また、奇妙なことにスピンするフェルミ粒子(フェルミオン fermions) は一回転の回転では元の姿に戻らない。二回転させてはじめて元に戻る。
また、電子のスピンが電子の本当の自転によって生じるとしたならば、電子は軽くて、小さいため、そのスピン角運動量をだすには電子の表面のスピードが光速の100倍以上にならなければならない。
(このページも参照のこと。)
以上のことより、スピン(1/2)やエンタングルメントしてスピンのゼロ状態になるということは、単なるスピノル(spinor)によってしか表現できない。数学的な産物なのである(実体のある物理的産物ではない)。
また、元のスピン状態は 外磁場のもとでは、人為的にどうしても変わってしまう。
スピン1/2 の粒子ペアのエンタングルメントは 教科書に頻繁にでてくるが、実際の実験では 光子など別の粒子が使われる。
なぜなら、スピン1/2 粒子を使った実験は 非常に困難だからだ。
重要な点は スピン1/2 粒子の場合、ベルの不等式自体が 非現実的なものなのである。
これを今から説明していく。
最初に、極座標を使って、次の 単位ベクトル を定義する。
(Eq.4)

もし、スピンが この単位ベクトル方向を向いているとき、スピン演算子は次のように表せる。
(Eq.5)

これは、 n と S の内積である。
そのため、この n 方向で スピン +1/2 になる スピノル(= 固有関数 )は、
(Eq.6)

また、n 方向で スピン -1/2 になる スピノル は、
(Eq.7)

互いに反対のスピンをもつ 2つのスピン1/2 粒子が 正反対の方向に飛んでいると仮定する。
粒子Aのスピンを 測定Aで測定し、粒子B のスピンを 測定B で測定するとする。
最初に、この測定A が Eq.4 の単位ベクトル n の方向を向いていると仮定する。
もし、粒子Aが n 方向の測定Aで +1/2 と測定されたとき、エンタングルメントによれば、粒子Bが 瞬時に n 方向で - 1/2 の状態になる。
すなわち、粒子Aが Eq.6 の α の状態になった瞬間に、粒子B は Eq.7 の β の状態になることを意味する。
次に、測定B の方向を z 方向と仮定する。
(そのため、測定AとBの間の角度は θ となる。)
Eq.7 によれば、粒子Bのスピンが z 方向で -1/2 になる確率は
(Eq.8)

粒子Aが 測定Aで +1/2 となり、粒子Bが 測定Bで -1/2 となるとき、このケースを " ( + + ) " と名付けることにする。
なぜなら、それらのスピンは互いに 反対方向の状態が普通だからである。
また、粒子Bのスピンが z 方向の測定で +1/2 になる確率は、
(Eq.9)

粒子Aが 測定Aで +1/2 で、粒子Bが 測定Bで +1/2 のとき、このケースを " ( + - ) " と名付けることにする。
同様に、粒子Aが 測定Aで -1/2 のとき、粒子Aは Eq.7 の β になり、粒子Bは 瞬時に Eq.6 の α になる。
つまり、粒子Bのスピンが z 方向で +1/2 になる確率は、
(Eq.10)

粒子Aが 測定Aで -1/2 となり、粒子Bが 測定Bで +1/2 となるとき、この場合を " ( - - ) " と名付ける。
また、粒子Bのスピンが z 方向で -1/2 になる確率は
(Eq.11)

粒子Aが 測定Aで -1/2 で、粒子Bが 測定Bで -1/2 のとき、このケースを " ( - + ) " と名付ける。
つまり、上の光子の場合のように、( + + ) と ( - - ) の確率 − ( + - ) と ( - + ) の確率は、
(Eq.12)

ここで、 θA1-B1 は、測定A1 と B1 の間の角度を意味する。
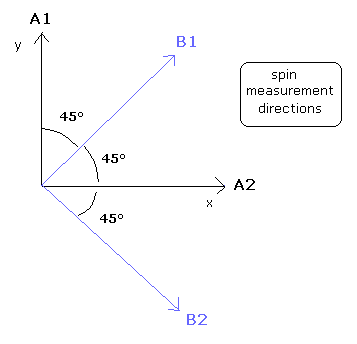
そこで、次の4つの測定 (各粒子につき2つ) をする。(Fig.29)
(Fig.29) 粒子A → 測定 A1 と A2。 粒子B → B1 と B2。
すると、各 cosine の値は、次のように計算される。( Eq.12 のように )
(Eq.13)

と

この場合の スピン 1/2 の粒子の ベルの不等式は
(Eq.14)

これは ベルの不等式を破っている !
しかし、もう一度 Eq.6 と Eq.7 に戻ってみよう。
Eq.6 と Eq.7 によれば、スピノルは なんと一回転で元に戻らないのだ!
( それは 元に戻るのに 2回転必要なのである。 )
つまり、スピノルというものは、現実の物体ではないのである。
すなわち、スピン1/2 粒子の場合は、Eq.14 の ベルの不等式そのものが 間違いなのである。
結論として、スピン1/2のエンタングルメントを実際の現場で考えるという発想そのものが無理があり、幻想である。
( エンタングルメントという幻想は、光子 や スピン1/2粒子 という "非現実の"粒子によって生じたものなのである。)
多世界解釈 (many-worlds interpretaion MWI) は最初にエヴェレット (Hugh Everett) によって提唱された [5]。
そして今や多世界解釈は量子力学的解釈 (the quantum mechanics QM) の中で最も優れていると考えられている。
しかし、私も含めて多くの人々は多世界なんて単なる空想のファンタジーだと思っている。
多世界では、重なった(superposition) 波束(波動関数)の収縮 (collapse of the wavefunctions) は、量子デコヒーレンス (quantum decoherence) によって説明できるとしている。
このデコヒーレンスによって量子力学のEPRパラドックスや、シュレディンガーの猫 (Shroedinger's cat) の問題を解決できるとしている。
( しかし、この デコヒーレンス とは、非常に都合のいい解釈で、ある程度物体が大きくなると、干渉がなくなるというものだ。意図的な解釈すぎると思わないだろうか? )
また、コペンハーゲン (Copenhagen) 解釈に見られる、観測者による波束の収縮(observer triggered collapse) などは考えなくてよいことになっている。
(確かに、観測者だけを 特別視して 波束の収束を引き起こさせることは 不自然極まりない。)
(Fig.30) すべての解釈は不自然である。 → "Shut up and Calculate !"

もっとも現実を重視した解釈がド・ブロイ-ボーム解釈 (De Broglie-Bohm or Bohmian mechanics) であろう。
しかし、この解釈では奇妙なことに、電子に電荷とスピンがないことになっている。
なぜなら、電子に電荷があったとしたら、シュレデインガー波動関数の確率密度分布に従って複雑に運動している間に加速度運動でエネルギーを放出していってしまうからだ。
(よって、クーロン力 (Coulomb force) もないことになる。)
また、この解釈では波束の収縮で電子がときには光速を越える(タキオン)にもなり得るとしている。
それによく考えてみよう。例えば単純な水素原子の波動関数の基底状態でさえ、無限遠近くの確率密度は完全に0にならない。こんなバカげた話があるだろうか?
一方でボーア模型では、単純な円もしくは楕円軌道の長さがちょうどド・ブロイ波長の整数倍のとき、電子運動が安定し、エネルギーを放出しないとしている。きわめて妥当なモデルといえる。
ここで、登場するのが、初期モデル "コペンハーゲン解釈" ( Copenhagen interpretation ) である。
さきほど述べたとおり、観測者だけを特別扱いする矛盾を含んではいるが、基本的な姿勢は "Shut up and Calculate !" (それ以上つっこまず、黙って計算だけしてろ!) なのである。
多世界やら ボーム解釈などの 他のどの解釈も 不自然で かつ問題をかかえているため、結局は 物理学者達は、量子力学を数式のみの世界とあきらめて、結果だけを追及することにしている。
つまり、量子力学は現実をあらわすことが不可能なのである。
(量子力学をあきらめなければ、不自然な解釈をなくすことは不可能である。これはすなわち ボーア模型のみが real な 模型として残ることを意味する。)
もっと重要な問題は これらすべての解釈はどれも 相対論的場の量子力学 (the relativistic quantum field theory) と矛盾していることだ。
これらすべての解釈は非因果的で確率振幅を表すシュレディンガー方程式を基礎に成り立っている。
しかし非相対論的量子力学(nonrelativistic QM) では、微細構造(スピン軌道相互作用)を含む相対論的効果を表せない。
一般に、重い原子になればなるほど、核の電荷が強くなり、内殻の電子の速度が光速に近づき、相対論的エネルギー補正が必要になってくる。
これによってシュレディンガー方程式の解と現実のエネルギーとの違いが顕著になってくる。
つまり、もともと不完全な方程式なのだ。
また、シュレディンガー方程式では核の電荷にかかわらず、いかなる電子も電子雲として静止しているとして、エネルギーの放射を防いでいるとしている。
一方、ディラック方程式 (Dirac equation) は相対論的因果律を満たし(いかなるものも光速をこえない)、また相対論的効果を正確に計算できる。
だが、デイラック方程式には確率密度分布という概念がないのだ。
つまり、実際のイメージはできず単なる数学的な産物なのだ。
ようするに量子力学は相対論的量子力学と非相対論的量子力学という自己矛盾を含んだ理論なのだ。
自己矛盾は残念ながら、その時点でアウトだ。
最後に、ボーア・ゾンマーフェルト理論 (Bohr-Sommerfeld theory)はどうだろうか?
ゾンマーフェルトはボーア模型を相対論的効果も正確に計算できるモデルに発展させた。
偶然にもこの解は水素原子のデイラック方程式の解と完全に一致する。
これはデイラック方程式がスピン軌道相互作用と電子速度による相対論的効果を互いに相殺させるという人工的かつ不自然な操作を何回もしているからだ。
確率的にもこんなに一致するのはおかしい。
一方、ゾンマーフェルドのほうは、スピン自体がないため、自然に微細構造などの実験結果を再現できる。
もちろん、ボーア模型は自己矛盾は何も含んでいない。 詳しくはトップページを参照のこと。
[1] A. Einstein, B. Podolsky, N. Rosen: "Can quantum-mechanical description of physical reality be considered complete?" Phys. Rev. 41, 777 (1935).
[2] J. Bell: "On the problem of hidden variables in quantum mechanics" Reviews of Modern Physics 38 #3, 447 (1966).
[3] A. Aspect, Dalibard, Roger: "Experimental test of Bell's inequalities using time-varying analyzers" Phys. Rev. Letters 49 #25, 1804 (1982).
[4] A. Aspect, P. Grangier, G. Roger: "Experimental realization of Einstein-Podolsky-Rosen-Bohm gedanken experiment; a new violation of Bell's inequalities" Phys. Rev. Letters 49 #2, 91 (1982).
[5] Hugh Everett: "Relative State Formulation of Quantum Mechanics" Reviews of Modern Physics 29 454 (1957).

2010/2/15 updated This site is link free.