
トップページ (正確な新ボーア模型)
電子スピンは存在しない。
微細構造の導出。
(Fig.1) スピン軌道相互作用は 間違った概念である。

ここ、 ここ、 ここ にあるように、ナトリウムの D 線は 相対論的効果の一種である スピン・軌道相互作用によって 生じるとされている。
しかし このページに示したように、スピン・軌道相互作用は Na、K などのアルカリ金属の実際のデータを説明するには 弱すぎる。
このことは、スピン・軌道相互作用という概念自体が 幻想であることの証である。
(Fig.2) ディラック水素 = ボーア・ゾンマーフェルト模型。

このサイト や このサイト (p.12) にあるように、ボーア・ゾンマーフェルト模型は ディラックの水素と まったく 同じ微細構造のエネルギー値を与える。
このページ (= ディラックの水素 ) と このページ (= ゾンマーフェルト ) を比較するといい。
この偶然の一致は 非常に不自然極まりないものである。
もちろん、ゾンマーフェルト模型が ディラック方程式よりも 前に 登場していることから、後者が 前者の解を 模倣したことは 一目瞭然である。
ディラックの水素原子解に関しては このサイト (p.9) や このサイト (最後の式) を参照のこと。
(Fig.3) 同一の微細構造の近似解。.

ここ (p.135)、 ここ (p.9)、 ここ (p.13)にあるように、微細構造の近似解として Z4/n3 に比例する式を得ることができる。
"Z" は 有効中心電荷で、これは 原子核と他の 内殻のすべての電子の電荷の総計である。
"n" は 主量子数で、主要なエネルギー準位を表す。
このセクションで、元のディラック (= ゾンマーフェルト ) の水素原子解から この近似式を導出した。
(Fig.4)

例えば、水素原子の 2p3/2 と 2p1/2 の準位間のエネルギー差を求めるとする。
両方の模型で 主量子数 "n" は "2" である。
全角運動量は 2p3/2 で j = 3/2、 2p1/2 で j = 1/2 である。
ボーア・ゾンマーフェルト模型では、動径量子数 nr = 0 (1)、 角運動量数nφ = 2 (1) が それぞれ 2p3/2 (2p1/2) に相当する。
(Fig.5) ↓ この公式も同じ結果を与える。

近似的に 微細構造の式として Fig.4 の解の代わりに Fig.5 の式を使える。
Fig.5 に l = 1 ( ディラック形式における角運動量 ) を代入すると、この式は 2p3/2 と 2p1/2 のエネルギー準位間の微細構造を与えることになる。
もちろん、ボーア・ゾンマーフェルト模型も Fig.5 と完全に 同じ式を与えることは言うまでもない。
ボーア模型には スピン という概念がないにも関わらず、まったく同じ式になるということは 単なる偶然と片付けるには 余りにも無理がある。
(Fig.6) 水素の微細構造。

このサイトにあるように 水素原子における 2p3/2 と 2p1/2 準位間のエネルギー差は 約 0.000045 eV である。
この値は非常に小さいため、スピン磁気モーメント (= また偶然にも ボーア磁子と同じ ) というのが 重要な物理現象に ほとんど関与していないことが理解できる。
(Fig.7) エネルギーの単位変換。
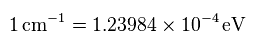
水素原子のエネルギー準位は Nistに載っているが エネルギーの単位として eV の代わりに cm-1 を用いている。
このサイトを用いて 任意の値を cm-1 から eV (= エレクトロンボルト ) に変換できる。
(Fig.8) Nist の水素のエネルギー値。

Nist にある 水素の 2p3/2 と 2p1/2 のエネルギー値より、 eV に変換して Fig.8 の値を得る。
よって、これら2つの準位間のエネルギー差は、
(Fig.9)

このエネルギー差を 微細構造と呼び、Fig.6 の結果と同じである。
このセクションに示したように、このエネルギー差 (= ΔE ) は Fig.10 のシンプルな式で表わすことができる。
(Fig.10) 微細構造。

このページでは、Fig.10 の式が 様々な原子やイオンにおいても 必ず成り立つのかどうか 実際に調べることにする。
(Fig.11) H と He+ における微細構造。

このサイトを見ると、電子を1つ失った ヘリウムイオン (= He+ ) の 2p3/2 と 2p1/2 の準位間のエネルギー差が 0.00072 eV であることが分かる。
(Fig.12) 中心電荷 Z。

Fig.12 にあるように、 H と He+ における 中心の正電荷は それぞれ Z = 1 と Z = 2 である。
(Fig.13) 各微細構造の計算。

Fig.10 の公式を用いると 水素とヘリウムイオンの両方で この公式が成り立つことが分かる。
なぜなら He+ のエネルギー差 (= 0.00072 eV ) は 水素 (= 0.000045 eV ) の 16 倍 ほど大きいからである。
この 16 という値は Z = 2 を Z4 に代入したときの 値に等しい。
このセクションで、 JAVA サンプルプログラム を用いて 実際に計算して 式の妥当性を確認できる。
(Fig.14) Li と Be+ の微細構造。

このサイト と このサイトから、 リチウムとベリリウムイオンにおける 2p3/2 と 2p1/2 の準位間のエネルギー差を得ることができる。
(Fig.15) Li と Be+ の 中心電荷は H と He+ に近い。

もちろん、リチウム原子の 中心の有効電荷は Z = 1 に近くなる必要がある。
なぜなら この中心電荷 Z は 原子核と内殻のすべての電子群の電荷を含んでいるからである。
同様に、Be+ の中心電荷は He+ のように Z = 2 に近くならなければならない。
(Fig.16) 微細構造公式は Li と Be+ においても有効。

Fig.10 (= Fig.3 ) の公式と プログラム による計算値より、この微細構造の式が リチウムとベリリウムイオンにおいても ほぼ成り立つことが示せる。
(Fig.17) ナトリウムの D 線は 単一電子スピンで説明するには 大きすぎ。
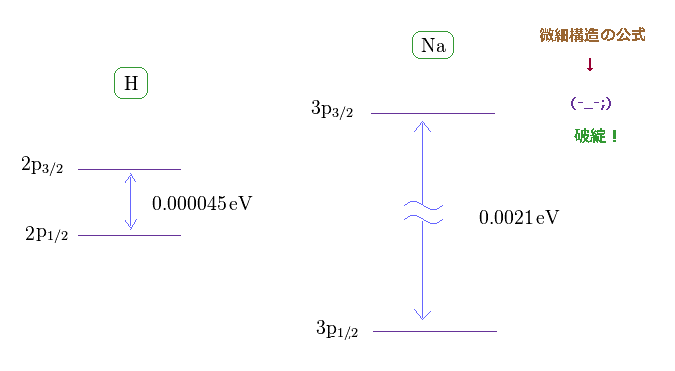
このサイトにあるように、水素の 2p3/2 と 2p1/2 準位間の 微細構造 (= 2重項 ) は 約 0.000045 eV である。
一方で、ナトリウムの 3p3/2 と 3p1/2 準位間の 微細構造は 0.0021 eV もある。 このサイトも参照のこと。
近似的に、ナトリウムの 3p ( もしくは 3s ) 準位の電子は Z = +1 の中心の芯の部分の電荷の周囲を 回っていると見なせる。
( "芯の部分" とは Na の原子核と n=1 と n=2 の軌道に含まれる すべての電子の合計の電荷の意味である。 )
この外殻電子からの視点では、中心の芯電荷は 逆方向に回っており、スピンを持つ電子の部分に 磁場を生じさせることになる。
結果的に スピン・軌道相互作用が生じると彼らは主張している。
(Fig.18) Na の中心の有効電荷は Z = 1 よりもはるかに大きい Z = 3.54 !?

水素とナトリウムの外殻電子 (= 3p ) の両方において、それらが感じる 芯部分の有効電荷は
約 Z = +1e ぐらいになると考えるのが自然である。
しかし これらの H と Na のスピン軌道相互作用間の違いは あまりにも大きい。
これはつまり ナトリウムにおける 有効中心電荷は Z = 1 よりも はるかに大きくなければならない ( Na で Z = 3.54 ぐらいになってしまう )。
この結果は 現実のナトリウム原子の観点からして あまりにも非現実的で 不合理である。
(Fig.19) スピン軌道相互作用が正しいと 有効芯電荷 "Z" が 大きくなりすぎてしまう (= 3.5 )。

3p の価電子が感じる 中心の有効電荷は ナトリウム (= Na ) においても Z = 1 に近くなる必要がある。
しかし Z = 1 のとき、スピン軌道相互作用のエネルギーの計算結果は 小さくなりすぎて、とても 0.0021 eV の実験値には届かない。
Z = 3.54 のとき、微細構造公式は この 0.0021 eV の実験値をだすことができる。
この結果は 実際の微細構造において、スピン軌道相互作用というものが 起きていないことを 示している。
(Fig.20) イオン化エネルギーから 本当の有効芯電荷が Z = 1.84 であることが分かる。

このサイトから、Na の イオン化エネルギーが 5.14 eV ( n = 3 ) であることが分かる。
この値と 水素 (= 13.606 eV、 n = 1 ) の値を比較することで、Na の 本当の有効芯電荷量が Z = 1.84 であることが分かる。
この 1 より少し大きい Z は n = 2 の内殻の電子群の間に 大きなギャップが存在していて 価電子に 核の影響が漏れていることを示している。
と言っても もちろん Z = 3.54 には 到底 届かない。
(Fig.21) Na と Mg+ における 大きな微細構造ギャップ。

このサイト (= Na ) と このサイト (= Mg+ ) から、 Na と Mg+ (= 1つの電子を除いたもの ) の 3p1/2 と 3p3/2 準位間のエネルギー差を知ることができる。
(Fig.22) 有効芯電荷 Z が Na と Mg+ で大きくなりすぎる。

Fig.21 と 微細構造の公式より、Na と Mg+ の有効芯電荷量が 非現実なくらい 大きくなりすぎることが分かる。
Na と Mg+ の Z は それぞれ 3.54 と 5.39 になり、 1 (= H ) と 2 (= He+ ) よりも はるかに大きい。
(Fig.23) 非現実的な 有効芯電荷 Z。

すでに述べたように、この有効芯電荷 Z は 原子核と すべての内殻の電子群 を含んでいる。
そのため、 Na と Mg+ の Z は "1" と "2" に近づく必要がある。
この結果は スピン軌道相互作用の概念自体が 様々な金属において 破綻していることを示している。
このページに示したように、もっと大きな原子 K, Cs .., では さらに この有効中心電荷の量の 非現実性が 増大する。
(Fig.24) n = 1 よりも n = 2 の電子殻のギャップが はるかに大きい。

n = 2 の平均軌道半径は n = 1 よりもはるかに大きい。
( 原子半径は n の 2乗 に比例する。 )
つまり Na における n = 3 の価電子は n = 2 の電子殻における 大きなギャプを通じて 水素やリチウムよりも 強力な クーロン力を 感じることになる。
内殻の電子群の広い隙間こそが 金属における 大きな微細構造の主要な原因である。
つまり ( 架空の ) スピン軌道相互作用ではなく クーロン力による影響を考えなければならない。
(Fig.25) 軌道形 (= 楕円 や 円形 ) の違いが 大きな微細構造の原因。

このページに示したように、ボーア・ゾンマーフェルト模型の微細構造は 楕円形 と 円形軌道という 軌道形の違いによって生じる。
水素においては 両者の平均の軌道半径は同じである。
しかし 楕円軌道では その近日点が 円形軌道に比べて はるかに 原子核に 近づくことになり、これが クーロン相互作用の違いを引き起こす。
(Fig.26) スピン軌道模型では 大きなクーロン作用の違いは 起こせない。
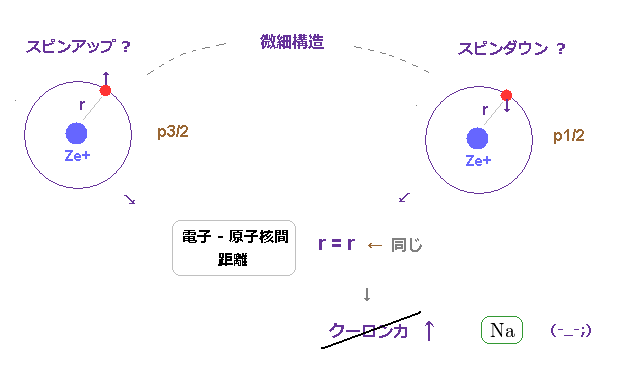
一方で、この微細構造が スピン軌道相互作用によって生じるとすると、これら2つの状態は
同一の 軌道形 ( 例えば 3p ) を持つことになる。
同一の軌道形では クーロン相互作用において 何の違いも
起こさない。
つまり スピン軌道相互作用模型では 金属における大きな微細構造を まったく説明できない ことになる。
結果的に ボーア・ゾンマーフェルト模型の方の微細構造が 正しい結果を与え得る唯一のものとして 残ったことになる。
(Fig.27) 計算式1 -- Fine structure by original equation (= ディラック、ゾンマーフェルト )

このセクションでは、 この JAVA プログラムを用いて、Fig.27 と Fig.28 の2つの式を計算する。
このプログラムを "finest.java" という名で コンパイルする。
(Fig.28) 計算式2 -- Fine structure by Z^4/n^3 form。

最初に 水素の微細構造 (= 2p3/2 と 2p1/2 の準位間のエネルギー差 ) を計算する。
このプログラムを実行後、 "1" (= Z ) を入力し、エンターキーを押す。
この Z は 中心電荷の意味である。
次に "2" (= n ) を 主量子数として入力し、エンターキーを押す。 .
最後に "1" を入力する。これは j=3/2 (= p3/2 ) と j=1/2 (= p1/2 ) 間のエネルギー準位差を計算するという意味である。
(Fig.29) 各値の入力。水素原子の微細構造の場合。

計算結果は Fig.30 のようになる。
"finestructure by original equation" の右にでた値は Fig.27 の計算式によって出した結果である。
"finestructure by Z^4/n^3 form" の横の値は Fig.28 の式を用いて出した結果である。
(Fig.30) 計算結果。

Fig.30 の結果にあるように、 Fig.27 と Fig.28 の公式は 同じ計算結果を与える。
つまり Z4/n3 を含む近似的な式が 正しいことを表している。
(Fig.31) He+ イオン の場合。

He+ イオンでは、最初の質問で、Z = 1 の代わりに Z = 2 を入力する。
このケースでも、 Fig.27 と Fig.28 が 同じ結果を与えることが分かる。
(Fig.32)

(Eq.1) ディラックの水素 = ボーア・ゾンマーフェルト模型。

このサイト や このサイト (p.12) にあるように、ボーア・ゾンマーフェルト模型は ディラックの水素と まったく 同じ微細構造のエネルギー値を与える。
このページ (= ディラックの水素 ) と このページ (= ゾンマーフェルト ) を比較するといい。
この偶然の一致は 非常に不自然極まりないものである。
ディラックの水素原子解に関しては このサイト (p.9) や このサイト (最後の式) を参照のこと。
(Eq.1) 同一の微細構造の近似解。.

ここ (p.135)、 ここ (p.9)、 ここ (p.13)にあるように、微細構造の近似解として Z4/n3 に比例する式を得ることができる。
"Z" は 有効中心電荷で、これは 原子核と他の 内殻のすべての電子の電荷の総計である。
"n" は 主量子数で、主要なエネルギー準位を表す。
(Eq.3)

Eq.2 の分母の一部を "A" に置き換える。
もちろん、ゾンマーフェルトとディラックの両方の模型で共通の値である。
(Eq.4) ゾンマーフェルトとディラック形式の変換。

ボーア・ゾンマーフェルト模型では、主量子数 "n" は 動径方向 (= nr ) と 接線方向 (= nφ ) の量子数の和になる。
ディラック方程式では、全角運動量として 共通の変数 "j" を用いている。
この "j" は 軌道 (= "l") と スピン (= s ) 角運動量の和である。
そのため、2つの状態が 異なった軌道角運動量を持っているとしても、それらの "j" が同じとき、エネルギー準位は 同じになる。
(Eq.5) 全エネルギー

Eq.3 の "A" を用いて、Eq.2 のエネルギー準位は Eq.5 のように表せる。
ここで、この式に Eq.6 のテイラー展開を適用する。
(Eq.6) テイラー展開。
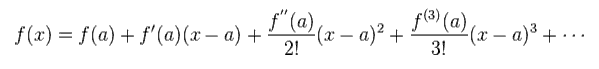
ここでは
(Eq.7)

Eq.7 から、Eq.5 の全エネルギー E は 次のようになる。
(Eq.8)

Eq.3 と 微細構造定数 α が小さいことによる近似を用いると、次を得る。
(Eq.9)

ここでは 次を使う。
(Eq.10)
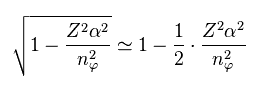
Eq.9 から、次を得る。
(Eq.11)

さらに、微細構造定数 α が 非常に小さい (= 1/137 ) ことより 次の近似を使用できる。
(Eq.12)

Eq.11 と Eq.12 を Eq.8 に代入して、全エネルギー E は 次のようになる。
(Eq.13)

主量子数 "n" が 共通の値の時、角量子数 (= nφ ) のみ エネルギー値に影響を与える。
そのため Eq.13 の3項目の nφ を含む項のみをピックアップする。
(Eq.14)

Eq.14 にあるように、この値は Z4/n3 に比例している。
ここで 角運動量が1つ違うエネルギー準位間の差を求める。
すなわち 共通の "n" で、角量子数が nφ と nφ+1 の場合である。
(Eq.15)

Eq.4 に示したように、これら2つの状態は ディラック形式の 異なった"j" に相当する。
"l" は 軌道角運動量である。
(Eq.16) 共通の "n" における 2つの準位間のエネルギー差 (= 微細構造 )

Eq.14 と Eq.16 から、2つの状態のエネルギー差が Z4/n3 に比例することが分かる。
これら2つの状態は 同じ主量子数 "n" に存在し、 全角運動量 "j" ( or nφ ) が 1つのみ異なる場合に相当する。

2014/8/17 updated This site is link free.