トップページ (2電子原子も含む正確な新ボーア模型)
場の量子論の終焉。
電子スピンは幻想である。
QED のラムシフトは間違い。 (13/11/3)
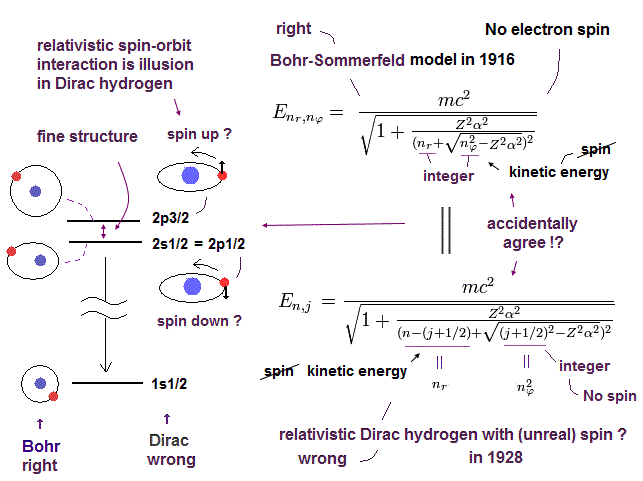
(Fig.1) 偶然の一致?

あなたがたは ボーア模型は 水素原子の微細構造などについて説明できないと しばしば聞いたことがあるかもしれない。
しかし このページで示したように、有名な微細構造は 1916 年にボーア・ゾンマーフェルト模型によって最初に得られたものなのである。
現在公式に認められている微細構造は ディラックによる水素原子である。
驚くことに、ディラック方程式によるこれらの解は ゾンマーフェルト模型の解と きっかり一致しているのである。
ほとんどの方は この事実をご存じないだろう。
Fig.1 では、 nr と nφ は 動径方向と接線方向のゾンマーフェルトの量子数であり、これは このページに示したように 各方向の ドブロイ波長 を表している。
( ボーア模型では、1軌道は ドブロイ波長の整数倍である。)
ディラックのほうの "n" と "j" は、エネルギー準位と全スピン角運動量 ( j = l + s ) を意味している。
(Fig.2) ゾンマーフェルトとディラックによる微細構造。
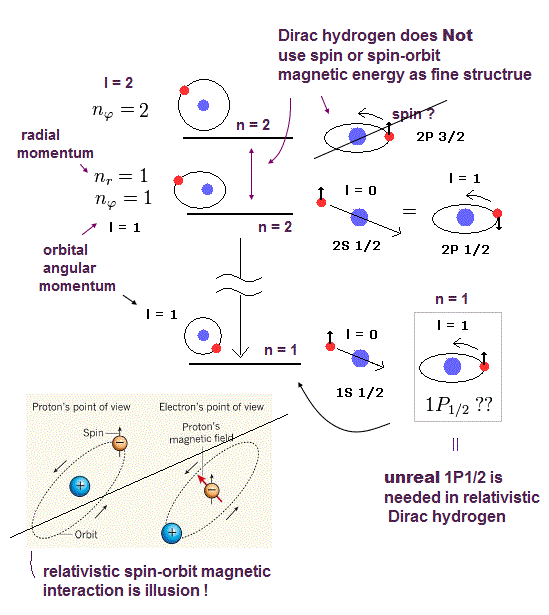
Fig 2 は エネルギー準位 "2" 内の エネルギー差を示している。
このページに示したように、ゾンマーフェルト模型は ボーアの円軌道を 楕円軌道に拡張した。
円軌道は 接線方向の動きしか含まず、楕円軌道は動径方向の動きも含む。
相対論効果 (= 最高速度 "c" ) を考慮すると、これらの 2つの軌道は エネルギーレベルでわずかに分離している (= 微細構造 )。
一方で、ディラックの水素原子は 3種類の状態を エネルギー準位 "2" 内に含んでいる ( 2s1/2、2p1/2、2p3/2 )。
しかし 実際のスペクトル線は 2本の分離しか認められない。
(Fig.3) ディラック = ゾンマーフェルト !?

Fig.3 の上は ゾンマーフェルトの楕円軌道 ( nr = 1、 nφ = 1 ) のエネルギー準位を表している。
驚くことに Fig.3 下に示すように、 ディラックの 2s1/2 と 2p1/2 の状態は ゾンマーフェルトの楕円軌道と 完全に一致するのである。これらの根源はまったく異なるものなのにである。
( ディラックの水素原子は "スピン"の効果を含み、ゾンマーフェルトのほうは含んでいない。)
"n = 2" は エネルギー準位 = 2、 "j = 1/2" は 全角運動量 = 1/2 の意味である。
ディラック 2s1/2 は 軌道角運動量がゼロだが、スピン角運動量 1/2 を持つため、 j = 0 + 1/2 = 1/2 となる。
一方、 2p1/2 は 軌道角運動量 ( l = 1 ) で かつスピンを持つため、 j = 1 - 1/2 = 1/2 となる。
結果的に これらはエネルギー準位でまったく同じになる。これはちょっとできすぎてないだろうか?
(Fig.4) ディラック = ゾンマーフェルト !?
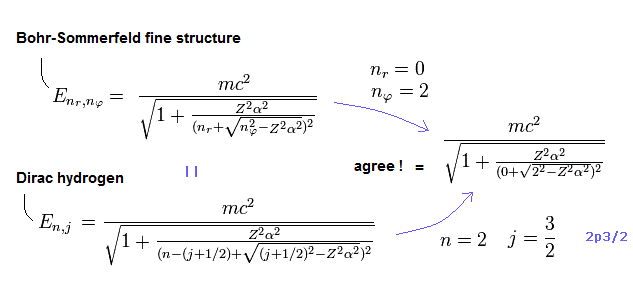
Fig.4 の上は ゾンマーフェルトの 円 軌道 ( nφ = 2, nr = 0 ) である。
( 円軌道とは 動径方向の運動を含まないという意味である。 )
Fig.4 の下は ディラックの水素の 2p3/2 状態であり、全角運動量は j = 1 + 1/2 = 3/2 である。
ディラックの水素原子の エネルギー準位 "2" の最高の軌道角運動量は l = 1 ( p 状態 ) であり、j = 3/2 が n = 2 におけるマックスとなる。
驚くことに、これらの模型のエネルギー準位は完全に一致するのである。ゾンマーフェルト模型のほうには
スピンが含まれていないにも関わらずだ。
(Fig.4') 偶然の一致の連続。
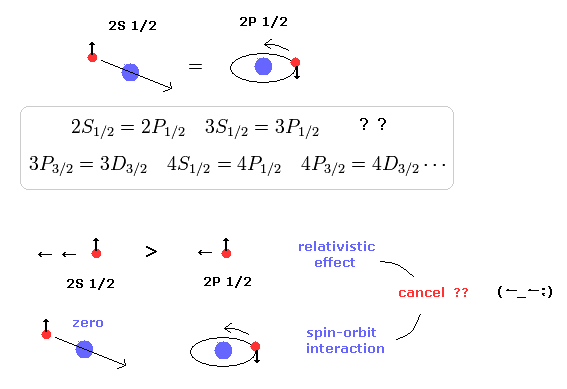
Fig.1 と Fig.3 に示したように、2つの異なった状態 ( 2s1/2 と 2p1/2 ) が 共通の全角運動量 j を持つとき、それらのエネルギー準位は 互いに完全に一致する。
2s1/2 の状態は ゼロの角運動量であるため、2p1/2 の状態のみ スピン・軌道相互作用 が存在する。
2s1/2 のほうが 核に近づけるため、相対論的質量が重くなり 2s1/2 のエネルギー準位が 2p1/2 よりも少し低くなる。
驚くことに、この相対論的質量の違いが 2p1/2 のスピン軌道相互作用によって ちょうどキャンセルされてしまうのである。
結果的に エネルギー準位は 2s1/2 と 2p1/2 で ちょうど等しくなるということであるが、あなたがたは ちょっとできすぎた話だと思われないだろうか?
さらに、ディラックの水素原子は 他にも たくさんの偶然の一致を含んでいるのである ( 3s1/2 = 3p1/2, 3p3/2 = 3d3/2, 4s1/2=4p1/2 ..... ) 。
この奇妙な状態を信じることができるだろうか?
これらの偶然の一致は 明らかに 彼らが ボーア・ゾンマーフェルトの微細構造と同じ解を得ることを 目指して こしらえたものである。
(Fig.5) ディラック方程式の起源。

このページに示したように、ディラック方程式は 相対論的なエネルギーと運動量の関係式から 作られたものである。
クライン・ゴルドン方程式が 最初に 特殊相対論から得られたが 2次式だった。
そのため その1次式を 得ることを目指して ディラック方程式に至ったわけである。
1次式になった引き換えに、ディラック方程式は 4 × 4 γ 行列と スピノルを含まなければならなかった。
(Fig.6) スピノルは エネルギー準位の縮退?

後で説明するが、ディラックのハミルトニアンは 軌道角運動量演算子と交換しないので ディラックの水素原子解は 2つ以上の角運動量を含む必要がある。
そこで 彼らは 4 × 1 のスピノルを利用して 2s1/2 と 2p1/2 のような 縮退を表そうとしたわけである。
( 例えば、上部2成分のスピノルは 2p1/2、下部2成分は 2s1/2 である。)
結果的に、ディラックの水素原子は 実験結果や ボーア・ゾンマーフェルトの水素と 一致することができた。
しかし このタイプの波動関数は オリジナルのディラック方程式には使用されておらず、水素原子に特異的な形式である。
つまり、これらの特殊な関数の形式は ゾンマーフェルト模型と同じ解を得るために 導入されたといっていい。
(Fig.7) 副作用? = ディラックの水素原子の実在しない状態
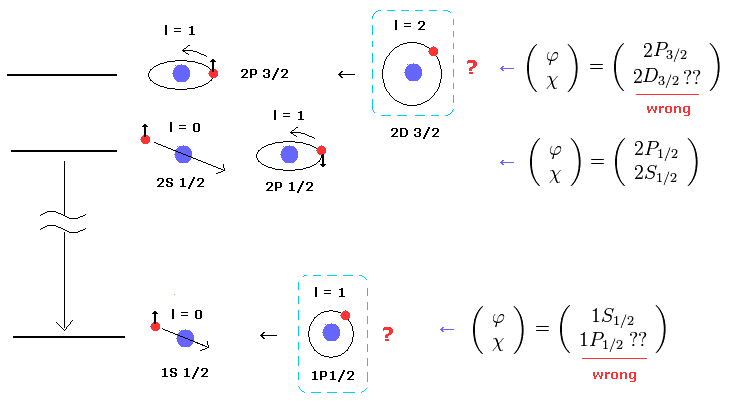
しかし この副作用が現れた。
2s1/2 と 2p1/2 のケースはいいが、2p3/2 のケースでは その正しいペアを持つことができない。
2p3/2 は n = 2 のエネルギー準位で、全角運動量は j = 3/2 である。
上記のロジックによれば、2p3/2 のペアは 非実在の 2d3/2 になる必要がある。
これは l = 2 の軌道角運動量を持つため、量子力学の水素原子には存在しないものである。
なぜなら シュレディンガーの水素原子は n = 2 に 角運動量 "2" の準位は存在しないからである。
後で説明するが、これらの矛盾は 明らかに ディラックの水素原子が 間違いであることを示している。
ディラックの水素原子は これらの間違った状態 (= 1p1/2、2d3/2、3f5/2 ... ) をたくさん含んでいるのである。
もし、ディラックの水素原子が間違っているとしたら、私達は 非常に小さなラムシフトの解釈を変更する必要がある。
なぜなら ラムシフトは ディラックの水素原子が正しいという前提条件に完全に依存しているからである。
( このページも参照のこと。 )
(Fig.8) ラムシフトの解釈。

水素原子のラムシフトは 非常に小さく (= 0.0000043 eV ) 微細構造の約 10分の1 ほどである。 ( 核スピンの超微細構造ぐらいである。)
非常に小さなラムシフトは 通常のスペクトル線で観察することはできない。
彼らは この非常に小さなラムシフトを 2s1/2 が 準安定で かつ 励起した水素原子とプレートを衝突させる方法が ラムシフトの分解能を十分有すると 信じて、測定しようとした。
この実験では 少し修正した異常ゼーマン効果が 常に線形に成り立っていることや 準安定状態が 本当に 2s1/2 なのかという 保証がない。
このページに示したように、これらは単なる仮定にすぎない。
もちろん、衝突させる方法は ラフで この非常に正確な値の測定には不向きである。
最新の分光学的手法でも これらの状態が 本当に 2s1/2 と 2p1/2 の違いを表しているのか 確認することはできない。
ラムシフトが 核スピンの超微細構造ほどの大きさであることを考慮すれば、核もしくは電子のわずかな振動などが この小さな結果に影響を与えている可能性がある。
(Fig.9) ディラックの水素のエネルギー。

このページでは、自由粒子のディラックのハミルトニアン (= エネルギー ) を得た。
ディラックの水素原子では、クーロンポテンシャルを このハミルトニアンに追加した (= Fig.9 )。
もちろん ハミルトニアンの γ 行列は 4×4 行列であり、これらは 上下部のスピノルをミックスさせて 連立方程式を作り、これを解くことになる。
(Fig.10) エネルギー解を得るための連立方程式。

これらの意味は後で説明する。
ハミルトニアンは 運動エネルギー、静止エネルギー (= mc2 )、クーロンポテンシャルエネルギー (= V ) から成り立っている。
通常のシュレデインガー方程式のように、運動エネルギーを 動径方向と 接線方向に分離する。
もちろん、解のほうも 動径、接線部分に分離する。
(Fig.11) 接線方向の部分。
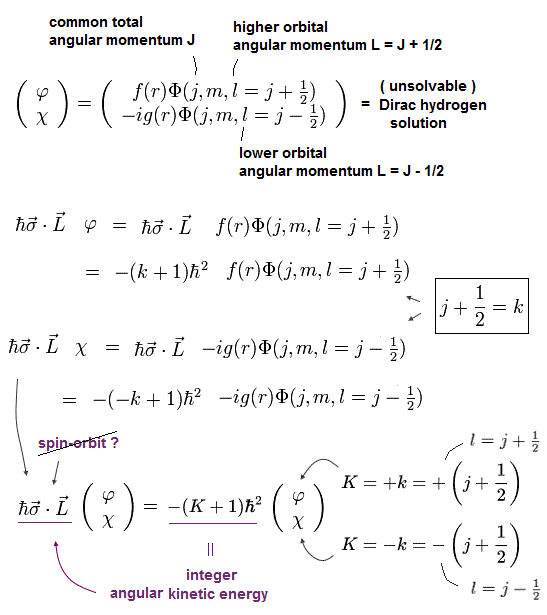
上下部のスピノルは Fig.6 に示したように 異なった角運動量を持つ。
"接線方向"の運動エネルギー演算子は 波動関数の角の部分に作用する。
後で説明するが、この演算子が 軌道角運動量 l = j ± 1/2 を見分けることになる。
もし 上部のスピノルが 角運動量 l = j + 1/2 を持つとしたら、下部の角運動量は l = j - 1/2 になる。
そして これらは 共通の全角運動量 j を持つため、この違いは Fig.11 に示すように 共通の "k" によって表される。
結果的にディラック方程式は 多くの 間違った状態を含むことになる。 例えば、 1p1/2 (= 1s1/2 のペア )、 2d3/2 (= 2p3/2 のペア )。
これはつまり、ディラックの水素原子は間違いで、1916 年の ボーア・ゾンマーフェルトの微細構造が正しいことを意味している。
(Fig.12) 動径の波動関数。

このページに示したように、シュレディンガーの水素原子の 動径方向の波動関数 "rR" は 整数倍のドブロイ波長である。
ディラックの水素原子は 動径部分を得るのに、シュレディンガーの水素原子と同じ手法を用いている。
そのため 動径方向の波動関数は シュレディンガーの水素原子とほぼ同じになる。
しかし 下部のスピノルは 間違った架空の状態を含んでおり、通常のものとは異なっている。
問題は これらの間違った状態が ディラックの水素原子解を得るのに 必要不可欠だということである。
(Fig.13) エネルギー = 動径方向 + 角運動量。

通常のシュレデインガーの水素のときのように、動径方向の波動関数は そのままだと無限大に発散する。
この発散を止めるために、動径の多項式の係数が どこかでゼロになる必要がある。
この次数 " n' " と j を用いると、エネルギー準位 " n " が決定する。
そして ディラックの水素原子のこのエネルギー解は ボーア・ゾンマーフェルトの水素原子のとまったく等しくなる (= Fig.14 )。
これはちょっと出来すぎである。
(Fig.14) ボーア・ゾンマーフェルトの水素。

正確には Fig.9 のハミルトニアンは 相対論的に共変ではないということである。
なぜなら クーロンポテンシャルエネルギーは Fig.15 に示すように ローレンツ変換の下で 複雑に変化するからである。
(Fig.15) ディラックの水素原子 = 非相対論的。

これはつまり 本当の相対論的なディラックの水素原子は (もし存在するなら) Fig.13 のとは 異なったエネルギー解を与えることを意味している。
ラムシフトは 非常に小さいので、クーロンポテンシャルのこの形式が 陽子や電子のわずかな運動で 変化したら、その値も変化してしまう。
そのため Fig.13 に依存する ラムシフトの計算も 間違いということになる。
ディラック方程式は いろんな現象を説明することが知られている。
ディラックは 物理学と数学において天才的な才能の持ち主だった。
そのため 彼は パウリ行列と相対論を的確に結合させて 実験結果に合致することに成功した。
しかし 残念ながら ディラック方程式は ”具体的な物のイメージ”を示すことができない。
驚くことに 後に ディラック自身が 行列などの非可換性のものに 疑いの目を向け始めた。
( P.A.M. Dirac (1972) Relativity and quantum mechanics. Fields and Quanta Vol.3, 139-164. )
そして いつか 深いところで何か大きな変化が起こるのではと考えていた。
彼は 干渉のもととなる 波の位相 を最も重要なものと考えていた。
この事実は 非常に深遠で 意味のあることと思う。
おそらく 彼のいう”波”とは ドブロイ波のようなものを意味していたと想像できる。
場の量子論やディラック方程式の基本に関しては、このページを参照のこと。
最初に 行列に頼るディラック方程式は 非常に数学的な性質が強いことを気に留めておく必要がある。
このページ (Eq.5-1)に示したように、ディラック方程式は、
(Eq.1) ディラック方程式。

相対論的なエネルギーと運動量の関係式は 2次 ( p2 - E2/c2 + (mc)2 = 0. ) である。
相対論的な式に一致するためには、 γ 行列は次を満たす必要がある。
(Eq.2)
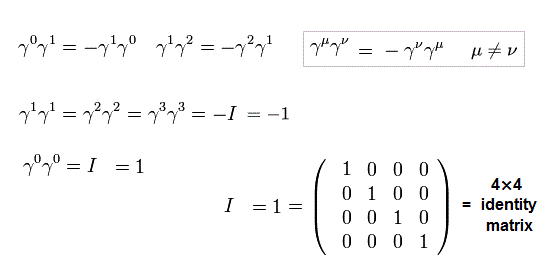
そのため、 Eq.2 を満たす γ0 行列は、
(Eq.3)
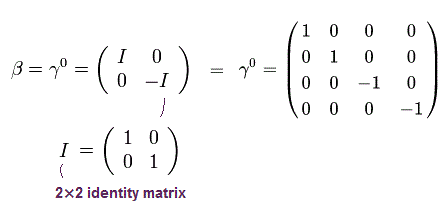
ここで I は 2 × 2 単位行列を意味している。
そのため、
(Eq.4)
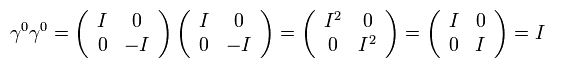
γ 行列の 1-3 の成分は、
(Eq.5)
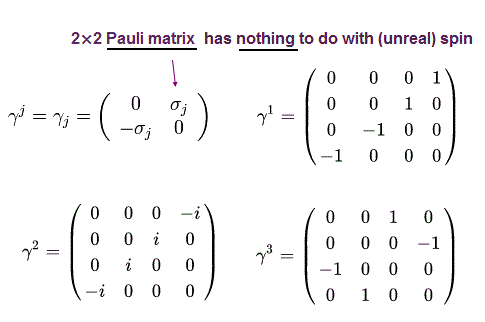
ここで j = 1, 2, 3
σj は 次の 2 × 2 パウリ行列である。
(Eq.6)
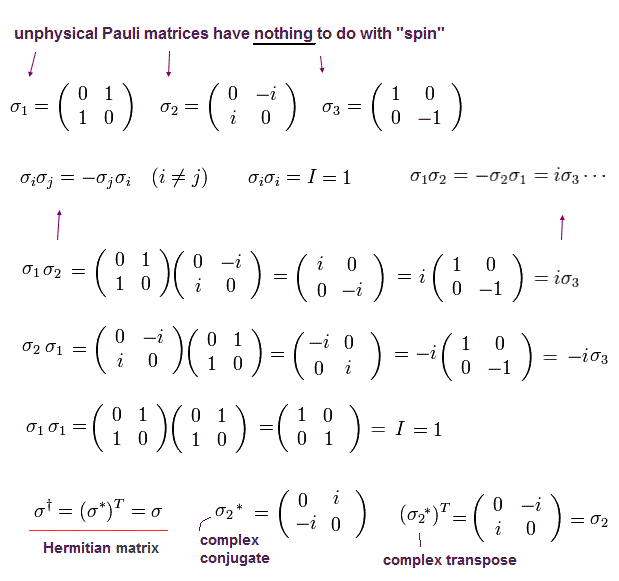
Eq.1 の左側から、 cγ0 をかけて、 γ0γ0 = I (= 単位行列 ) を用いると、次のディラックのハミルトニアンを得ることができる。
(Eq.7)

この結果は このページの Eq.5-39 と同じである。
Eq.3 の γ 行列と Eq.5 から、次を得る。
(Eq.8)
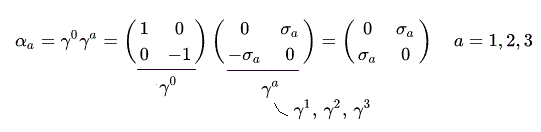
Eq.7 と Eq.8 から、クーロンポテンシャルエネルギー V を含む ディラックのハミルトニアン演算子 ( これは 全エネルギーを意味する。 ) は、
(Eq.9)

ここで p は 次に示すように 運動量演算子である。
(Eq.10)
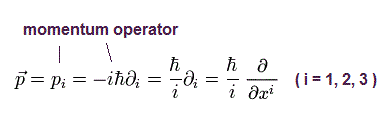
Eq.3、 Eq.5、Eq.8 を用いて、Eq.9 のハミルトニアンは、
(Eq.11)

ここで 波動関数 ψ を 2つの 2 × 1 行列に分離する。
(Eq.12)

後で説明するが、上下部のスピノルは 異なった角運動量を含まなければならない。
Eq.12 を Eq.11 に代入すると、 次を得る。
(Eq.13)

Eq.13 の上部は、
(Eq.14)

Eq.13 の下部は、
(Eq.15)

Eq.13 のポテンシャル V は 次の クーロンポテンシャルである。
(Eq.16)
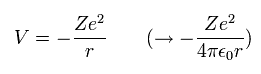
最初に 4πε を省いて、後で戻すとする。
そして Eq.14 と Eq.15 の連立方程式を解いて、水素原子のエネルギー解 E を得ることになる。
もちろん、Eq.14 と Eq.15 の エネルギー E は 共通の値である。
また 全角運動量 j も共通の値である。
しかし 軌道角運動量 "l" は 上下部のスピノルで 異なったものである。
結果的に ディラックの水素原子の波動関数は 次のような 多くの矛盾した状態を含んでいる。
(Eq.17)

1p1/2 は エネルギー準位が n = 1で 全角運動量が j = 1/2 であり、これは 1s1/2 状態とちょうど等しい。
しかし 1p1/2 状態は 非実在の l = 1 の角運動量を持つ。
なぜなら 1s1/2 の 軌道角運動量は l = j - 1/2 = 0 で、 1p1/2 のは l = j + 1/2 = 1 だからである。
もちろん、量子力学的な水素原子は エネルギー準位 n = 1 に 軌道角運動量 l = 1 を持ってはいけない。
つまり これは 自己矛盾である。
(Fig.16) 全角運動量 J と ハミルトニアン。
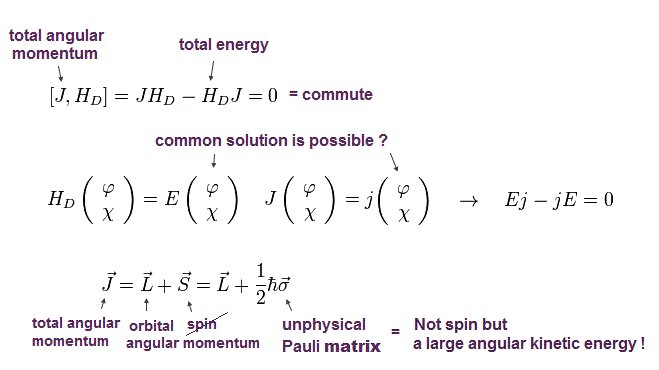
このセクションでは、全角運動量 J が ディラックのハミルトニアンと交換することを示し、これはつまり J と ハミルトニアンが 共通の固有関数を持つことを意味する。
なぜなら 共通の固有関数に作用する各演算子は それぞれの固有値を与え、それらは Fig.16 に示すように交換可能だからである。
(Fig.17) 軌道角運動量 L と ハミルトニアン。
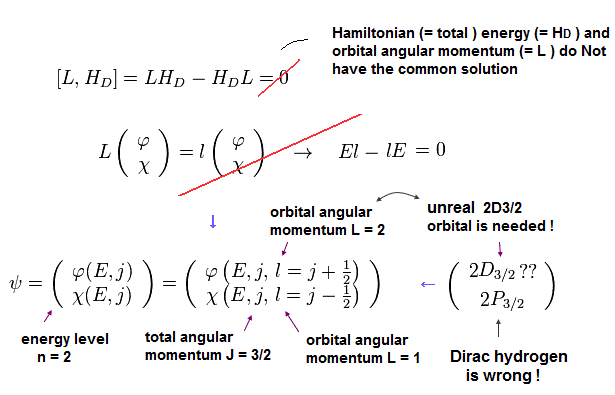
一方で、軌道角運動量 L は ハミルトニアンと交換しない。
これはつまり L と ハミルトニアンは 共通の固有関数を持てないことを意味する。
結果的に、例えば エネルギー準位 n = 2 で j = 3/2 の状態には l = j ± 1/2 の 異なった角運動量を含まなければならない。
もちろん 2p3/2 のペアである 2d3/2 は l = 2 であり、量子力学の水素原子には存在しないものである。
これらの事実は 明らかに ディラックの水素原子が 間違いであることを示している。
Eq.9 と Eq.11 から、 ハミルトニアンは、
(Eq.18)
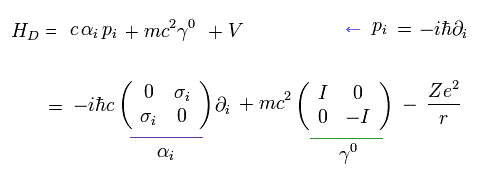
軌道角運動量 (L) は 次のように表せる。
(Eq.19)
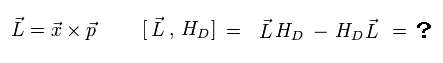
最初に この L の 3 (= z ) 成分について考える。
(Eq.20)
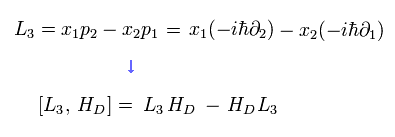
Eq.20 を用いて、この角運動量演算子 (L) が 次のように クーロンポテンシャル演算子 (V) と 交換することを示せる。
(Eq.21)
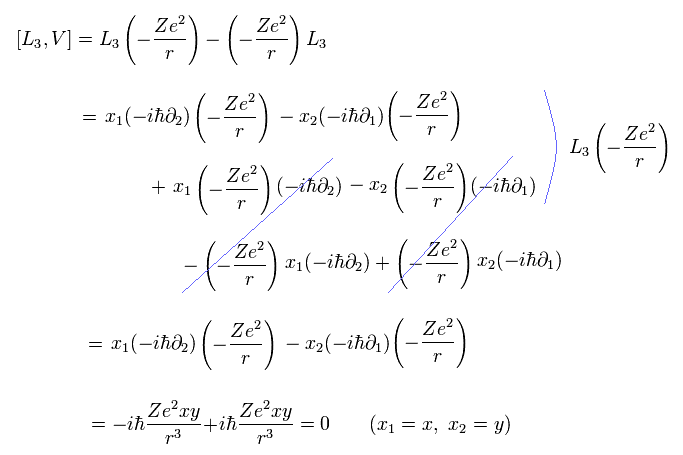
ここで 次の関係式を用いている。
(Eq.22)
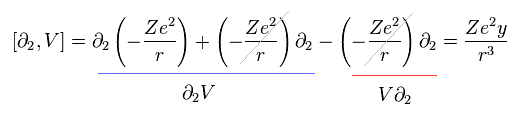
ここでは 運動量演算子は V の前後に作用する。
この角運動量 L は ディラックのハミルトニアンの 運動量 "p" と交換しない。
(Eq.23)
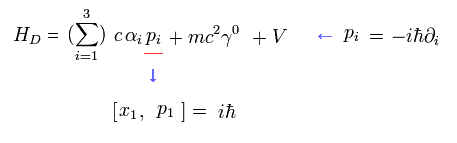
これは ドブロイの関係式である。
つまり、軌道角運動量 L と ハミルトニアンの交換は
(Eq.24)
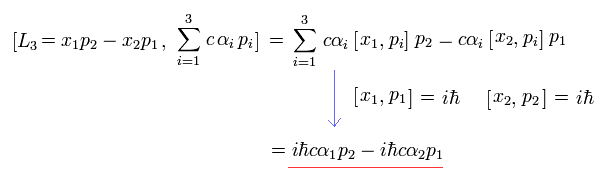
結果的に L と ハミルトニアンは交換しない。
次に スピン演算子 S について考える。
(Eq.25)
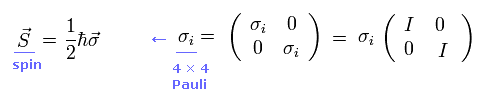
ここで σ は 4 × 4 の パウリ行列である。
このパウリ行列のスピンは ハミルトニアン内の Eq.8 の α の行列と交換しない。
(Eq.26)
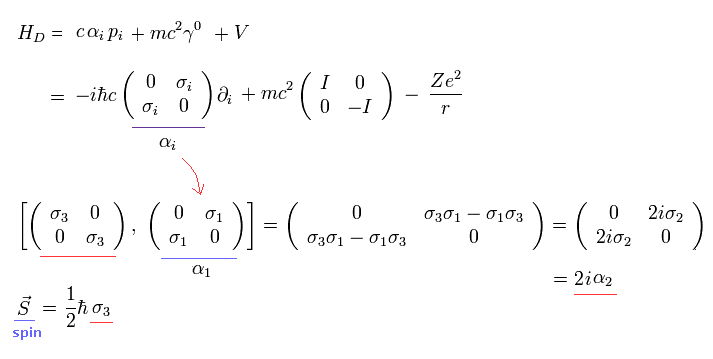
ここで Eq.20 の角運動量のように、スピンの 3 成分について考える。
この σ3 は、 ハミルトニアンの α1 と α2 と交換しない。
(Eq.27)
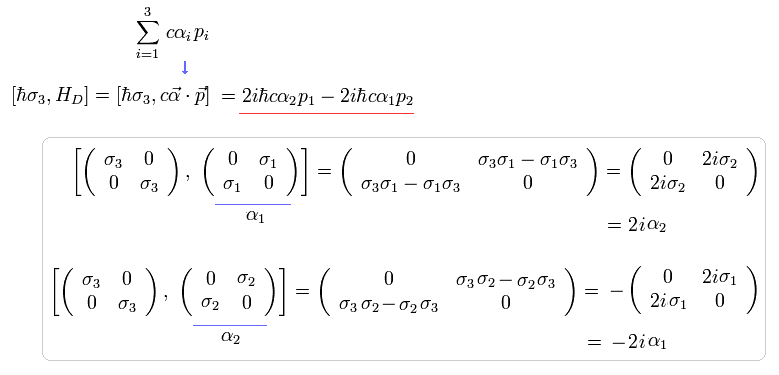
ここでは Eq.6 のパウリ行列の関係式を用いている。
全角運動量 (J) は 角運動量 (L) と スピン (S) 演算子の和である。
(Eq.28)
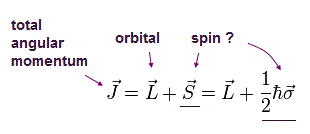
Eq.24 と Eq.27 から、 この J は ディラックのハミルトニアンと交換する。
(Eq.29)
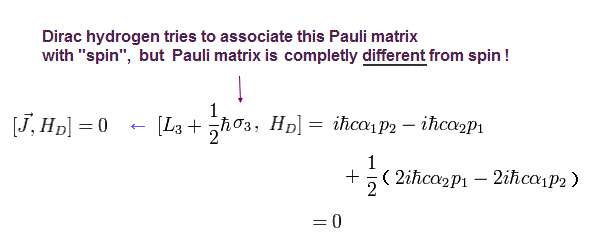
これはつまり、ディラックのハミルトニアンと J は 共通の固有関数を持てて、L と ハミルトニアンは 持てないということである。
結果的に、ディラックの波動関数は 必ず 同一の エネルギーと j で、 かつ異なった L を持つ ペア を持つ必要があるのである。
例えば、2p3/2 のペアは 架空の 2d3/2 になる。
Eq.28 より、全角運動量 (J) の2乗は、
(Eq.30)

ここでは パウリ行列の関係式 ( σσ = I ) を用いた。
Eq.30 の意味は、
(Eq.31)
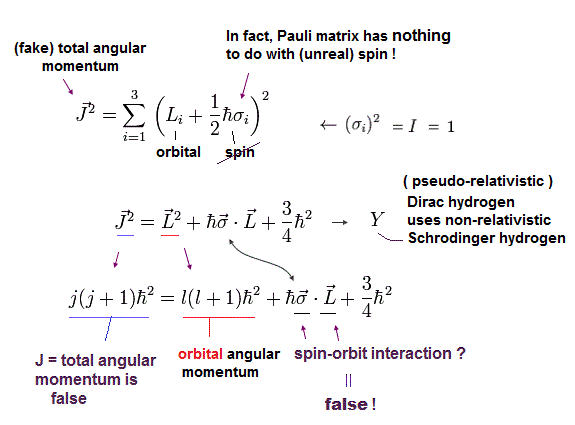
ここで J2 = j(j+1).
つまり l = j + 1/2 のとき、
(Eq.32)
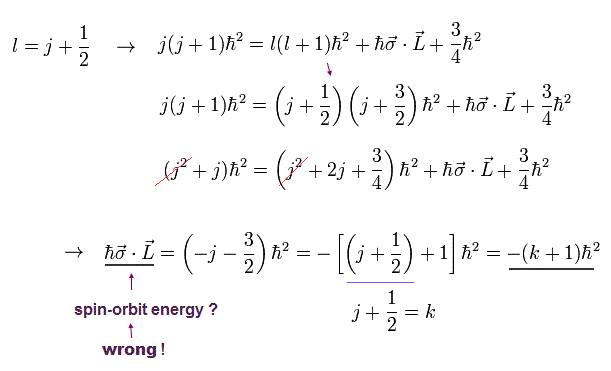
ここで k = j + 1/2 と定義する。
l = j - 1/2 のとき、 ( これを Eq.31 に代入して )
(Eq.33)
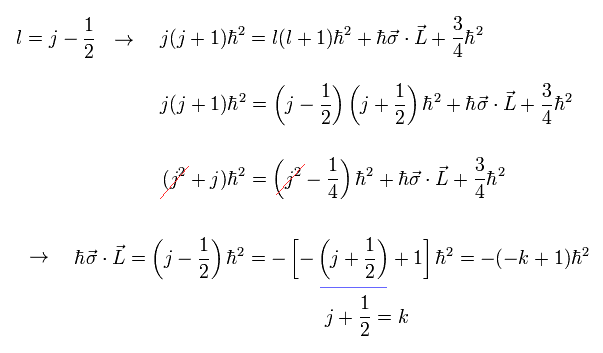
Eq.32 と Eq.33 に見られるように、 角運動量 L が異なると、k の符号は 逆になる。
( もし k が負になると、 Eq.32 と Eq.33 が 入れ替わる。 )
後で説明するが、ディラックの水素原子解を得るには、上下部のスピノルは 共通の J に関して 異なった L を持たなければならない。
ここでは Eq.32 と Eq.33 の連立方程式で 同一の "k" が使われている。
同一の "k" は 同一の "j" でかつ 異なった "L" の意味である。
つまり このディラックの水素原子は 1P1/2、2D3/2 などの多くの架空の状態を避けることができないのである。
なぜなら ディラック方程式は必ず 解を得るのに 上下部の 2成分のスピノルを 混ぜこぜにする必要があるからである。
Eq.29 と Fig.16 で述べたように、全角運動量 (J) と ディラックのハミルトニアンは 共通の固有関数を持つことができ、そのため ディラックのスピノルで たった1つの J の値を決定できる。
( 角運動量 (L) は ハミルトニアンと交換しないため、固有関数で 1つの L に決められない。)
(Eq.34)
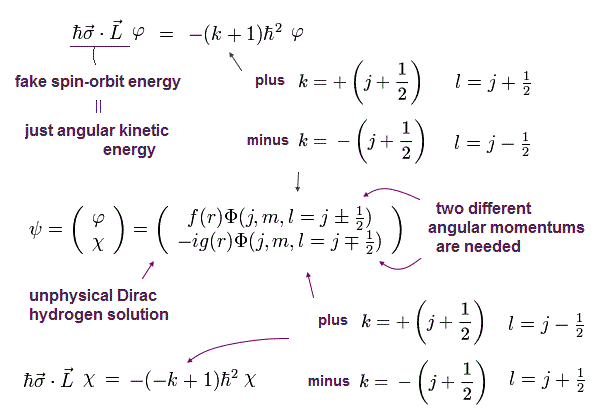
Eq.34 に示したように、固有関数は 2つ以上の異なった軌道角運動量 (= l ) を含まなければならない。なぜなら それはハミルトニアンと交換しないからである。
そのため 共通の j のもとでの 角運動量 (= l ) は l = j ± 1/2 になる必要がある。
例えば、上部の角運動量が l = j + 1/2 のとき、下部は l = j - 1/2 となる。
(Eq.35)
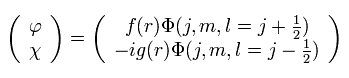
また 上部が l = j - 1/2 のとき、固有関数は、
(Eq.36)
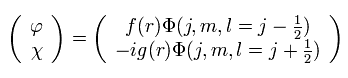
4成分のスピノルの上下部は 球面調和関数 (= Y ) を含む 2成分のスピノルから成る。
(Eq.37)
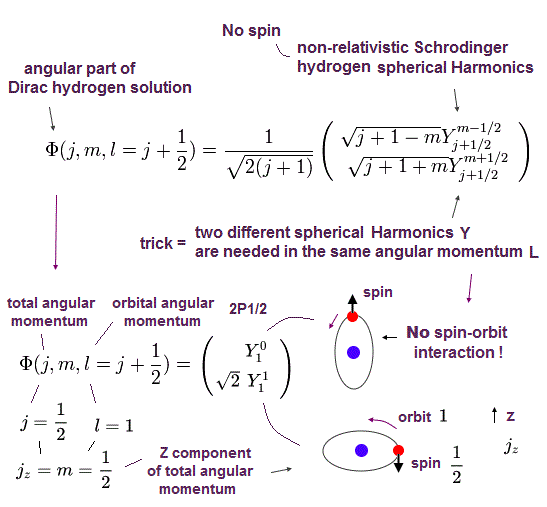
ここでは、 l = j + 1/2.
実際には これらの球面調和関数は計算で使用しないため、Eq.37、Eq.38 を単なるルールと考えておけばいい。
また l = j -1/2 のとき、
(Eq.38)
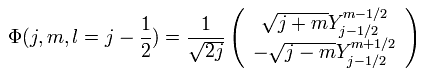
空間のパリティー演算子は 空間座標の反転を引き起こす。
空間反転のもとで、極座標は 次のように変化する。
(Eq.39)
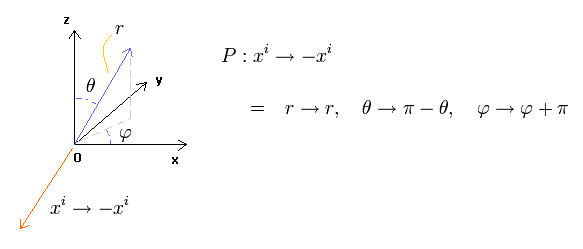
球面調和関数 (Y) は 空間反転のもとで 次のように変化することが知られている。
(Eq.40)
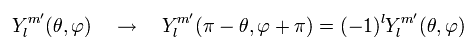
Y の角運動量 (= l ) が ± 1 変化すると、空間反転のもとで それは異なった性質を示す。
Eq.40 のいくつかの例をあげると、
(Eq.41)
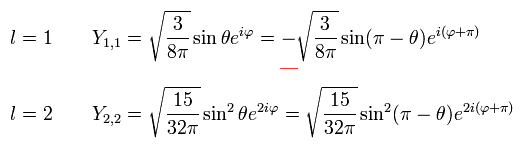
単位行列は 極座標を用いて 次のように表せる。
(Eq.42)

パウリ行列 (Eq.6) と 単位行列の内積は、
(Eq.43)
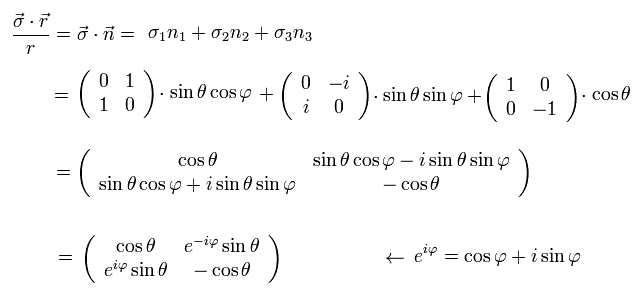
Eq.43 は 次を満たす。
(Eq.44)
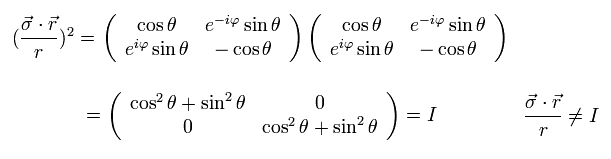
Eq.39 の空間反転のもとで、Eq.43 は次のように変化する。
(Eq.45)
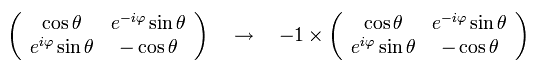
Eq.45 は Eq.43 の演算子が付加されると、空間反転のもとでの性質が
+1 → -1 (もしくは -1 → +1 ) と変化することを意味している。
つまり Eq.43 が球面調和関数 (Y) に付加されると、角運動量 (= l ) が 次のように ± 1 変化する。
( 動径部分 (r) は 変化しない。)
(Eq.46)
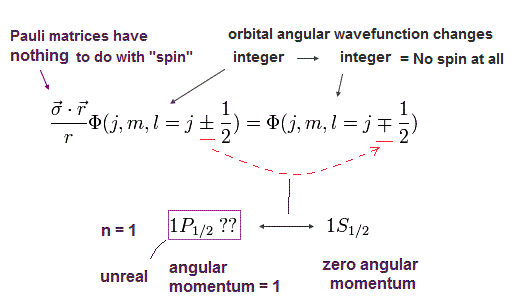
Eq.43 の演算子は 次のセクションで説明するが、ディラックのハミルトニアンに出てくる。
Eq.46 の結果は 少し想像することが難しいが、この関係式を用いないと ディラックの水素原子解を 得ることができない。
Eq.11 - Eq.16 に示したように、Eq.9 のディラックのハミルトニアンは 次のように表せる。
(Eq.47)

Eq.47 の上部は
(Eq.48)

Eq.47 の下部は、
(Eq.49)

パウリ行列 (= Eq.6 ) の関係式を用いると、
(Eq.6)
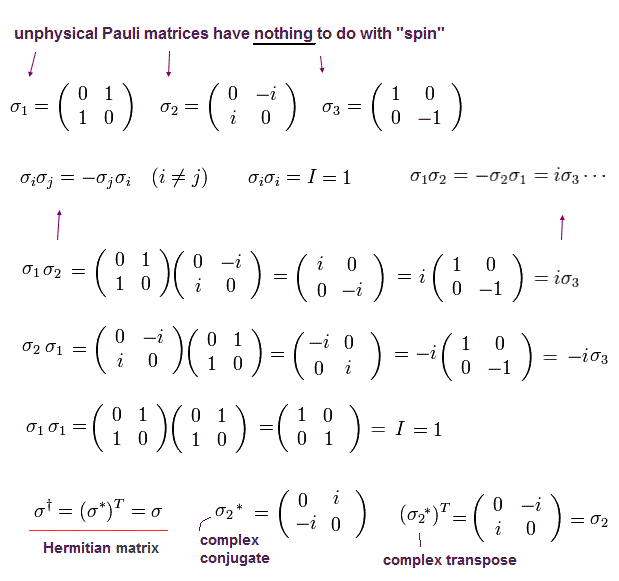
次を得る。
(Eq.50)
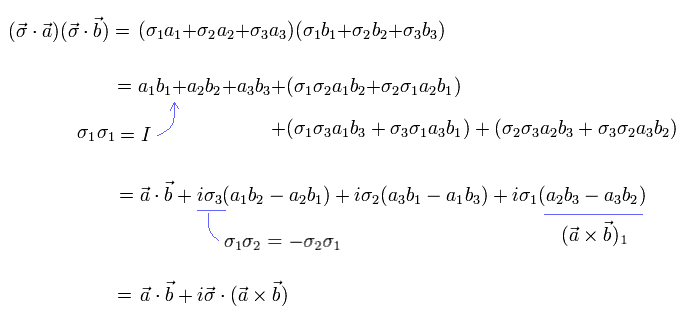
Eq.44 と Eq.50 を用いると、ハミルトニアンの運動エネルギー項 ( Eq.48 を参照 ) は、
(Eq.51)

Eq.43 の演算子がここで現れる。
Eq.32 より、次のように定義できる。
(Eq.52)

Eq.33 より、
(Eq.53)
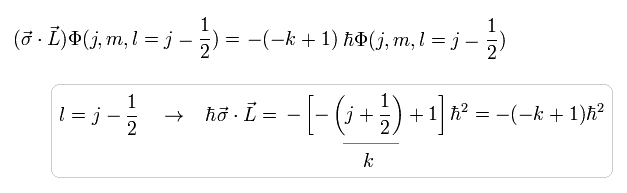
Eq.35、 Eq.51、 Eq.53 を用いると、Eq.48 の式は 次のように表せる。
(Eq.54)
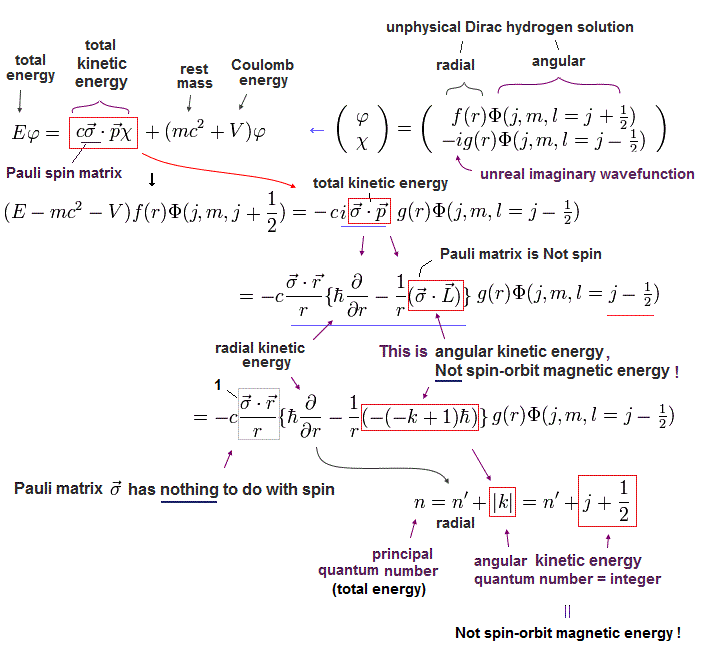
Eq.46 を用いると、
(Eq.46)

Eq.54 の球面調和関数 (Φ) の部分は同じになり、次のように除去できる。
(Eq.55)
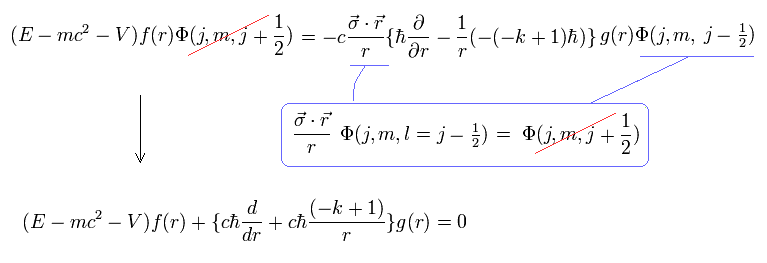
Eq.43 の存在は、ディラックのスピノルに たった1つしか角運動量 (l) がないと、Φ を取り除けないことを意味している。
同様に、Eq.49 は次のように表せる。
(Eq.56)
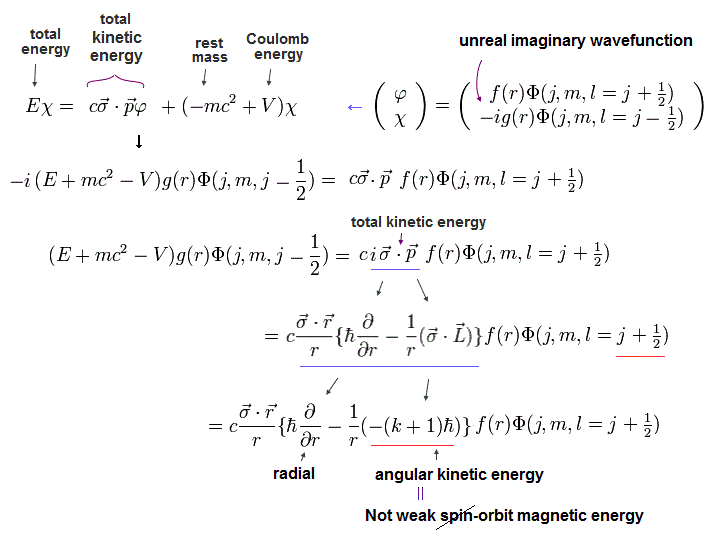
ここで Eq.52 を用いた。
Eq.46 を用いると、 Φ を次のように除去できる。
(Eq.57)
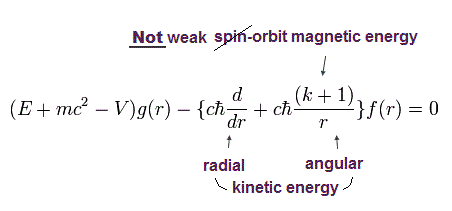
動径方向の波動関数 f(r) と g(r) を次のように置き換える。
(Eq.58)
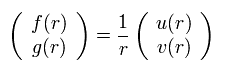
Eq.58 を Eq.55 に代入して、次を得る。
(Eq.59)
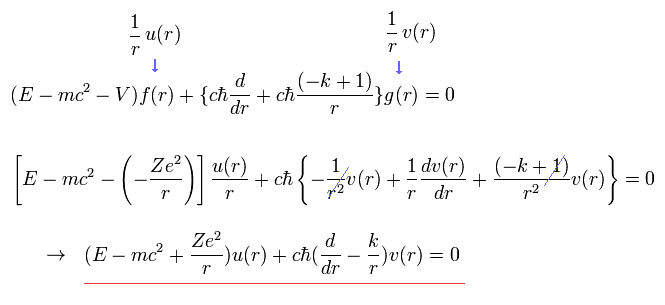
Eq.16 のクーロンポテンシャル V をここで用いている。
同じように、Eq.58 を Eq.57 に代入して、次を得る。
(Eq.60)
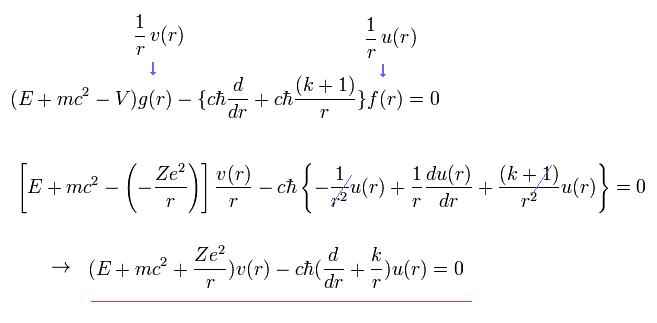
u(r) と v(r) を 次のように展開する。
(Eq.61)
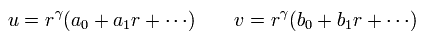
Eq.61 を Eq.59 と Eq.60 に代入して、 γ-1 乗の項を見ると、
(Eq.62)
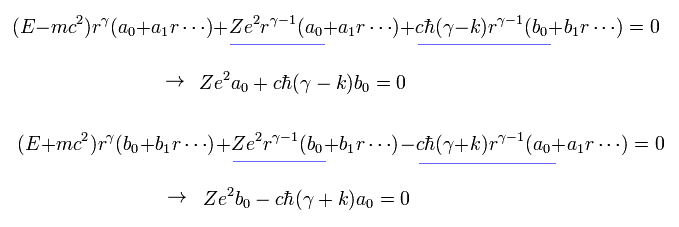
Eq.62 で a0= b0 = 0 の解を避けるには、次の関係式を満足する必要がある。
(Eq.63)
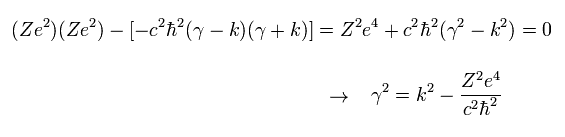
原点での発散を避けるには ( Eq.61 を参照のこと )、γ はプラスになる必要がある。
(Eq.64)
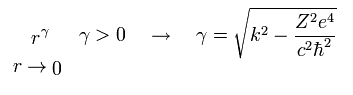
r → ∞ で収束するには、u(r) と v(r) が次を満たす。
(Eq.65)
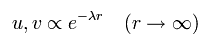
r → ∞ で、 Eq.59 と Eq.60 は、
(Eq.66)
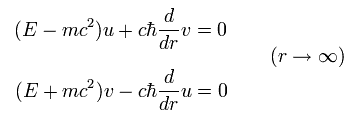
Eq.65 を Eq.66 に代入すると、次を得る。
(Eq.67)
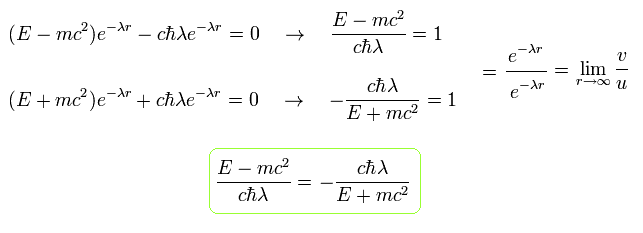
Eq.67 より、 λ (= プラス ) は、
(Eq.68)
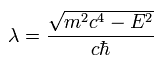
Eq.61 と Eq.65 を考慮すると、 u(r) と v(r) を次のように表せる。
(Eq.69)
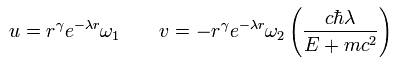
お気づきかもしれないが、Eq.69 の置き換えは シュレデインガーの水素のときに非常に似ている。
つまり、ディラックの水素原子においても、動径の波動関数は 非現実的に ゼロから無限大の範囲になる。
4πε ( Eq.16 参照 ) を Eq.64 の γ に付加すると、微細構造定数 (= α ) を用いて表せる。
(Eq.70)
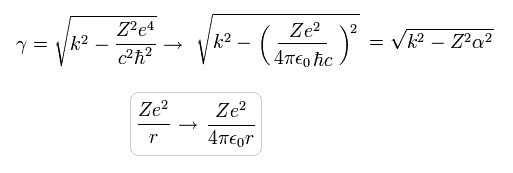
ここで α は、
(Eq.71)
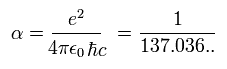
Eq.69 を Eq.59 に代入して、次の関係式を得る ( Eq.68 と Eq.67 の緑の部分を用いて )。
(Eq.72)
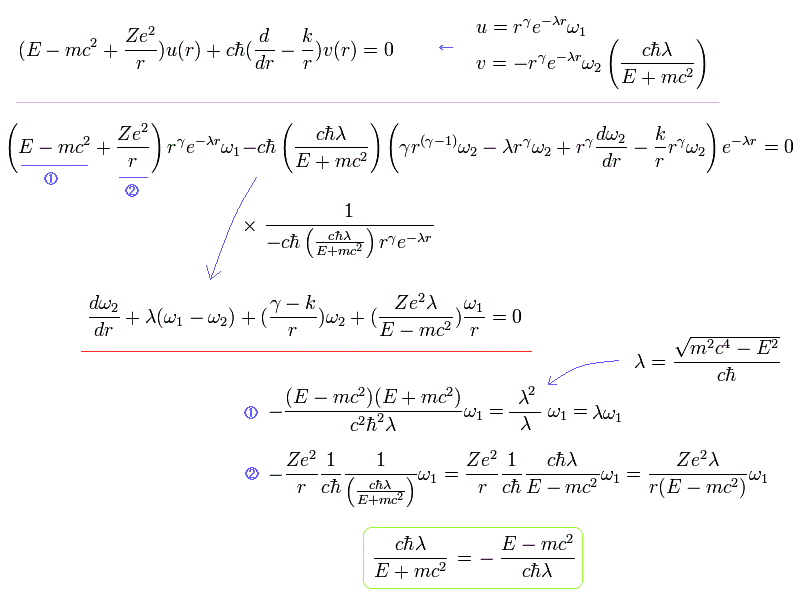
Eq.69 を Eq.60 に代入して、次を得る。
(Eq.73)
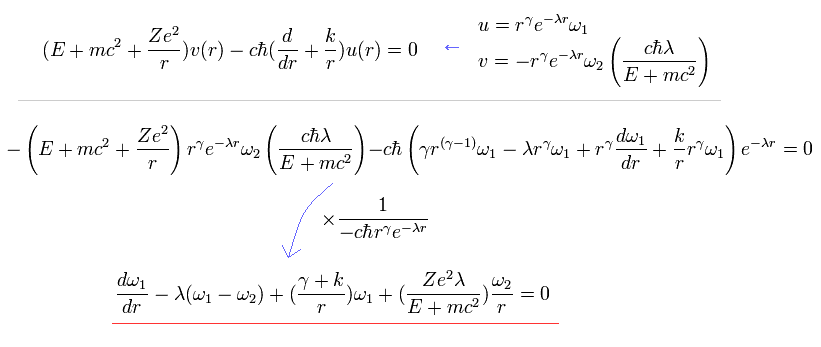
ここで 次を定義する ( Eq.64 と Eq.68 を用いて )。
(Eq.74)
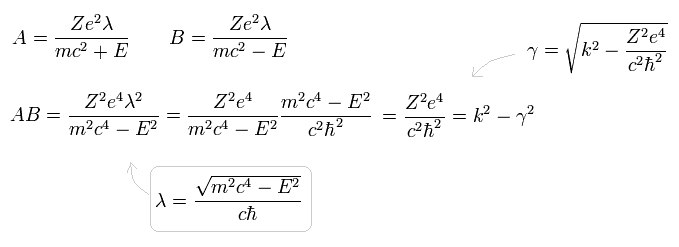
r を x に 次のように置き換える。
(Eq.75)
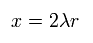
Eq.74 と Eq.75 を用いると、 Eq.73 は、
(Eq.76)
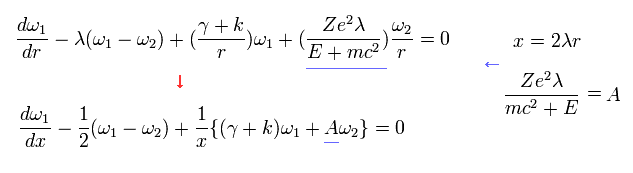
また Eq.72 は、
(Eq.77)
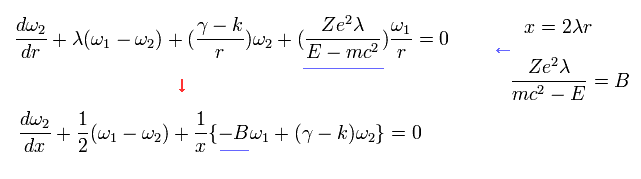
ここで ω1 と ω2 を 次のように展開する。
(Eq.78)
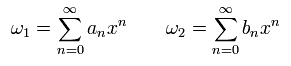
Eq.78 を Eq.76 に代入すると、 x の n - 1 乗 ( = xn-1 ) の項の係数は、
(Eq.79)
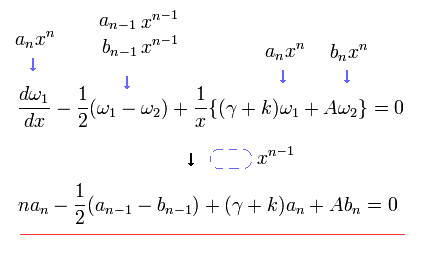
同様に、Eq.78 を Eq.77 に代入すると、 xn-1 の係数は、
(Eq.80)
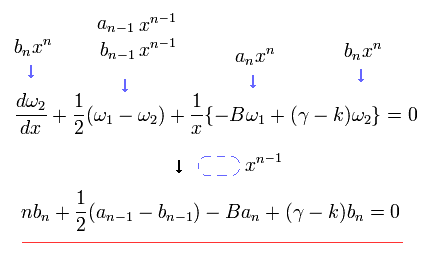
Eq.79 と Eq.80 を足すと、次を得る。
(Eq.81)
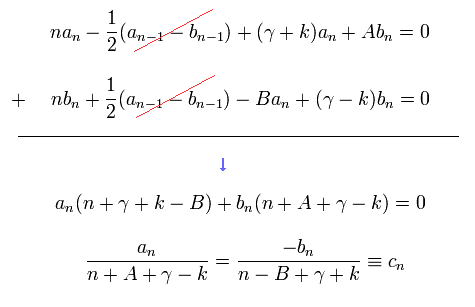
Eq.81 の cn と cn-1 を Eq.79 の a と b に代入して、 Eq.74 を用いると、次の関係式を得る。
(Eq.82)
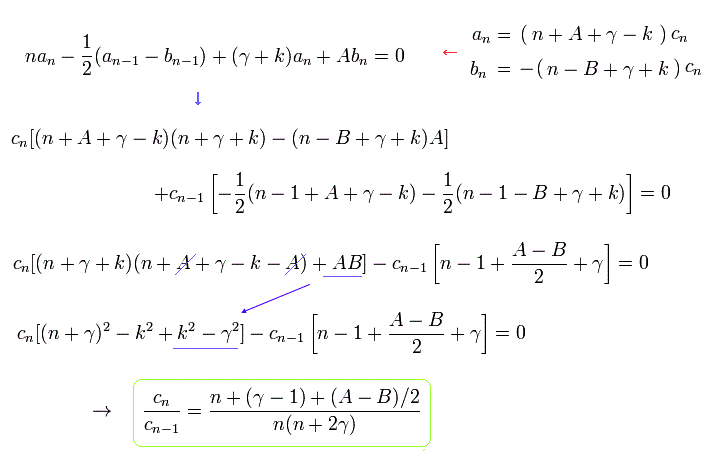
次の置き換えを用いると、
(Eq.83)
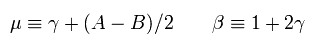
Eq.82 は、
(Eq.84)
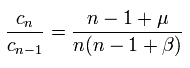
Eq.84 の関係式から、 関数 F(x) を次のように定義できる。
(Eq.85)
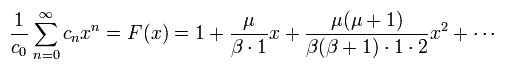
Eq.81 を用いると、 ω1 と ω2 (= Eq.78) は 共通の cn を用いて表すことができる。
(Eq.86)
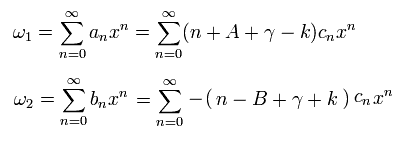
Eq.86 は もし cn の次数を決定すると、上下部のスピノルが cn と同じ次数になることを意味している。
cn の次数は 水素原子のエネルギー準位 (= 動径部分 ) に関係している。これは後で説明する。
( この方法は シュレディンガーの水素原子に似ている。)
結果的に 非実在の 1p1/2 と 1s1/2 は 同じエネルギー準位で、かつ異なった角運動量をもっていることになる。
つまり ディラックの水素原子は 1p1/2、2d3/2 などの 多くの間違った状態を避けられないのである。
F(x) が 無限級数のとき、 F(x) は r → ∞ のとき、指数関数的に発散する。
(Eq.87)
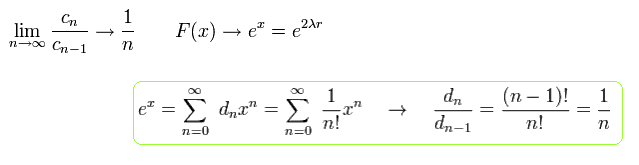
F(x) を 有限の級数にするには、 Eq.84 の μ は 次を満たす必要がある。
(Eq.88)
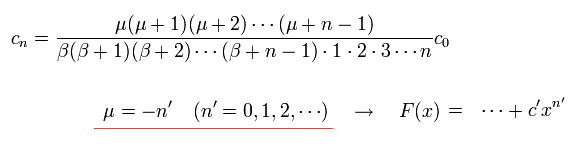
ここで F(x) は x に関して n' 次 になる。
Eq.83 より、
(Eq.89)
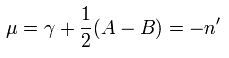
Eq.68 と Eq.74 を Eq.89 に代入して、
(Eq.90)
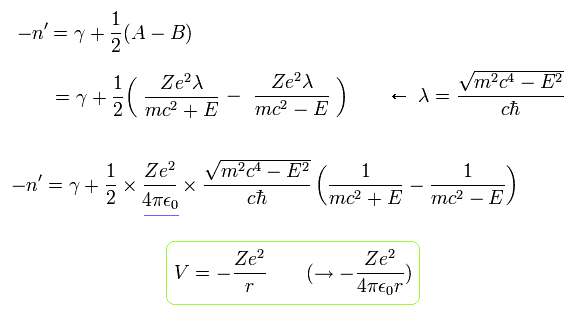
ここで 4πε を戻した。
Eq.71 の微細構造定数 α を用いると、 Eq.90 は、
(Eq.91)
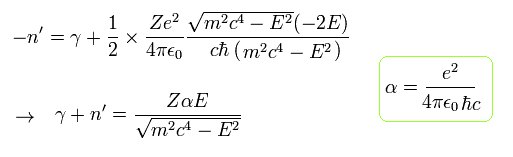
ここで 新たな整数値 n を定義する。
(Eq.92)
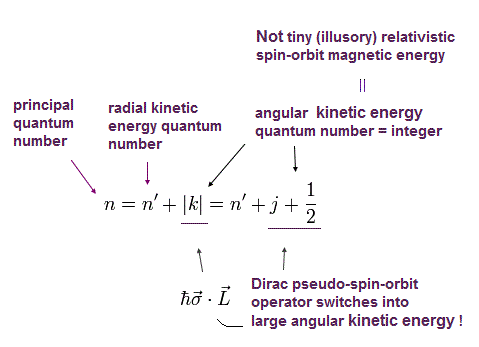
Eq.91 のエネルギー E は ( Eq.70 と |k| = j + 1/2 を用いて )、
(Eq.93)
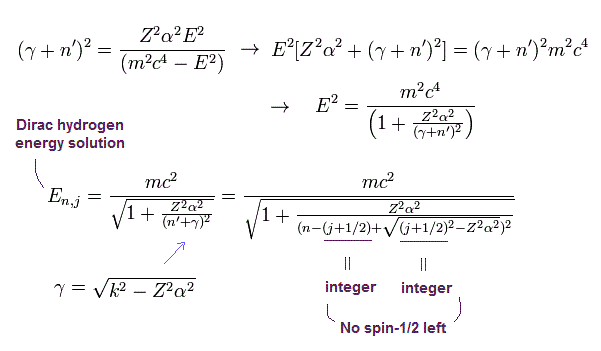
n は主量子数である。
このページに見られるように、 Eq.93 のエネルギー準位は Eq.94 のボーア・ゾンマーフェルト模型のものと 完全に一致している。
(Eq.94)

これはつまり、それらのエネルギー準位は 次のように 互いにちょうど等しい。
2p1/2 (n=2, j=1/2) -------- 楕円。 (nr=1, nφ=1)
2p3/2 (n=2, j=3/2) -------- 円形。 (nr=0, nφ=2)
どうして このような 偶然の一致 が起きてしまったのだろうか?
このセクションでは、水素原子の基底状態の波動関数を計算する。
ご存じのとおり、基底状態は 1S1/2 しかなく、この角運動量はゼロである。
しかし ディラックの水素原子は 下部のスピノルに 非実在の 1P1/2 の状態を含まなければならない。
この事実が ディラックの水素原子が間違いであることを示している。
(Fig.18) 水素原子の基底状態?
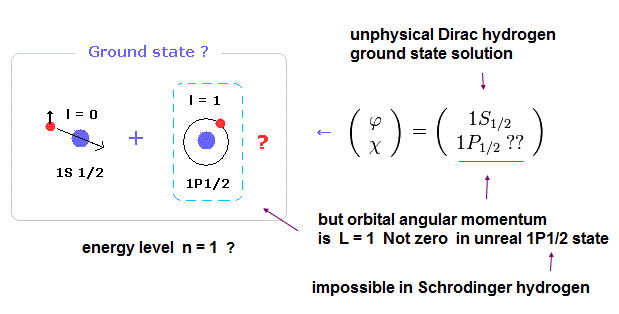
ここで Eq.35 もしくは Eq.36 の固有関数に戻る、1S1/2 (= 基底状態 )について考える。
1S1/2 の状態は 全角運動量 j = 1/2 で、軌道角運動量が l = 0 である。
Eq.35 と Eq.36 によれば、別の奇妙な状態である 1P1/2 も入れなければならないのである ( Eq.95 参照のこと )。
もちろん この 1P1/2 の状態は 量子力学の水素原子には存在しないものである。
なぜなら 1P1/2 は 主量子数 n = 1 で 軌道角運動量が l = 1 だからである。
( ボーア模型では、l=0 の代わりにこの状態が存在する。)
(Eq.95)

この奇妙な状態は ディラック方程式の 4成分のスピノルによって生じる。
ディラック方程式は 相対論的効果を表すのに成功し、かつ エネルギー E と 運動量 p に関して1次の式である。
しかしその代わりに、ディラック方程式は 4 × 4 行列と 4成分のスピノルを使用しなければならない。
もし 4成分のうち 2成分のみしか存在しないと ( Eq.35 や Eq.36 の φ もしくは χ がゼロ )、質量項と運動エネルギー項などを結合することができない。
すると ディラック方程式は壊れてしまう。
また すでに述べたように、ディラックのハミルトニアンと 角運動量演算子 (L) は 交換しないので、L を1つに決められない。
結果的に 1P1/2 の間違った状態が 1S1/2 のエネルギー解を得るのに 必須なのである。
( l = j ± 1/2。下の l が 1S1/2、 上の l が 1P1/2. )
次に 実際に 1S1/2 の固有関数 ( Z = 1、水素 ) を解いてみることにする。
Eq.92 によれば、主量子数 n が 1 ( j = 1/2 )、n' はゼロ になる。
(Eq.96)
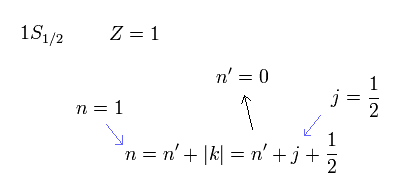
Eq.70 と Eq.93 から、全エネルギー E と γ は、
(Eq.97)
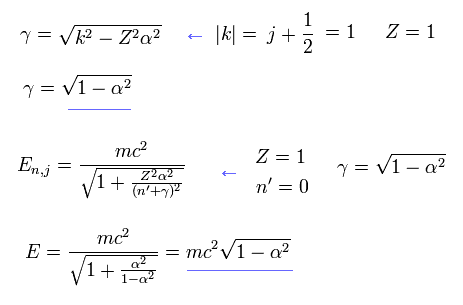
ここで |k| = j + 1/2 = 1.
Eq.97 を Eq.68 に代入して、
(Eq.98)
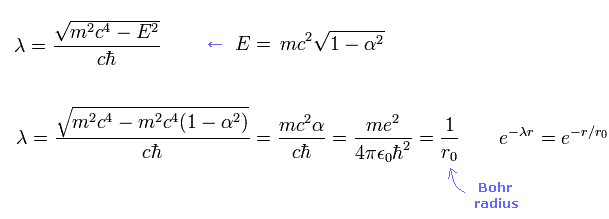
ここで r0 は ボーア半径である。
Eq.98 は ディラックの水素原子の 1S の指数関数部分は シュレディンガーの水素の R10 に等しくなることを意味している。
Eq.97 と Eq.98 を Eq.74 に代入すると、 A は、
(Eq.99)
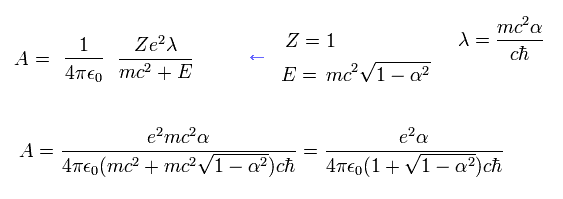
ここで 4πε を戻した。
Eq.86、 Eq.97、 Eq.99 より、 a0 は、
(Eq.100)
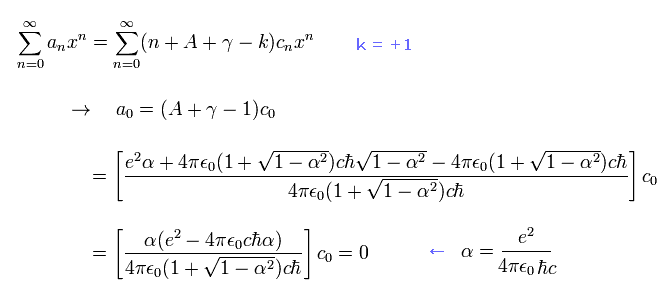
Eq.71 の微細構造定数 α を Eq.100 の最後の行で使用した。
Eq.100 は、 Eq.95 のケース (= 上部が 1P1/2 ) では、ディラックの水素の固有関数がゼロになることを意味している。
(Eq.101)
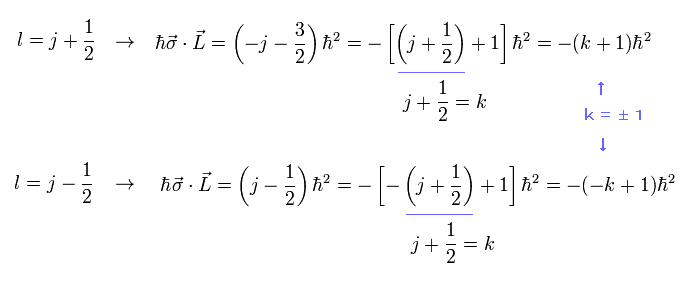
k の符号が逆のとき ( k = 1 → -1 )、軌道角運動量は Eq.101 に示したように 入れ替わる。
そのため k = -1 のとき、 上部が 1S1/2 で、下部が 1P1/2 になる。
この場合では、1S1/2 の固有関数はゼロでなくなる。
(Eq.102)
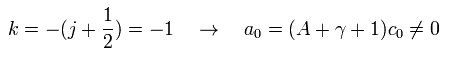
ここで k は マイナスである。
同様に k = -1 のとき、 1P1/2 の下部も ゼロでなくなる。
(Eq.102')
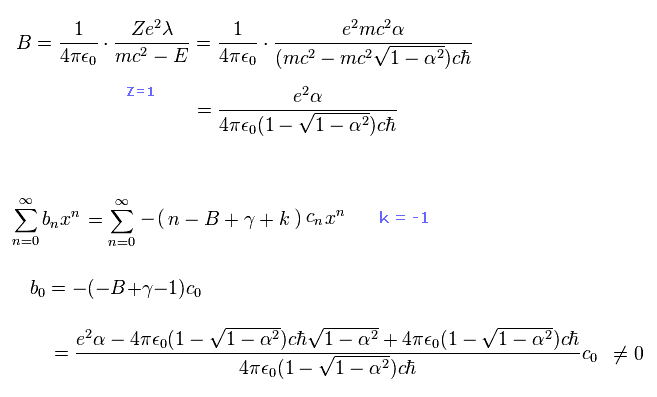
ここで Eq.74、 Eq.81、 Eq.97、 Eq.98 を使用した。
(Eq.103) ディラックの水素原子の基底状態?

上級量子力学 (J.J. サクライ) によると、ディラックの水素の上部スピノルは シュレディンガーの水素原子と関係しているようである。
( しかし、下部スピノルに関する説明を見つけられなかった。)
もちろん、ディラック方程式は これらをミックスするため、非実在の 1P1/2 の状態も必須となる。
結果的に ディラック方程式の水素原子解は 多くの架空の状態 を含んでいることになる。
(1s1/2 と 1p1/2 ??、 2p3/2 と 2d3/2 ??、 3d5/2 と 3f5/2 ?? ... )
これはつまり、ディラックの水素原子は 自己矛盾を含んでおり、ラムシフトの解釈を変える必要があることになる。
ラムシフトは 非常に小さな微細構造よりも さらに小さいものであるため もちろん スペクトル線として じかに確認することはできない。
つまり それが本当に 2S1/2 と 2P1/2 の違いを意味するものかを 知るすべはない。
( このページも参照のこと。 )
それでは 次に n = 2 と j = 1/2 の状態について考えてみる。
幸運なことに、この場合は 2S1/2 ( L= j-1/2 = 0 ) と 2P1/2 ( L = j+1/2 = 1 ) は両方とも存在する。
それでは、これらの状態の 固有関数を得ることができるだろうか?
(Eq.104)
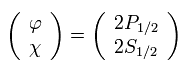
Eq.104 の場合は、2P1/2 の固有関数は
(Eq.105)
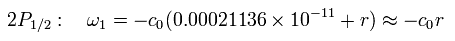
Eq.105 の結果は シュレディンガー方程式の解の 2P1/2 に 似ている。
(また 指数関数の部分も シュレディンガーの n = 2 の解に似ている。)
水素原子の相対論的な効果は とても小さい。
つまり ディラックとシュレディンガー方程式の固有関数が似ていることは 妥当な結果である。
2S1/2 のときはどうであろうか?
2S1/2 の固有関数は
(Eq.106)
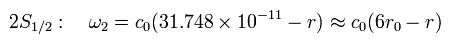
Eq.106 の結果は シュレディンガーの 2S1/2 の解とは 完全に異なっている。
シュレディンガーの 2S1/2 の動径部分は
(Eq.107)
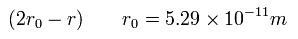
ここで r0 はボーア半径をあらわす。
すでに述べたように 水素原子の相対論的な効果はとても小さい。
そのため、2S1/2 のこの結果は 受け入れることはできない。
(Eq.108)
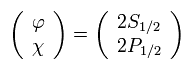
Eq.108 の場合はどうだろうか?
(2S1/2 が スピノルの上部に位置する。もちろん 2S1/2 の角運動量はゼロである。)
Eq.108 の場合は、2S1/2 の固有関数は、
(Eq.109)
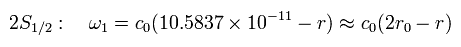
驚くことに、Eq.109 の結果は Eq.107 の シュレデインガーの 2S1/2 の結果と似ている。
しかし、Eq.108 のときの 2P1/2 は
(Eq.110)
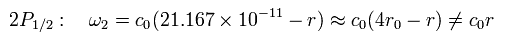
この結果は シュレディンガーの 2P1/2 とは 完全に異なっている。水素の相対論的効果はとても小さいのに関わらずだ。
お気づきのとおり、ディラック方程式では 2P1/2 と 2S1/2 の正確な固有関数を 同時にだすことはできない。
また、これは 2つの誤った状態も含んでいることになる。
不運なことに、ディラック方程式は これらの誤った状態を正しい状態から分離することはできないのである。

2011/4/18 updated This site is link free.