
トップページ (ヘリウムも含む正確な新ボーア模型)
電子スピンは 実在しない。
スピンホール効果は "スピン" を意味しない。
(Fig.1) マグネシウム (= Mg ) の 1、3重項 は "スピン" でなく、クーロン相互作用による。

現在の量子論によれば、アルカリ土類金属の "1重項"、"3重項" は、
スピン・スピン もしくは スピン軌道相互作用によって生じるとしている。
しかし実は、1重項、3重項のエネルギー分裂の間隔は スピン間の磁気エネルギーによる計算値よりも はるかに大きいのである。
( 朝永振一郎の "スピンはめぐる" には それらは 電気的な力 (= クーロン力 ) に起因すると書いてある。 このページ参照のこと。 )
このページでは、実際に スピン・スピン (- 軌道 ) 相互作用の大きさ を計算して、それらと実験値 とを比較して、 このことを確かめることにする。
そして その結果を見れば、1重項、3重項が "スピン" によるという主張自体が 幻想であることが一目瞭然に理解できる。
(Fig.2) Mg では 価電子のうち1つが 3p レベルに 励起される。

このページ や このページでは、スピン軌道相互作用が アルカリ金属の2重項を説明するには弱すぎることを証明した。
もし これらのページを読んでいなければ、最初に読まれるように。
基本的に 1重項、3重項の状態では、マグネシウムの 2つの価電子のうち 1つのみが 3p, 3d, 4s .. などの 上位のエネルギー準位に励起する。 Nist 参照のこと。
( もう1つの価電子は 一番低い 3s 準位に 留まったままである。)
この状態では、これら2つのスピンが 同じ方向を向いたとき、 "3重項" と呼ぶ。
そして 2つのスピンが 互いに反平行のとき、 "1重項" と呼ぶ。
しかし実際は このページで説明していくとおり、"スピン" というのは これらの状態とは
何の関係もないことが分かる。
(Fig.3) 2つのスピンが平行 → S = 1/2 + 1/2 = 1。

各スピンが 1/2 の角運動量を持つ。
そのため 3重項状態では、全スピンは S = 1/2 + 1/2 = 1 になる。なぜなら それらの向きが 互いに平行だからである。
3p 軌道のみが 軌道角運動量 ( L = 1 ) を持つ。
全スピンが 3p の軌道運動 (= L ) に対して 平行か反平行かによって、それは 3つのエネルギー準位に分裂すると 彼らは主張している。
(Fig.4) 3重項状態 ? ← 単なる "数式" で、物理でない。
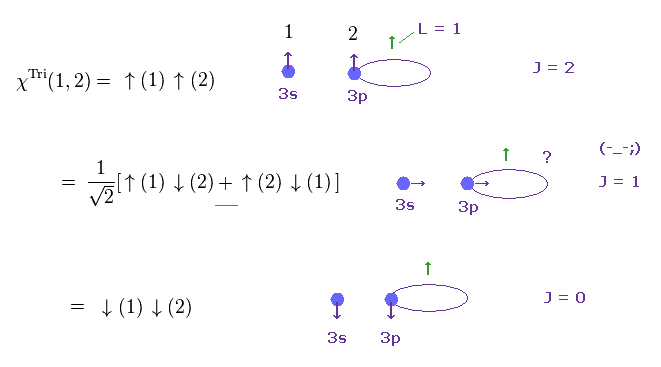
Fig.4 上では、2つのスピン ( S = 1 ) が 軌道角運動量 ( L = 1 ) に対して 平行である。
結果的に 全角運動量は J = S + L = 2 となる。
下の図では、2つのスピンは 軌道運動に 反平行であるため、その 全角運動量は J = L - S = 0 となる。
問題は Fig.4 真ん中の 中間状態である。
もちろん、横方向のスピンまでも認めてしまったら、それはつまり 任意のすべての方向のスピンを認めることを意味し、スペクトラムは 無限の異なる状態に分裂できてしまう。
この中間状態では、1つのスピンは "上方向"、もう1つのスピンは "下方向" を向いてることになっている。
また このサイト (p.10-p.13) にあるように、 Fig.4 の スピンの波動関数 (= χ ) は 変数の交換に対して 対称的な形をしている。
( つまり Fig.4 の "1" と "2" の数を交換しても 全体の符号は 変わらない。 )
しかし これは単なる "数学上" の理由に過ぎず、はっきり言って 物理的な実態は 何も伴っていない。
(Fig.5) 1重項状態 ? ← ± 記号の物理的意味は何なのか?

Fig.4 で述べたように、 3重項の中間状態では、1つの電子は "上方向"、もう1つの電子は "下方向" を向いている。
驚くことに、1重項においても、1つの電子は "上方向"、もう1つの電子は "下方向" を向いているのである。
それなら 3重項と1重項の違いというのは 一体全体 何なのだろうか?
1重項状態では、スピンの波動関数 (= χ ) は 反対称の形をしている。
つまり 1重項の χ で "1" と "2" の数を交換すると 全符号は 逆になる。
(Fig.6) 1つのスピンが "up"、もう1つのスピンが "down" 方向 ← 違いってあるの?

しかし あなたがたも思われたかもしれないが、これら 対称的かそうでないか という理由は はっきり言って 単なる数学上の理由にすぎず、具体的な物理的イメージを 何も伴っていない。
1重項と3重項 (= 中間状態 ) の両方で 1つのスピンが "up"、もう1つのスピンが "down" 方向を向いているということは、現実的な視点からして それらに 何の違いもないことになる。
これらの概念は 例えば 分裂線の数のみの実験事実に合わせるために導入されたと言っていい。
一番肝心な 3重項、1重項のエネルギー分裂幅の事実に関しては まったく考慮されていないのである。
このページで述べていくが、エネルギー分裂幅の実験値は スピン・スピン双極子相互作用よりも
はるかに大きいのである。
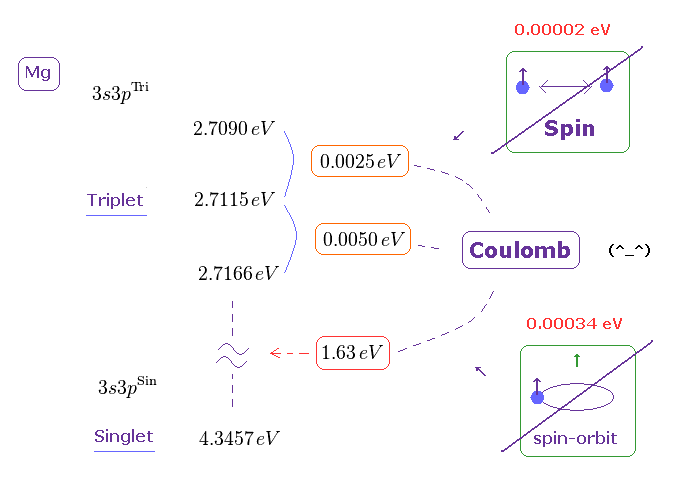
(Fig.7) マグネシウムにおける 3重項、1重項のエネルギー準位。

マグネシウムにおける 3重項、1重項のエネルギー準位は Nist に載っている。
"cm-1" から "eV" のエネルギーの単位変換は Eq.1 のようになる ( このサイト参照のこと。 )
(Eq.1) エネルギー単位の変換。
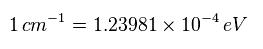
Fig.7 にあるように、3重項と1重項のエネルギーの差は 1.63 eV にもなっている。
この値は スピン相互作用エネルギーの大きさ ( 1.63 eV > 水素の 0.000045 eV。 このサイト参照のこと。 ) よりも はるかに 巨大な値である。
また マグネシウムの n = 3 軌道では、この スピンエネルギーの計算値は 0.00002 eV ぐらいにしかならない。
つまり このエネルギー間隔は 明らかに 強力な クーロン相互作用によるもので、 スピン磁気モーメントとは 何の関係もないのである。
(Fig.8) スピン・スピン磁気エネルギーは 3重項を説明するには 弱すぎる。
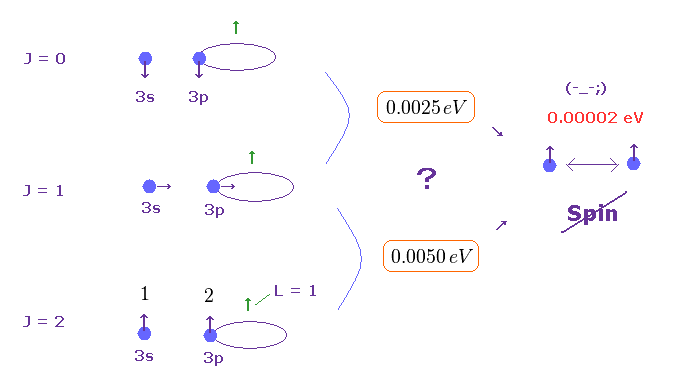
マグネシウムの 3重項の分裂においても、実際のエネルギー分裂幅は スピン・スピン磁気相互作用を想定したものよりも はるかに大きい。
例えば、2つの電子のスピンが 互いに 1.0 × 10-10 メートル (= 約 2 × ボーア半径 ) 離れているとすると、このスピン・スピン 磁気エネルギーは 1.7 × 10-23 J (= 0.00010 eV ) ほどになる。 このサイト (33.10) 参照のこと。
(Fig.9) スピン・スピン磁気相互作用は 非常に小さい。
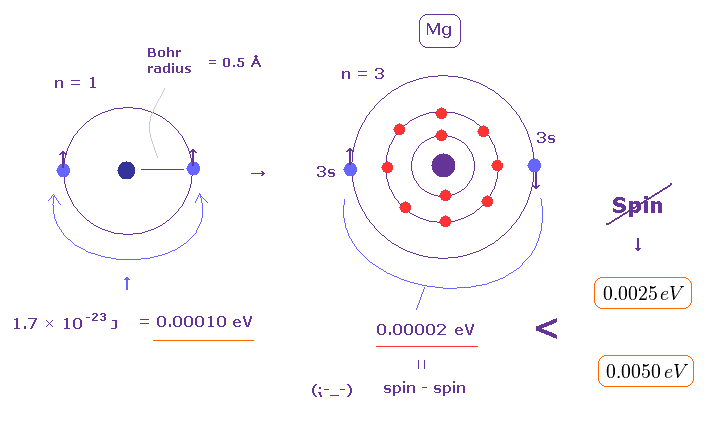
ボーア半径は 水素の基底状態 ( n = 1 ) の平均の半径である。
マグネシウムの価電子は n = 3 の 軌道にある。
つまり Mg の外殻軌道 における 2つのスピン間の距離は ボーア半径よりも はるかに長い。
Fig.9 にあるように、スピン・スピン磁気エネルギー (= 0.00002 eV ) が 実験値の3重項分裂幅 (= 0.0050 eV ) に達することは 不可能である。
(Fig.10) スピン軌道相互作用も 3重項分裂を説明するには 弱すぎる。
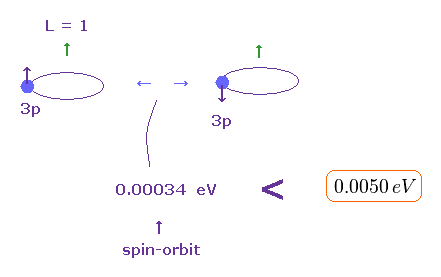
Fig.4 にあるように、3p 軌道の 電子スピンは 軌道角運動量に対して 平行 もしくは 反平行になる。
つまり スピン軌道相互作用エネルギーが この3重項分裂に 関与している可能性もあるわけである。
しかし 実際に このスピン軌道相互作用エネルギーを計算してもらうと分かるが、この効果も
弱すぎて とてもじゃないが 3重項の分裂幅に到達することはできない。
0.00034 eV (= スピン軌道 ) vs. 0.00500 eV (= 実験値 )。
(Fig.11) スピン軌道相互作用は 小さすぎて 3重項、1重項を説明できない。
結果的に これら 3重項、1重項のエネルギー分裂は 非常に弱いスピン・スピン (- 軌道 ) 相互作用ではなく、クーロン力 によるものであることが分かる。
これらの明白な事実にも関わらず、通常の教科書や教育現場では この事実を 一般人や 学生達から
隠し続けているのである。
これは非常に危険であり、一種の詐欺行為と言われても仕方がない。
( "詐欺"は 立派な犯罪の1つなのでご注意を。)
(Fig.12) スピン・スピン磁気双極子エネルギー。
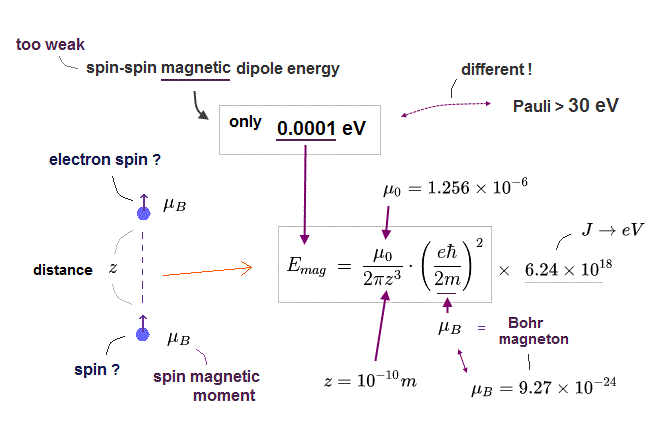
2つのスピン間の距離が "z" のとき、その磁気エネルギー (= Emg ) は Fig.12 のようになる。 このサイト (33.8) も参照のこと。各スピン磁気モーメントは ボーア磁子 (= μB ) である。
ボーア磁子は このサイトにあるように もともと 軌道運動に由来した概念である。
しかし偶然にも スピン磁気モーメントは g因子 = 2 のために ボーア磁子と等しくなる。
このサイト参照のこと。
(Fig.13) スピン・スピン磁気双極子エネルギーの形。 パート II。
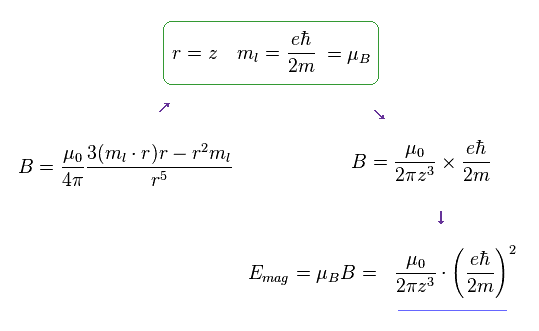
"z" の方向が スピンと異なると、スピンによって生じる磁場 (= B ) の方向は Fig.13 のようになる ( このサイト p.8 や このサイト p.7 も参照のこと )。
"r" が ml (= 磁気モーメント ) に対して (反)平行のとき、この形は Fig.12 にちょうど等しくなる。
そのため 単純な Fig.12 を スピン・スピン磁気エネルギーとして用いる。
(Fig.14)
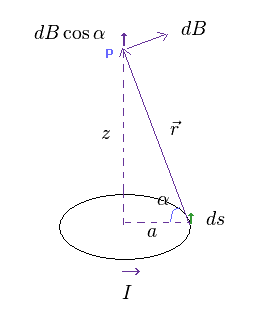
Fig.14 では、円形電流 I は "p" の地点に 磁場 (= B ) を生じる。
この円形の電子軌道によって、z 方向以外の磁場は 打ち消される。
そのため z成分の磁場 (= dB cos α ) のみ残る。
(Eq.2)
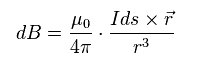
ビオ・サバールの法則 ( このサイト参照のこと ) によれば、磁場 (= B ) は Eq.2 のようになる。
"I" は電流で、 "ds" は 電流切片、 "r" は この切片と "p" 地点間の距離である。
(Eq.3)
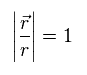
Eq.2 では、"r" 方向の 単位ベクトルは Eq.3 である。
Eq.3 を Eq.2 に用いると、 全磁場の z 成分は 次のようになる。
(Eq.4)
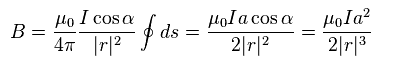
ここでは
(Eq.5)
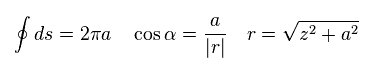
Eq.4 の結果は このサイトと同じである。
Eq.5 と Iπa2 = 磁気モーメント (= ボーア磁子 ) の定義を用いると、 Eq.4 は Eq.6 のようになる。
( 楕円軌道に関しては、 このセクションを参照のこと。 )
(Eq.6)
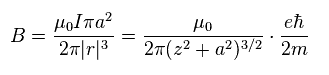
磁気エネルギー (= Emg ) は 磁気モーメント (= μB ) × B で与えられる。
(Eq.7) スピン・スピン磁気エネルギー。
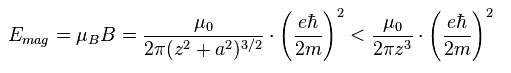
円形電流がスピンだとすると、軌道半径 "a" は Eq.7 右で ほぼゼロになる ( a → 0 )。
( もちろん、実際には この "a" は ゼロでないため、磁気エネルギーは Eq.7 に示したように もっと 小さくなる。 )
Eq.7 の結果は このサイト (33.9) と 同じである。
マグネシウムの外殻軌道の 2つのスピン間の距離 (= z ) が分かれば、Eq.7 の磁気エネルギーの大きさが決まる。
(Fig.15) Mg における 3s 軌道半径の推定値。
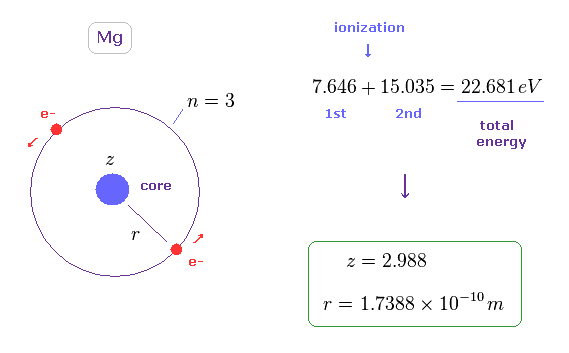
Mg の外殻軌道の 2つのスピン間の平均距離を知るために、Fig.15 の単純なモデルを用いる。
Fig.15 では 2つの価電子が 同じ軌道上 (= 3 ドブロイ波長 ) で、中心電荷 (= 有効電荷 "z" ) の ちょうど反対に位置しながら運動している。
この単純模型は このページ (Table 1) に示したように 実験結果に近い値を与える。
マグネシウムの 1st と 2nd の イオン化エネルギー の和 ( 7.646 + 15.035 = 22.681 eV、 このサイト参照 ) を 全エネルギー ( E = - 22.681 eV ) として用いる。
この全エネルギーを用いると、半径 r = 1.7388 Å と 中心の有効芯電荷 z = 2.988 の値を得る。
この半径は このサイトのものと ほぼ同じである。
詳細な計算方法は このセクション参照のこと。
(Eq.8) 水素様原子の半径。
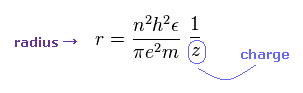
平均の軌道半径は 主量子数の2乗 (= n2 ) に比例し、 中心電荷 (= z ) に反比例する。 このサイト (17.55) 参照のこと。
(Fig.16) Mg の 3s 軌道半径の 粗い推定値 ( z = 3 )。
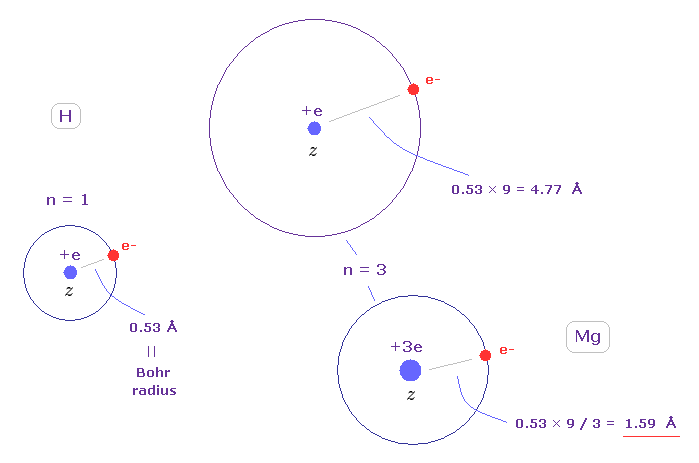
水素の基底状態 ( z = 1, n = 1 ) の平均の半径は ボーア半径 (= 0.53 Å ) である。
つまり n = 3 の準位の軌道半径は 9 × 0.53 = 4.77 Å になる。
Mg2+ の中心の芯電荷を 約 z = 3 とする ( 内殻の軌道間にある隙間のためこの 有効電荷 z は "2" より少し大きくなる )。
この Mg の半径は 0.53 × 9 / 3 = 1.59 Å で、これは Fig.15 の 1.738 Å の結果と似ている。
( もう1つの価電子の影響で、実際の有効電荷は "3" より小さくなる。 )
(Fig.17)
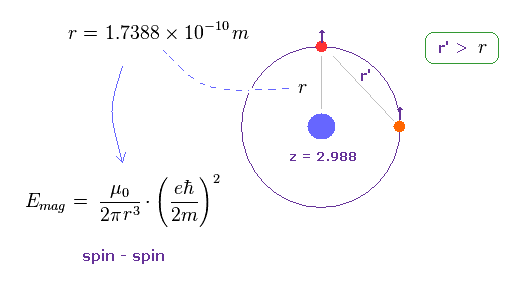
Fig.15 の "r" は Mg の外殻軌道半径である。
Fig.17 に示したように 2つの価電子間の距離 (= r' ) は この半径よりも 長くなる ( r' > r )。
つまり この距離 "r" に基づく スピン・スピン磁気エネルギーが3重項のエネルギー間隔よりも小さければ、すなわち この磁気エネルギーは 実験値に 届かない ということになる。
(Eq.8)
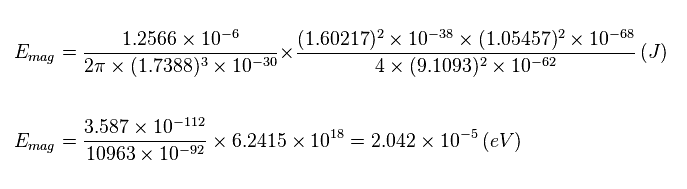
Eq.8 に示したように、スピン・スピン双極子エネルギーは 2.042 × 10-5 eV よりも小さくなる。
この値は非常に小さく、実際の3重項分裂幅 (= 0.0025 もしくは 0.0050 eV、 Fig.7 参照のこと ) の 1/100 倍 ほどしかない。
(Fig.18) スピン・スピン磁気エネルギーは 非常に小さい。
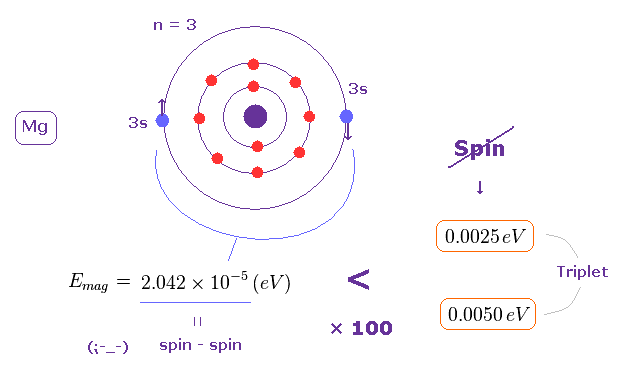
この結果を見れば、スピン・スピン相互作用を用いて 3重項の分裂を説明することが
まったく 不可能であることが 容易に理解できる。
この結果にも関わらず、現在の物理学者達は 決して "スピン" を諦めようとしない。
このことは、 奇妙なスピンとは何かということに関して 彼らが 決して "問う" ことをせず、未知なままに放置している困った事実と 明確にリンクしている。
(Fig.19) スピン軌道相互作用も小さすぎる。
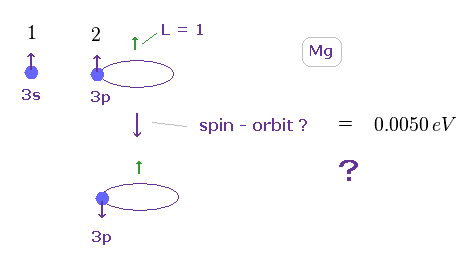
上のセクションでは、スピン・スピン磁気双極子エネルギーは あまりにも小さすぎて、 実際の3重項のエネルギー間隔を 説明できないことを示した。
Mg の 3s3p の電子ペアにおいては 3p 軌道のみ 角運動量 ( L = 1 ) を持つ。
つまり 3p 軌道における 電子スピンの反転が スピン軌道相互作用エネルギーを引き起こす可能性もある。
しかし マグネシウムの 3p 軌道で スピン軌道エネルギーを計算してみると分かるが、この相互作用エネルギーも 小さすぎて 3重項のエネルギー間隔 (= 0.0050 eV、 Fig.7 参照 ) を説明できないことが 容易に分かる。
つまり " 3重項 ( もしくは 1重項 ) = スピン " という図式は 完全に 幻想の産物なのである。
(Fig.20) 水素の (= H ) 2重項 と マグネシウム (= Mg ) の3重項。
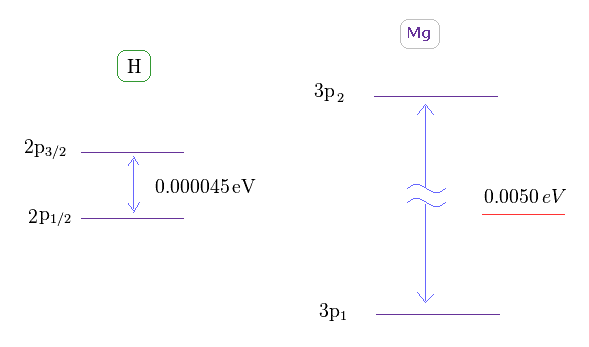
このサイト ( もしくは Nist ) によれば、 水素の微細構造 (= 2p3/2 と 2p1/2 の準位間の 2重項 ) は 約 0.000045 eV である。
一方で、マグネシウムの 3重項は 0.0050 eV ほども大きい。 Nist を参照のこと。
現在の量子力学によれば、3重項の分裂は 3s-3p 軌道における スピンの方向の変化によって
説明されなければならない。
しかし、結局 非常に弱いスピン磁気モーメントでは この大きなエネルギー間隔を まったく再現できないことが分かる。
(Fig.21) マグネシウムの芯電荷は Z = 2 よりも はるかに大きい !?
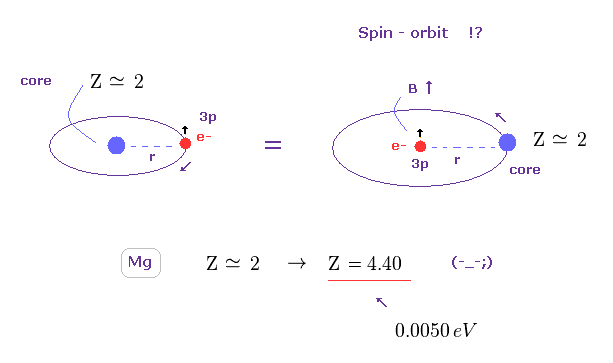
マグネシウムには 2つの価電子がある ( この場合、1つは 3s 軌道、もう1つは 3p 軌道に励起する )。
つまり Ma2+ イオンは 約 Z = +2 の中心の芯電荷を持つことになる。
3p 電子の視点からは、 芯電荷 Z が 3p 電子の周囲を回っており、それが 磁場を生じて、スピン軌道エネルギーの原因になると 現在の理論は主張している。
しかし 実際に スピン軌道相互作用を用いて 3重項の分裂 (= 0.0050 eV ) を再現しようとすると、この芯電荷は Z = 4.40 ほども大きくなってしまう。
この結果は スピン軌道相互作用が Mg の3重項に ( もちろん 1重項にも ) 何の関係もないことを示している。
(Fig.22) スピン軌道相互作用による エネルギー分裂幅 (= ΔE )。
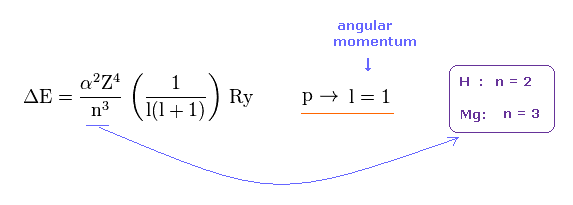
スピン軌道相互作用による エネルギー分裂は Z4 ( Z は 中心電荷 ) に比例し、 n3 ( n は 主量子数 ) に反比例することが知られている。 ここ、 ここ (p.9) 、 ここ など参照のこと。
水素の2重項は n = 2 のエネルギー準位で、この場合の マグネシウムは n = 3 のエネルギー準位である。
両原子において "p" 軌道は 同じ角運動量をもつ ( H と Mg で l = 1 )。
(Fig.23) Mg の中心の芯電荷 Z は どれくらいの大きさか?
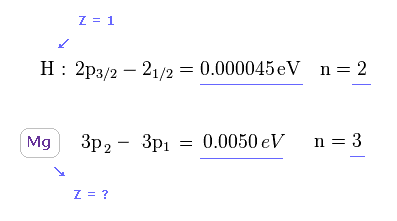
結果的に、Mg と H 間の あまりにも大きなエネルギー差を説明するには Mg の芯電荷は H よりも
はるかに 大きくならなければならない。
( もちろん、 H の 中心電荷は Z = 1 である )。
(Fig.24) Mg の 有効芯電荷が Z = 4.40 ほどに大きくなってしまう !?
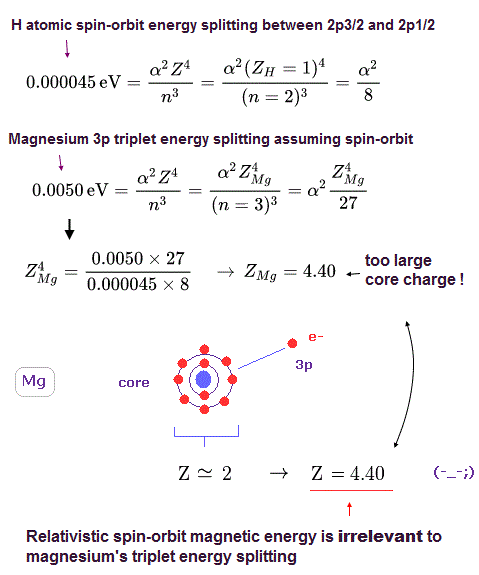
Fig.22 と Fig.23 を用いると ( H と Mg の値を比較して )、Mg の中心芯電荷の大きさを知ることができる。
Fig.24 に示したように Mg のこの電荷は Z = 4.40 ほどに大きくなってしまうことが分かる。
もちろん、この中心の芯電荷量 Z = 4.40 は 現実では あり得ないほど 大きなものである。
この計算結果は スピン軌道相互作用が弱すぎて Mg の3重項の分裂に まったく関与していないことを示している。
(Fig.25) Mg における 有効芯電荷 Z はどれぐらいか?
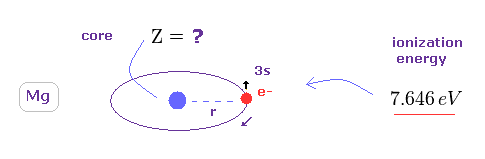
Mg のイオン化エネルギーを基に 本当の有効芯電荷 Z を知ることができる。
Mg の第一イオン化エネルギーは 7.646 eV である。
( この電子は "3s" である。 もちろん "3p" 電子は さらに原子核から離れているため、この Z は もっと小さくなる。 )
(Fig.26)
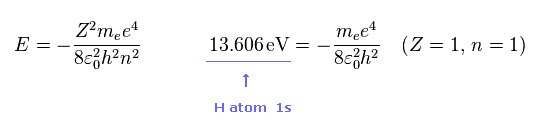
ご存じのとおり、水素の 1s 電子のイオン化エネルギーは 13.606 eV である。
1s の水素では、 Z = 1 と n = 1 である。
(Fig.27) Mg における 有効芯電荷 Z は何か?
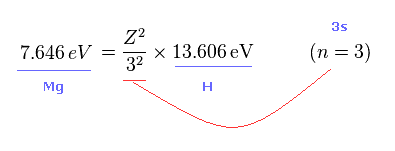
Fig.25 と Fig.26 から Fig.27 の関係式を得る。
Fig.27 の Z は Mg の 3s 電子からの視点の 有効芯電荷である。
( 注意:この Z は Mg の原子核と もう1つの 3s 電子を含む 他のすべての電子の総量を表している。 )
(Fig.28) Mg における 有効芯電荷 Z。
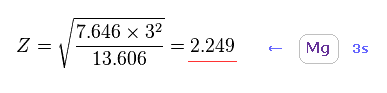
Fig.27 を解くと、本当の有効芯電荷 Z = 2.249 を得る。
この Z は もう1つの 3s 電子の効果も含んでいるため、Fig.15 の値よりも 小さくなる。
(Fig.29) 本当の芯電荷と "偽の" 芯電荷。
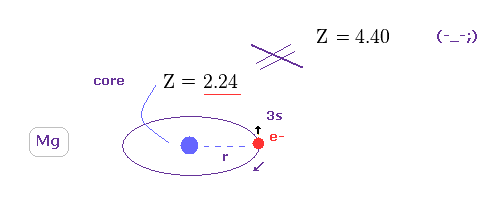
Fig.28 ( 本当の Z = 2.24 ) と Fig.24 ( スピン軌道相互作用を仮定した Z = 4.40 ) を比較すれば、スピン軌道相互作用が 弱すぎて とてもじゃないが Mg の3重項を説明できないことが分かる。
(Fig.30) Mg の 3重項、1重項は "スピン" と何の関係もない。

本当の有効芯電荷を用いると、スピン軌道結合エネルギーは 0.00034 eV ぐらいにしかならないことが分かる。
Fig.30 を見て分かるように、1重項と3重項間のエネルギー差は 非常に大きい (= 1.63 eV )。
つまり この大きなエネルギーギャップを 非常に弱いスピンで説明することは もっと不可能であることが分かる。
現在の理論では、この大きなエネルギーギャップ (= 1.63 eV ) は Fig.31 ( もしくは このサイト参照 ) にあるように、波動関数の 対称性、反対称性の違いによって生じることになっている。
(Fig.31) "対称性" と "反対称性" の波動関数は 大きなエネルギーギャップを起こせるのか?
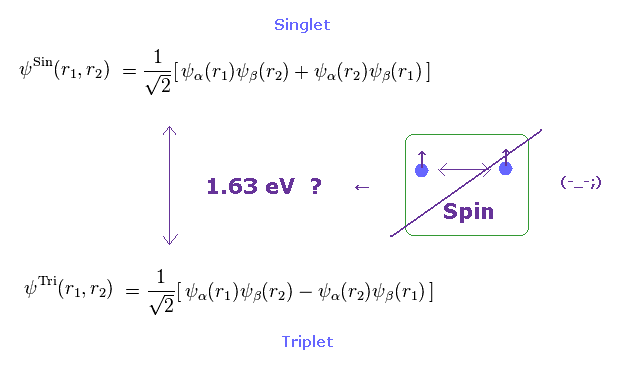
しかしもちろん、上のセクションで示したように、スピン・スピン相互作用 (= 0.00002 eV ) と スピン軌道相互作用 (= 本当の芯電荷 Z を用いた 0.00034 eV ) では 1.63 eV の値には 到底届かない。
この事実にも関わらず、現在の物理学者達は 何としてでも 1重項と3重項を 非現実的な "スピン" に 関連させようとしている。
この "スピン" の語句の誤使用は 明らかに 一般の人達に 誤解を与えている最大の原因になっている。
3重項の中では、それらの波動関数は 共通の形 (= Fig.31 下にあるように 反対称 ) である。
つまり 3重項のエネルギー分裂に この 対称性、反対称性の ロジックは
使用できない。
つまり 3重項は 純粋に スピン・スピン (- 軌道 ) 相互作用で 説明できなければならないのだが、それが 弱すぎるわけである。
結論からして、マグネシウムの3重項と1重項は 強力なクーロン力によって生じ、スピンとは何の関係もないことが 一目瞭然に分かる。
(Fig.32) Ca の 3重項、1重項の大きさは スピン・スピン (- 軌道 ) 相互作用では説明できない。
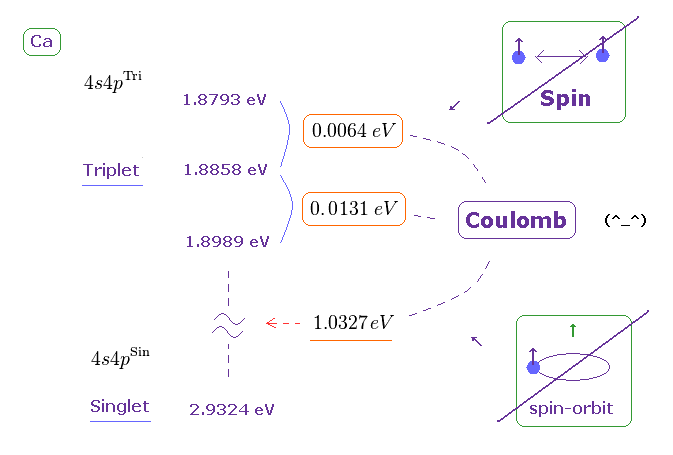
3重項、1重項のエネルギー準位は このサイトに載っている。
エネルギーの単位を変換する ( cm-1 → eV )。
(Eq.9)
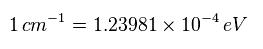
すると Fig.32 の値を得ることができる。
Fig.32 (= Ca ) と Fig.30 (= Mg ) を比較すると、Ca での 3重項でのエネルギー分裂幅は Mg のよりも 大きいことが分かる。
つまり、 ますます スピン・スピン (- 軌道 ) 相互作用で この3重項を説明することが不可能になる。
(Fig.33) Ca における ヘリウム様模型での 軌道半径。
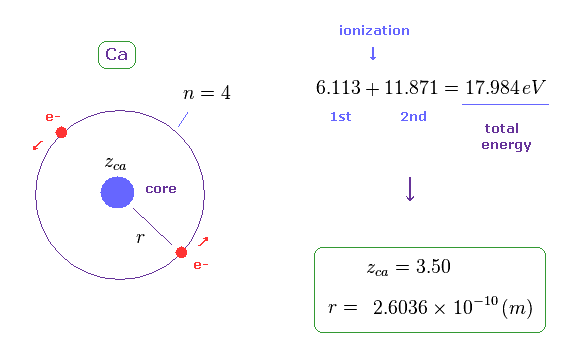
Ca の 1st と 2nd のイオン化エネルギーの合計は このサイトにあるように 17.984 eV である。
Fig.15 のように、Ca においても ヘリウム様モデルを想定し、その全エネルギーを -17.984 eV と仮定する。
このモデルでは、 軌道半径 (= r ) は 2.6036 Å になり、これは Mg よりも 長い。
計算方法は このセクションと同じである。
(Fig.34) Ca では スピン・スピン磁気エネルギーは 3重項の分裂幅の わずが 1/1000 しかならない。
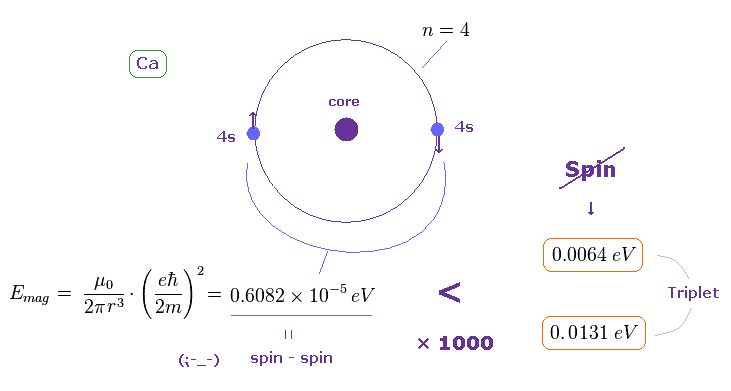
Fig.33 の近似的な半径を用いると、Ca の外殻軌道における スピン・スピン磁気双極子エネルギーは 非常に小さいことが分かる。
(= 0.6082 × 10-5 eV。計算方法は このセクション参照。 )
この結果からは カルシウムにおいても 3重項を スピン・スピン磁気相互作用で説明することが
不可能であることが分かる。
(Fig.35) H の 2p の2重項と Ca の4p の3重項。
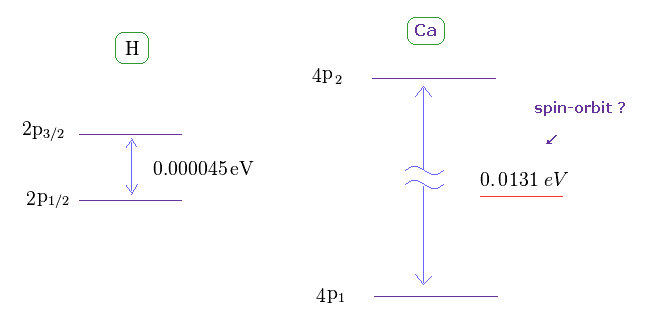
Ca の3重項のエネルギー間隔は 水素の 2p の2重項よりも はるかに
大きい。
上で述べたように、スピン・スピン相互作用は この3重項とは 何の関係もない。
つまり スピンがこの3重項に関与しているとしたら、あとは スピン軌道相互作用しか残っていないことになる。
(Fig.36) 有効芯電荷 Z が 非現実的なくらい 大きくなる ( Z = 2 → 6.946 )。
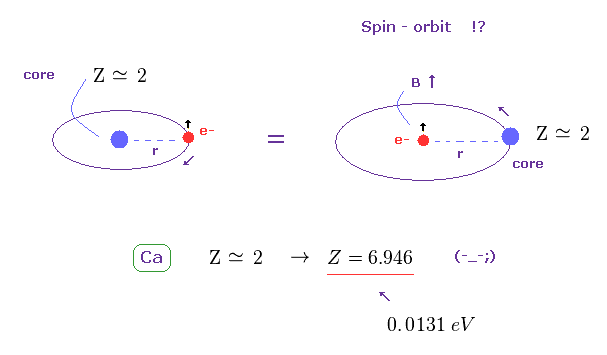
このセクションのように、 Ca の3重項を スピン軌道相互作用によると仮定して、有効芯電荷 Z を計算する。
すると、0.0131 eV もの 大きなエネルギー分裂幅を説明するのに この有効芯電荷 Z の値は 非現実的なくらい 大きくなることがわかる ( Z = 6.946 )。
この結果を見れば、 スピン軌道相互作用も この3重項に 何の関与もしていないことが一目瞭然である。
(Fig.37) 本当の 有効芯電荷 Z = 2.68。
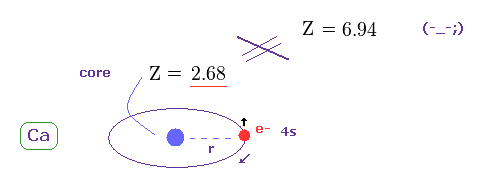
このセクションのように、 第一イオン化エネルギー、 6.113 eV を用いて 本当の有効芯電荷 Z を知ることができる。
イオン化エネルギーに基づく この "真の" 有効芯電荷 (= 2.68 ) は Z = 6.94 よりも はるかに小さい。
またもや、スピン軌道相互作用が 3重項分裂と 何の関係もないことが証明できた。
(Fig.38) Sr の 3重項、1重項の大きさは スピン・スピン (- 軌道 ) 相互作用では説明できない。
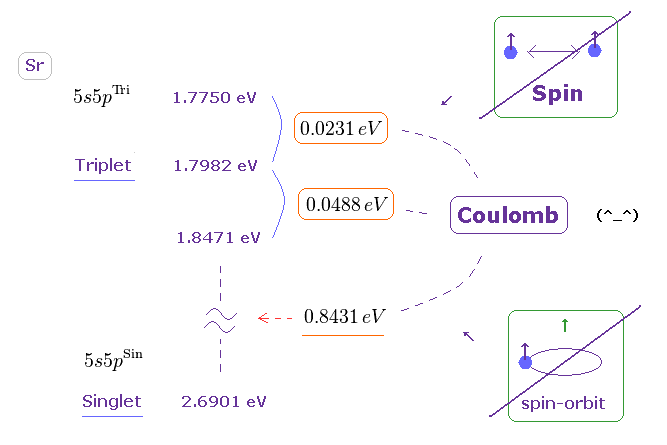
3重項、1重項のエネルギー準位は このサイトに載っている。
エネルギーの単位を変換する ( cm-1 → eV )。
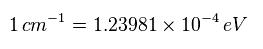
すると Fig.38 の値を得ることができる。
Fig.38 (= Sr ) と Fig.30 (= Mg ) を比較すると、Sr での 3重項でのエネルギー分裂幅は Mg のよりも 大きいことが分かる。
つまり、 ますます スピン・スピン (- 軌道 ) 相互作用で この3重項を説明することが不可能になる。
(Fig.39) Sr における ヘリウム様模型での 軌道半径。
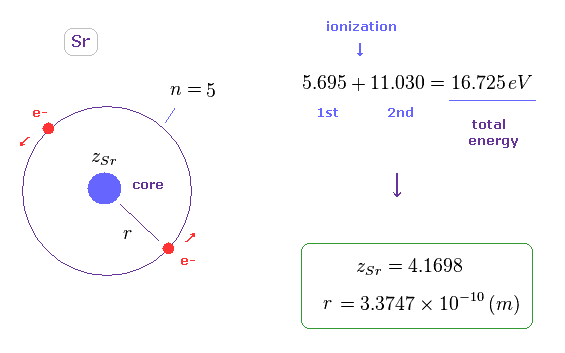
Sr の 1st と 2nd のイオン化エネルギーの合計は このサイトにあるように 16.725 eV である。
Fig.15 のように、Ca においても ヘリウム様モデルを想定し、その全エネルギーを -16.725 eV と仮定する。
このモデルでは、 軌道半径 (= r ) は 3.3747 Å になり、これは Mg よりも 長い。
計算方法は このセクションと同じである。
(Fig.40) Sr では スピン・スピン磁気エネルギーは 3重項の分裂幅の わずが 1/10000 しかならない。
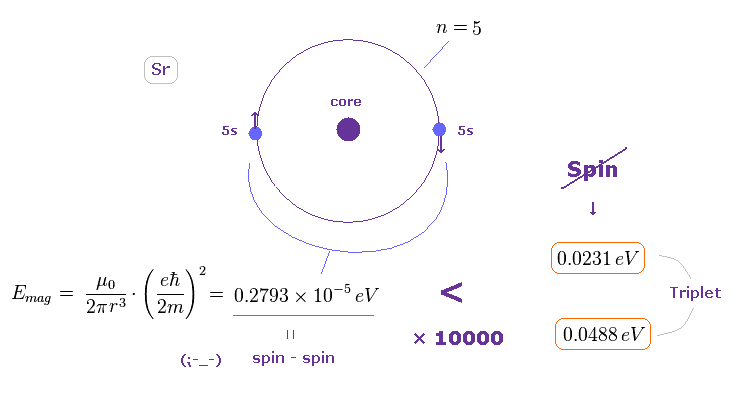
Fig.39 の近似的な半径を用いると、Sr の外殻軌道における スピン・スピン磁気双極子エネルギーは 非常に小さいことが分かる。
(= 0.2793 × 10-5 eV。計算方法は このセクション参照。 )
この結果からは ストロンチウムにおいても 3重項を スピン・スピン磁気相互作用で説明することが
不可能であることが分かる。
(Fig.41) H の 2p の2重項と Sr の5p の3重項。
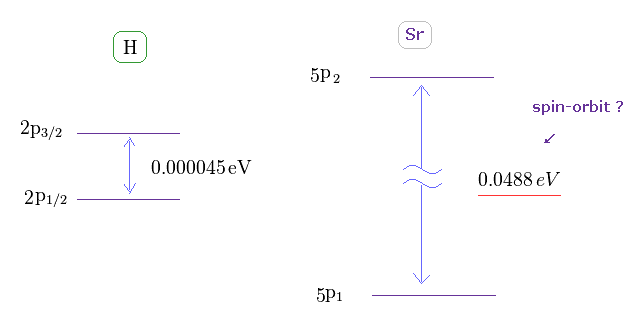
Sr の3重項のエネルギー間隔は 水素の 2p の2重項よりも はるかに
大きい。
上で述べたように、スピン・スピン相互作用は この3重項とは 何の関係もない。
つまり スピンがこの3重項に関与しているとしたら、あとは スピン軌道相互作用しか残っていないことになる。
(Fig.42) 有効芯電荷 Z が 非現実的なくらい 大きくなる ( Z = 2 → 11.409 )。
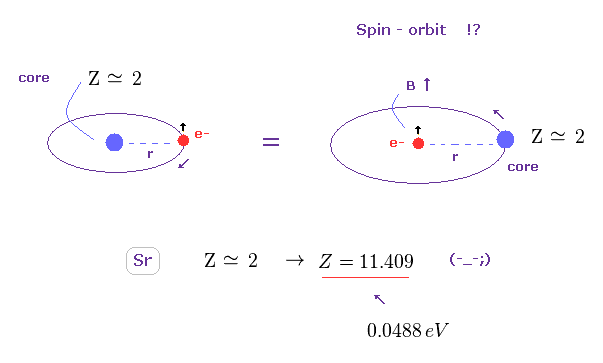
このセクションのように、 Sr の3重項を スピン軌道相互作用によると仮定して、有効芯電荷 Z を計算する。
すると、0.0488 eV もの 大きなエネルギー分裂幅を説明するのに この有効芯電荷 Z の値は 非現実的なくらい 大きくなることがわかる ( Z = 11.409 )。
この結果を見れば、 スピン軌道相互作用も この3重項に 何の関与もしていないことが一目瞭然である。
(Fig.43) 本当の 有効芯電荷 Z = 3.23。
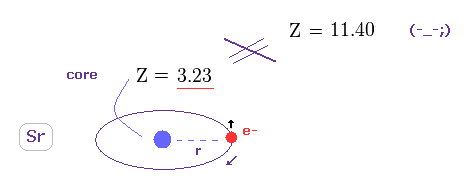
このセクションのように、 第一イオン化エネルギー、 5.695 eV を用いて 本当の有効芯電荷 Z を知ることができる。
イオン化エネルギーに基づく この "真の" 有効芯電荷 (= 3.23 ) は Z = 11.409 よりも はるかに小さい。
またもや、スピン軌道相互作用が 3重項分裂と 何の関係もないことが証明できた。
(Fig.44) Ba の 3重項、1重項の大きさは スピン・スピン (- 軌道 ) 相互作用では説明できない。
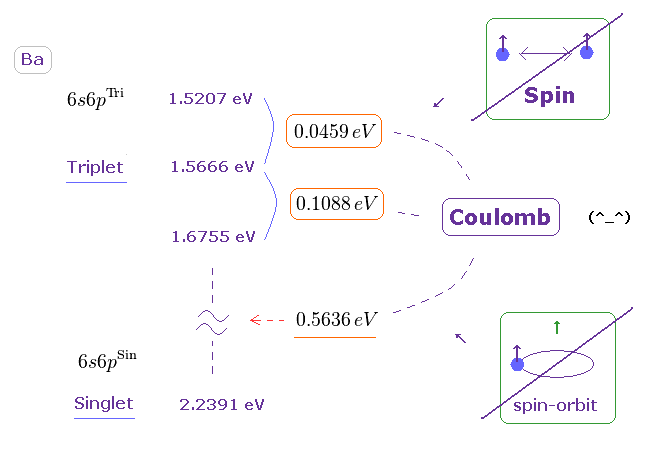
3重項、1重項のエネルギー準位は このサイトに載っている。
エネルギーの単位を変換する ( cm-1 → eV )。
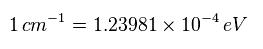
すると Fig.44 の値を得ることができる。
Fig.44 (= Ba ) と Fig.30 (= Mg ) を比較すると、Ba での 3重項でのエネルギー分裂幅は Mg のよりも 大きいことが分かる。
つまり、 ますます スピン・スピン (- 軌道 ) 相互作用で この3重項を説明することが不可能になる。
(Fig.45) Ba における ヘリウム様模型での 軌道半径。
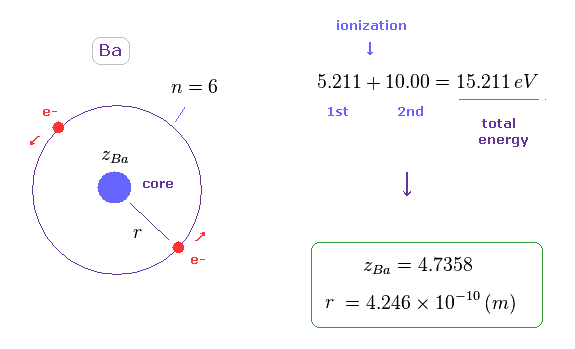
Ba の 1st と 2nd のイオン化エネルギーの合計は このサイトにあるように 15.211 eV である。
Fig.15 のように、Sr においても ヘリウム様モデルを想定し、その全エネルギーを -15.211 eV と仮定する。
このモデルでは、 軌道半径 (= r ) は 4.246 Å になり、これは Mg よりも 長い。
計算方法は このセクションと同じである。
(Fig.46) Ba では スピン・スピン磁気エネルギーは 3重項の分裂幅の わずが 1/10000 しかならない。
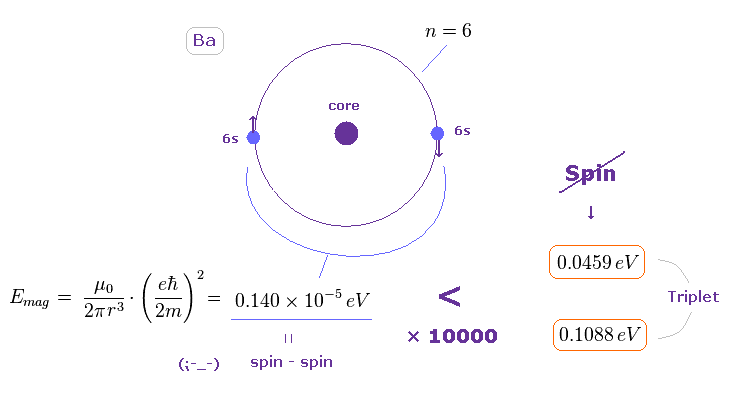
Fig.45 の近似的な半径を用いると、Ba の外殻軌道における スピン・スピン磁気双極子エネルギーは 非常に小さいことが分かる。
(= 0.140 × 10-5 eV。計算方法は このセクション参照。 )
この結果からは バリウムにおいても 3重項を スピン・スピン磁気相互作用で説明することが
不可能であることが分かる。
(Fig.47) H の 2p の2重項と Ba の6p の3重項。
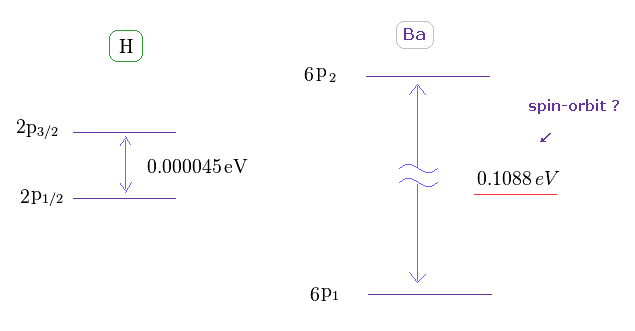
Ba の3重項のエネルギー間隔は 水素の 2p の2重項よりも はるかに
大きい。
上で述べたように、スピン・スピン相互作用は この3重項とは 何の関係もない。
つまり スピンがこの3重項に関与しているとしたら、あとは スピン軌道相互作用しか残っていないことになる。
(Fig.48) 有効芯電荷 Z が 非現実的なくらい 大きくなる ( Z = 2 → 15.984 )。
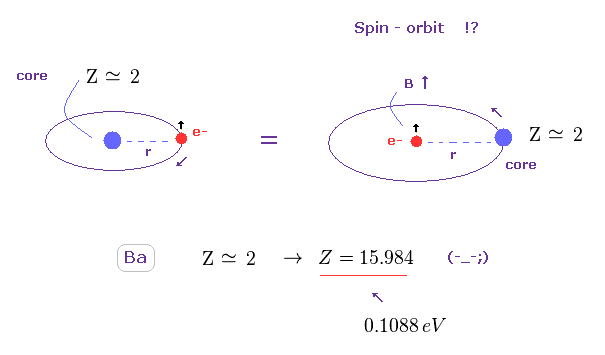
このセクションのように、 Ba の3重項を スピン軌道相互作用によると仮定して、有効芯電荷 Z を計算する。
すると、0.1088 eV もの 大きなエネルギー分裂幅を説明するのに この有効芯電荷 Z の値は 非現実的なくらい 大きくなることがわかる ( Z = 15.984 )。
この結果を見れば、 スピン軌道相互作用も この3重項に 何の関与もしていないことが一目瞭然である。
(Fig.49) 本当の 有効芯電荷 Z = 3.71。
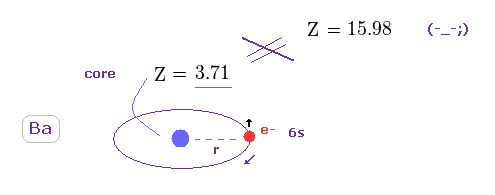
このセクションのように、 第一イオン化エネルギー、 5.211 eV を用いて 本当の有効芯電荷 Z を知ることができる。
イオン化エネルギーに基づく この "真の" 有効芯電荷 (= 3.71 ) は Z = 15.984 よりも はるかに小さい。
またもや、スピン軌道相互作用が 3重項分裂と 何の関係もないことが証明できた。
(Fig.50) カルシウム (= Ca ) のエネルギー準位。
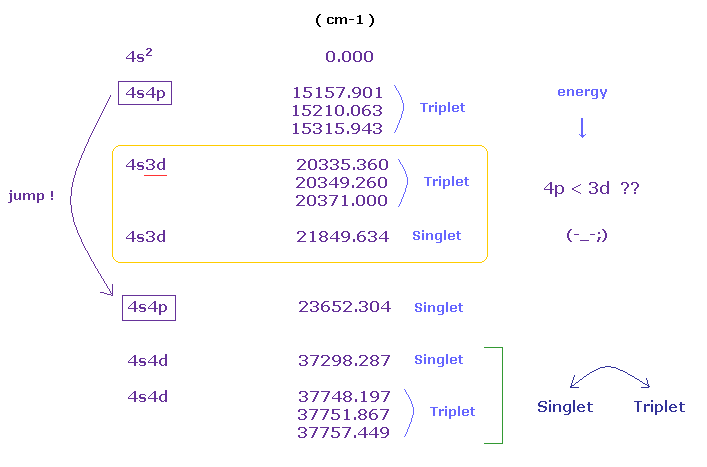
Ca のエネルギー準位 (= Nist ) を注意深く見ると、それらの量子番号や 順番が 非常に不自然であることが分かる。
通常の周期表では、 "3d" 軌道は 4p 軌道よりも エネルギー準位で 低い ことになっている。
しかし Fig.50 を見ると分かるが、 4p 軌道 (= 3重項 ) のほうが 3d 軌道よりも 低くなっている。
( Fig.50 では、 一番トップ (= 4s2 ) が 基底状態であり、下方へ行くほど 高いエネルギー準位であることを示している。 )
また 4s4d の準位では、 3重項、1重項の順番が 逆転している。
( 通常 3重項 → 1重項なのに、 4s4d では、 1重項 → 3重項である。 )
(Fig.51) Mg と Sr のエネルギー準位 "4f" が Mg のみに現れる?
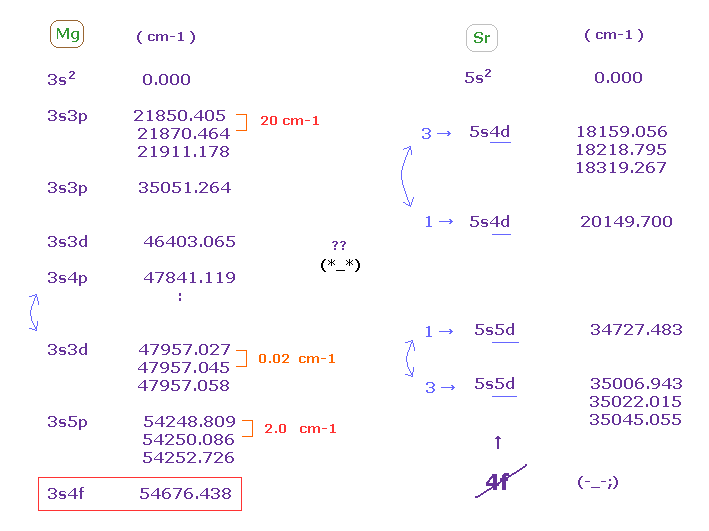
マグネシウムでは、 3重項の エネルギー間隔は バラバラである。
( 3s3p-- 20 cm-1, 3s3d-- 0.02 cm-1, 3s5p-- 2.0 cm-1 ).
また "4f" のエネルギー準位が マグネシウムのみに現れ、 ストロンチウム や バリウムには 現れていない。
これは奇妙である。
"3d" 軌道は エネルギー準位で "4p" よりも低いはずだが、Mg では"3s4p" のほうが 3s3d よりも "低く"なっている。
これもまた奇妙である。
Sr では、5s4d において "3重項" (= 3 ) が 最初に現れるが、 5s5d では "1重項" (= 1 ) が 最初に現れる。
これもまた 人為的な操作の1つである。
つまり これら 3重項、1重項の概念は 非現実的な量子数のみを考慮して 考案されたと言っていい。
彼らは 一番重要な エネルギーの大きさや それらの順番に関しては 完全に無視しているのである。
(Sp.1)
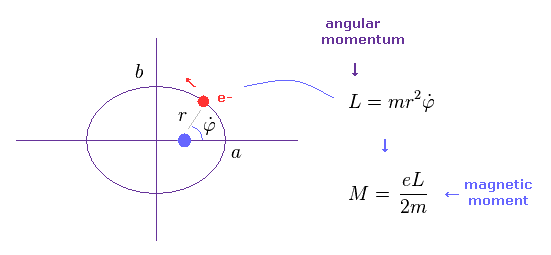
上のセクションでは、単純な円形軌道を扱った。
このセクションでは Sp.1 に示したように 楕円軌道の磁気モーメントが 円形軌道と同じになることを示す。
(Sp.2)
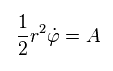
中心力の系では、Sp.2 に示すように 面積速度 (= A ) は 一定である。
(Sp.3)
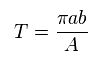
楕円形の全面積は "πab" に等しい。
軌道1周の周期 (= T ) は (= πab ) / A で与えられる。
Sp.2 と Sp.3 を用いると、 電流 I は、
(Sp.4)
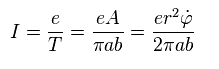
磁気モーメント (= M ) は 電流 I × 面積 で与えられる。
( どんな形でも 微小ループに分割すれば、この法則が適用できることが分かる。 )
結果的に、
(Sp.5)
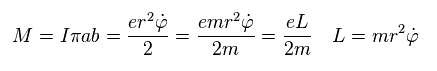
"3p" 軌道は 1 × ħ の角運動量を持つ。
ħ を Sp.5 に代入すると、 3p の軌道磁気モーメントとして "ボーア磁子" を得ることができる。
(Sp.6) 3p = ボーア磁子。
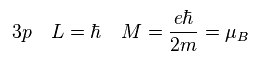
(Sp.7) マグネシウムの 3s の外殻軌道。
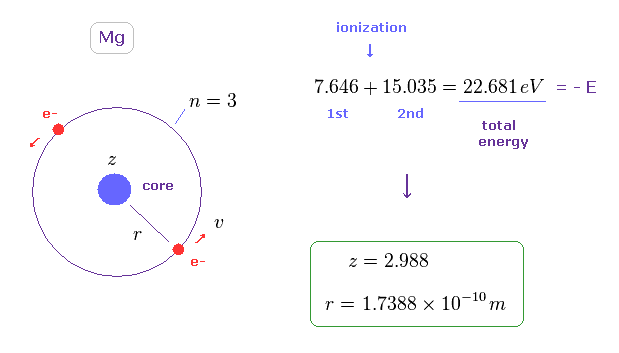
Sp.7 の マグネシウムの模型では、2つの 3s の外殻電子が 共通の軌道上の互いに反対の位置を 速度 "v" で運動している。
芯部分 (= Mg 原子核 + 他のすべての内殻電子 ) の 有効芯電荷を"z" とする。
また 軌道半径を "r" とする。
遠心力とクーロン力が等しいとして
(Sp.8)
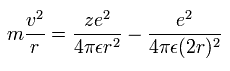
ここでは "m" は 電子の質量である。
左辺は 遠心力で 右辺の最初の項は 芯部分と 各電子間の クーロン力である。
2項目は 2つの電子間の反発力である。
円形軌道の円周を ドブロイ波長 ( λ = h/mv ) の整数倍 (= n ) と仮定する。
(Sp.9)
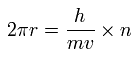
全エネルギー E は 2つの電子の 運動エネルギーと クーロンポテンシャルエネルギーの和であるため、
(Sp.10)
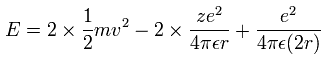
Sp.10 の 全エネルギー E は 1st と 2nd のイオン化エネルギーの和 ( E = -22.681 eV ) に等しいとする。
Sp.8-Sp.10 の連立方程式を解くと、半径 "r" と 有効電荷 "z" を得ることができる。
Sp.9 から、
(Sp.11)
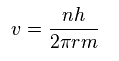
Sp.11 を Sp.8 に代入して、次を得る。
(Sp.12)
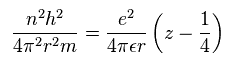
Sp.12 から、
(Sp.13)
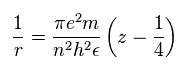
Sp.11 と Sp.13 を Sp.10 に代入して、
(Sp.14)
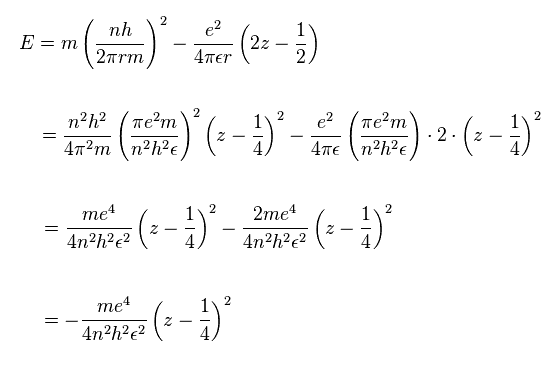
ここで 2つの価電子を持つ Mg を ヘリウム様原子のように考える。
これら2つの外殻電子の全エネルギーを Sp.15 のように 1st と 2nd のイオン化エネルギーの和 ( このサイト参照 ) と考える。
(Sp.15)

Sp.15 ( "eV" → "J" ) と n = 3 を Sp.14 に代入して、
(Sp.16)
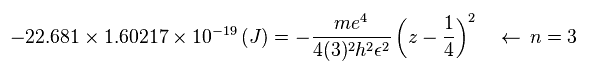
次の値を用いると、
(Sp.17)
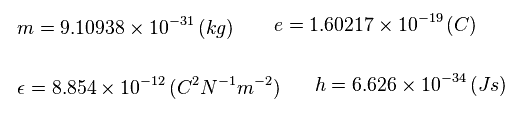
有効中心電荷 z は
(Sp.18)
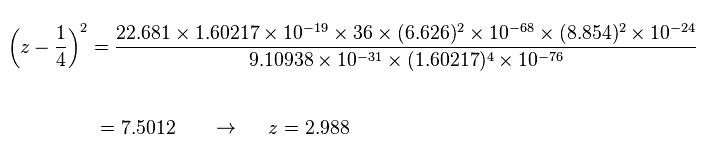
z = 2.988 と n = 3 を Sp.13 に代入すると、 半径 "r" は
(Sp.19)
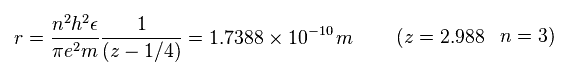

2014/2/24 updated This site is link free.