
(Fig.1) How do electrons and protons behave in touching things ?

What does trouching objects mean in atomic levels ?
Electrons and protons can attract each other through Coulomb force.
Then each electron and proton can be closer to each other limitlessly ? In fact, basic physics cannot answer even this simple question !
(Fig.2) Two conditions of Coulomb force and " ? " determine bond length !
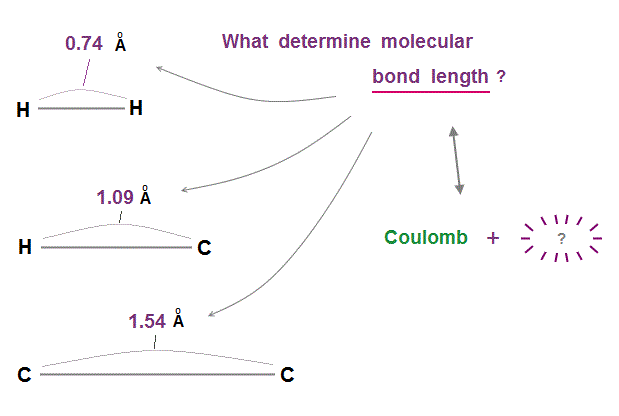
Molecular bond lengths are determined in each pair of atoms. Why two atoms cannot approach each other closer than the fixed bond length ?
If we consider only Coulomb force among electrons and nuclei, two atoms can be closer to each other limitlessly.
We need the second condition to keep two atoms from approaching each other. This is "de Broglie wavelength".
(Fig.3) de Broglie wavelength of hydrogen atoms determines bond length.
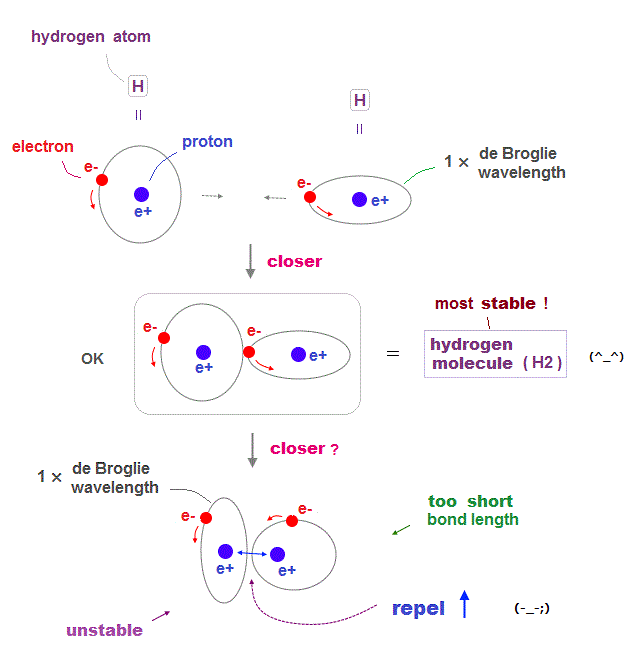
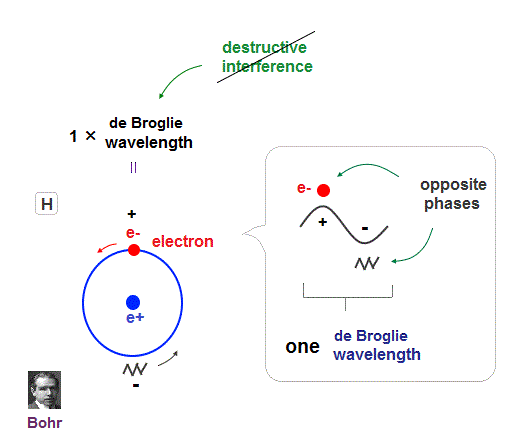
Quantum physics including Schrodinger equation and Bohr model is based on an integer times de Broglie wavelength of electrons to avoid destructive interference.
An electron in each hydrogen atom (= H ) has to keep 1 × de Broglie wavelength orbit, which is the reason two H atoms cannot approach each other limitlessly.
As two atoms are closer to each other, each electron tends to be attracted to another's positive nucleus, avoiding another electron, forming stable H2 molecule.
But if these two electrons try to be closer than the bond length, repulsive forces between two nuclei gets stronger, which prevents them from approaching.
Electron orbit has to keep 1 × de Broglie wavelength, electrons cannot stay longer in the narrower place between two nuclei to weaken the repulsion among protons.
(Fig.4) de Broglie wavelength smaller → bond length shorter →
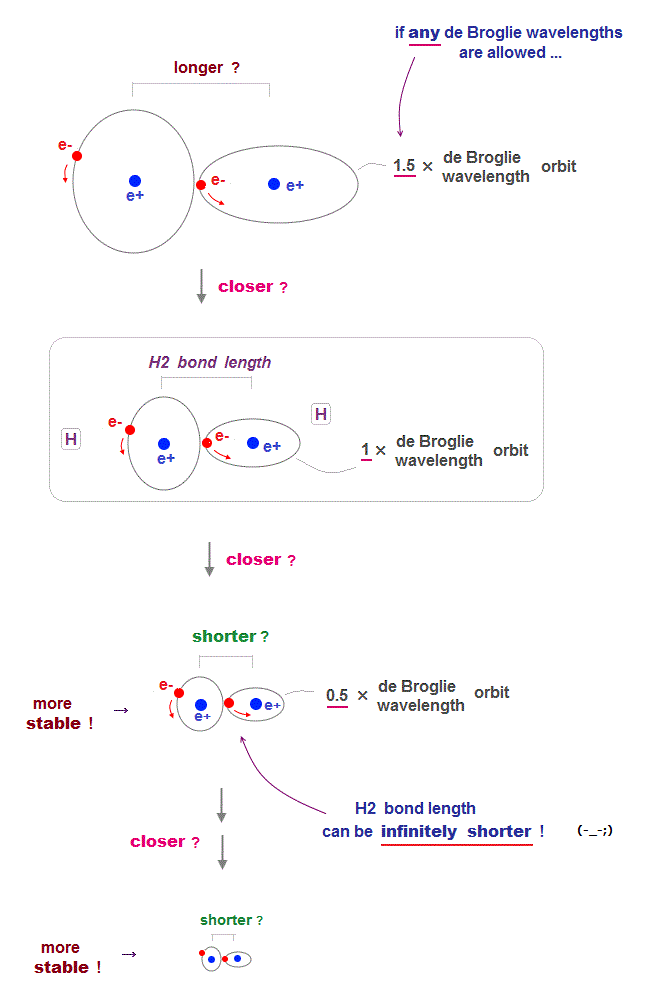
For each electron's orbit to keep 1 × de Broglie wavelength, two H atoms cannot approach each other limitlessly, which determines the molecular bond length.
If each orbit is allowed to have any de Broglie wavelengths ( including "non-integer" wavelength ), two atoms can be closer to each other limitlessly.
Because as two nuclei are closer to each other, electrons' orbit can be smaller (= de Broglie wavelength shorter ) to stay longer in narrower space between two nuclei to weaken their repulsion.
(Fig.5) are necessary to determine each molecular bond length.
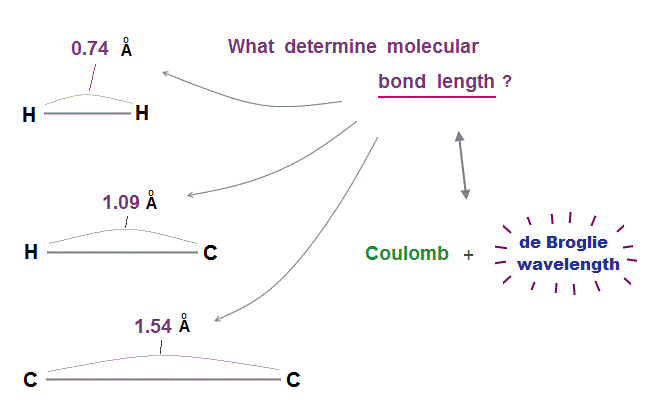
As I said, if each orbit can choose any de Broglie wavelengths ( including non-integer ), two atoms can approach each other limitlessly.
So two conditions of Coulomb force and an integer times de Broglie wavelengths are necessary to determine each molecular bond length !
Unrealistic electrons spin has nothing to do with molecular bonds.
(Fig.6) Quantum orbit satisfies an integer times de Broglie wavelength.
Only Coulomb force is insufficient to explain why atomic energy levels are quantized, and why an electron doesn't fall into nucleus.
Bohr model succeeded in getting actual atomic energies, proposing each orbit is an integer times de Broglie wavelength, as well as Schrodinger's hydrogen .
An integer multiple of de Broglie wavelength means an electron can avoid destructive interference and be stable.
Without this de Broglie wave, each electron can be attracted to positive nuclei, until they stick to each other and its energy is unlimitedly lower !
So the repulsive force by electron's de Broglie wave is strong enough to keep the electron away from the nucleus and cause Pauli exclusion force.
(Fig.7) Electron's de Broglie wave in Schrodinger' hydrogen is destroyed
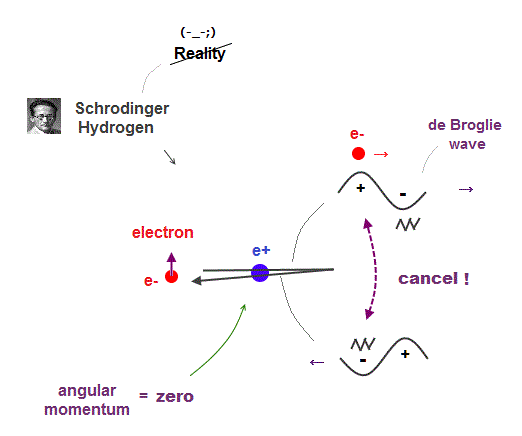
Electron de Broglie wave with experimental proof contradicts quantum mechanical atomic model.
Quantum mechanics claims that electrons in Hydrogen and Helium have zero orbital angular momentum, which means "linear-shaped" orbital.
If so, the opposie phases in electron's de Broglie wave always overlap and interfere with each other "destructively" (= cancel ).
As you see, zero angular momentum in quantum mechanical atoms is inconsistent with de Broglie theory, so false.
(Fig.8) Two orbits of H2 molecule avoid destructive wave interference
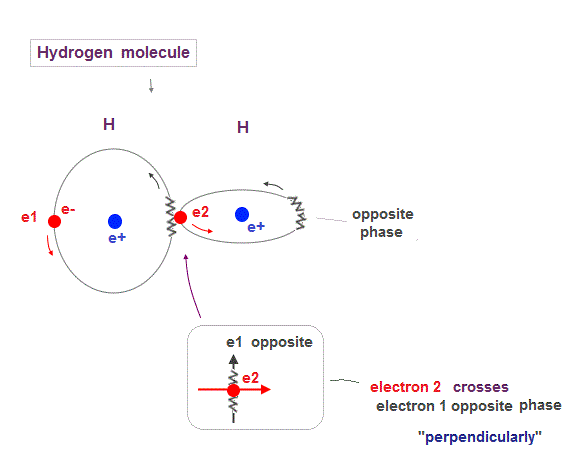
Like Helium atom, Hydrogen molecule (= H2 ) consists of two orbits of 1 × de Broglie wavelength.
So to avoid destructive interference, these two H2 orbits must cross each other "perpendicularly".
(Fig.9) Unreal spin is really involved in hydrogen molecule bond ?

Textbooks in quantum mechanics often argue that "up" and "down" spins form molecular bonds. But in fact it's physically impossible.
Because spin-spin magnetic interaction (= only 0.001 eV ) is too weak to cause any molecular bonds (= 3-4 eV ). So spin has nothing to do with molecular bonds !
(Fig.10) Point-like electron ( radius r → 0 ), rotation v → ∞

Angular momentum is given by mv × r ( v = velocity, r = radius ).
Electron spin also has angular momentum 1/2ħ, they claim
The problem is an electron is very tiny, point-like.
The point-like particle means its radius r is almost zero.
So to get the angular momentum 1/2ħ, the electron spinning must far exceed light speed ( this p.5, this )
So the electron spin lacks reality.
Even Pauli ridiculed the idea of "spinning electron".
But in "s" orbital of Schrodinger's hydrogen, this electron spin is the only generator of magnetic moment.
So they had no choice but to accept this strange spin ( Not as real spinning and speed ).
(Fig.11) Spin-spin magnetic energy (= 0.0001 eV ) vs. bond energy (= 4.5 eV )
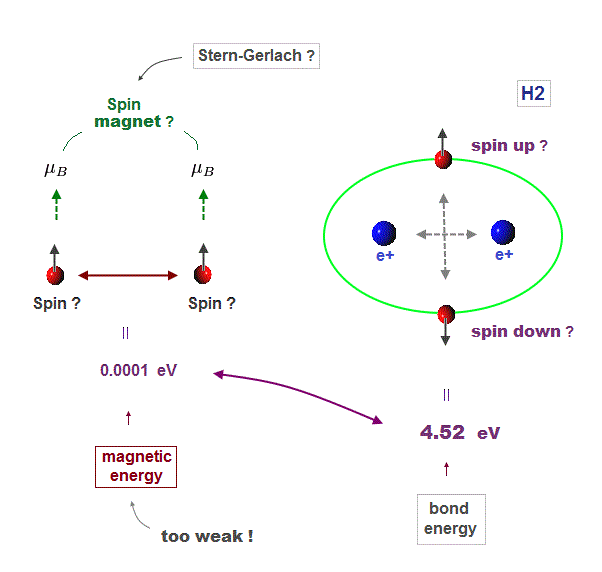
You may hear spin is tiny magnet with the magnitude of Bohr magneton.
We cannot see unreal spin itself, we just measure its magnetism by experiments.
We can replace unrealistic spin by real orbital motion causing the same magnetic field. "Spin" cannot explain actual phenomena.
Spin-spin magnetic interaction is too weak to explain actual ferromagnet.
See this p.7, this p.6. So spin model failed from the beginning.
Hydrogen molecular bond energy is known to be as large as 4.5 eV which electrons spin's magnetic energy (= only 0.0001 eV ! ) can NEVER reach.
(Fig.12) No solution → just "choose" trial functions ! = useless
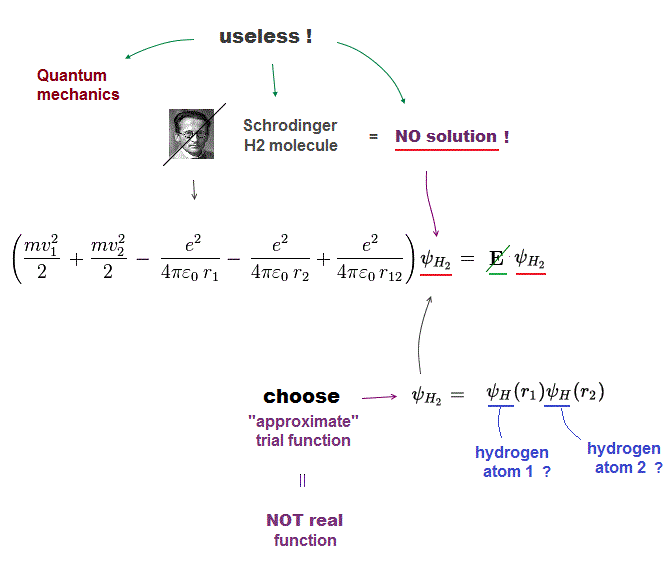
Schrodinger equation cannot solve multi-electron atoms and molecules. So all quantum mechanics can do is choose artifical trial function as "imaginary" solution.
"Choosing" convenient approximate function means quantum mechanics is useless and has no ability to predict any physical values.In case of unsolvable hydrogen molecule, we choose approximate function consisting of two H atoms. Of course, these are not true solutions.
(Fig.13) Each Coulomb term (= ①, ②, ③ ) must be independent !
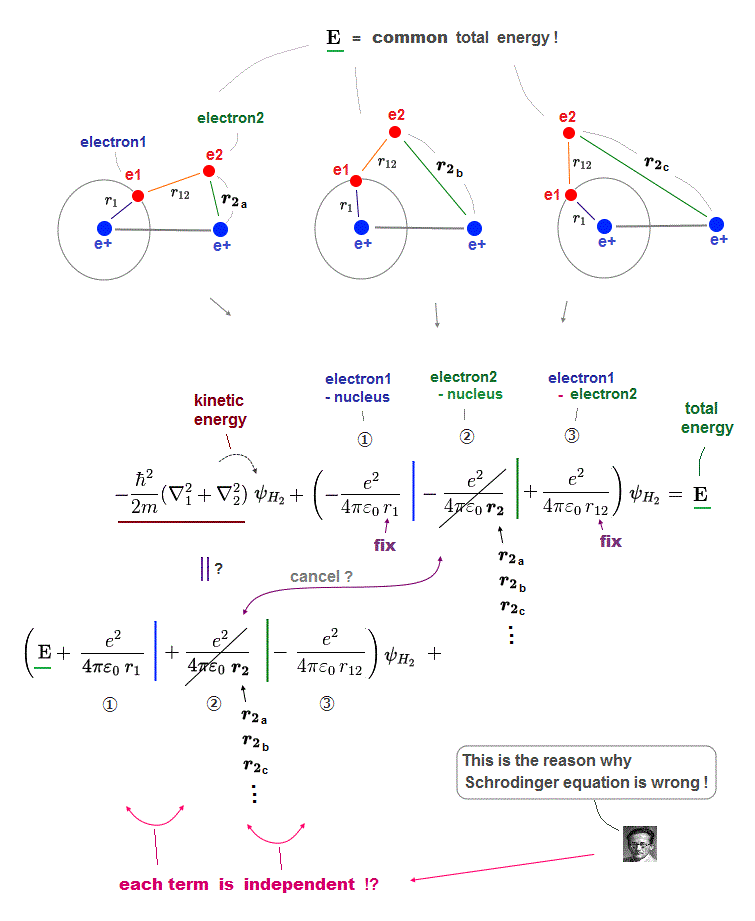
This page explains why Schrodinger's solutions can never be closer to true solution, no matter what approximate functions are tried in multi-electron atoms.
In Schrodinger wavefunction, each electron of H2 molecule can enter any place, which means any electron-nucleus electron-electron distances are allowed !
In Fig.13, we fix electron1-nucleus (=r1 ) and electron1-electron2 (= r12 ) distances, changing only electron2-nucleus distance (= r2 ).
For all these states to share the same common total energy E, only Coulomb term (= ② ) must be canceled out by its corresponding kinetic energy term independently.
In the same way, each Coulomb term (= ①, ②, ③ ) must be canceled out by its corresponding kinetic energy term independently from other Coulomb terms.
So each Coulomb term has nothing to do with each other, which cannot represent true molecules where each Coulomb term is closely dependent on each other.

2016/10/21 updated. Feel free to link to this site.