Home page
relativistic quantum field theory is unreal
QED cannot predict anomalous magnetic moment
Dirac unreal spin, Lamb shift
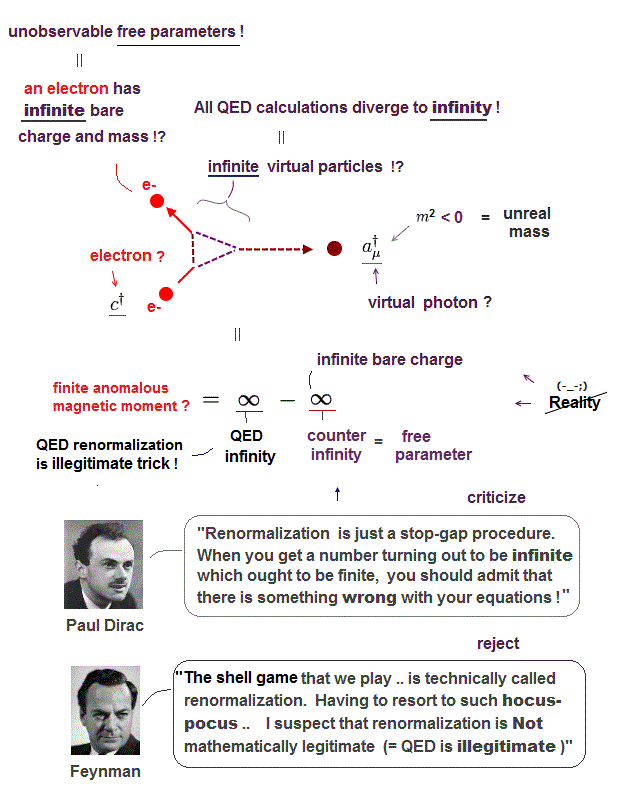
(Fig.1) QED is wrong, always giving useless infinities, unable to predict anything such as anomalous magnetic moment (= g-factor ).

Contrary to a lot of hypes, quantum electrodynamics (= QED ) is unsuccessful, useless, unable to predict any physical values such as anomalous magnetic moment (= electron's spin g-2 factor ) and Lamb shift.
According to the current unphysical quantum mechanics and relativistic QED, electromagnetic force is mediated by (unreal) virtual photons with imaginary mass moving faster than light, which paradoxically disobeys Einstein's mass-energy relation ( this-p.9-10, this-p.11 ).
Calculations of QED and the (unphysical) particle physics always diverge to meaningless infinities by these unreal infinite virtual particles ( this-p.10-11 ).
So QED has to remove these useless infinities by other artificially-created counter-infinities such as illusory infinite bare charge and mass ( this-p.4-5, this-p.14-upper, this-p.70-324, this-p.2-2nd-paragraph, this-p.4-2nd-paragraph ) in illegitimate renormalization to obtain some finite values such as electron's anomalous magnetic moment ( this-p.5-right ).
This-3rd~4th-paragraphs say
"Renormalisation refers to a term's ( artificial ) redefinition based on mathematical properties, which help eliminate infinity. A fundamental concept here is separating infinite from measurable finite physical variables. It is done by adding counter terms to the original Lagrangian of a given theory."
"The electron’s observed mass and charge are not the bare mass and charge in the original Lagrangian. They are "renormalised" values that take into account quantum corrections. The renormalisation method modifies these constants to fit experimental results (= artificial manipulation, Not QED prediction ), hence removing the infinite values ( this-p.18-last-paragraph )."
This QED's illegitimate removal of infinities by artificially redefining fictitious mass and change is call "mass or charge renormalization ( this-p.2 )".
This-p.1-right-2.2~p.2 says
"Unfortunately, QFT (= quantum field theory or QED ) was a complete failure since any attempted calculation under this theory resulted in an infinite number"
"Separation: separating an infinite series into two components, one that diverges to infinity and another that converges to a finite value. Eventually, the infinite component is ignored and only the finite part remains." ← illegitimate QED cannot predict any finite physical values.
"This technique of ignoring infinities is called renormalization. Feynman also recognized that this technique is not mathematically legitimate"
This-p.10-last and p.14 say
"Oppenheimer et al. calculated the first order
correction to 2 (= magnetic moment ) to be infinity"
"
Of course, this QED artificial math trick of infinity minus infinity giving some finite value is wrong, because in the right math, infinity minus infinity gives just uncertain indeterminate unphysical values that cannot define the definite anomalous magnetic moment nor Lamb shift values.
This is why even QED founders such as Dirac ( this-1st-paragraph ) and Feynman harshly criticized this QED illegitimate renormalization artificially removing infinities as "hocus-pocus", "dippy process", "inconsistent ( this-p.2-left, this-p.13-lower~p.14 )".
↑ QED is a completely-unsuccessful wrong theory unable to predict any physical values.
(Fig.2) QED calculations consist of unphysical virtual particle equations (= propagators ) always giving useless infinities.
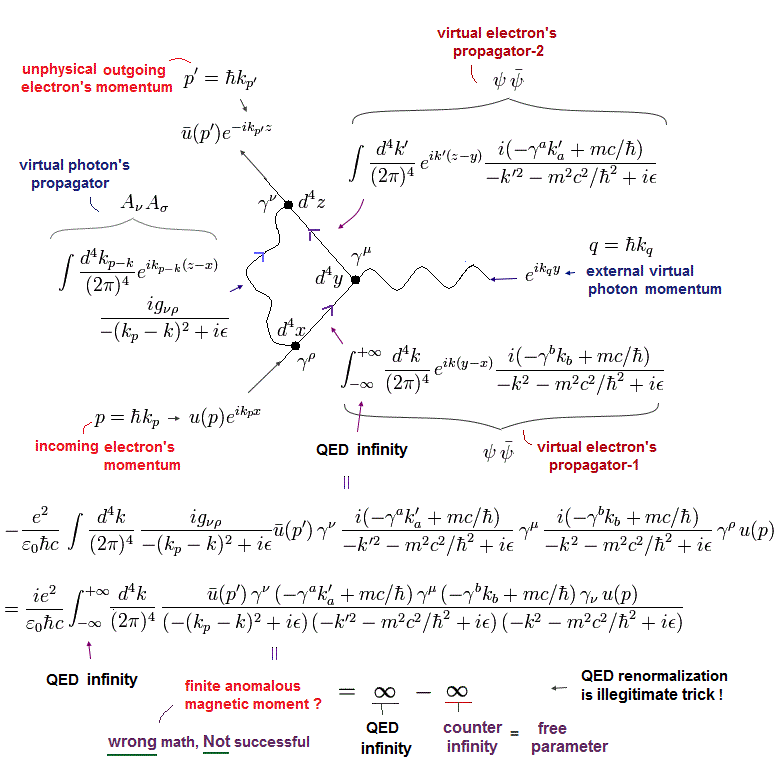
QED artificial calculations of the tiny electron's anomalous magnetic moment (= electron's g-2 factor ) use the simple, unrealistic interaction where an electron-1 (= p ) absorbs a (virtual) photon (= q ) to become an electron-2 (= p' ).
QED also says in this process, the electron-1 should split into (illusory) virtual electron-1 (= k ) and virtual photon (= p-k ), as shown in unphysical Feynman diagram.
QED must obey conservation of total energy and momentum satisfying equations of p + q = p' and k + q = k' (= all these p, q, p', k, k' represent relativistic energy and momentum of electrons and virtual particles, this-3rd-paragraph, this-p.25, this-p.6 ).
These unreal virtual electrons (= fermions ) and virtual photons forming one closed loop are expressed by unphysical equations called propagators ( this p.23 ) and gamma matrices (= γ this web site uses -1,1,1,1 notation ). this-p.8-9, this-p.3
↑ These virtual photons and electrons are known to disobey Einstein relativistic energy-mass relation called off-mass shell ( this-p.5-10, this-p.3, this-p.16-1st-paragraph ). ← The relativistic QED whose virtual particles violate Einstein relativity is self-contradictory and wrong.
To satisfy (paradoxical) Einstein relativity, these (unreal) virtual particles' energy must be infinite, which makes QED calculation always diverge to meaningless infinities by integration ( this-p.68-7.12 ).
QED just artificially separates and removes the unneeded infinite part (= actually including infinity + unneeded finite values ) by the artificial change of variables ( l = k + yq - zp ) by illegitimate renormalization to obtain the tiny finite anomalous magnetic moment value.
↑ They artificially remove only terms of γμ ( ... ) where γμ is unphysical gamma matrix.
But actually this term γμ ( ... ) illegitimately removed by renormalization is a freely-adjustable parameter that can be freely changed. ← We can freely change them between γμ-attached terms (= illegitimately removed by renormalization ) and non-γμ terms (= remain as the anomalous magnetic moment value ) by this formula. ← QED cannot predict anomalous magnetic moment.
Furthermore, in two-loop correction of anomalous magnetic moment, QED does Not remove even the part of γμ ( ... ) term ( this-Fig.5-new artificial L part surrounded by square contains γμ or γν, but not removed by renormalization ), which inconsistent artificial rule shows QED cannot predict anomalous magnetic moment.
They baselessly say the unphysical electron spin is expressed as (unphysical) σ matrices consisting of two γ matrices. ← This unphysical spin σ matrix including γ matrices is not removed by renormalization, which is also an inconsistent ad-hoc rule invalidating QED.
(Fig.3) QED artificial calculation lacks real particle or electron picture.
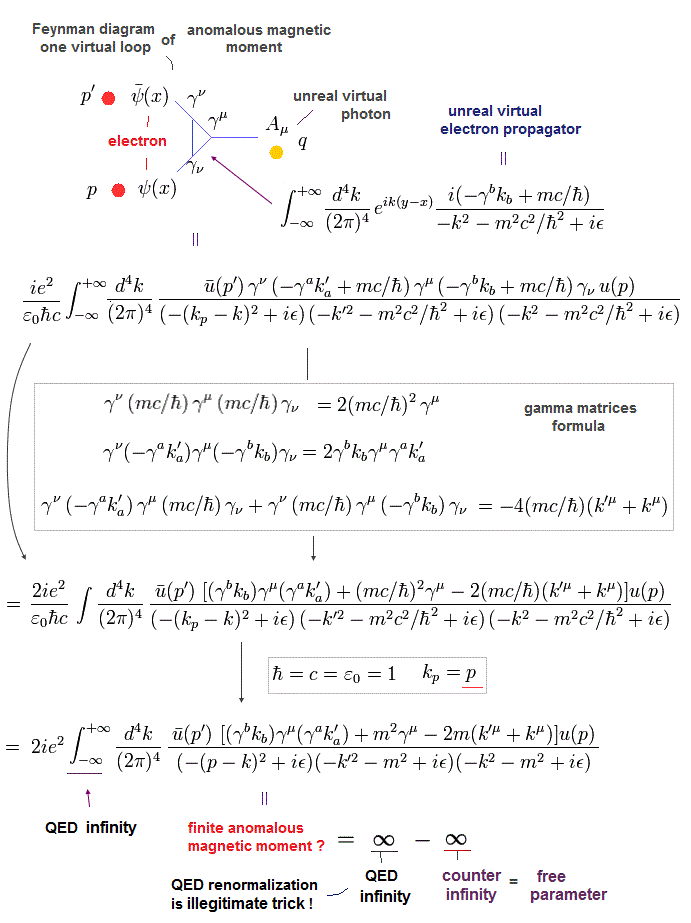
Using the unphysical γ matrix formula, QED one-loop anomalous magnetic moment equation becomes Fig.3 ( this-p.53-(5.10)(5.11), this-p.144, this-p.5-lower-4, this-p.2-4 ).
We use the relativistic notation of (-1 +1, +1, +1) version.
γk can be expressed by Feynman slash notation,
(Fig.4) QED uses artificial math transformation called Feynman parameter

QED artificially changes Fig.3 into Fig.4-lower using artificial math trick called Feynman parameter ( this-p.7(or p.5), this-p.53-(5.12), this-p.24-3.4~p.25 this-p.4-(15) ).
The denominator of the anomalous magnetic moment's equation is expressed using the new artificial variable l = k + yq - zp as [ l2 + Δ ]3 ( this-p.1-left ).
(Fig.5) QED artificial change of variables

Here we use the relativistic energy, momentum of an electron-1 (= p ), electron-2 (= p' ), a photon (= q ), and rest mass of an electron (= m ).
See this-p.35-(3.41)(3.42), this-p.6-(10)
The relativistic notation of this page is (-1,1,1,1) version.
(Fig.5') relativistic energy, momentum of electron (= p ), photon (= q )
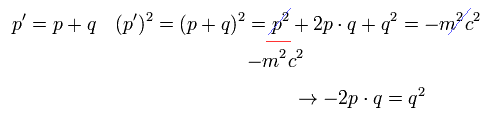
(Fig.6) QED uses artificial change of variables to manipulate anomalous magnetic moment value.
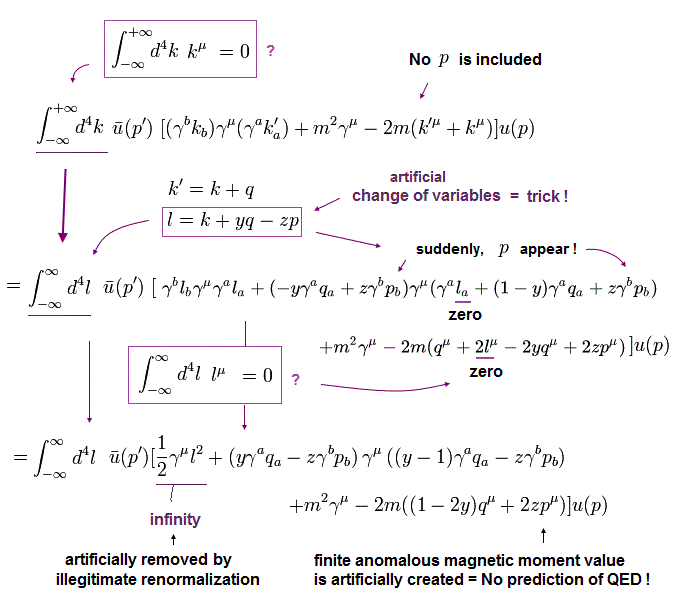
The numerator of QED anomalous magnetic moment's Fig.4-lower is changed into Fig.6-lower by using artificial change of variables of l = k + yq-zp to manipulate anomalous magnetic moment value, as shown on this page ( this-p.55-(5.22)-(5.24), this-p.145-(8.38),p.146-(8.43) ).
(Fig.7) QED anomalous magnetic moment math trick

Fig.6-lower equation of QED anomalous magnetic moment can be artificially changed into Fig.7 (= change from Eq.A to Eq.B ), as shown in this, using the math formula ( this-p.147, this-p.1-right ).
(Fig.8) QED artificial removal of unneeded terms to get unphysical spin anomalous magnetic moment

Using the QED unphysical electron spin relation expressed by unphysical γ matrices, Fig.7-lower-Eq.B can be changed into Fig.8-lower.
(Fig.9) QED unphysical spin = σ or γ matrices.
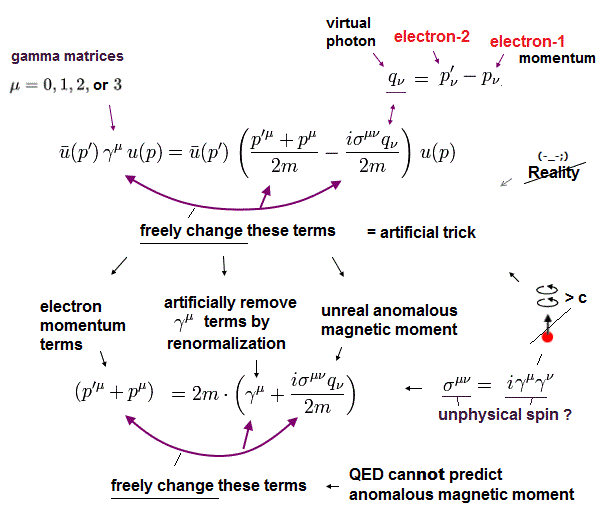
QED artificial math trick called Gordon identity can freely change the equation among γμ-matrix-terms (= removed by renormalization ), ( p' + p ) term, the unphysical spin σμ ν term ( this-p.35-4.11-p.36-1st-paragraph, this-p.1-(2), this-p.12-(46) ).
↑ Freely-changeable ( coefficient of ) spin σμ ν term (= anomalous magnetic moment value consisting of unphysical γ matrices, this-p.51-(5.3)(5.4),p.56-(5.26)(5.27) ) means QED has No ability to predict any physical values.
(Fig.10) ↓ This is Not physics but just artificial math irrelevant to real world.
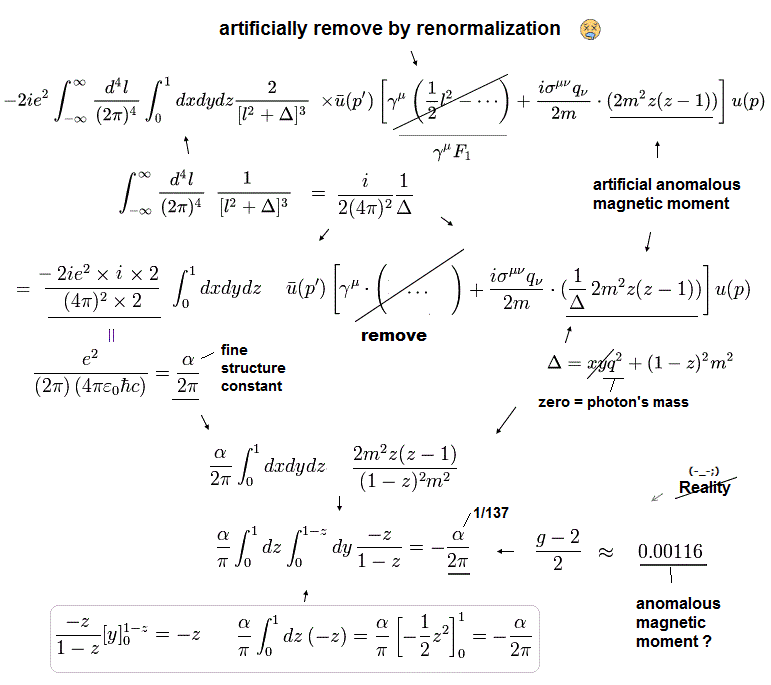
They use illegitimate renormalization to artificially remove or ignore the unneeded divergent terms proportional to γμ (= γμ F1, this-p.2-2nd-last-paragraph, this-p.7-2nd-paragraph, this-p.12-2nd-last-paragraph, this-p.36-2nd-paragraph-4.2, this-p.3-(12)(13)-charge renormalization, this-p.13-2.10, this-p.15-2nd-paragraph, this-p.4 ).
This-p.29(or p.21)-4th-paragraph says
"we.. have also ignored (= removed or renormalized ) all the terms that are
proportional to γμ, since they will only contribute to F1(q), to obtain a simplified
expression"
This-p.69(or p.65)-(7.36) says
"Since the first term (= γμF1 ) is.., it can be changed by renormalization. Indeed, this is again necessary
to remove an ultraviolet divergence ( this-p.56-(5.29) )"
By this illegitimate renormalization of the unneeded divergent terms proportional to γμ (= called F1 form factor, this-p.46-48 ), QED can get ( = artificially manipulate ) the one-loop correction of anomalous magnetic moment value = α/2π where α is fine structure constant, as shown in Fig.10-lower.
See this-p.1-4, this-p.147-151, this-p.15(or p.13)-p.21, this-p.59-(5.42)
Fig.10-2nd-equation (= Δ ) uses the formula of this-p.2-B.13
(Fig.11) QED can freely change the renormalization (= γμ matrix term ) and anomalous magnetic moment part (= σμν matrix ) with No ability to predict it.
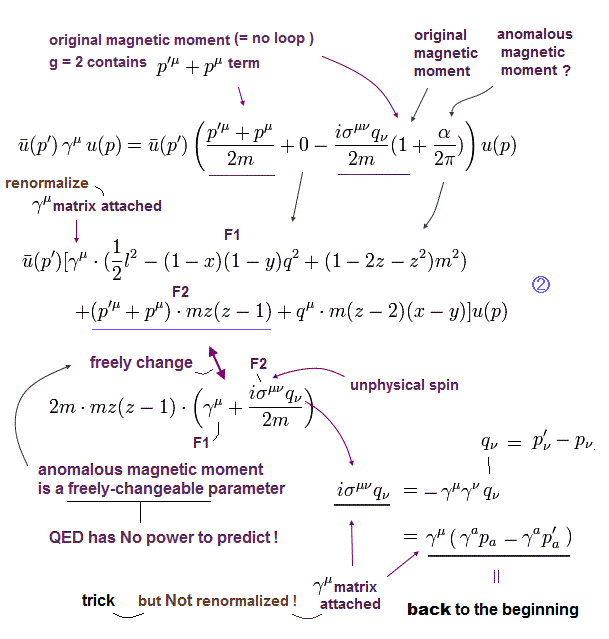
QED calculations always diverge to meaningless infinities.
So in the QED anomalous magnetic moment's one loop correction, they artificially divide the whole equation into the unneeded γμ term that must be removed (or ignored, this-p.2-2nd-last-paragraph ) by the illegitimate renormalization, and the unphysical spin's finite anomalous magnetic moment part (= σμν ).
QED can freely change the equation between coefficients of γμ matrix term (= removed by renormalization ) and anomalous magnetic moment part (= σμν matrix or p'μ + pμ term ) by this formula ( this-p.1-right-4~5th-paragraphs ).
This QED uses different inconsistent rules where getting the magnetic moment (= g/2 = 1 ) in Dirac equation transforms γμ terms into (p'μ + pμ) terms while getting anomalous magnetic moment (= (g-2)/2 = α/2π ) transforms (p'μ + pμ) into γμ terms. ← QED with inconsistent rules cannot predict magnetic moment.
↑ Actually, if they try to remove or renormalize terms proportional to γμ of Fig.7-the original Eq.A-1st equation ( instead of the later-changed Eq.B ), they can not get the desired anomalous magnetic moment value.
Furthermore, in QED anomalous magnetic moment's two-loop correction, unlike one-loop correction, they do Not remove part of the γμ term ( this-Fig.5 new artificial L surrounded by the square including γμ or γν is left as anomalous magnetic moment instead of being removed by renormalization ), which is an inconsistent rule.
As a result, QED just artificially manipulates anomalous magnetic moment value by various ad-hoc new rules separating terms and illegitimate renormalization.
(Fig.12) Original QED equation of Eq.A (instead of Eq.B ) gives unphysical infinite anomalous magnetic moment value, which means QED just artificially manipulates (= does Not predict ) anomalous magnetic moment value.

If we use the original Eq.A equation ( this-p.55(or p.49)-(5.24), this-p.18(or p.16)-upper or middle equations ) instead of Eq.B, the anomalous magnetic moment value (= after artificially removing terms proportional to γμ by renormalization ) unrealistically diverges to infinity.
↑ This shows QED is unable to predict anything, just artificially manipulating anomalous magnetic moment value.

Feel free to link to this site.