Home page
Einstein is wrong
Relativistic mc2 is wrong
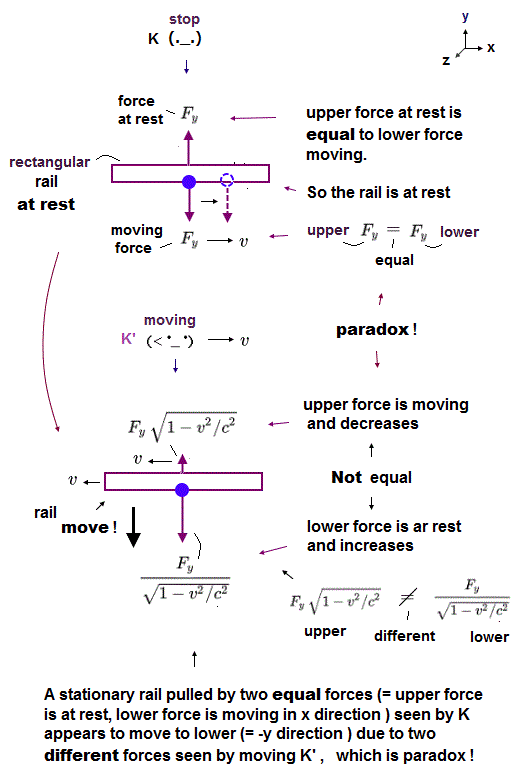
(Fig.1) A stationary rail seen by a stationary K is paradoxically moved as seen by a moving K' due to forces (= Fy ) changed as seen by K or K' observers.

In Fig.1, a rectangular rail is at rest as seen by a stationary observer K, because the force (= Fy ) upward (= stationary ) and the force downward (= moving in x direction at velocity of v by sliding along the lower rail ) acting on a rail is equal and balanced ( Fy = Fy ).
According to the paradoxical Einstein relativity, the force (= Fy or F⊥ ) in y direction (= ) appears to be weaker ( by Lorentz factor ) as seen by an observer moving in x direction relative to the force ( this-last, this p.14-p.15, this p.35 ).
So as seen by an observer K' moving at a velocity v in x direction, the upward force acting on the upper rail appears to be moving in -x direction and weaker than the original Fy, while the downward force acting on the lower rail appears to stop and be stronger than the original Fy, as shown in Fig.1-right.
↑ Two forces acting on the upper and lower parts of the rail are No longer equal only when seen by the moving K'.
As a result, the same rail at rest seen by K appears to be paradoxically moved downward as seen by the moving K', which is clearly a fatal paradox disproving Einstein relativity.
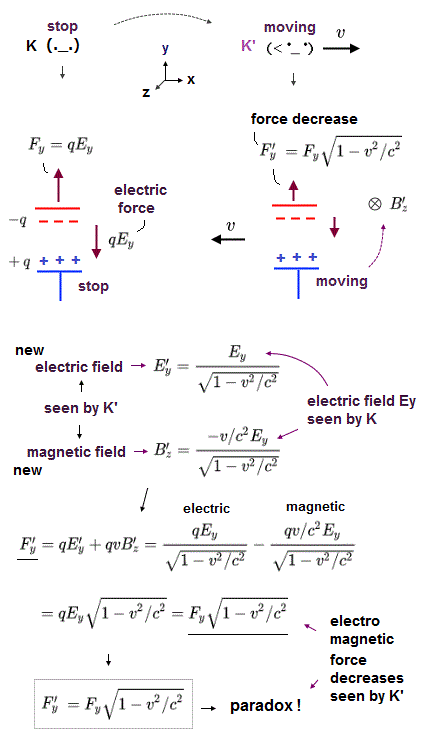
(Fig.2) Electric force seen by a stationary K appears to decrease as seen by a moving K' ?
The paradoxical force (= Fy ) changed as seen by different observers K and K' happens also in the (paradoxical) relativistic electromagnetic force.
Fig.2 shows the electric force (= qEy, q is charge, and Ey is electric field generated by the charges ) acting between two electrically-charged plates as seen by a stationary K.
According to (paradoxical) Lorentz transformation of electromagnetic field, the electric field E'y seen by K' is slightly stronger than Ey seen by K ( this p.14, this p.14 ).
But the whole charges appear to be moving in -x direction as seen by K' (= moving at a velocity v in x direction ), which causes new Lorentz magnetic force (= qvB'z ), which eventually weakens the whole force F'y like Fig.1, and the force paradox occurs.
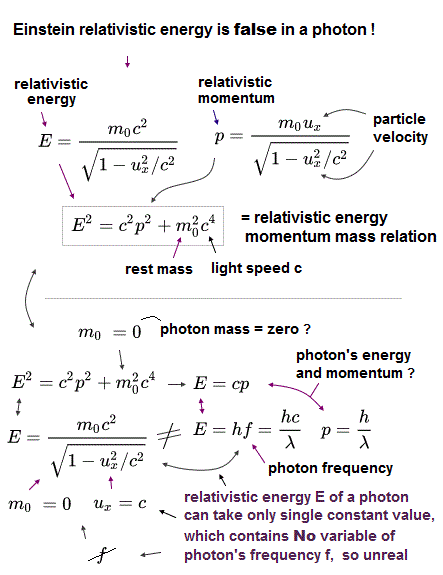
(Fig.3) Relativistic energy E relation consisting of mass m0 and velocity ux = c does Not include the variables of light frequency f nor wavelength λ, so it cannot express the photon's changeable energy depending on the light frequency f.
In fact, the paradoxical relativistic energy E and relativistic momentum p are incompatible with a (fictitious) photon or light energy.
A (fictitious) photon's rest mass (= m0 ) is said to be zero, and the photon's velocity ux should be always the light speed c (= which relativistic postulate is disproved by Sagnac effect, though ).
↑ So this relativistic energy E equation consisting only of the constant photon's rest mass m0 (= 0 ) and the constant light velocity c (= which can express only one fixed constant photon's energy ) does Not contain the variables of the light frequency f nor wavelength λ, hence, cannot explain the actual light (or photon ) energies changed by different frequencies or wavelengths.
As a result, the relativistic energy inconsistent with the photon or light energy is proven to be false.
(Fig.4) Force Fy acting on an object A moving at a velocity ux seen by a stationary K is changed into F'y seen by K' moving at a velocity v = ux (= K' is at rest relative to the object A )
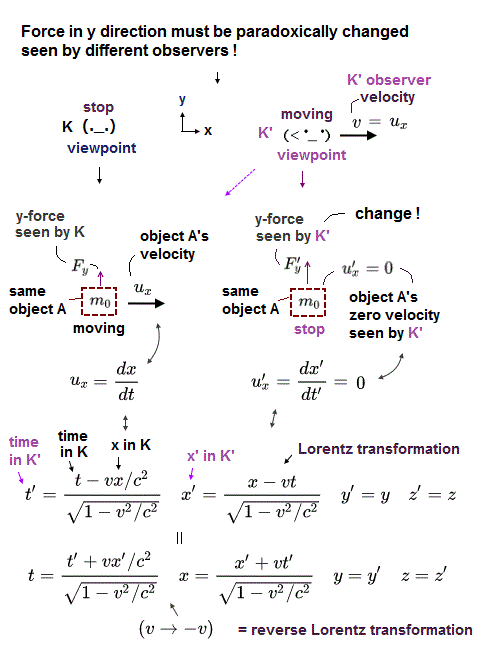
In Fig.4, the force Fy (= time derivative of relativistic momentum p ) acts on an object-A moving at a velocity of ux in x direction.
As seen by K' moving at the same velocity of v = ux as the object-A, the object-A appears to stop (= so A's velocity u'x seen by K' is zero ), and the force f'y paradoxically appears to increase seen by K'.
Here we derive this Lorentz transformation of force Fy changed from perspectives of K and K' by using Lorentz transformation and relativistic energy-momentum.
(Eq.1) Lorentz transformation and time derivative.
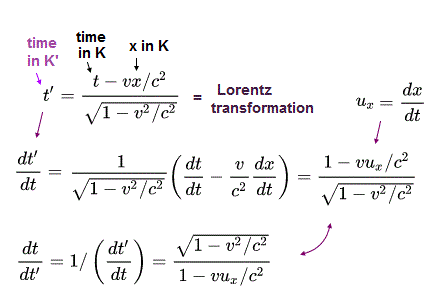
From the equation of Lorentz transformation, we can obtain the time derivative of the other coordinate's time such as dt'/dt and dt/dt' where t is the time measured in K frame, and t' is the time measured in K' frame.
An object's velocity in x direction seen by K is expressed as ux = dx/dt where x is x-coordinate seen by K.
(Eq.2) ux' is an object's velocity in x direction seen by K', and ux is an object's velocity seen by K
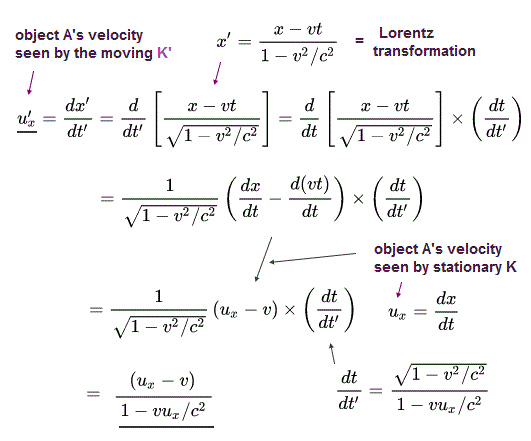
An object A's velocity in x direction seen by the moving K' observer is defined as u'x = dx'/dt' where x' t' are the space and time measured in the moving K' frame.
In the same way, an object A's velocity in x direction seen by the moving K observer is defined as ux = dx/dt where x, t are the space and time measured in the stationary K frame.
Using Eq.1, we can obtain Lorentz transformation of an object's velocity ( u → u'x ) as shown above.
(Eq.3) Lorentz transformation of an object's velocity in y direction between the velocity u'y seen by K' and velocity uy seen by K
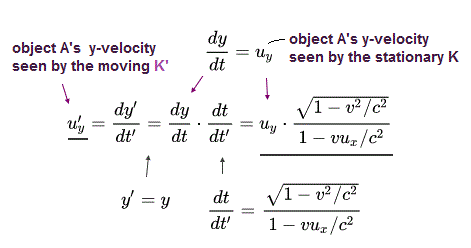
In the same way, using the relation of Eq.1, we can obtain Lorentz transformation between an object's velocity in y direction seen by K' (= u'y ) and seen by K (= uy ), as shown above.
K' observer is moving in x direction, so y-coordinates seen by K and K' are the same y = y'.
(Eq.4) An object A's acceleration in x direction seen by K' (= du'x/dt' ) and seen by K (= dux/dt )
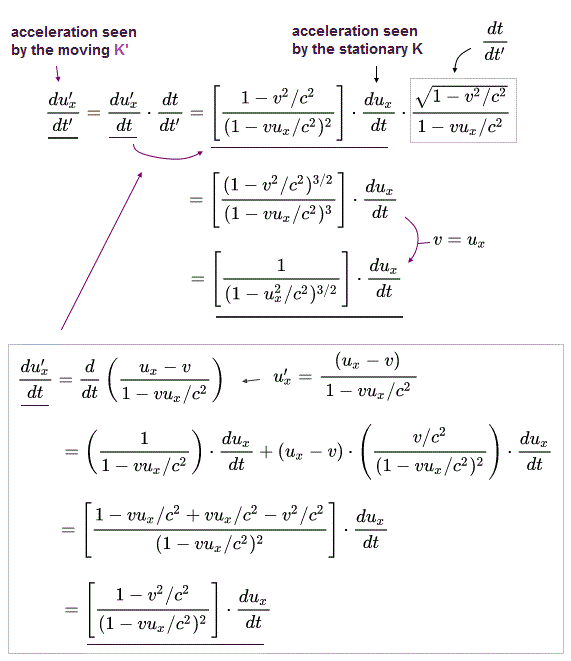
Acceleration is defined as the time derivative of an object A's velocity.
Using Eq.1 and Eq.2, we can obtain the relation (= Lorentz transformation of acceleration ) between the object A's acceleration in x direction seen by the moving K' observer (= du'x/dt' This K' observer is moving at the same speed v = ux as this object at this point, so u'x = 0 ), and an object's acceleration in x direction seen by the stationary K (= dux/dt ).
(Eq.5) Force (= Fx ) equals the time derivative of an object's momentum p

Force in x direction (= Fx ) is defined as the time derivative of an object's (relativistic) momentum p in x direction ( Fx = dpx/dt ).
So we can obtain the upper equation of force (= Fx ) in x direction in K frame or seen by K ( this p.46 )
(Eq.6) Force acting on an object A in x direction is the same seen by K (= Fx ) and K' (= F'x ), Fx = F'x

In the same way, the force acting on an object A in x direction seen by the moving K' (= F'x ) becomes like the upper figure.
This object A appears to stop seen by the observer K' moving at the same speed as the object, so the object A's velocity is zero u'x = 0 seen by K'
From Eq.5 and Eq.6, we can know that forces acting on an object in x direction does Not change seen by the stationary K (= Fx ) or seen by the moving K' (= F'x ). Fx = F'x = F|| ( this last, this p.15, this last )
It means the force in the x direction (= parallel to the observer K's moving direction) is unchanged both in K and K' frames under Lorentz transformation.
(Eq.7) Lorentz transformation of acceleration of the object A in y direction seen by K' (= du'y/dt' ) and seen by K (= duy/dt )

Using Eq.3 and Eq.1, we can obtain Lorentz transformation of the acceleration of an object A as seen by the K' moving at the same speed (= v = ux ) as the object A, and as seen by the stationary K ( this p.22 ).
The object A is moving at a velocity ux in x direction (= so velocity in y direction is zero, uy = 0 ) seen by the stationary K, This object A appears to stop seen by the K' observer moving at the same speed (= temporarily, v = ux ) as the object A.
(Eq.8)
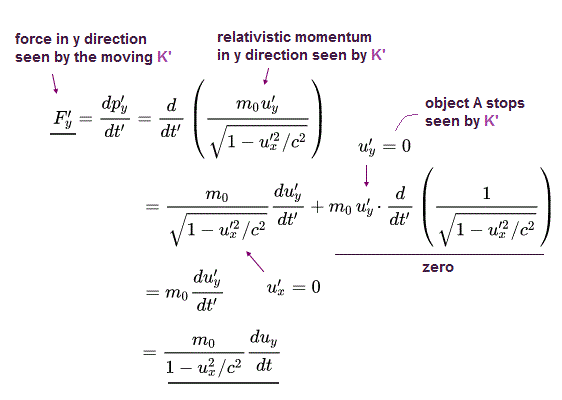
Force is defined as the time derivative of the object's relativistic momentum p.
Using Eq.7, we can obtain the equation above in this situation.
(Eq.9) Force in y direction, which is moving in x direction seen by the stationary K (= Fy ), appears to be smaller than the force in y direction (= F'y ), which stops seen by the K' observer moving at the same speed in x direction as the object A and its force ( Fy < F'y )

From Eq.8, we can conclude that the moving force in y direction (= Fy ) acting on a moving object A seen by the stationary K appears to be weaker than the force in y direction acting on a stationary object A in y direction (= F'y or F'⊥ ) seen by the K' moving in x direction at the same speed as this object A ( this last, this p.15, this last ).
So the force in y direction (= perpendicular to Lorentz boost direction of K' observer ) acting on the same object appears to increase or decrease depending on the differently-moving observers, which relativistic force causes serious paradox.

Feel free to link to this site.