
Home page
Relativistic QED is false.
Quantum field theory is unreal.
Particle physics experiment
(Fig.1) Today's particle physics can only describe illusory W boson, quarks, left-handed electrons as unphysical math irrelevant to real world's phenomena.

Today's particle physics based on standard model is useless, dealing only with unreal particles described as unphysical math symbols or equations lacking real particle shapes ( this-p.5-25, this-p.6~p.28, this-p.2~p.47 ), just wasting money in meaningless gigantic colliders.
According to this mainstream particle physics (= based on Weinberg unphysical electroweak theory ), fictional unseen quarks with fractional-charges of a neutron decay into a proton and the illusory extremely-heavy W boson (= unobservable ), and then the left-handed electron and unseen neutrino (= expressed only as unphysical matrix ) in the fictitious weak interaction.
↑ This illusory W boson (= emitted from a neutron or a proton ) is said to be 80 times heavier than a proton or a neutron, which clearly violates the mass or energy conservation law (= one neutron decays into 80 times neutrons or W boson ).
So today's unphysical particle physics illogically says this W boson is just an unreal virtual particle disobeying Einstein relativistic mass-energy relation ( this-p.6-left ) called off mass shell ( this-p.8-left, this-p.6 ).
↑ All these illusory unstable unseen quarks, W boson are expressed only as unphysical math symbols lacking real particle picture in today's useless particle physics.
(Fig.2) Today's standard model = Glashow-Weinberg-Salam theory lacks real particle picture in illusory W, Z bosons, photon, unphysical mixing angle θ

Today's particle physics or standard model based on Glashow-Weinberg-Salam (= GWS ) theory lacks reality, just describing illusory particles such as W,Z bosons and photons as unphysical math symbols with No concrete shapes ( this-p.14, this-p.55 ).
The illusory virtual W bosons with ± charges violating mass-energy conservation law are said to mediate the (fictional) weak force in beta-decay of a neutron and a proton. The illusory (virtual) Z bosons with neutral charge are also said to mediate the weak interaction between (unseen) neutrinos (= ν ) and other particles ( this-p.2-6 ) by disobeying the relativistic mass-energy relation ( this-p.2 ).
This unphysical GWS theory introduced the unphysical concept called weak mixing (Weinberg) angle θW artificially linking these illusory W, Z bosons and photons ( this-p.3 ).
The left-handed electron (= directions of spin S and momentum P are opposite ) and (unseen) quarks interacting with W boson was inferred from experiments measuring the direction in which electrons flied under magnetic field (= electron spin is unreal, unseen ) in beta decay ( this-p.3, this-p.5-6, this-p.4 ).
↑ This standard model based only on the left-handed particles ( this-p.18, this-p.7-(3.10), this-3rd-paragraph, this-p.4-10 ) contradicts Einstein relativity where the left-handed particles become right-handed as seen by different observers.
(Fig.3) Particle colliders' detection efficiency of lights (= photons ) and electrons into which illusory unstable particles decay is too low to confirm standard model's prediction.
This particle physics or standard model is useless, unable to predict anything, consisting of many freely-adjustable parameters, and illusory particles (= useless short-lived W,Z,Higgs bosons, unseen quarks, composite particles.. ) which is too short-lived to observe ( this-p.4-last ).
↑ Masses of all these illusory particles such as Z, Higgs bosons and interaction coupling strength such as g and g' are freely-chosen parameters which can Not be predicted by today's particle physics, standard model or GWS theory ( this-p.66-68, this-p.13 ).
By using artificial wrong definition or unrealistic theory ( this-p.5-3.4~p.6-left ), they say this standard model can predict only the (illusory) W boson's mass ( this-11th-paragraph ) and the (unphysical) Weinberg (= weak mixing ) angle θW.
But all the (dubious) experiments of today's particle physics rely on very unreliable data, calorimeters and detectors of final products such as photons (= lights ) and electrons, which detection efficiency is too low, far less than 100%, which can Not measure or prove the (illusory) W boson's mass.
Physicists have to guess masses of such illusory short-lived unobservable W,Z and Higgs bosons by measuring all energies of final products such as lights (= photons ) into which the W,Z,Higgs bosons are said to decay ( this-p.14-16 ).
↑ But measuring all energies of these final products is impossible, because photodetectors' detection efficiency (= called quantum efficiency ) in particle colliders is far lower than 100% (= more than 70% of lights or photons' energies are undetectable, this-p.3,p.4,p.14 ).
This-p.14-last-paragraph (or this-p.15-last ) says
"The quantum efficiency depends on the type of photodetector used to detect the scintillation
light, which is typically ∼15–30% (= more than 70% of all energies are lost, undetectable ) for photomultiplier tubes and ∼70% for silicon photodetectors for
visible wavelengths (= only visible lights can be detected. all other lights such as X-ray, γ rays, infrared lights are lost, undetectable ). The quantum efficiency of the detector is usually highly wavelength dependent"
↑ The energies of almost all lights with almost all wavelengths (= except some visible lights ) are undetectable, invisible (= high-energy γ rays, X-rays, and low-energy infrared lights are undetectable by photodetectors that also cannot detect charged particles, this or this-p.57-Fig.5.19 ).
This or this-p.10-iii), p.18-2nd-last-paragraph say
"Only a fraction of the photon reach the photocathode. The rest is either absorbed inside crystal"
"In a sampling calorimeter, most of the soft slower electrons will Not contribute to the signal"
Furthermore, almost 40% energies disappear undetected (as heat ) by colliding with nuclei or emitting unseen neutrinos ( this-p.53, this-p.27-2nd-paragraph ).
Particles inside colliders lose their energies in scintillators (= calorimeters ).
This-overview-2nd~4th-paragraphs say ↓
"After the passage of a particle, many of the atoms in the scintillating medium will be excited into higher energy levels. Most of the excitation energy is converted into heat and vibrations of the lattice (= undetectable energies ).
"Some of the energy is released as light, which cannot be absorbed by the medium.
The scintillation efficiency is defined as the fraction of the deposited energy that appears as light. The efficiency for even the best scintillators is low, 7 percent for sodium iodide crystals doped with thallium, and 3.5 percent for the best organic material (= the remaining 93~96% energies are undetectable, missing )"
↑ As a result, the precise measurement of the masses (= energies) of the (illusory) W,Z,Higgs bosons (and unreal quarks, composite particles ) are impossible (= so No experimental evidence that these illusory too-short-lived useless particles exist ), hence, even the standard model's only prediction of W boson's mass (= energy ) is wrong, impossible, contrary to hypes.
The measurement of the unphysical Weinberg (= weak mixing ) angle θW depends on artificial (= baseless ) definition measuring the unseen, elusive neutrino scattering allegedly producing (illusory) Z boson (= neutral current ), which experiments are unreliable due to impossibility of detecting the ghost-like unseen neutrinos ( this-p.17-18, this-p.17-last-paragraph ).
This-p.17-2nd-paragrpah says
" This result by the HPWF group,.. was in fact inconsistent with the
predictions of the GWS (= Glashow-Weinberg-Slam ) model. However, this negative published result
was largely ignored."
This-p.18-2nd-paragraph says
"Furthermore, the Weinberg
mixing angle that was determined from R and Rbar in the early 1970s was 0.38; it now is
0.23. Prima facie, this sheds significant doubt on the accuracy of the
results in 1973/4 ( this-p.18 )"
As a result, the present particle physics or standard model is useless, unsuccessful, unable to predict any physical values, just wasting taxpayers' money, contrary to hypes.
(Fig.4) Higgs boson is just an unphysical math theory lacking real particle picture.
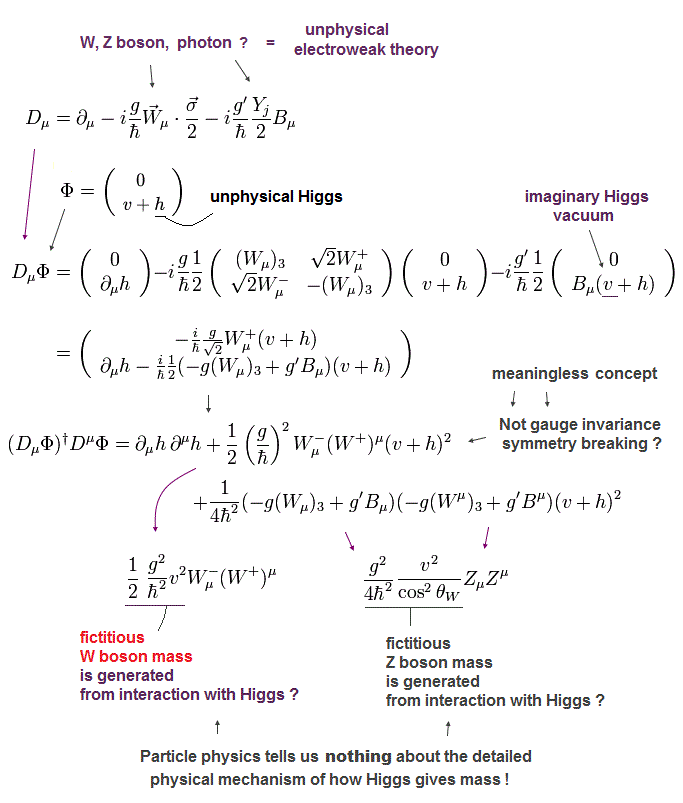
The Higgs boson is said to give mass to (illusory) particles such as W,Z bosons, electrons, quarks.
But in fact, the (illusory, too unstable) Higgs boson allegedly found inside large hadron collider (= LHC ) is useless, unable to give masses to other particles.
The still-unfound (illusory) Higgs field allegedly filling space like the ether is said to give mass ( this-3rd~4th-paragraph ).
But today's useless particle physics or standard model, which just presents unphysical abstract math relation, can Not show any detailed mechanism of how this (illusory) Higgs field gives masses to other particles. The Higgs boson is also expressed only as a unphysical math symbol "h" ( this-p.8, this-p.9, this-p.7-9, this-p.5-7 ) lacking real particle picture.
(Fig.5) Today's particle physics calculations are useless, giving only meaningless infinite values, which cannot predict any physical values.
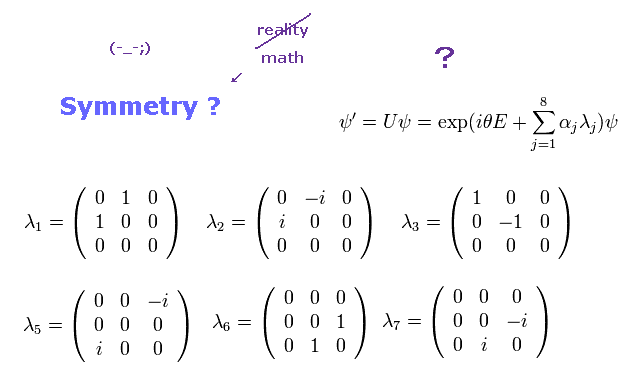
First of all, the reason why these (illusory) W,Z bosons need Higgs as a source of mass is unrealistic.
All calculations of the relativistic quantum field theory, QED and particle physics are known to give only meaningless infinities, which must be artificially removed by illegitimate renormalization ( this-1st-paragraph ).
If the illusory W or Z boson has mass or mass term in their unphysical abstract equation, this calculations always diverge to useless infinities that cannot be removed nor renormalized ( this-p.23-24, this-p.7-upper, this-p.23(or o,22 ), this-p.3-last ).
↑ So just to artificially remove the unphysical infinities by illegitimate renormalization, these (illusory) W,Z bosons and electrons are said to be massless, needing Higgs field as a source of (virtual) masses ( this-p.5-lower ).
In addition to this unrealistic infinities or renormalization, the particle physics relies on the unphysical gauge (or phase ) transformation symmetry (= No physical meaning, this-p.1-last, this-p.1-first-paragraph ).
To satisfy this artificial unreal gauge symmetry or invariance (= their abstract equation is unchanged by this unphysical gauge transformation ), the W,Z bosons must be massless, and the interaction with Higgs must be the only source of their masses as "contradictory spontaneous symmetry breaking ( this-p.4-5, this-p.23-24 )".
↑ Standard model must satisfy the unphysical gauge symmetry, but this symmetry must be broken by Higgs after all, which is contradictory.
This-p.2 says
"Gauge symmetries: "purely formal" (Healey), No physical
instantiations."
As a result, today's useless particle physics based on Higgs boson can Not show any legitimate reason why such (illusory) particles need to be massless, relying on unphysical Higgs mechanism, fictitious gauge, meaningless infinity renormalization for obtaining masses.
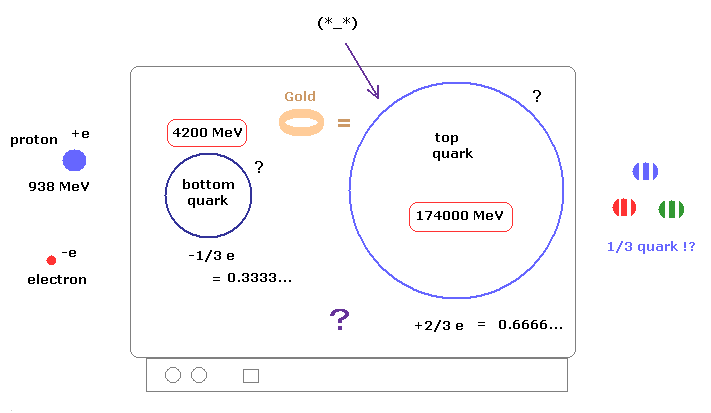
(Fig.6) Unseen quarks with unreal fractional charges are expressed only as unphysical math matrix ?
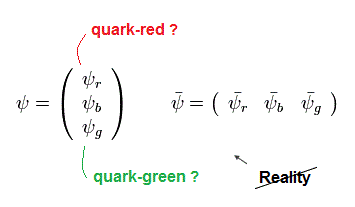
Today's useless particle physics or standard model can only describe the unseen (illusory) quarks with fractional charges and (illusory ) gluons mediating nuclear strong force proposed by Gell-Mann as unphysical math symbols or meaningless matrix ( this-p.3, this-p.7 ).
The particle physics or standard model is based on the fictional concept called gauge or gauge symmetry.
These illusory quarks are said to satisfy this unphysical gauge symmetry called SU3 symmetry (= the quark equation using unphysical matrix is unchanged by the fictional gauge transformation, this-p.8-9 ), which is irrelevant to real world.
As a result, today's particle physics based on standard model or GWS theory is useless, unreal, unable to predict anything.
The fractional-charge quarks can Not be isolated nor confirmed, so No evidence that such unobservable quarks really exist.
But the current illogical particle physics baselessly claims the observation of electrons and unseen neutrinos scattered by protons may suggest the existence of the (unseen) quarks.
They first insisted each proton or neutron consists of three valence quarks.
↑ But this first simple three-quark model failed to explain experimental results, so they paradoxically started to say each proton or neutron consists of many (unreal) virtual sea quarks ( this-p.5, this-p.7 this-p.7-8 ).
As a result, there is No reliable evidence that such ad-hoc quarks with fractional charges exist.
It is known that today's unphysical quantum electrodynamics (= QED ) failed to explain any nuclear or quarks' energies or physical values.
So physicists have to rely on artificially-chosen parameters and models called quantum chromodynamics (= QCD ) that also can Not predict any nuclear or quarks' physical values.
In this alleged first-principle calculations (= QCD ) of hadrons (= nuclei, pions, quarks.. ), this research paper ↓
p.1-right-2nd-paragraph says "a parametrization including qq¯,.. qqgg¯ (= quark q, gluon g ) components was fitted to reproduce experimental data on the (unstable, unseen) pion parton distribution functions" ← No theoretical prediction
p.2-right-lower and p.4-Table I used artificially-created models and freely-adjustable parameters such as quark, gluon's masses with No QCD prediction.
p.3-left shows this quantum field theory or QCD can express (fictional) quarks and gluons only as nonphysical math symbols with No real particle shape.
↑ As shown here, the present quantum field theory or quantum chromodynamics (= QCD ) describing the unseen quarks and gluons by the unphysical math operators and free parameters, models, can Not predict any nuclear, pion, quark's physical values.
The 4th paragraph of this hyped news (6/13/2025) say
"Modeling these functions is difficult due to their complexity and limited availability of experimental data. However, AI and ML offer new ways to analyze and understand these complex functions by processing large sets of data gathered by collider facilities." ← based on experimental data, Not on quantum theoretical prediction.
↑ This research paper used freely-adjustable parameters and artificial models for nuclear (unseen) quarks and gluons ( this-p.10-11, this-p.2-2nd-paragraph ) instead of QCD predicting them
Top quarks are illusion, unisolable, too short-lived to observe directly ( this-6th-paragraph ), too rare to distinguish from other irrelevant backgrounds (= only one top quark is said to appear in trillions of protons' collisions, this-8th-paragraph )
But the 2nd paragraph of this recent hyped news (7/8/2025) says
"suggests that top quarks—the heaviest and shortest-lived of all the elementary particles—can momentarily pair up with their antimatter counterparts to produce a "quasi-bound-state" called toponium. Further input based on complex theoretical calculations of the strong nuclear force—called quantum chromodynamics (QCD)—will enable physicists to understand the true nature of this elusive dance." ← wrong
↑ This research paper ↓
p.15-2nd-paragraph says "Modelling uncertainties are taken into account for 𝑡𝑡¯ (= top quark ) quasi-bound-state production. They are applied to both the main model as well as the simplified model." ← QCD or quarks are fiction based on artificial modelling.
p.17-9.1-1st-paragraph says "Systematic uncertainties,.. ( unknown ) nuisance parameters"
p.18-last~p.19 says "Apart from the dominant statistical uncertainties, the measurement precision is limited by signal and background modelling uncertainties." ← the present particle collider's detectors' detection efficiencies are too bad to precisely measure the (illusory top quark) particles' mass or energies.
p.23-1st-paragraph says "The cross-section of the quasi-bound-state contributions is a free parameter in the fit with the extended model."
↑ The present quantum chromodynamics (= QCD ) heavily depends on artificially-chosen models and free parameters, so can Not predict nor validate any phenomena such as top quarks, contrary to hypes.
The 3rd paragraph of this hyped news (7/11/2025) says
"The first process under study was the Higgs-boson decay into a pair of muons (H→μμ)."
↑ This research paper-p.6-4th-paragraph says ↓
"Systematic uncertainties in the signal modeling arise from both theory and experimental sources, and are incorporated into the signal-extraction fit via nuisance (= freely-adjustable ) parameters "
↑ Particle physics relying on freely-chosen models and parameters can Not predict or validate Higgs.

Feel free to link to this site.