Home page
Dirac's hydrogen is wrong.
QED is wrong.
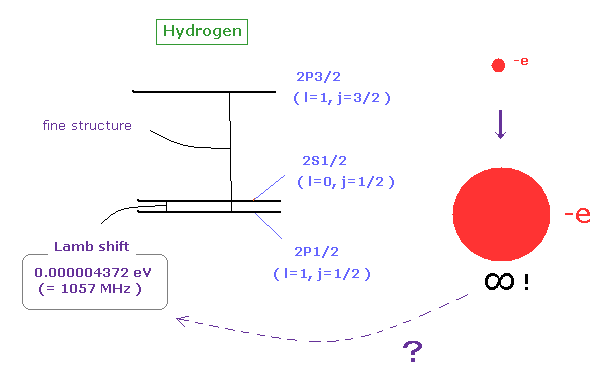
(Fig.1) QED just gives meaningless infinities, which cannot predict any physical values such as tiny Lamb shift energy splitting.

After the realistic Bohr-Sommerfeld model successfully predicted fine structure energy splitting between 2p1/2 and 2p3/2 without using the unreal electron spin, the unphysical quantum mechanical Dirac equation accidentally obtained the same fine structure energy solution as the Bohr-Sommerfeld model ( this-p.14, this-lower ).
It is said that there is a negligibly tiny (= useless ) energy splitting (= just 0.00000437 eV ) between ( unseen, imaginary ) 2s1/2 and 2p1/2 energy levels called Lamb shift, which is as small as unspecific thermal fluctuation, electron's orbital tiny precession. nuclear spin's hyperfine, and other fine structure (= 3d5/2-3p3/2 → 2 )...
↑ This negligibly-tiny useless Lamb shift does Not need the (illusory) 2s1/2 or the unreal QED virtual particles ( this-7th~8th-paragraphs, this-p.2-4th-paragraph ).
Relativistic quantum field theory and quantum electrodynamics (= QED ) are useless, unphysical, always giving meaningless infinities, which cannot predict any physical values such as Lamb shift and anomalous magnetic moment.
These QED meaningless infinities allegedly caused by (unreal) infinite virtual particles with imaginary mass (= disagreeing with Einstein mass energy relation, this-p.9-10, this-p.3 ) must be artificially removed by illegitimate renormalization ( this-middle~lower ).
This QED illegitimate math trick or renormalization artificially ignoring infinities is harshly criticized even by founders of QED as "hocus-pocus" or "illegitimate ( this-1st-paragraph, this-p.13-lower )".
This-p.4-2nd and 4th-paragraphs say
"Weinberg uses a fictitious photon mass in
the photon propagator which leads to a high and low-energy term. When added, the
fictitious mass cancels, yielding a constant and the Bethe log term"
"The predicted shift is divergent, but Bethe subtracted the term that corresponded to the linearly divergent vacuum energy shift for a free bare electron (= with illusory infinite bare mass and charge, this-p.4 ), essentially doing a mass renormalization to remove this higher-order divergence"
↑ Even after artificially removing infinities by illegitimate renormalization, QED cannot predict Lamb shift value, they have to artificially manipulate the left uncertain energy equation called Bethe log(arithm) ( this-p.3-left ).
(Fig.2) Quantum mechanics or QED can Not predict Lamb shift value expressed as unphysical Bethe logarithm, which must be artificially adjusted by inventing various fictional energy equations.
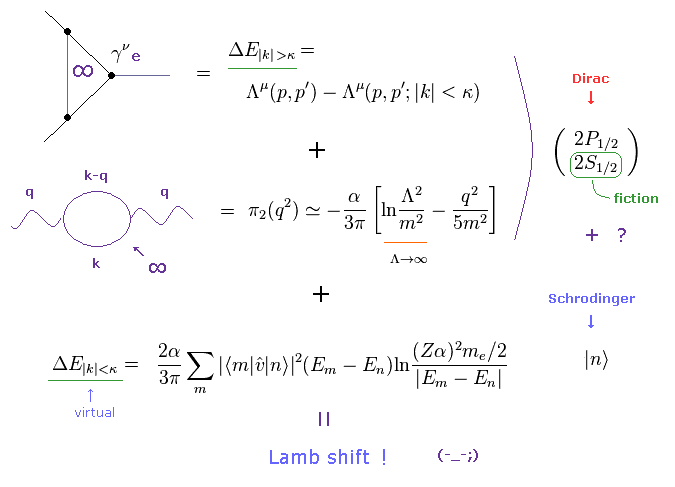
Even after QED artificially removes meaningless infinities by illegitimate renormalization, they just give uncertain unphysical energy equations called Bethe logarithm, which cannot predict (= just numerically or artificially gets ) Lamb shift value ( this-p.5-3rd~4th-paragraphs ).
This-p.3-left-4~6th-paragraphs say
"In this equation, K is a series that diverges to infinity.
Bethe decided to apply renormalization by substituting this
infinite value for the finite value of the electron's energy
(K = mc2
). There is No physical justification for making this
change."
"The average excitation energy (= called Bethe logarithm ) has been calculated numerically (= No analytical solution of Lamb shift ) "
"Bethe's fantastic calculation is based on data that was calculated later, so Bethe could Not have known it on his train journey. His calculation included this value that we suspect that was entered ad hoc to match the theoretical value with the experimental value. In the field of physics, this trick is known as a fudge factor."
↑ Bethe or quantum mechanics (= QED ) could Not calculate nor predict Lamb shift value even after artificially removing virtual infinities by illegitimate renormalization.
The remaining uncertain energy equation called Bethe logarithm ( this-p.4-(12) ) must be artificially (= or numerically ) adjusted or chosen to fit experimental Lamb shift.
This-p.2-(2) says
"is also known as the Bethe logarithm which has to be evaluated numerically (= Lamb shift was Not predicted analytically )"
This-last energy equation (= ΔE ) of Lamb shift still includes uncertain Lamb shift energy parameters of ω_{nj} (= | En - E0 | ) that must be artificially determined.
↑ There is No analytical solution of this Lamb shift or its free energy parameter = Bethe logarithm that must be artificially or numerically evaluated.
This-p.1-left says
"BL (= Bethe logarithm ) is one of the most complicated numerical evaluation quantities. Mainly because the logarithmic term
ln |En − E0| exists, where E0 and En are energies for the
initial and intermediate states"
"A variety of nonvariational methods and variational methods of calculating the hydrogen atom BL.. have been proposed (= artificially invented for obtaining Lamb shift ),... although giving a little poorer results"
this-p.9-right-last-paragraph says
"The Bethe logarithm ( this-p.3-left-5th-paragraph ) is a pure number
that has No known method of analytic calculation, so it
must be computed numerically for a given n an l"
Due to the useless QED unable to predict Lamb shift, later in 1956, Harriman proposed the artificial fictional energy equation expressing this uncertain Bethe logarithm's virtual average energy to match experimental Lamb shift ( this-p.1-abstract ).
↑ As shown in Fig.2-① , Harriman artificially changed the original uncertain Bethe logarithm (= ln k0/R ) into fictional energy equation consisting of many principal quantum numbers (= n ) and orbital angular momentums (= l ) of virtual excited energy ( this-p.1-(3)(5),p.2-(15) ).
This-p.1-(3) says
"Bethe's average excitation energy k0 may be (= 'may' means the artificially invented fictional equation, which is Not prediction of the original QED ) evaluated from the expression."
↑ This artificial creation of fictional energy equation shows the quantum mechanics or QED cannot predict Lamb shift.
In 1959, Schwartz and Tiemann ( this-p.35-(4.12) ) also artificially invented fictional hydrogen's (perturbation) energy Hamiltonian equation different from the original Schrodinger's hydrogen energy (= in Fig.2-②, the original Schrodinger's hydrogen energy = H0 of this-p.1-(1) is different from p.2-(5) and p.3-(10)'s fictional hydrogen's H1 energy equation of p.2-(2) ) to artificially explain Lamb shift values.
This-p.3-last says
"Brown et all suggested that one might evaluate (= the vague word "might" means this ad-hoc energy equation proposed by Schwartz is artificially invented, irrelevant to prediction of QED ) the Lamb shift by this differential equation approach."
So contrary to the overhyped (fake) news, QED based on unreal infinite virtual particles is unsuccessful, useless, unable to predict any physical values such as Lamb shift.
Also in Lamb shift in multi-electron atoms, they have to artificially adjust many free parameters and choose (fake) wavefunctions called basis sets that cannot predict any physical values such as Lamb shift ( this-p.6-(24) used artificial quasi-random parameters ).
This-p.1-left-2nd-3rd-paragraphs, p.1-right-2nd-paragraph say
"Bethe logarithm correction is
one quite remarkable term, which was firstly carried out
by Hans Bethe in 1947 to explain the splitting between
2S and 2P energy levels of hydrogen (= Lamb shift ).."
" Such a demand for calculation of Bethe logarithm in multi-electron systems is unrealistic"
"For multi-electron systems Bethe logarithm was the main obstacle in precision calculation"
As a result, QED is useless with No ability to predict any physical values such as the negligibly tiny Lamb shift that is irrelevant to QED (unreal) virtual particles nor 2s1/2.
↑ Actually physicists paradoxically insists the hydrogen atomic 1s ground-state also has Lamb shift energy splitting, through n = 1 energy level has only one 1s state with No 1p state, which means Lamb shift does Not need two ad-hoc energy levels of 2s1/2 and 2p1/2, but just needs only one 2p1/2 ( or 2s1/2 ) energy state.

Feel free to link to this site.