
Home page
QED is wrong.
Quantum field theory
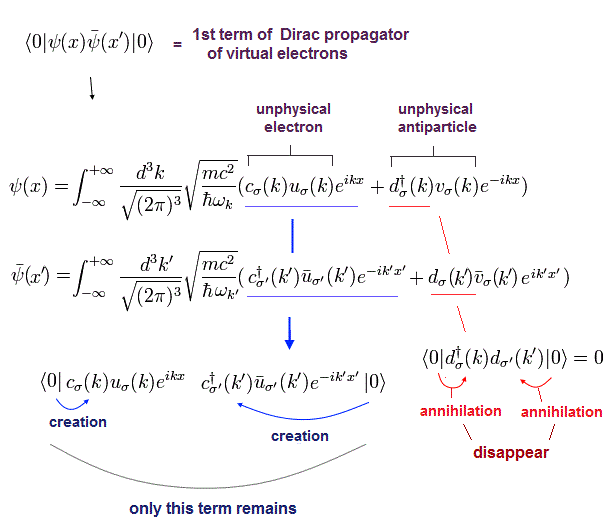
(Fig.1) Virtual electron (= fermion ) propagator used in QED is just an unphysical math irrelevant to the real phenomena or real particles.

All QED calculations use the unphysical equations called propagators allegedly representing virtual electrons (= fermions ) and photons violating Einstein relativity ( this-middle ) and diverging to meaningless infinities.
Fig.1 shows the fermion propagator consisting of two unphysical Dirac wavefunctions ( this-p.2, this-p.4 ) expressing (virtual) electrons and photons just as nonphysical math symbols (= c, c† d,.. ) with No real particle shape.
The p2 shows Einstein relativistic energy relation (= this page uses -1,+1,+1,+1 version of notation, and approximately, c = ℏ = 1 ) where p0 = E = -p0 is relativistic energy, pj = pj ( j = 1, 2, 3 ) is relativistic momentum ( this-p.11 ).
This fermion propagator containing virtual electrons is expressed as two Dirac spinors ψ(x)bar-ψ(x') when the time t > t' (= x0 > x'0 ) or -bar-ψ(x')ψ(x) when t' > t.
(Fig.2) Artificial change of fermion propagator utilizing unphysical infinities.
The unphysical fermion propagator Fig.1 can be changed into equations surrounded by the square of Fig.2 using Cauchy integration residue theorem and ±∞ infinities (of illusory virtual particles' energy ).
In the case of ① x0 > x'0 (= or t > t' ) of Fig.2, when p0 → -i∞, the exponential function e-ip0(x - x' ) becomes zero (and the upper integrated numbers become zero also in p0 → ±∞ ). which means the upper integration becomes equal to Cauchy clockwise integration (= real number integration from -∞ to +∞ and the integration from +∞ back to -∞ through imaginary number part of -i∞ ) around the solution of p0 = square root of p2j + m2 - iε (= ε is a very small positive number close to zero ).
In the case of ② x0 < x'0 (= or t < t' ) of Fig.2. when p0 → i∞, the exponential function becomes zero, which means the upper integration becomes equal to Cauchy counter-clockwise integration around p0 = -square root of p2j + m2 +iε where the momentums of pj ( j = 1, 2, 3 ) are also changed into -pj.
See this-p.8-p.14, this-p.2-5, this-p.3, this.
(Fig.3) Cauchy formula from -∞ to +∞ applied to unphysical electron propagator.
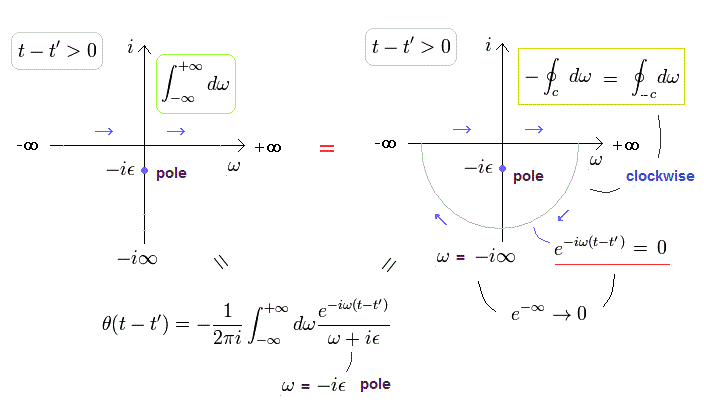
In Cauchy integral formula, when the integration surrounds some complex value (= in Fig.3, p0 = E-iε ε → +0 ), this (complex) value can be inserted into other function like f(p0) → f(E).
The sign of the counter-clockwise (or clockwise ) Cauchy integration is plus (or minus ).
In the upper Fig.3, the integral from -∞ to +∞ can be interpreted as the sum of integral of the real numbers of p0 from -∞ to +∞ and the integral of complex numbers of p0 from +∞ → -i∞ → -∞
↑ This equation is valid only when the integrated values become zero in p0 → ±∞ or p0 → -i∞ (= corresponding to the case of x0 - x'0 > 0 ← e-ip0( x0 - x'0 ) → 0 when p0 → -i∞ ).
See this-p.8-p.9, this-p.19-p.22
(Fig.4) Unphysical QED propagators lack real particle picture.
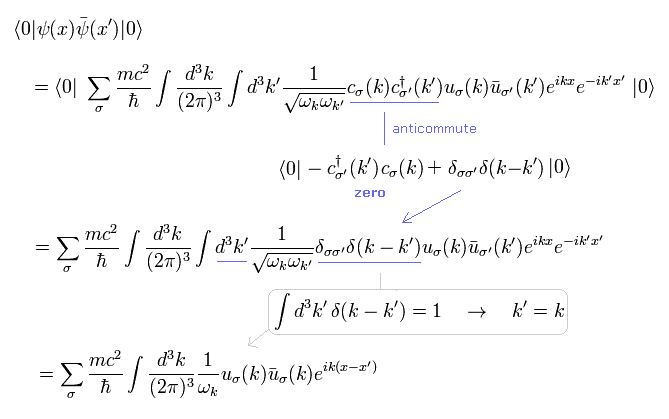
Using the unphysical Dirac electron-antiparticle wavefunctions, The first part (= ψ-bar-ψ ) of the fermion propagator of Fig.1 becomes like Fig.4
They use the artificial wrong 4 × 4 matrix expression consisting of u (= 4×1 matrix, this-p.10 )-bar-u (= 1×4 matrix called adjoint ), which cannot become the normal number.
(Fig.5) ↓ Unreal wrong matrix is used in QED propagator.
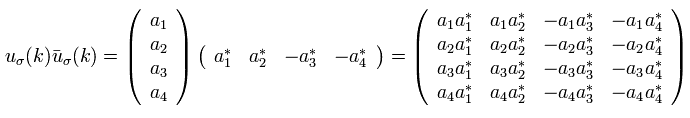
As shown in the upper Fig.5. QED fermion propagators rely on the unrealistic wrong 4×4 matrix (= called projection operator, this-p.26, this-p.24-lower ) consisting of u (= 4× matrix) and bar-u (= 1×4 matrix ), which is Not a normal matrix calculation nor becoming a normal number.
This artificial wrong matrix of 4×1 matrix + 1×4 matrix = 4×4 matrix is also one of QED illegitimate math tricks.
(Fig.6) Fermion propagators are wrong, based on inconsistent rules.

When inserting Dirac wavefunctions into the latter part of fermion propagator (= -bar-ψψ, this-p.13-(7.81), this-p.4-4.25 ), we originally obtain bar-v (= 1×4 matrix )-v (= 4×1 matrix) which is just the normal number ( this-p.24-(10.169), this-p.4-(7.22), this-p.10-(5.34) ), unlike u-bar-u case.
But QED illogically changes this original bar-v v (= number ) into v-bar-v (= wrong artificial 4×4 matrix, like u-bar-u ) to artificially obtain the fermion propagator for QED calculation ( this-p.12 ).
This illogical artificial change of Fig.6-lower is clearly wrong, inconsistent, invalidating all the QED calculations based on this electron (= fermion ) propagator.
This-p.27-(3.45) shows bar-ψ including bar-v, but its p.29-(3.63) illogically changes bar-ψ (= bar-v ) into ψ = v ( see also this-p.8-(5.27) and p.10-(5.34), this-p.168-p.169, this-p.1-lower ).
(Fig.7) Unphysical QED virtual photons.

In the same way as the unphysical fermion propagator, they obtain QED photon propagators ( this-p.8-p.9, this-p.18 this-p.5 ) which need the imaginary virtual photons with longitudinal polarization and negative probability.
As shown here, QED propagators of electrons (= fermion ) and photons rely on wrong inconsistent rules and unrealistic particles, which invalidates all the (artificial) QED calculations based on infinite virtual particles.

Feel free to link to this site.