Top page (correct Bohr model including the two-electron atoms).
Electron spin is an illusion !
Back to molecular bond ( CH4, H2O ) page.
First we explain about new Bohr model methane (CH4) computing methods in the program below.
This JAVA program will work in almost all browsers, I think.
Methane molecule (CH4) JAVA program.
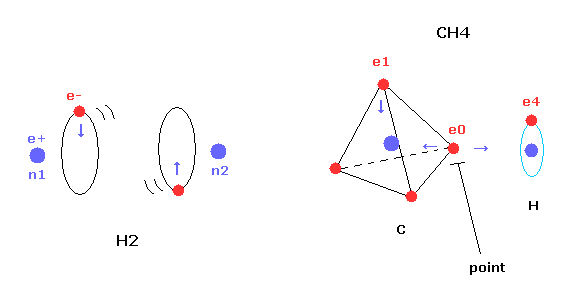
(Fig.1) Transverse projecting point of CH4.

In this page, we succeeded in expressing hydrogen molecule (H2) using Bohr's orbit correctly.
And we show the binding energy of H2 is maximum, when the internuclear distance is experimental value (= 7414 MM ).
Here we use new unit 1 MM = 1 × 10-14 meter.
But different from simple hydrogen molecule, carbon atom of methane (CH4) contains four tetrahedral distributed valence electrons.
So even if we try to arrange one electron of carbon parallel to the hydrogen's orbit, another of four electrons always protrudes toward hydrogen atom.
This projecting electron of carbon strongly attracts the hydrogen nucleus and lowers the potential energy.
And as I say later, this projecting electron is the key player to determine the instability.
(Fig.2) Structure of CH4 in computing program.
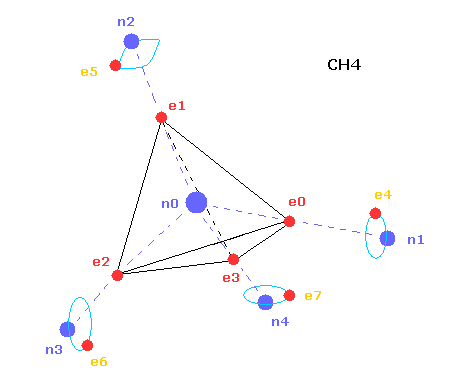
In the above computing program, we use the Fig.2 methane model.
Four valence electrons ( e0, e1, e2, e3 ) of carbon atom are arranged tetrahedrally.
And four hydrogen atomic nuclei also are distrubuted tetrahedrally.
As shown in Fig.2, electron e0 of carbon and n1 nucleus of hydrogen are on the same vector.
( In the same way, e1-n2, e2-n3, e3-n4 are on each same vector. )
(Fig.3) Cross section of CH4 (= x-z plane ).
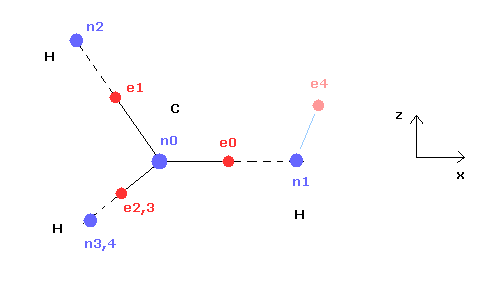
Fig.3 is the cross-sectional view ( x- z plane ) of Fig.2.
In the above program, we can change only the coordinate of electrons e0 and e4 in the textboxes.
( Only x coordinate of e0 and x, z coordinates of e4 can be changed. )
Based on the inputted coordinates of e0 and e4 in the textboxes, the remaining carbon electrons ( e1-e3 ) and hydrogen electrons ( e5-e7 ) are automatically arranged tetrahedrally.
So x coordinates of electrons 1, 2, 3 ( and H nuclei n2, 3, 4 ) are always the same.
( This program only shows each value, and not pictures due to the limit of screen, sorry. )
(Fig.4) Screen just after running program.
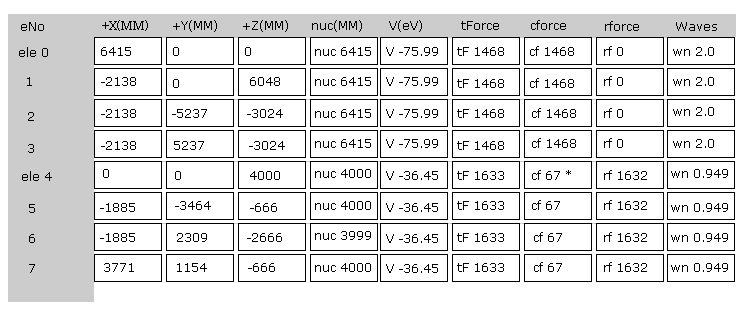
Fig.4 is the upper part, which appears on the screen just after you run the JAVA program.
ele 0, 1, 2, 3 are the electrons which belong to carbon atom.
+X(MM), +Y(MM), +Z(MM) are relative coordinates with respect to the nucleus, to which each electron belongs to.
( ele 0-3 belong to carbon nucleus n0, and ele4 - H nucleus n1, ele5-n2, ele6-n3, ele7-n4. )
"nuc" means the distance between each electron and nucleus, to which the electron belongs to.
Here new unit 1 MM = 1 × 10-14 meter is used.
"V(eV)" is potential energy of each electron.
"tForce" is total force, which acts on each electron.
"cforce" is the force component acting on each electron in the direction to center (= C nucleus ).
"rforce" is the force component acting on each electron ( e4-e7 ) toward each C nuc - H nuc line.
"Waves" is de Broglie waves contained in one orbit of each electron.
(Fig.5) Force = 1000.
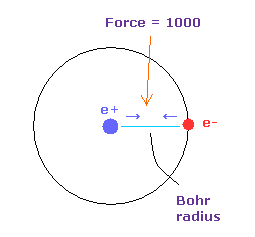
In Fig.4, the force between electron and nucleus in H atom ground state is supposed to be "1000".
So when the distance between electron and +e nucleus is Bohr radius, its force becomes 1000.
For example, the force of 1468 is 1.468 times that in H atom ground state.
We calculate each de Broglie wavelength from each kinetic energy (T).
Here Virial theorem ( -1/2V = T ) is used.
( "V" is potential energy. )
In cases of atoms (= single nucleus ) and H2 molecule, their calculations are simple.
But when a molecule contains two nuclei and asymmetric multi-electrons, we need to take care a little.
(Fig.6) O-H bond and the change of each potential energy
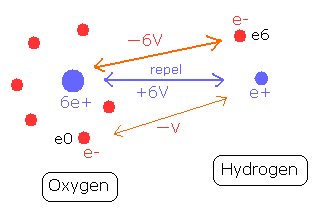
Fig.6 shows O-H bond of water molecule.
The hydrogen nucleus (e+) is attracted by the six electrons of the oxygen atom.
The potential energy between the hydrogen nucleus and one electron (e0) of oxygen is -V.
On the other hand, the oxygen nucleus is attracted only by one electron (e6) of hydrogen atom, so the potential energy between the oxygen nucleus and the hydrogen electron (e6) is - 6V, which bond strength is six times stronger than the above case.
(Fig.7) Attracrive V is canceled by repulsive V.
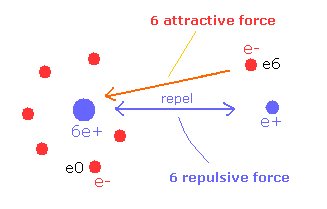
So e6 does much work to bind two repulsive positive nuclei, which makes the e6 potential energy higher than this.
( This means negative potential energy -6V is almost canceled out by positive +6V between nuclei. )
Considering this fact, in the programs, after calculating potential energies between electron-electoron and electron-nucleus, the potential energies among positive nuclei are distributed to each electron.
For example, when this repulsive potential energy is +6V, the distribution ratio is 6:1 in e6 and e0. (= -6V: -V )
As the oxygen has six e0-e5 electrons, +6V × 6/(1x6 +6) = +6V / 2 = +3V is distributed to e6, and +6V × 1/(1x6+6)= +6V / 12= +3V / 6 is distributed to e0.
( So almost same +3V repulsive potential is distributed to each side of O-H bond. )
In the programs above, we calculate each electron's V ( = rhp[el][6] ) with other nuclei, and in proportion to the magnitude of rhp[el][6], total repulsive potential energy (= pota ) between nuclei are distributed to each electron.
From each kinetic energy, we can get the electron's velocity (= v ) and de Broglie wavelength (= h/mv ).
(Eq.1) Total force F = centrifugal force.
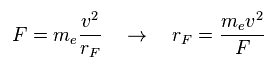
In the program, we compute x, y, z componetns of forces acting on each electron.
( rhp[el][0, 1, 2] = x, y, z component force. )
Here we suppose total forces F of them are some centrifugal forces.
From the relation of Eq.1, we can get ( approximate ) rotation radius (= rF ).
(Eq.2) de Broglie wave in one orbit.
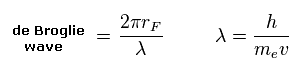
Using the de Broglie relation ( λ = h/mv ), we caluclate the number of de Broglie waves included in one orbit (= 2πrF ).
Carbon outer electrons e0-e3 should be "2", and hydrogen's electrons e4-e7 should be "1" in de Broglie waves.
(Fig.8) Carbon "effective" charge = +Ze.
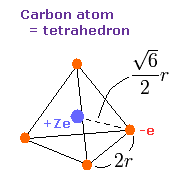
As shown in this page, the radius of carbon inner 1s electrons is almost 930 MM (= 0.0930 × 10-10 meter ).
Considering two inner 1s electrons are a little apart from carbon nucleus +6e, it is natural that we think the central positive charge Z of four outer electrons is a little bigger than +4e (= +6e -2e ).
The side length of the tetrahedron is supposed to be 2r, as shown in Fig.8.
( Four vertices of Fig.8 represent four outer electrons of carbon. )
The total ionization energy (E) of the four valence electrons is -148.024 eV, so we suppose potential energy (V) becomes 2 × -148.024 = -296.048 eV due to Virial theorem.
Calculating the potential energy (V) using Fig.8 model, this V ( eV --> J ) becomes,
(by calculating the interactions between each electron - nucleus and electron-electron,)
Sample JAVA program to compute de Broglie wave of carbon.
In this program, after inputting central positive charge Z ( almost 4.0 ), it computes potential energy V, force, and de Broglie wave in one orbit using Virial theorem ( T = -E = - 1/2V ) and Eq.3 - Eq.7.
On the screen, the rorating radius ( MM ) and de Broglie waves in one orbit are shown.
(Eq.3) Total potential V of Fig.8.
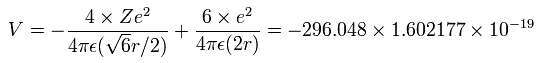
And the total kinetic energy (T) of the four electrons is 148.024 (eV) due to Virial theorem,
(Eq.4)
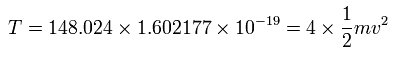
And by calculating the Coulomb forces among the particles of Fig.8, total force (F) acting on an electron (toward nucleus) becomes,
(Eq.5)
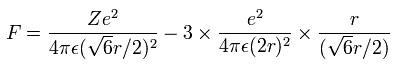
Using the above velocity (v) (of T) and F, we suppose the centrifugal force is equal to the force (F), as follows,
(Eq.6)
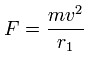
This r1 is "temporary" radius, which appears by this relation.
Using this r1, we can calculate the number of de Broglie's waves (wn) contained in one orbit, as follows,
(Eq.7)
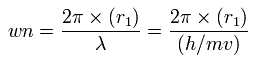
When Z = +4.0, this wn becomes 1.87 (almost 1.9) and rotating radius is almost 6000 MM.
And when Z = +4.22, this wn becomes just 2.00 and rorating radius is almost 6400 MM.
Sample JAVA program -- Visualization of carbon four valence electrons. ( central charge +4.22. )
Actually, if you run the program above, and choose "1.0" or "2.0" de Broglie wave in the scrollbar, and click "orbit" button, you can understand when Z = 4.22, one orbit is just 2.0 de Broglie wavelength, and its rotating radius (= nuc ) is about 6400 MM (= 0.6400 × 10-10 meter. )
See also this page.
Here we use this approximate value of 4.22 as central positive charge of carbon (= "den" in the program, and aim at de Broglie wave of 2.0.
(Fig.9) de Broglie waves of C-H bond
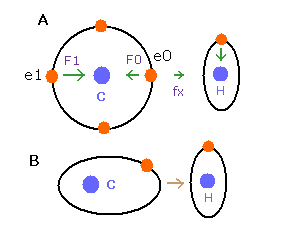
In the e0 electron Fig.9A, we cannot use the upper calculating method of de Broglie's waves as it is.
In the electron 0 (e0) of carbon (C), due to the opposite attractive force (fx) from the hydrogen nucleus, force F0 becomes weaker than force F1 of electron 1, as shown in Fig.9A.
So, in Eq.1, "temporary" radius r1 of e0 becomes longer than e1.
This means more de Broglie's waves (> 2.0) are contained in e0 orbit than e1 ( < 2.0 ), when we use the above calculating methods directly.
But if we pay attention to only one electron's orbit (Fig. 9B), the number of de Broglie's waves ( = 2.0 ) is kept by changing the position and shape of its orbit.
(A positive H nucleus translates this electron's orbit a little, and make it "elliptical".)
So when we calculate C-H carbon electron's wave in one orbit, we condsider the forces and energies only inside carbon atom, approximately.
( In the program, teqq[el][3] means each potential V only in carbon atom. )
(Fig.10) Each force in C-H bond
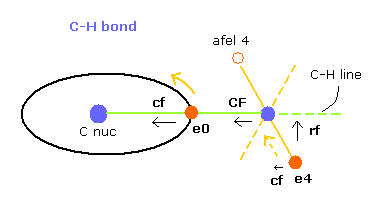
In this program, "cf" means the force component acting on each electron toward C nucleus.
And "rf" means force acting on electron 4-7 toward ( perpendicular to ) each C-H line.
"afel 4" means the electron's position after moving it in the direction of force.
( So each electron is oscillating transversely around this place. )
For the electron's orbit to be stable at some point, this "cf" of e4 is positive, and "cf" of afel 4 is negative.
And their absolute values need to be almost the same to be stable.
( This is one of important points in stable molecular bonds. )
"CF" means force acting on each H nucleus toward C nucleus.
So when these CF and cf are positive values, these particles are attracted toward central C nucleus.
(Fig.11) "afel 4" position.
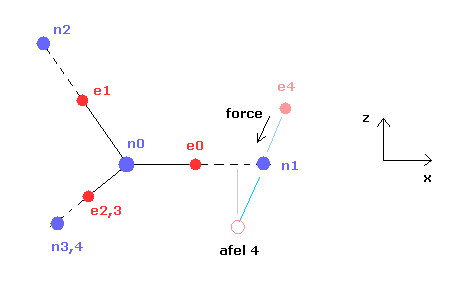
When calculating "afel 4" x coordinate, we use the force component ratio of "cf" to "rf".
In the program, "cf" componment of force is expressed as rhp[el][4], and "rf" component is rhp[el][5].
And z (and y ) coordinate of afel 4 is supposed to be equal to the original e4.
(Fig.12) Average positions ?

When we try to calculate de Broglie waves and forces of each particle using Fig.12 distribution, four outer electrons and hydrogen nuclei are attracted to each other more than the average values.
( These standard coodinates are expressed using variables hpr[el][0-2] in the program. )
Carbon outer electron's orbit radius is about 6400 MM, which is almost same as Bohr radius 5292 MM of hydrogen atom.
But carbon outer electron's orbit is two de Broglie wavelength, which means their velocity is almost twice faster than that of H atom electron.
So we need to consider average distribution about carbon atom, when we consider the interaction with H atom.
(Fig.13) Average positions of outer electrons of carbon.
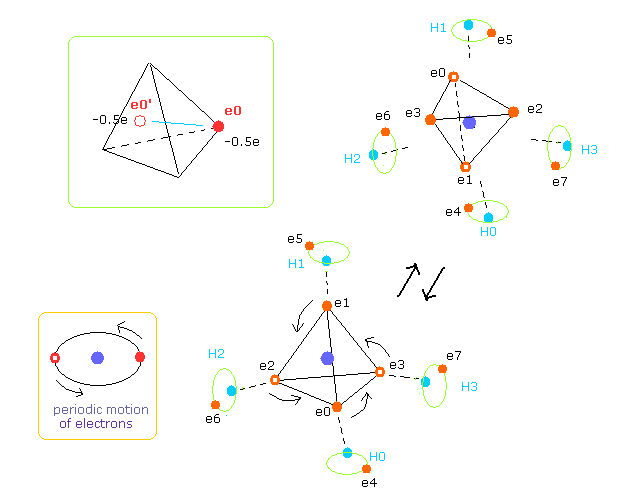
As shown in Fig.13, four outer electrons of carbon are moving on almost elliptical orbits.
So the opposite positions of each electron is important to take average values, too.
Actually Virial theorem is valid, when their motions are equal to average ones during infinite time period.
In the program, we get the electrons e0-e3's opposite positions with respect to carbon nucleus.
( Coordinate variables are hpr3[el][0,1,2] = hpr3[el][x,y,z] = -hpr[el][x,y,z]. )
So carbon's four outer electrons moving faster can be considered as eight electrons with half charge ( -1.0e → -0.5e, -0.5e × 8 = -4e ).
( Of course, when we compute repulsive potentials among electrons 0-3 themselves, the original four valence electrons need to be used. )
"4-averwave" ( or "0-averwave" ) are average de Broglie waves of electron 4 ( or 0 ) considering original ele4 and afel-4.
We try to get each coordinate, when these average de Broglie waves becomes 1.0 in ele 4 ( or 2.0 in ele 0 ).
When you choose the C-H bond length and click "C-H button" next to it, C-H length of methane is changed.
( The experimental value of C-H bond length is 10900 MM. )
"aCF", and "tV after" means the force acting on H nucleus, and total V, when electron 4-7 positions are afel 4-7.
In this section, we explain about the program below,
( About the basic computing methods, see the above section. )
The difference is H2O is more asymetric than CH4.
So oxygen electrons 0-5 cannot keep octahedral structure.
(Fig.14) Change of "octahedral" structure in O-H bond
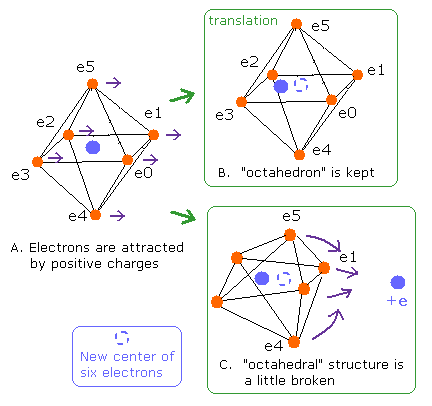
We get the central coordinate of oxygen electrons 0-5 as noxx[0-2] in the program.
We suppose oxygen central charge ( den = + 6.273, which is explained later ) is at this central position.
And only inside oxygen atom, we obtain force, potential energy and de Broglie waves about ele0-5.
And "O nuc FX, FY, FZ" means force component acting on O nucleus.
"On" and "Hn" of H0 (or H1 ) nucleus mean force components acting on H0 (or H1 ) nucleus.
( "On" is toward O nucleus, "Hn" is toward another H nucleus. )
"0-averwave" means the average de Broglie wave in one orbit of electron 0-5.
"6-averwave" means the average de Broglie of electron 6 and electron 6 after moving following force ( See also Fig.10 ).
Water molecule (H2O) JAVA program.
(Fig.15) Oxygen valence electrons.
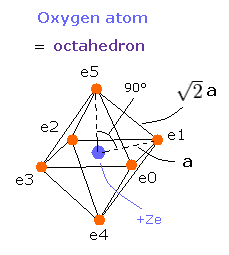
In Fig.15, the distance between an electron and the central positive charge is a.
According to the Virial theorem, "average" total potential (V) and kinetic (T) energies satisfy the relation,
< V > = -2 × < T > , E = V + T
The total ( ionization ) energy (E) of the six valence electrons is -433.103 eV, so this potential energy (V) becomes 2 × -433.103 = -866.206 eV.
When we calculate this potential energy (V) using Fig.15 model, this V ( eV --> J ) becomes,
(by calculating the interactions between each electron - nucleus and electron-electron,)
(Eq.8)
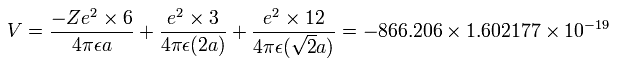
And the total kinetic energy (T) of the six electrons is 433.103 (eV) according to Virial theorem,
(Eq.9)
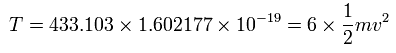
And by calculating the Coulomb forces among the particles of Fig.15, the force (F) acting on electron 0 (toward nucleus) becomes,
(Eq.10)
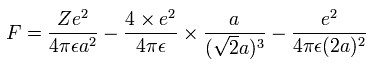
Using the above velocity (v) (of T) and F, we suppose the centrifugal force is equal to the force (F), as follows,
(Eq.11)
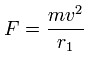
This r1 is "temporary" radius, which appears by this relation.
Using this r1, we can calculate the number of de Broglie's waves (wn) contained in one orbit, as follows,
(Eq.12)
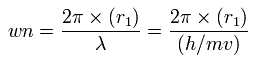
When Z = 6.0, this wn becomes 1.88 (almost 1.9).
And when Z = 6.273, this wn becomes just 2.00.
In this case, rorating radius of 2s electron is about 4596 MM.
( Here new unit 1 MM = 10-14 meter is used. )
As shown in the O6+ and O5+ ion sections, the distance between two 1S electrons and nucleus is about 700 MM.
So this result (in which the average distance is about 4596 MM ) means that six valence electrons don't collide with the inner 1S electrons, and can move safely.
And due to this distance of 700 MM, the effective positive charge becomes a little bigger than +6e (= +8e - 2e ).
For example, the O-H bond length of water (H2O) is 9584 MM, so this computing value of oxygen radius using Bohr's orbit (= 4596 MM ) is good.

2013/3/6 updated. Feel free to link to this site.