《Franken／Mutant》
《Ｆｉｓｈ 基本形》 は ある数字が ２つ以上の行（列）［ｂａｓｅ ｓｅｔ］で配置可能なマスが その行（列）と同じ数の列（行）［ｃｏｖｅｒ ｓｅｔ］に限定されると その数字が配置できないマスが見つかるものでした。 それらの 行（列）は”大マス”を含んだ領域であっても，その数字が配置できないマスが見つかることがあります。 行・列に 大マスを含む場合を ”Franken”， 行・列・大マス が複雑に組み合わさったものを ”Mutant”と呼びます。 このページでは 領域の数が ３つであるものについて説明します。
３つの 行・列 が関係した 《Ｆｉｓｈ 基本形》は 三人の賢い見張兵排除（Swordfish）です。
練習問題へ
《Ｆｉｓｈ 基本形》の テクニック”三人の賢い見張兵排除(Swordfish)”では base sets，cover sets は ３つの行・列 でした。 各々の sets は，行，列 だけでなく，大マスも含めた 任意の領域 であっても 同様の排除が成立することがあります。 base sets・cover sets が任意の３領域であるものを ”乱戦賢い三見張兵排除” と名付けて説明します。
［テクニック”乱戦賢い三見張兵排除”の例 １］
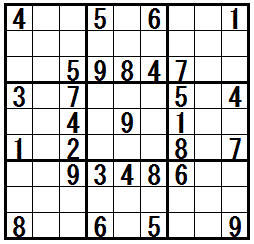
base sets に 大マス が含まれる例題です。利用する排除のテクニックは Franken Swordfish と呼ばれます。
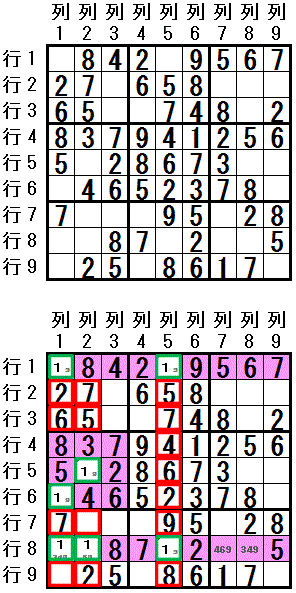数字１ が，配置可能なマスは
行１ では，行１列１，行１列５
行８ では，行８列１，行８列２，行８列５
大マス４ では，行５列２，行６列１
です（base sets:行１，行８，大マス４）。
これら ７つのマス は，３つの領域 列１，列２，列５(cover sets) に含まれます（カバーされています）。
もし，これら３つの領域（列１，列２，列５）のマスで base sets に含まれないマス（例えば 列２ の 行７列２）に 数字１ が配置されると， その領域（列２）で base sets に含まれるマス（行５列２，行８列２）には 数字１ は配置できません。 すると， cover sets の残りの領域（列１，列５）２つだけの中に，base sets である３つの領域（行１，行８，大マス４）で 数字１ を配置する ３つのマス（行１列１または行１列５ と 行６列１ と 行８列１または行８列５） を確保しなければならなくなり 矛盾を生じます。
よって，cover sets（列１，列２，列５）では，base sets に 含まれないマス には 数字１ を配置できないことがわかります。
ダウンロードいただいたソフトでは，
▼乱戦賢い三見張兵排除 排除数字▼ 1 行 7 列 2
排除数字は
行 1, 行 8, 大マス 4 (base sets)で配置可能なマスに同一のものがなく，
それらすべてが 列 1, 列 2, 列 5 (cover sets)でカバーされているので
cover sets では base sets に含まれないマスには配置できない
と，表示されます(新たに得られた排除情報以外は表示しません)。
テクニック”お山の大将”により，行７列２ の 数字６ が確定します。
複数の base set の領域に同じマスが含まれていても構いませんが，当該数字が配置可能なマスは 必ず １つの base set にだけ 含まれます（複数の base set には含まれません）。
ダウンロードいただいたソフトでは 数字が配置可能なマスが３つか２つに限られる 行，列，大マス の配置可能なマスを黄色く塗りつぶした ペンシルマーク を表示可能です。 数字１ の例は ここ をクリックしてください。
（発展と補足で後述するように，乱戦賢い三見張兵排除では 当該の数字が base set の領域で 配置可能なマスの数が３つまでではなく，４つ以上 でも排除が成立する可能性があります）
ペンシルマークを利用しても，乱戦賢い三見張兵排除 が適応できるかどうかを確認することは 根気のいる作業になります。
［テクニック”乱戦賢い三見張兵排除”の例 ２］
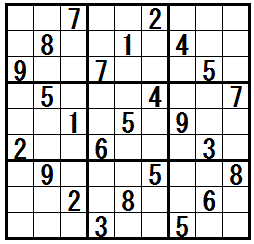
次の例題に対して 行・列･大マス を複雑に検討して 排除する数字を決定してみます。ここで解説する排除のテクニックは Mutant Swordfish と呼ばれます。
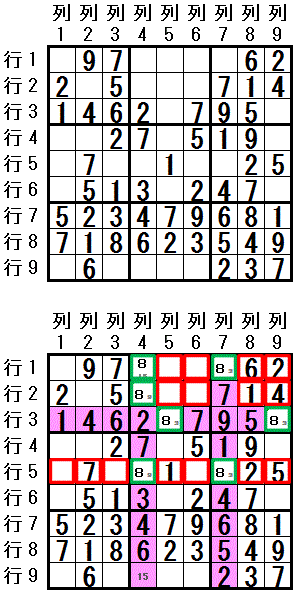数字８ が，配置可能なマスは
行３ では，行３列５，行３列９
列４ では，行１列４，行２列４，行５列４ ＊）
列７ では，行１列７，行５列７
です（base sets:行３，列４，列７）。
これら ７つのマス は，３つの領域 行５，大マス２，大マス３(cover sets) に含まれます（カバーされています）。
もし，これら３つの領域（行５，大マス２，大マス３）のマスで base sets に含まれないマス（例えば 大マス２ の 行１列５）に 数字８ が配置されると， その領域（大マス２）で base sets に含まれるマス（行３列５，行１列４，行２列４）には 数字８ は配置できません。 すると， cover sets の残りの領域（行５，大マス３）２つだけの中に，base sets である３つの領域（行３，列４，列７）で 数字８ を配置する ３つのマス（行３列９ と 行５列４ と 行１列７または行５列７） を確保しなければならなくなり 矛盾を生じます。
よって，cover sets（行５，大マス２，大マス３）では，base sets に 含まれないマス には 数字８ を配置できないことがわかります。
ダウンロードいただいたソフトでは，
▼乱戦賢い三見張兵排除 排除数字▼ 8 行 2 列 5
▼乱戦賢い三見張兵排除 排除数字▼ 8 行 2 列 6
▼乱戦賢い三見張兵排除 排除数字▼ 8 行 5 列 1
▼乱戦賢い三見張兵排除 排除数字▼ 8 行 5 列 6
排除数字は
行 3, 列 4, 列 7 (base sets)で配置可能なマスに同一のものがなく，
それらすべてが 行 5, 大マス 2, 大マス 3 (cover sets)でカバーされているので
cover sets では base sets に含まれないマスには配置できない
と，表示されます(新たに得られた排除情報以外は表示しません)。
テクニック”お山の大将”により，行２列６ の 数字６ が確定します。
＊） 数字８ が 行９列４ に配置できないことは， 列４ では，行２列４ と 行５列４ の２つのマスには，数字８，９ の２つしか配置できないことからわかります（二都物語排除）
この例題は base sets を 列４，列７，大マス１ cover sets を 行１，行２，行５ とした Franken Swordfish によって 数字８ が 行２列５，行９列５ に配置できないことを発見しても解き進めることができます （ここ をクリックしてください）。 cover sets に 大マス を含めた Franken Swordfish（base sets：行３，行４，行６ cover sets：列５，列９，大マス４）と考えても，同様に排除される数字が見つかります。確認してみてください。
［名称”乱戦賢い三見張兵排除”の由来］
”賢い見張兵排除”では，守備線，連絡路は，縦横（行と列）整然としていました。まだ戦闘は起こっていません。 いざ戦闘が始まって乱戦状態になると，拠点から監視している場所は縦横入り乱れ（行列の混在），拠点の直近の場所（大マス）しか守備できないかも知れません。 拠点間の連絡路も縦横入り乱れ，直近の場所にしか連絡が取れなくなることもあります。 それでも兵を拠点に賢く配置した守備体系を採れば，拠点以外の連絡可能な場所は兵を配置しなくても管理下におけます。
［テクニック”乱戦賢い三見張兵排除”の発展 と 補足］
発展１）関連する領域の数 関連する領域の数を ３つ から ４つ（乱戦賢い四見張兵排除：Franken Jellyfish, Mutant Jellyfish），５つ（乱戦賢い五見張兵排除：Franken Squirmbag, Mutant Squirmbag），・・・ と増やしても排除が成立する可能性があります。
発展２）base sets で 当該の数字が配置可能なマスの数
大マスが関連する場合，当該の数字が配置可能なマスの数が３つまでではなく，４つ以上 でも排除が成立する可能性があります。
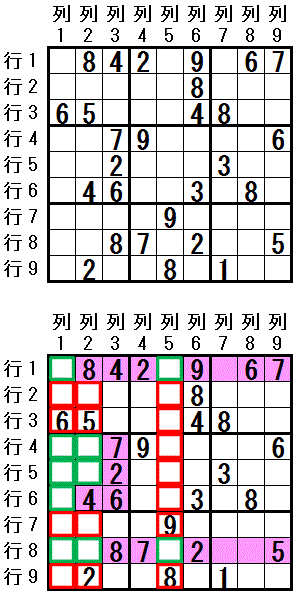［テクニック”乱戦賢い三見張兵排除”の例 １］の図から配置されている数字の一部を削除しています。
例１ と同様に，base sets は 行１，行８，大マス４，cover sets は 列１，列２，列５ です。
大マス４では 数字１ が配置可能なマスの数が ５つ あります。 それでも base sets（行１，行８，大マス４） で 数字１ が配置可能なマスは，列１，列２，列５(cover sets) にカバーされています。 この場合でも，Franken Swordfish（乱戦賢い三見張兵排除）が成立して，数字１を 行７列２ に配置できないことがわかります （その他 行２列１，行２列２，行２列５，行３列５，行４列５，行５列５，行６列５ にも 数字１ を配置できないことがわかります）。
この図から初級のテクニックだけを使って手を進めると，数字３ に関して base sets を 列１，列５，大マス９，cover sets を 行１，行８，行９ とした”乱戦賢い三見張兵排除”が適応できる局面が現れます。問題図 をクリックしてください。
発展３）Finned/Sashimi Franken/Mutant Fish
見張塔過多排除（Finned/Sashimi） と同じく base set で配置可能なマスが cover set に完全にカバーされずに余分にあっても， 数字の配置が排除されるマスが見つかることがあります。
二市街戦狙いうち排除（Finned Franken/Mutant X-Wing），三市街戦狙いうち排除（Finned Franken/Mutant Swordfish），四市街戦狙いうち排除（Finned Franken/Mutant Jellyfish）と名付けています。 市街戦（乱戦）になっても，余分なマスから排除されるマスを狙いうちできることを意識しています。
ダウンロードいただいたソフトでは，発展１）で領域の数が ５以上 のものはプログラムしていません。
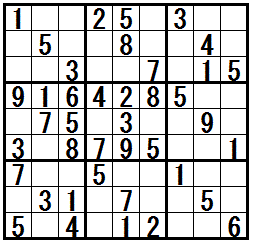
［練習問題 ”乱戦賢い三見張兵排除”］
解答の途中で テクニック”乱戦賢い三見張兵排除” が必要になる問題です。
一番左の問題は 問題局面に直接 テクニック”乱戦賢い三見張兵排除” が適応されます。
一番右の問題は テクニック”乱戦賢い三見張兵排除”を２回利用します。
問題図をクリックすると，正解と解答過程の一例が表示されます。
《Ｆｉｓｈ 基本形》 は ある数字が ２つ以上の行（列）［ｂａｓｅ ｓｅｔ］で配置可能なマスが その行（列）と同じ数の列（行）［ｃｏｖｅｒ ｓｅｔ］に限定されると その数字が配置できないマスが見つかるものでした。 それらの 行（列）は”大マス”を含んだ領域であっても，その数字が配置できないマスが見つかることがあります。 行・列に 大マスを含む場合を ”Franken”， 行・列・大マス が複雑に組み合わさったものを ”Mutant”と呼びます。 このページでは 領域の数が ３つであるものについて説明します。
３つの 行・列 が関係した 《Ｆｉｓｈ 基本形》は 三人の賢い見張兵排除（Swordfish）です。
練習問題へ
《Ｆｉｓｈ 基本形》の テクニック”三人の賢い見張兵排除(Swordfish)”では base sets，cover sets は ３つの行・列 でした。 各々の sets は，行，列 だけでなく，大マスも含めた 任意の領域 であっても 同様の排除が成立することがあります。 base sets・cover sets が任意の３領域であるものを ”乱戦賢い三見張兵排除” と名付けて説明します。
［テクニック”乱戦賢い三見張兵排除”の例 １］
base sets に 大マス が含まれる例題です。利用する排除のテクニックは Franken Swordfish と呼ばれます。
数字１ が，配置可能なマスは行１ では，行１列１，行１列５
行８ では，行８列１，行８列２，行８列５
大マス４ では，行５列２，行６列１
です（base sets:行１，行８，大マス４）。
これら ７つのマス は，３つの領域 列１，列２，列５(cover sets) に含まれます（カバーされています）。
もし，これら３つの領域（列１，列２，列５）のマスで base sets に含まれないマス（例えば 列２ の 行７列２）に 数字１ が配置されると， その領域（列２）で base sets に含まれるマス（行５列２，行８列２）には 数字１ は配置できません。 すると， cover sets の残りの領域（列１，列５）２つだけの中に，base sets である３つの領域（行１，行８，大マス４）で 数字１ を配置する ３つのマス（行１列１または行１列５ と 行６列１ と 行８列１または行８列５） を確保しなければならなくなり 矛盾を生じます。
よって，cover sets（列１，列２，列５）では，base sets に 含まれないマス には 数字１ を配置できないことがわかります。
ダウンロードいただいたソフトでは，
▼乱戦賢い三見張兵排除 排除数字▼ 1 行 7 列 2
排除数字は
行 1, 行 8, 大マス 4 (base sets)で配置可能なマスに同一のものがなく，
それらすべてが 列 1, 列 2, 列 5 (cover sets)でカバーされているので
cover sets では base sets に含まれないマスには配置できない
と，表示されます(新たに得られた排除情報以外は表示しません)。
テクニック”お山の大将”により，行７列２ の 数字６ が確定します。
複数の base set の領域に同じマスが含まれていても構いませんが，当該数字が配置可能なマスは 必ず １つの base set にだけ 含まれます（複数の base set には含まれません）。
ダウンロードいただいたソフトでは 数字が配置可能なマスが３つか２つに限られる 行，列，大マス の配置可能なマスを黄色く塗りつぶした ペンシルマーク を表示可能です。 数字１ の例は ここ をクリックしてください。
（発展と補足で後述するように，乱戦賢い三見張兵排除では 当該の数字が base set の領域で 配置可能なマスの数が３つまでではなく，４つ以上 でも排除が成立する可能性があります）
ペンシルマークを利用しても，乱戦賢い三見張兵排除 が適応できるかどうかを確認することは 根気のいる作業になります。
［テクニック”乱戦賢い三見張兵排除”の例 ２］
次の例題に対して 行・列･大マス を複雑に検討して 排除する数字を決定してみます。ここで解説する排除のテクニックは Mutant Swordfish と呼ばれます。
数字８ が，配置可能なマスは行３ では，行３列５，行３列９
列４ では，行１列４，行２列４，行５列４ ＊）
列７ では，行１列７，行５列７
です（base sets:行３，列４，列７）。
これら ７つのマス は，３つの領域 行５，大マス２，大マス３(cover sets) に含まれます（カバーされています）。
もし，これら３つの領域（行５，大マス２，大マス３）のマスで base sets に含まれないマス（例えば 大マス２ の 行１列５）に 数字８ が配置されると， その領域（大マス２）で base sets に含まれるマス（行３列５，行１列４，行２列４）には 数字８ は配置できません。 すると， cover sets の残りの領域（行５，大マス３）２つだけの中に，base sets である３つの領域（行３，列４，列７）で 数字８ を配置する ３つのマス（行３列９ と 行５列４ と 行１列７または行５列７） を確保しなければならなくなり 矛盾を生じます。
よって，cover sets（行５，大マス２，大マス３）では，base sets に 含まれないマス には 数字８ を配置できないことがわかります。
ダウンロードいただいたソフトでは，
▼乱戦賢い三見張兵排除 排除数字▼ 8 行 2 列 5
▼乱戦賢い三見張兵排除 排除数字▼ 8 行 2 列 6
▼乱戦賢い三見張兵排除 排除数字▼ 8 行 5 列 1
▼乱戦賢い三見張兵排除 排除数字▼ 8 行 5 列 6
排除数字は
行 3, 列 4, 列 7 (base sets)で配置可能なマスに同一のものがなく，
それらすべてが 行 5, 大マス 2, 大マス 3 (cover sets)でカバーされているので
cover sets では base sets に含まれないマスには配置できない
と，表示されます(新たに得られた排除情報以外は表示しません)。
テクニック”お山の大将”により，行２列６ の 数字６ が確定します。
＊） 数字８ が 行９列４ に配置できないことは， 列４ では，行２列４ と 行５列４ の２つのマスには，数字８，９ の２つしか配置できないことからわかります（二都物語排除）
この例題は base sets を 列４，列７，大マス１ cover sets を 行１，行２，行５ とした Franken Swordfish によって 数字８ が 行２列５，行９列５ に配置できないことを発見しても解き進めることができます （ここ をクリックしてください）。 cover sets に 大マス を含めた Franken Swordfish（base sets：行３，行４，行６ cover sets：列５，列９，大マス４）と考えても，同様に排除される数字が見つかります。確認してみてください。
［名称”乱戦賢い三見張兵排除”の由来］
”賢い見張兵排除”では，守備線，連絡路は，縦横（行と列）整然としていました。まだ戦闘は起こっていません。 いざ戦闘が始まって乱戦状態になると，拠点から監視している場所は縦横入り乱れ（行列の混在），拠点の直近の場所（大マス）しか守備できないかも知れません。 拠点間の連絡路も縦横入り乱れ，直近の場所にしか連絡が取れなくなることもあります。 それでも兵を拠点に賢く配置した守備体系を採れば，拠点以外の連絡可能な場所は兵を配置しなくても管理下におけます。
［テクニック”乱戦賢い三見張兵排除”の発展 と 補足］
発展１）関連する領域の数 関連する領域の数を ３つ から ４つ（乱戦賢い四見張兵排除：Franken Jellyfish, Mutant Jellyfish），５つ（乱戦賢い五見張兵排除：Franken Squirmbag, Mutant Squirmbag），・・・ と増やしても排除が成立する可能性があります。
発展２）base sets で 当該の数字が配置可能なマスの数
大マスが関連する場合，当該の数字が配置可能なマスの数が３つまでではなく，４つ以上 でも排除が成立する可能性があります。
［テクニック”乱戦賢い三見張兵排除”の例 １］の図から配置されている数字の一部を削除しています。例１ と同様に，base sets は 行１，行８，大マス４，cover sets は 列１，列２，列５ です。
大マス４では 数字１ が配置可能なマスの数が ５つ あります。 それでも base sets（行１，行８，大マス４） で 数字１ が配置可能なマスは，列１，列２，列５(cover sets) にカバーされています。 この場合でも，Franken Swordfish（乱戦賢い三見張兵排除）が成立して，数字１を 行７列２ に配置できないことがわかります （その他 行２列１，行２列２，行２列５，行３列５，行４列５，行５列５，行６列５ にも 数字１ を配置できないことがわかります）。
この図から初級のテクニックだけを使って手を進めると，数字３ に関して base sets を 列１，列５，大マス９，cover sets を 行１，行８，行９ とした”乱戦賢い三見張兵排除”が適応できる局面が現れます。問題図 をクリックしてください。
発展３）Finned/Sashimi Franken/Mutant Fish
見張塔過多排除（Finned/Sashimi） と同じく base set で配置可能なマスが cover set に完全にカバーされずに余分にあっても， 数字の配置が排除されるマスが見つかることがあります。
二市街戦狙いうち排除（Finned Franken/Mutant X-Wing），三市街戦狙いうち排除（Finned Franken/Mutant Swordfish），四市街戦狙いうち排除（Finned Franken/Mutant Jellyfish）と名付けています。 市街戦（乱戦）になっても，余分なマスから排除されるマスを狙いうちできることを意識しています。
ダウンロードいただいたソフトでは，発展１）で領域の数が ５以上 のものはプログラムしていません。
［練習問題 ”乱戦賢い三見張兵排除”］
解答の途中で テクニック”乱戦賢い三見張兵排除” が必要になる問題です。
一番左の問題は 問題局面に直接 テクニック”乱戦賢い三見張兵排除” が適応されます。
一番右の問題は テクニック”乱戦賢い三見張兵排除”を２回利用します。
問題図をクリックすると，正解と解答過程の一例が表示されます。