
トップページ (ヘリウムも含む正確な新ボーア模型)
光子のベルの不等式の破れは幻想。
D-Wave の 量子コンピューターは本当か ?
量子 "チェシャ猫" のトリック。 (14/8/31)
(Fig.1) ”量子コンピューター”は 本当に実用化できるのか?

量子コンピューターは 通常のコンピューターよりも 格段に 速い夢のマシーンと言われている。
色んなジャーナル、ニュースメディアなどが、今までに幾度となく 一般人に 量子コンピューターの華やかな側面をアピールしてきた。
しかし、現実の話、量子コンピューターにおける研究は すでに 完全に行き詰っていると言える。
それにも関わらず、その道の物理学者達や専門誌は 量子コンピューターは 近い未来に実現可能だと さかんに 誇大宣伝している状況である。
このページでは、これら "まやかし" の文句と裏腹に、量子コンピューターが
まったく 実現不可能な 単なる ”絵に描いた餅” であることを説明していく。
(Fig.2) 量子コンピューターって 未だに "2つのイオン対" の状態?

実際、 2013 年の今でさえ、彼らが 量子コンピューターと称しているのは たった2つだけで構成された イオン対や 超伝導回路 (= キュービット ) のみなのである。
( たった2つのイオン対のみで コンピューターは どう転んでも作れない。 )
さらに これらのコヒーレント時間 (= 動きがそろった時間 ) は 未だに たったの
84 ミリ秒 (= イオン対の場合 ) や、 500 マイクロ秒 (= 超伝導回路の場合 ) などという 極々短時間のみなのである。
このサイト や このサイト を参照のこと。
さらに 2つのイオン対の動きを揃えるには、ほぼ 絶対零度の 極低温状態が必要不可欠であり、どう転んでも 実際の社会では 使い物にならない産物である。
(Fig.3) 研究者達は 量子コンピューターの実現は すでに諦めている。

最近の様々な論文を見てれば分かるが、物理学者達は 量子コンピューターそのものを実現させようとは まったく考えていない。
つまり 現在の彼らの目的は トップジャーナルに載せて より良いポスト ( もしくは 研究資金 ) をゲットすることのみに特化されていると言っていい。
こういう状況にも関わらず、量子コンピューターの専門家達は "あと数年かそこらで 従来のコンピューターを はるかに上回る速度の 量子コンピューターが実現するだろう。" だとか "今回の研究は 量子コンピューターの実現にとって 大きな一歩である。 " という 魅惑的なフレーズを繰り返すのみである。 しかし 実際には 彼らの心中には このような考えは 微塵も 存在していないと言っていい。
もちろん、トップジャーナルへ載せたり 十分な資金を得ることは 決して悪いことではない。
しかし このことのみが 量子コンピューターの研究の 唯一の動機になってしまっているとすれば これは 深刻な問題 である。
(Fig.4) ブラックホール、超弦理論、標準模型、 スピンホール効果・・・ ← 量子コンピューター ?

実は それほど役に立っていない量子力学が 役に立つと主張するには、 物理学者達は 架空の目標を こしらえる必要がある。
これらの目標の1つとして出てきたのが まさに "量子コンピューター" なのである。
その後、彼らは 様々な分野で この ”量子コンピューター”の用語を 乱用して さかんに唱えるようになった。
( ブラックホール、 超弦理論、標準模型, スピンホール効果、 ベリー位相 までもが 量子コンピューターらしい。 )
10次元の超弦理論までもが 量子コンピューターを利用しようとしている時点で これらの概念が 単なる "ファンタジー" であることが 容易に理解できることと思われる。
(Fig.5) "重ね合わせ" (= 多世界 ) と 超光速の "量子もつれ" ?

"重ね合わせ" (= 多世界 ) と 超光速の "量子もつれ" (= エンタングルメント ) は 量子コンピューターの 核心部分である。
例えば、 Fig.5 では、 ある原子が 2つのエネルギー準位 (= "0" or "1" ) を持つ。
もし この原子が どっちの準位にあるか 分からないとき、物理学者達は この状況を ”重ね合わせ” と表現する。
どっちのエネルギー状態か 分かった瞬間に この重ね合わせ状態は 壊れる (= デコヒーレンス )
要するに、 "重ね合わせ" というのは 単に どちらの状態か 分かっていない状況のことを言っているだけで、奇妙な多世界とは まったく 異なるものである。
例えば、もし この原子が 基底状態 (= "0" ) にあるとき、 光子 (= 光 ) が 空洞内に 放射された後ということになる ( このセクションも参照のこと )。
つまり 空洞内の 光子の有無が 原子のエネルギー状態と関係 (= 量子もつれ !? ) しているという具合である。
しかし、見てのとおり、この状況は 超光速の量子もつれとは 何の関係もない。 しごく当たり前の状況である。
(Fig.6) 超光速の量子もつれの 具体的メカニズムとは 何か?

最も深刻な問題は 現在の物理学者達が この量子もつれのメカニズムそのものの解明を 避けていることである。
それもそのはず、現在の量子論では この量子もつれが 超光速の無気味なリンクによって生じることになっているため、こんなものを 現実の物体を用いて表現することは 絶対に不可能だからである。
つまり、この時点で、科学の発展が 完全に ストップしていると言える。
"科学" というのは 目の前に分からないことがあれば、それに関して 真実を追求し続ける ことに他ならない。
つまり 問うことを諦めるという行為は 科学の精神に完全に 反している。
(Fig.7) 単に 古典的なレーザーで Be+ イオン対を "操作"しているだけ。
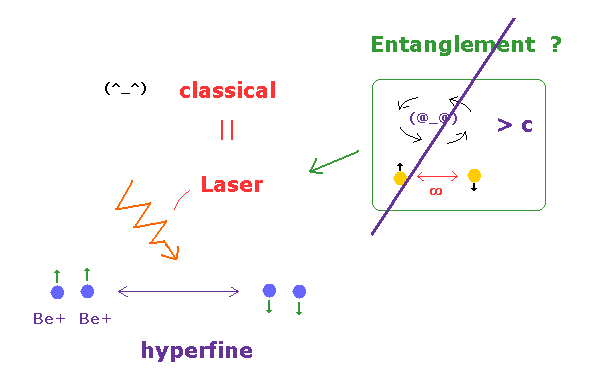
この論文 ( Nature 2001 ) では、2つのベリリウムイオン (= Be+ ) が 互いに量子もつれを引き起こしていると主張している。
しかし 後で説明するが、この量子もつれとは 単に 特定のレーザーによって Be+ のエネルギー準位 (= 超微細構造 ) を"古典的" に操作しているだけである。
照射時間と環境を調節することによって、2つの超微細構造間の遷移を おおよそ コントロールすることができる。
もちろん、このレーザーパルスは 超光速ではないため、量子もつれは これとは 何の関係もない。
実際に 2つのイオン間の距離は たった 3 µm であるため、超光速の相関を証明することは不可能である (= 局所性の ループホール )。
(Fig.8) NMR の量子コンピューターは "量子もつれ" を使用していない。

原子核は 非常に弱い磁気モーメントと持ち、それが周囲の原子と相互作用して 小さなエネルギー準位に分裂する。
彼らは この2つに分裂した微細なエネルギー準位を NMR の量子コンピューターの 量子ビット (= qubit ) として利用して このページに示したように 15 = 5 × 3 の因数分解をした。
しかし実は、これらの NMR の量子コンピューターは 最も重要な "量子もつれ" を使用していないのである。
この論文 (p.4) と この論文に次のようにある。
--------------------------
現在の NMR の実験は 本当の量子コンピューターというよりは、その模擬試験と考えるべきである。なぜなら 量子もつれ現象が まったく現れないからである。
NMR の実験は "separable" すなわち、量子もつれを 起こしていない。
-----------------------------
(Fig.9) 100 億のイオン集団 + "スピンエコー" 信号は 量子もつれとは関係ない。

最近のニュース ( このサイト や このサイト ) では、彼らは 室温で 39 分間もの コヒーレンス時間を実現できたというのがあった。
Fig.23 では "90°パルス" の光が すべてのイオンの核スピンを 横方向に倒す。 (= コヒーレンス状態のスタート。).
徐々に、各スピンが 歳差運動の速度の違いから 異なる方向を向くようになる (= dephase、デコヒーレンス )。
ここで "180°パルス " の光を当てると、それらの位相 (= 歳差運動の方向 ) が ほぼ同じに戻り、延命することができる
重要な点は、この系は 100 億ものイオンを含んでいることである。
つまり これらの非常に多いイオンの ほんの一部のみでも 同じ方向を向いているだけで、スピンエコー信号が検出できて、コヒーレンス状態と認識されるわけである。
つまり この実験は 各イオン対の量子もつれ状態そのものを表しているわけでも何でもないのである。
これは 上記の NMR を使った量子コンピューターと似ている。
つまり この実験は 単に古典力学的な現象なのだが、彼らは 不思議な "量子状態" であると定義したがる。
(Fig.10) "熱雑音" が トンネル効果の原因である。

量子トンネル効果とは、古典的に禁止されている絶縁体などの障壁を 量子力学的な機構によって すり抜ける現象である。
重要な点は このトンネル効果は 非常に薄い わずか 1-3 nm ほどの障壁でしか起こらないということである。
このサイト や このサイトにあるように、非常に低温状態では、トンネル効果は 起きなくなってしまう。
これはつまり "量子トンネル現象" とは 熱雑音 ( や ドブロイ波など ) による 非特異的な 振動効果によって起きることを示している。
(Fig.11) 量子トンネル効果は 古典的な クーロンポテンシャル (= V ) に従う。

クーロンブローケード(閉塞)によれば、絶縁体の容量が小さく、静電エネルギー ( 単一電子による e2/C ) が 温度のエネルギーよりも大きいとき、トンネル効果自体が ブロックされる。
これはつまり "量子トンネル効果" は 古典的なクーロンポテンシャルと 熱力学に 従うことを示している。
つまり トンネル現象を抑制するには 温度を 非常に低く ( ~ mK ) する必要がある。
単一電子が この非常に薄い障壁を通過すると、それは 古典的な電位 V = e/C を生じることになり、これが トンネル効果の抑制につながる (= クーロンブローケード )。
よって、これを打ち消す外電圧をかければ、トンネル効果が起きるというわけである。
このクーロンブローケードの結果は 量子トンネル効果が 単に古典力学的な現象で、奇妙な量子力学的な”幽霊現象”でないことの証である。
(Fig.12) どうして 2つの負の電子が 互いに引き合うの !? →"黙れ !?"

超伝導体では、電子対 (= クーパー対 ) が 格子間隔よりもはるかに長い 数百ナノメーターの距離を挟んで形成されるとしている ( このサイト参照のこと )。
ご存じのとおり、2つの負の電子は 通常 互いに 反発しあう。
2つの電子間の 不自然な引力は 非常に曖昧な 準粒子 "フォノン" によって生じるとされている。
しかし このフォノンは 所詮は 仮想の準粒子にすぎず、科学者達は このフォノンの具体的な正体を 一刻も早く示すべきなのだが、ここで "真理の解明" が ストップしているのが現状である。
困ったものである。
(Fig.13) 量子化されたドブロイ波長。

マイスナー効果のために、超伝導体内部の磁場は 電子の運動 (= ローレンツ力による ) によって打ち消される。
しかし 超伝導体に空いた穴の内部では 磁束量子の整数倍の磁束 ( Φ = n × Φ0 ) が見られる。
(Eq.1)

このページに示したように、現在の量子力学では、この現象は ベクトルポテンシャル "A" の量子化によって起きるとされている。 Eq.1 の "2e" が "クーパー対" というわけである。
しかし 量子論は 現象を抽象化することだけで終わってしまい、肝心な この量子化されたベクトルポテンシャルの正体、メカニズムそのもの に関しては 頑として だんまりを押し通すのみである。
またもや、この時点で ”真理の追求”が止まっていることになる。
(Eq.2)

各電子が ローレンツ力 ( F = evB ) に従って運動しており、かつ その軌道長が ドブロイ波長の
整数倍 と仮定すると、量子化された磁束を 自然に説明できる。
つまり クーロンの法則に 反する クーパー対を 使用する必要がなくなる。
(Eq.3) ← Eq.2

Eq.2 を解くと、 Eq.3 と Eq.4 が得られる。
(Eq.4) ドブロイ波による 磁束の量子化。

Eq.4 にあるように、穴を通過する 磁束 (= Φ ) は 量子化 ( Φ = n × Φ0 ) される。
これが クーパー対に 頼らない 磁束量子の起源である。
(Fig.14) 2つの コンデンサー (= C ) が "架空" のクーパー対の原因。

2つの同じようなジョセフソン結合 (= C ) に挟まれた クーロン島内部では、電荷数が クーパー対のために 2e の整数倍に量子化されると言われている。
この現象は 極超低温 ( ~mK )、超低電圧 ( V → 0 ) などの非常に特殊な状況下でのみで観測される。
重要なことは、これらのサイト ( ここ, ここ, ここ ) にあるように、このクーロン島は 必ず2つのコンデンサーに囲まれているという点である。
後で ( Fig.14 ) 説明するが、これら2つのコンデンサーのために、 偶数の電荷が 必ず必要になってくるというわけである。
これが クーパー対ボックスの トリックである。
(Fig.15) 単に 臨界電流の変化を見ているだけで、重ね合わせは見ていない。

超伝導磁束量子ビットでは、磁束量子の半分の磁束 (= 0.5 × Φ0 ) を与えると、超電流は 時計、反時計両方に流れると言われている。
彼らは この状態は 神秘的な "重ね合わせ状態" (= 2つの互いに逆方向に流れる電流 ) と主張している。
しかし Science や Nature の論文にあるように もちろん、重ね合わせそのものを 観測しているわけではない。( できない。)
マイクロ波を照射後、量子ビット回路の外側を流れる臨界電流の値のわずかな変化を見て、そう判断しているだけである。
この実験は 互いに逆方向の電流によって生じる エネルギー準位の小さな分裂を表しているにすぎない。
また デコヒーレンス ( 作動 ) 時間は 100 mK の超低温下で、わずか 15 ns ( 1 ns = 10-9 秒 ) にすぎない。
これはつまり、この量子コンピューター ( もしあるなら ) は、 たったの 15 ns で 容易に壊れてしまい、まったく役に立たない産物ということになる。
(Fig.16) 位相量子ビットは 単に "古典的に"振動しているだけで、量子もつれでない。

Science によれば、2つの位相量子ビット ( 各々が 2つのエネルギー準位を持つ ) は 量子もつれを起こしているとしている。
しかし 後で説明するが、この量子もつれは 単に 古典的な 振動にすぎず、超光速の無気味なリンクとは まったく異なるものである。
2つの電流回路 ( 量子ビット ) は コンデンサー Cx によって結合している。
このコンデンサーとジョセフソン結合によって、電流と電荷は 2つの量子ビット (= qubit ) 間を行ったり来たりしている ( と言っても たったの 100 ns のみなので、セットアップ後の 単なる 電荷の振動と考えるのが自然である。 )。
この振動状態を "量子もつれ" と主張しているだけで、重ね合わせや 量子もつれそのものを 証明したことにはならない。
また このもつれ状態は たったの 100 ns のため、瞬時に壊れて、まったく 役に立たないことになる。
(Fig.17) 量子コンピューターは 永遠に実現しない幻。

あなた方は 今まで、 " 従来のコンピューターより はるかに速い計算速度を持つ 量子コンピューターは 後 10年かそこらで商用化されるだろう。 " だとか " 量子コンピューターの実現に向けて 大きな一歩を踏み出した。" だとか 在り来たりの文句を 何度も見聞きしてきたことと思われる。
しかし実際は 量子コンピューターの研究は 1982 年の アスペの実験以来 根本的には 何の進歩もしていないのである。
( 検出効率その他が 若干改善されたという程度で、基礎的なメカニズムは 不明のままである。)
すでに述べたように、今現在でさえ、量子コンピューターと称するものは たった "2つのイオン" の状態なのである。
また ほぼ絶対温度の条件が必要で かつ その機能時間は わずか ~ 1 μs と言ったところが限度であり、まったくと言っていいほど役に立たない。
問題は こういう状況での 物理学者達の姿勢にある。
この行き詰まり状態にも関わらず、頑なに 量子もつれそのものの詳細なメカニズムを調べようとはしないのである。
それもそのはず、 超光速の無気味なリンク なんてものを信じている限り、それを実在のもので説明することが 永遠にできないからである。
この状況では 今から 1000年後でさえ、量子コンピューターは 夢の中の 絵に描いた餅状態 のままであることは間違いない。
(Fig.18) Be+ イオン対は 人為的なレーザーで 単に振動しているだけである。

このセクションでは、 この論文 ( Nature 2001 ) の 2つのベリリウムイオン (= Be+ ) 対 間の 量子もつれの詳細なメカニズムについて説明する。
結論から先に言うと、これら2つの Be+ イオンは 単に 制御された レーザーパルスを照射することによって 2つの超微細構造間を行ったり来たりしているだけである。
要するに 超光速の無気味なリンクとは 何の関係もない。
(Fig.19) 原子核と電子の磁気モーメント間による 2つの超微細構造状態

Be+ イオンは 2つの超微細構造のエネルギー準位を持つ。
それらの1つは、原子核と電子のスピンが 同じ方向を向いている。
もう1つの状態では、それらの方向は 互いに 逆方向である。
(Fig.20) 超微細構造は弱すぎて 実用的なコンピューターに使用できない。

もちろん、原子核のスピン磁気モーメントは 非常に弱い。
例えば、 超微細構造 における エネルギー分裂幅は Be+ イオンで 5.17 × 10-6 eV しかないのである。
つまり、 この超微細構造を量子ビットとした量子コンピュターが 仮にできたとしても、 もろすぎて 一瞬で壊れてしまうことは、 誰だって 容易に理解できる。
これが デコヒーレンス ( 作動 ) 時間が いつまでたっても 現実的なレベルに 一向に到達しない要因の1つでもある。
(Fig.21) 2S 状態 (= 角運動量ゼロ ! ) は 非現実的である。

奇妙な量子力学によれば、 "S" 状態は 軌道角運動量が ゼロである。
これはつまり Be+ イオンは 必ず 内殻の 1S の電子群と 原子核に衝突しているのだろうか?
あり得ない話である。
お気づきのとおり、この状態は 非常に非現実的である。
電子スピンも ボーア磁子を持つ。
つまり、超微細構造は 原子核スピンと 電子の軌道運動との相互作用で生じると考えるのが自然である。
(Fig.22) Be+ イオン対は 人為的なレーザーで 振動しているだけである。

この論文 や この論文によれば、彼らは 両方のBe+イオンのスピンが同じ (= ↑↑ or ↓↓ ) になるように 2段階にわたって 十分な時間 レーザー照射をしている。 .
一方だけの遷移の振動数を ずらして 片方のみ (= ↑↓ or ↓↑ ) の遷移が起きることを なるべく 避けようとしている。
つまり 2つの Be イオン間の量子もつれは 単なる人為的なレーザーによる 古典的操作後の状態にすぎないのである。
もちろん、このレーザーの操作は 光速以下であり、実際、このトラップされたイオンの量子もつれには 局所性のループホールが存在し、超光速のリンクが証明されていない。
もし、特定のレーザーパルスを 非常に短時間 (= π/2 pulse ) 照射すると、 2つの状態 ( = ↑↑ もしくは ↓↓ ) が 混ざる確率が ほぼ同じになる。
なぜなら、他のエネルギー準位に移るのには ある程度の時間を 要するからである。
彼らは この混合 (= どっちかまだ測定していない ) 状態を "重ね合わせ" と呼んでいるだけにすぎない。
(Fig.23) "調整した" レーザーが 2つの超微細状態をミックスする。

Fig.22 の量子もつれ状態を用意した後、他のレーザーパルスを当てる。
この照射時間が短いと、それらのいくらかは 同じスピン状態のまま、残りは 他のスピン状態に遷移するよう 分かれることになる。
もちろん、この 位相 φ は 様々な状況に応じて "経験的" な結果から 決定するしかない。
この論文が主張するように、この操作は 純粋に 古典力学的な操作である。
各エネルギー準位を検出するには、このページにあるように、
たくさんの光子を検出する必要がある。
つまり、このケースは 通常の光子対の量子もつれとは
完全に 異なるものである。
Fig.23 を Fig.22 に代入して、次を得る。
(Eq.5)

と
(Eq.6)
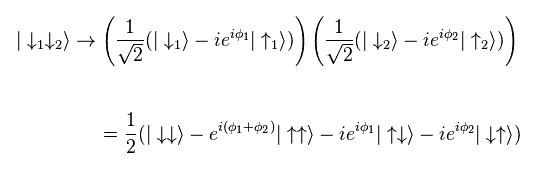
Eq.5 と Eq.6 を用いると、 Fig.22 の量子もつれ状態は 次のように変化する。
(Eq.7)

ここでは このページにあるように CHSH タイプのベルの不等式を計算する。
この不等式では、最初に 次の引き算をする。
2つの粒子の状態が同じ確率 (= ↑↑ + ↓↓ ) - 2つの状態が 異なる確率 (= ↑↓ + ↓↑ )。
(Fig.24) CHSH のベルの不等式の計算。

Eq.7 の各係数から それぞれの状態の 確率 (= P ) が分かる。
(Eq.8)

と
(Eq.9)

ここでは次を用いた。
(Eq.10)

Eq.8 と Eq.9 より、
(Eq.11)

ここでは 次を用いた。
(Eq.12)

例えば、彼らは 次の位相 ( このケースでは "照射時間" に相当する ) を用いた。
(Eq.13)

Eq.13 を使って、例えば次の値は、
(Eq.14)
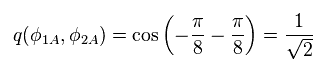
結果、4つの異なる種類も計算して、
(Eq.15)

このベルの不等式は 古典的な限界 "2" よりも大きくなってしまった。
そのため 彼らは これら2つの Be+ イオン対は 超光速の量子もつれ状態にあると主張し始めたのだ。
しかしもちろん、この計算には ある トリックが隠されている。
つまり 超光速の無気味なリンクは 単なる 幻想にすぎない。
(Fig.25) 各状態の確率。

ここで まず Fig.22 の中の ↑↑ の状態 (= 右辺の 1項目 ) のみ考えてみる。
Eq.5 から、Fig.25 に示したように 各状態の確率を知ることができる。
ご覧のとおり、すべての確率は 同じ "1/4" になる。
(Fig.26) ↑↑ のみある時 = 量子もつれはなし。

Fig.25 の確率を用いると、Fig.26 に示したように CHSH の結果は "ゼロ" ( cosine ではなく ) になる。
これはつまり ↑↑ か ↓↓ のどちらか 1つのみしかない時、ベルの不等式は 破れない ( = 古典的 !? ) のである。
ここに 重要な トリックがある。
(Fig.27) "1" = 初期状態が1つ "2" = 初期状態が2つ。
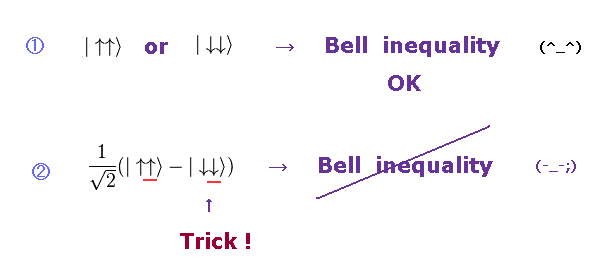
ベルの不等式は 純粋に古典的な確率に基づいている。そのため それが破れることは 非古典的ということになる。
古典力学によれば、初期状態は 確率 × 確率 × 確率... のように変化する。
もし 初期の状態が たった ↑↑ しかないとき、この確率の関係 (= Fig.28 ) は 正確に成り立つ。
これはつまり ベルの不等式は 破れない。
(Fig.28) 確率の関係。

しかし もし Be+ のスピンの初期状態が もう1つの Be+ のスピンに 応じて 変化すると、これはつまり 2つの混合した初期状態ということになる。
この混合した状態は ベルの不等式を破っても不思議ではないのである。
なぜなら Fig.28 の表は 1つの共通の初期状態を 前提条件にしているからである。
つまり このケースは ベルの不等式を破ってはいるが、 量子もつれ とは何の関係もなく、単なる
古典的な状態にすぎない。
このセクションに示したように、 彼らは ベルの不等式を
間違った状況に 誤使用しているにだけである。
( これはつまり ベルの不等式は このケースでは 使用できないことになる。 )
(Fig.29) 原子のエネルギー準位と 空洞内の光子の関係。

このサイトにあるように、原子が 空洞共振器 (= cavity ) 内の光子と 量子もつれを 起こし得ると言われている。 .
リュードベリ原子の最外殻電子は 非常に大きな主量子数 ( n = 20 ~ 40 ) を持つ。
つまり、このリュードベリ原子は 非常に不安定な状態なのだが、彼らは この原子を量子もつれの研究にさかんに利用しようとしている。
空洞共振器 ( cavity-QED ) とは 反射鏡に囲まれた空洞内に ある振動数の光を 閉じ込める機器である。
Fig.29 左図では、原子の主量子数 (= エネルギー準位 ) は "n" で、 光子1つ (= 非常に弱い光 ) が 空洞内に閉じこめられている。
Fig.29 右図では、このリュードベリ原子が この光子を吸収して、n+1 のエネルギー準位に 励起されている。
つまり 空洞内には 光子 (= エネルギー ) は残っていない。
(Fig.30) 量子もつれは 本当か?

よって、物理学者達は 原子のエネルギー準位 (= n もしくは n+1 ) と 光子数 (= 0 もしくは 1 ) が 奇妙な 量子もつれ状態にあると 主張しだしたのである。
ご覧の通り、現在の量子力学には すべての事象を "ファンタジー" の量子もつれに 無理やり 結びつけようとする意志が ありありと見られる。。
(Fig.31) NMR の 90o (= π/2 )、 180o (= π ) パルス。

"π/2"、 "π" パルスは 元々 NMR で使用されていた用語である。
このサイト や このサイトにあるように、ある特定の振動数のパルスを 原子核スピンに当てると、このスピンの方向が 変化する。
もちろん、各原子核のスピンの向きを 完全に逆転には 少し時間が かかる。
このパルスを 非常に短い時間だけ当てると、スピンは 外磁場に対して 水平方向に向く。
このパルスの 照射時間 のことを "π/2" パルス と呼ぶ。
このパルスを照射する時間を 2倍にすると、原子核スピンは 完全に 逆転させることができる。
この時の照射時間を "π" パルス と呼ぶ。
彼らは このロジックを 一般的な ラビ振動 まで 拡大解釈させた。
(Fig.32) レーザーパルスは エネルギー準位を変化させる。

ここで リュードベリ原子に また戻る。
Fig.32 では、原子を パルスレーザーで照射すると、そのエネルギー準位が "n" と n+1" の間で 振動する (= ラビ振動。 "誘導"放射も含めて )。
彼らは この振動を "重ね合わせ" (= 多世界 !? ) と表現してしまったのである。
このサイトにあるように、ラビ振動における "時間" と "位相" の関係は 一定の周期・規則に従った 正弦曲線を示す。
"重ね合わせ" とは、 まさに "神がサイコロを振る"状態であり、 ランダムに どの状態を与えるかが決まるはずなのだが、明らかに ラビ振動は 規則正しく変化しており、この定義と矛盾している。
つまり "重ね合わせ" という名前は 非常に不適切と言える。
(Fig.33) π/2 と π パルス の関係。

基本的に、 π/2 パルスの 照射時間は π パルスの 半分である。
原子に パルスを ある十分な時間 (= π パルス ) 当てると、そのエネルギー準位が 完全に逆転することになる。
( この照射時間は 他の状況を考慮して 人為的に調節する必要がある。)
つまり 照射時間が π パルスの 半分 ( 1/2 × π ) だとすると、エネルギー準位が 変わる確率は 約 50 % ということになる。
見てのとおり、これらの現象は 古典的に見て まったく不思議ではないが、物理学者達は この混合状態を "重ね合わせ" と呼びたがる。
(Fig.34) 空洞内に 光子があると、 エネルギー準位は "n" に落ちる。

Fig.34 では、この原子が 光 (= 光子 ? ) を 空洞内に放出して, 基底状態 (= "g" = "n" ) に落ちると、この放出された光子は 空洞内に留まることになる (= "1" )。
(Fig.35) 光子が 原子に吸収されると・・ ..

Fig.35 では、この放出された光子が 再び 原子に 吸収されている。
結果的に、この原子は "e" (= n+1 ) の準位に 励起されて、空洞内には 光子は 残ってないことになる。
(Fig.36) 量子もつれ !?

つまり 現在の量子力学によれば、Fig.34 と Fig.35 の2つの状態は 原子と光子が 量子もつれ を引き起こした状態ということになる。
原子が 励起される (= "e" ) と、光子は 残っていない ( "0" ) → よって "e" - "0" が もつれている。
ご覧のとおり、これらの状態は 古典的な視点からして 極 自然に説明できる。
奇妙な "重ね合わせ" や "量子もつれ" などという概念は まったく 不要である。
(Fig.37) ハミルトニアン。

これらの状態のハミルトニアンを しばしば Fig.37 のように表す。
生成 (= a† )、 消滅 (= a ) 演算子は "光子"を表す。
"σ" は 原子のエネルギー状態。 パウリ行列で表現している。
あらゆる物を スピンの方向と 関連させようとしているわけである。
(Fig.38) 時間発展。

ハミルトニアンは 時間発展の役割を果たす。
Fig.38 にあるように、 π/2 と π パルスは ある時間後の 位相の変化を 表わしている。
(Fig.39) LC 回路における 電荷 Q と 電流 I。

このセクションでは、1つのコイル ( インダクタンス L ) と 1つのコンデンサー ( 容量 C ) で構成された 単純な LC 回路について考える。
このサイト や このサイト 参照のこと。
Fig.39A では、電流 I は ゼロで、コンデンサー C には 電荷が フルに蓄えられている (= 最大電荷、Q0 )。
電流の時間的増加によって コイルには 電圧 ( V = LdI/dt ) が発生する。
Fig.39C では、電流が 最大値 (= I0 ) をとっている。
この状態では、コンデンサーと コイルにおける電圧は 両方ゼロである。
ご覧のとおり、LC 回路では 電荷と電流は 常に 振動しているのである。
(Eq.16) 電圧の関係。

コンデンサーの電圧は "Q/C" である。
つまり Eq.16 の関係式を満足する。
(Eq.17)
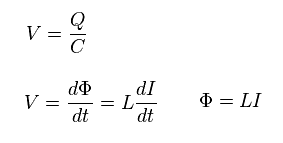
Fig.17 では、 Φ は コイルを貫く 磁束を表す。
この磁束の変化によって 電圧が生じる。
(Eq.18) 全エネルギー。
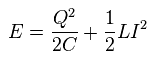
LC 回路の全エネルギーは Eq.18 のようになる。
Fig.39A と C における 全エネルギーは 次のように表せる。
(Eq.19) 全エネルギー。

電流 I は 電荷 Q の時間微分と等しい。
つまり Eq.16 は
(Eq.20)

Eq.20 の解は、
(Eq.21)

この ω は LC 回路の振動数になる。
しかし たった一種類の ω しかないので、 この単純な LC 回路は 量子ビット として使えない。
このサイト (p.3) には以下のようにある。
-----------------------------
超伝導 LC 回路は 量子ビットとして 機能しない。なぜなら それは 無限の等間隔のエネルギー準位が 存在している状態のため、その中から 特定の2つの準位をピックアップできないからである。
-----------------------------
(Fig.40) ジョセフソン結合のモデル。

ジョセフソン接合は 非常に薄い絶縁体 ( ~ nm ) を挟んだ 2つの超伝導体から成る。
ここを流れるジョセフソン電流の変化は 磁束量子 (= Φ0 ) に関係していることが分かっている。
しかし 現在の量子力学は ジョセフソン接合内の 詳細なメカニズムそのものの説明を避けている状態である。
電流が 超伝導体内部に磁場を引き起こすことを思い浮かべてみる。
マイスナー効果によって、この電流は 超伝導体内の電子の動きによって 追い出されることになる。
この電子の動きは ドブロイ波を生じ、かつ それが量子化される傾向にある。
これが 磁束量子の起源であり、超電流の振動に 深く関係していると言える。
(Eq.22)

Eq.22 は ジョセフソン超電流 I(t) である。
超伝導体内部の 磁束 Φ は 直接観測できない。
( 電圧 V のみ測定できる。 )
(Eq.23)

ジョセフソン接合は コイルとしての性質も持つ。
ただ、Eq.23 の インダクタンス L は 常に変化しており、ここが 単純な LC 回路と異なる部分である。

Eq.23 と Eq.24 を用いて、全 ジョセフソンエネルギー (= EJ ) を得ることができる。
(Eq.25)

ここでは
(Eq.26)

回路が ジョセフソン接合 (= CJ ) と コンデンサー (= Cg ) で構成されているとすると、
(Fig.41)

全エネルギーは 次のようになる。
(Eq.27)

ここでは
(Eq.28)

"Ng" は クーパー対 (= 2e ) の数と 彼らは主張している。
(Fig.42) クーパー対 (= 2e ) が ジョセフソン接合を通過する !?

BCS 理論 によれば、2つの負電荷の電子が 超伝導体内で くっついて クーパー対を形成することになっている。
しかし 仮想の準粒子 フォノン に問題を投げかけたままで、肝心の具体的なメカニズムは 謎 のままである。
(Fig.43) 単一接合のクーロン島。

この論文 (Nature) では、超伝導体内部の クーロン島の 蓄積電荷は 2e (= クーパー対 ? ) の整数倍に量子化されるらしい。
しかし この状況にするには 電圧 U や 温度を 非常に 低くしなければならない ( ← かなり 特殊な状況である。 )
このサイト (p.11) にあるように、ジョセフソン接合 (= CJ ) と コンデンサー (= Cg ) の静電容量は ほぼ同じに調整してある。
(Fig.44) 2e 周期性 ?

Fig.44 では、横軸が コンデンサーの 電荷 Q、縦軸が、クーロン島に蓄えられた 全電荷であると 彼らは主張してある。
しかし もちろん、クーロン島内の 電荷数を直接観測することは不可能である。
(Fig.45) 単一電子トランジスタ ( SET, electrometer )。

Fig.45 では、 electrometer が 小さなコンデンサー Cc を介して クーロン島に接合されている。
クーロン島内の 電位の変化は この electrometer の電流に 影響を与える。
この機構を通じて、Fig.44 のように "2e 周期性" が 観測されたというらしい。
Fig.43 から、全電圧 U は 次のように表せる。
(Fig.46)

Fig.44 の Q が "1" のとき、この電圧 U は 次のようになる。
(Fig.47)

Fig.46 から Fig.47 の電圧が 実質 不可能であることが分かる。
(Fig.48)

Fig.48 に示したように、この系には 2つ ( 1つでなく ) の コンデンサー (= CJ と Cg ) がある。
つまり 最小の "有限な" 電圧 U は 次のようになる。
(Fig.49)

Fig.49 は Fig.47 と 矛盾している。
これはつまり クーパー対とは クーロン島の両端の 2つのコンデンサーによって生じた "架空" の産物であることになる。
(Fig.50)
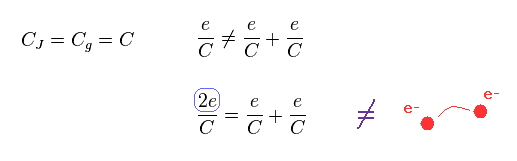
つまり トリック は この 2つのコンデンサーにある。クーパー対でなく。
(Fig.51)

(Fig.52) クーロンブロッケード electrometer のクーパー対?

Fig.52 は 2つのジョセフソン接合 ( 容量 C ) と 1つのコンデンサー ( Cg )で挟まれた クーロンブロッケード electrometer である。
この論文 (Fig.2) と この論文にあるように、電流 I は V → 0 の極限で 2e 周期性 を示す。
そのため 彼らは この 2e 周期性の電流は クーロン島内の クーパー対を表していると主張している。
しかし 再び、 このトリックは 2つの同一の ジョセフソン接合コンデンサー (= 2 × C ) にある。
(Fig.53) Cg に 1つの電荷 (= e ) のみがあるとき。

Fig.53 では、 コンデンサー Cg に 1つの電荷のみが 蓄積されている ( CgVg = e )。
このケースでは、Fig.53 に示したように、クーロン島内の電荷は 不安定になってしまう。
(Eq.29)

(Eq.30)

ここで A と B の電位はゼロである ( V = 0)。
もし 単一の電荷のみが どちらか1つの接合部のみにあるとすると、電位 A と B は、Eq.29 と Eq.30 に示したように 同じにはなれない。 矛盾した状態である。
(Fig.54) 偶数個の電荷が Cg に蓄積 ← クーパー対 !?

もし 偶数個の電荷が Cg に蓄積されていると、電位と電荷の関係は 矛盾なく 安定になる。
この機構が 2e 周期性の電流変化の原因である。 ここには クーパー対は まったく関係していない。
(Eq.31) 偶数個は OK。

この結果は (バイアス) 電流の 2e 周期性は クーパー対でなく、2つの同一の接合コンデンサーによって生じていることを示している。
この バイアス電圧が 少しでも 大きくなると、準粒子汚染というのが起きる。
端的に言うと、普通に 1e 周期性 に 簡単に移行してしまうことである。
つまり "2e 周期性" というのは 非常に特殊な状況のときのみ 起きうることになる。
(Fig.55) "クーパー対" は 接合を行ったり来たり?

この論文 (Nature) では、1つのクーパー対が クーパー対ボックス内を 振動していると主張している。
もちろん、クーパー対そのものを 直接観測することは 不可能である。
彼らは 検出器での ある電流の変化を観察しているだけである。
上で述べたように、Fig.55 のクーロン島は 2つの同一のジョセフソン接合で囲まれている。
これが "電荷の振動" が見られる理由の1つである。
(Fig.56) パルス電圧が "古典的" ( クーパー対でなく ) な電荷振動を起こす。

彼らは クーロン島に 短い電圧パルス を当てた。
このサイト (p.33) にあるように、このクーパー対崩壊を 検出することは 不可能 である。
この振動を 繰り返すことによって、十分な電荷を貯めてから、測定するという作業をしている。
(Fig.57) 振動時間は たったの 2 ns ?

この論文によれば、振動時間は ほぼ絶対零度 (= 30 mK ) で たったの 2 ns である。
つまり この電荷量子ビットを 実用的な量子コンピューターとして利用することは まず
不可能である。
(Fig.58) 電荷は 古典的に振動している。

Fig.58 に示したように、たった1つの電荷が コンデンサーに溜まっているとしたら ( Q0 = e )、2つの接合部の電位は 同じでなくなる。
この状態は 不安定で矛盾している。
つまり、これらの電荷は 振動し始める。
もちろん、ジョセフソン接合そのものも 電流の振動の原因になる。
つまり フォノンやクーパー対を使用する必要がなくなる。
(Fig.59) 電荷の電位エネルギー。y.

Fig.59 は クーロン島での 電荷の電位エネルギーである。
(Fig.60) 蓄積した電荷。

(Fig.61)

もし 蓄積した電荷 Qt が "1" のとき、 2つの接合は 不安定になり、これが電荷の振動を引き起こす。
これがトリックである。
(Fig.62) 電荷の量子ビット パート II。

この論文 (Science) では 別の 電荷量子ビットを紹介している。
この実験においても、クーパー対自体を 直接観測してはいない。
もちろん、重ね合わせ、すなわち 多世界自体を 見ることも 不可能である。
(Fig.63) クーパー対の "間接的" な観測?

パルス電圧 u(t) を照射すると、回路の電荷は 振動し始める。
これも 古典的な振動で、 重ね合わせとは まったく異なる。
その後、検出用電流 I(t) を当てて、電圧 V(t) の 変化を検出しているだけである。
この電圧の振幅が ある閾値を超えたときを "クーパー対" であると仮定しているだけである。
これも単に推測にすぎない。
(Fig.64) 磁束量子ビットのメカニズム。

超伝導の磁束量子ビットにおいては、磁束量子の半分 (= 0.5 × Φ0 ) の磁場をループ部分に当てると、2つの逆向きの電流が生成される。
Fig.64 上図にあるように、 0.2×Φ0 の磁束を当てると、電子は 磁場を キャンセルして ゼロにしようとする。
しかし、 0.8×Φ0 の磁束を当てると、 "1×Φ0" の磁束のほうが、最初の磁束に 近くなる。
結果的に、電子は この磁束を 1×Φ0 まで、増加させる。
(Fig.65) 2つの逆の電流の "重ね合わせ" !?

0.5 × Φ0 の磁束を ループ部分に当てると、2つの 量子化された状態が縮退する。
結果的に、互いに逆向きの電流が 同時に生成される (= 重ね合わせ !? ) と主張している。
しかし、もちろん、この奇妙な重ね合わせを 直接観測することは できない。
これもまた 単なる推測にすぎない。
(Fig.66) 磁束量子ビットと SQUID。

この論文 (Science) では、内側の回路は 磁束量子ビットで、2つの逆の電荷が 流れている。
また 外側の回路 (= DC-SQUID ) は 間接的な検出器として 使われる。
もし バイアス電流 I が ある臨界点よりも大きいと、電圧 V が検出される。
(Fig.67)

彼らの主張によれば、マイクロ波が これらの回路に当てられると、Fig.67 で 曲線に 凹凸がみられる。
この 凹凸は 電流の方向が変わったことによるエネルギー変化と言われている。
0.5 × Φ0 の地点では、2つの状態が 縮退している (= エネルギー差がゼロ ) ため、これら凹凸が見られない。
彼らは Fig.67 のグラフを "重ね合わせ" と呼んでいるが、もちろん 重ね合わせそのものを見ているわけではない。
(Fig.68) 非常に弱い量子ビット。

この磁束量子ビットのデコヒーレンス時間は 100 mK で たったの 15 ns である。
またもや、この超伝導量子ビットは 完全に 非現実的である。
(Eq.32)

このサイト や このサイトにあるように SQUID は 2つのジョセフソン接合で構成されている。
同じ方向の電流が これらの接合を通っている。
結果的に、全電流 I は
(Eq.33)

ここでは
(Eq.34)

Eq.33 と Eq.34 から、次を得る。
(Eq.35)

(Fig.69) 位相量子ビット A と B が 量子もつれを起こしている !?
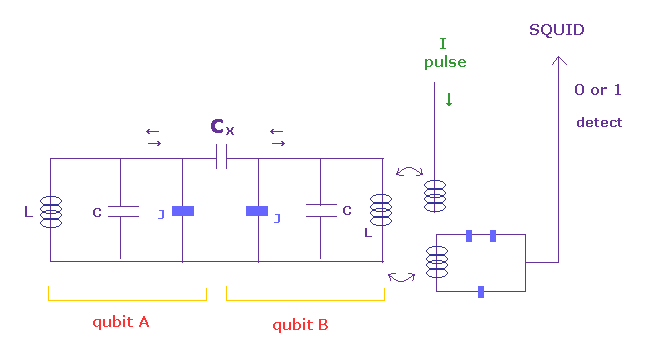
位相量子ビット ( Science ) では、 コンデンサー 、 ジョセフソン接合、コイルなどで生じた 非常に小さなエネルギーの分裂を利用している。
単純な LC 回路と異なり、ここには 多くの種類の振動数が含まれている。
よって それらのうちの特定の光の振動数を利用することによって、特定のエネルギー状態を
コントロールすることができる。
彼らは 2つのエネルギー準位を 量子ビット (= "0" or "1" ) として用いている。
もちろん、これらのエネルギー準位は 人為的に設定されたものである。
様々な電流 I や 電圧を調節することによって、これらの振動数をコントロールすることができる。
(Fig.70) 古典的な振動数 = 量子もつれ。

回路 (= qubit ) の1つに マイクロ波を照射すると、そのエネルギー準位が上がる ( "0" → "1" )。
2つの回路を コンデンサー Cx で繋げることによって、各電流とエネルギー準位は 2つの回路間を振動する ( 非常に短い時間だけであるが・・ わずか 100 ns )。
回路の1つのエネルギーが "0" (= 基底状態 ) のとき、もう1つの回路は エネルギー保存則により "1" になる。
彼らは この "01" もしくは "10" の関係を "量子もつれ"と呼んでいる。
しかし、この結果は 単に 古典的な 電流の振動を示したにすぎない。
(Fig.71) 非常にもろい量子ビット。

この位相量子ビットのデコーヒレンス時間は 25 mK で、わずか 100 ns しかない。
つまり この超伝導量子ビットは 現実のコンピューターにまったく応用できないことが分かる。
(Ap.1) Be+ イオン対の 確率表 ?

ベルの不等式を満足するには、Ap.1 の確率表が成り立たなければならない。
Ap.1 では、4つの変数 (= φ1A, φ1B, φ2A, φ2B ) を決めると、各確率 ( 例えば "P5" ) は 1つの値に決まる。
しかし 上の Be+ イオンのケースでは、この P5 は 1つに決まらない。
なぜなら、それは 混合した初期状態を持っているからである。
(Ap.2) "P5" 確率は "1つに" 決まるのか?

確率 P5 は 2種類の方法 (= ① と ② ) で表せる。
もちろん、Ap.1 と ベルの不等式を満たすには、これら2つの P5 が同じになる必要がある。
(Ap.3)

しかし 上の Be+ のケースでは、これら2つの P5 は まったく異なる値を与える。
(Eq.8)

(Eq.9)

Eq.8 と Eq.9 を用いると、最初の P5 (= "1" ) は 次のようになる。
(Ap.4)

ここでは、次の条件を用いる。
(Ap.5)

Ap.5 を Ap.4 に代入して、次を得る。
(Ap.6)

ここでは次を使う。
(Ap.7)

Ap.2 で 2つめの P5 (= "2" ) は、
(Ap.8)

Ap.5 を Ap.8 に代入して、次を得る。
(Ap.9)

Ap.6 (= 1" ) と Ap.9 (= "2" ) を比較すると、2つの種類の P5 が 異なることが分かる。
(Ap.10)
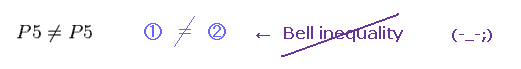
これはつまり Ap.1 の表が 定義できないということになる。
つまり、ベルの不等式が 破れている。
しかしもちろん、このイオンのケースでは 超光速の量子もつれは 何の関係もない。
彼らは ベルの不等式を 間違った例に使用しているだけである。

2014/4/16 updated This site is link free.