
トップページ (正確な新ボーア模型)
量子コンピューターは 実現しない。
電子スピンは 幻想である。
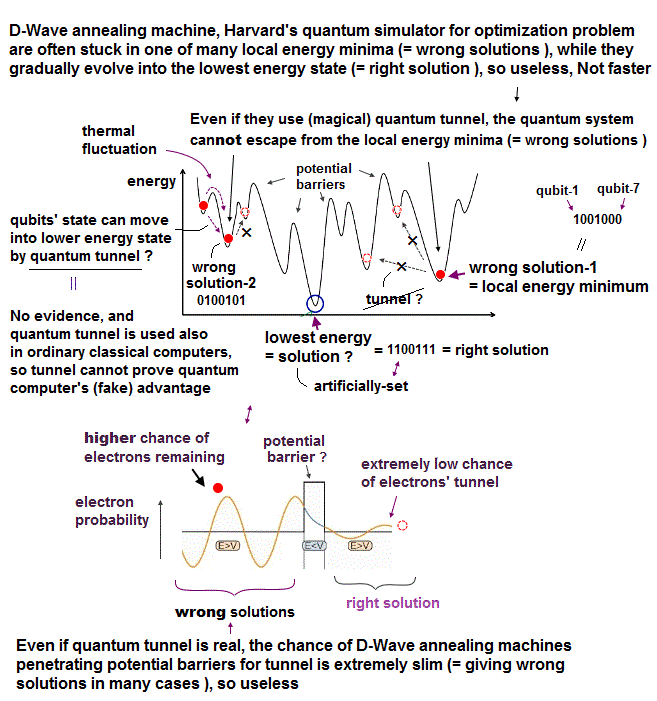
(Fig.1) トンネル効果に基づく D-Wave の量子コンピューターは 本当か?

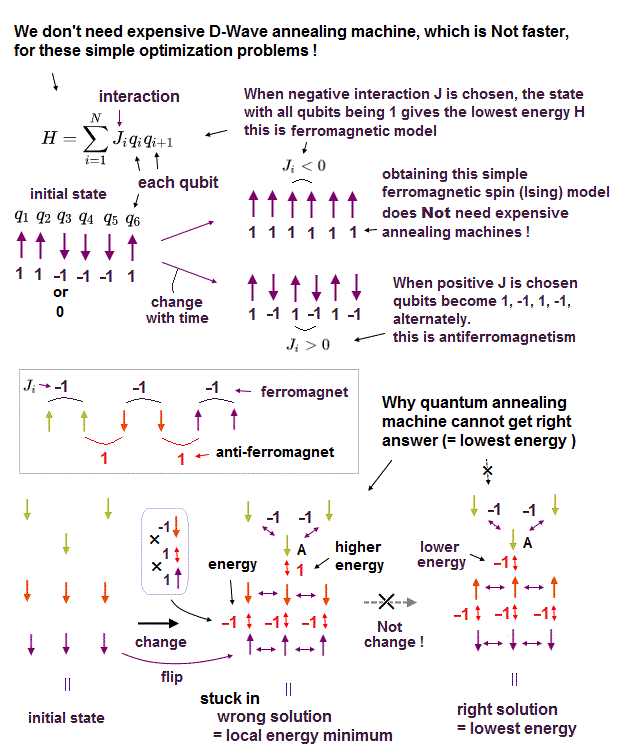
最適化 ( セールスマン ) 問題においては、 いろんな町を結ぶ通路の中で 最短経路を探すのに すべての町 をめぐって あらゆる可能性を 調べつくす必要があるため、膨大な時間がかかりすぎることになる。
512 量子ビットを持つ D-Wave の量子コンピューターは 量子トンネル効果 や アニーリング (量子焼きなまし法) によってこの問題を 高速で解決できると言われている。 このサイト や このサイト を参照のこと。
量子アニーリング とは 量子トンネル効果を用いて たくさんある候補の中から もっとも最少のエネルギー状態を探しだす手法である。
この D-Wave の量子コンピューターは 量子もつれの機構に頼っていないため、通常の量子コンピューター (= 実用化されていない ) とは異なる。
(Fig.2) D-Wave は 通常のコンピューターより速くない。

このニュース ( または ここ ここ ) によれば、最新の研究で D-Wave の量子コンピューターは 実は 従来の古典的なコンピューターよりも 速くない ことが 独立したチームによって それぞれ実証された。
結果は Science に掲載された。
D-Wave は 現在 唯一の商用の量子コンピューターであるため、この実験結果は 今のところ 現実の世界では 量子コンピューターなるものの証拠が まったく存在しない ことを示したことになる。
(Fig.3) D-Wave の トンネル効果 は 本当に 量子力学 ?

D-Wave が "量子コンピューター" と呼ばれる所以は 量子トンネル効果 にあると言っていい。
この 量子トンネル効果は 古典力学では禁止されている ポテンシャル障壁をもすり抜ける現象と言われている。
問題は D-Wave の量子コンピューターが 本当に 量子力学的効果のみに基づく 量子トンネル効果に 依存しているかどうかという点である。
ここで "量子力学的" という言葉の定義 が いったい何なのかということになる。
このページでは 彼らが主張する 量子力学的な 障壁というものが 現実的な意味での 古典力学的な現象で 置き換えられる ことを示す。
(Fig.4) ジョセフソン電流 I(t) の 正弦曲線 を引き起こす原動力とは?

ここ、 ここ、 ここ (p.4) にあるように、ジョセフソン結合を通る電流は それを貫く 磁束 (= Φ ) に応じて 周期的に変化する。
(Fig.5) ドブロイ波長 (= 磁束量子 ) の 整数倍。

超伝導回路のループを貫く磁束は 磁束量子の整数倍 ( n × Φ0 ) になる傾向がある。 このセクションも参照のこと。
量子力学は 得てして この磁束量子の起源の解明を 避ける傾向にあるが、この現象が ドブロイ波の式に関係していることは 一目瞭然である。
このサイト や このサイト (p.23) を参照のこと。
このドブロイ波に基づく 電流の sin 曲線こそが D-Wave の量子トンネル効果に関連づけられる ポテンシャル障壁 の起源である。
(Fig.6) ファラデーの法則による 誘導起電力 V。

ファラデー・レンツの電磁誘導の法則によれば、 貫く磁束 (= Φ ) が 時間と伴に変化するとき、導線に沿って 誘導起電力が生じる。
この誘導起電力は 磁束の変化を妨げる向きの 電流を生じさせる。
(Fig.7) 電気ポテンシャルの時間変化 = V × I.

電気 (= クーロン ) エネルギーの時間変化は 電圧 V × 電流 I で与えられる。
( 電流 I とは 単位時間に流れる電荷量である。 )
重要な点は 彼らは クーロン (= ジョセフソン ) ポテンシャルの計算の際に Fig.4 の特殊な電流の形式を用いていることである。
すでに述べたように、この特殊な電流 I の 正弦曲線の起源は 通常の電気力によるものではなく、ドブロイの関係式に基づくものである。
つまり 正確な全エネルギー (= ポテンシャル障壁? ) の導出の際には クーロンエネルギーのみでなく、他の効果、いわゆるドブロイ波によるエネルギーも足し合わせる必要がある。
(Fig.8) ジョセフソンエネルギーの計算で ドブロイ効果を無視。

このサイト や このサイト にあるように、彼らは ジョセフソンエネルギーを得るときに クーロンの関係式のみに 頼っている。
つまり 全エネルギー (= EJ ) は I V (= 電流 × 電圧 ) を 時間 t で積分して得られるというわけである。
しかし この計算は明らかに矛盾している。
なぜなら ジョセフソン電流 I の 正弦曲線 ( 磁束に依存 ) は 通常のクーロン相互作用以外の 別の効果によって生じているからである。
つまり、クーロン以外の別の力 (= ドブロイの関係式による ) も考慮しないと 真のポテンシャルを計算したことにならないわけである。
(Fig.9) ソレノイドにおける 通常の磁気エネルギー。

電流のループは インダクタンス L のソレノイドの性質を持つ。
このサイトにあるように、 磁場に蓄えられたエネルギーは Fig.9 で与えられる。
このループを貫く磁束 (= Φ ) は "LI" (= インダクタンス × 電流 ) に等しい。
(Fig.10) 全エネルギー = ジョセフソン + 磁気エネルギー?

Fig.8 (= ジョセフソンエネルギー ) と Fig.9 (= 通常の磁気エネルギー ) の効果を足すと、Fig.10 のような全エネルギーが得られる。
ΦX は 外部のソース由来の磁束で、全磁束の調整に使用される。
この ΦX が 磁束量子の半分 (= 1/2Φ0 ) のとき、エネルギーは次のようになる。
(Fig.11) 全エネルギー?

ジョセフソンエネルギーの コサインカーブが 所謂 2つの井戸型ポテンシャルの 主要な要因である。
Fig.12 や このサイト (p.9) を参照のこと。
(Fig.12) ポテンシャル障壁の起源は いったい何か?

Fig.11 と Fig.12 にあるように、位相 θ が 0 と 2π ( Φ = 0 と Φ0 ) のとき、全ポテンシャルエネルギーは 最も低くなる。
磁束の違いは ジョセフソン電流が 時計、反時計方向に流れることによって生じる。
彼らの主張によれば、これら2つの互いに逆方向の電流は 重ね合わせ状態にあり ( ΦX = 1/2Φ0 のとき )、それが 量子コンピューターの量子ビット (= qbit ) として使用できるとしている。
(Fig.12') 反時計方向の電流 = スピンアップ ? 時計方向 = スピンダウン ? ← 重ね合わせ ?
もちろん、多世界様の重ね合わせという概念は 完全に非実在的である。
これらの状態は 単に 電流 I の向きが 2つの向きの状態に同じ確率でなりやすいことを示したにすぎない。
要するに、この現象は 何か未知の力が働いて、磁束を 磁束量子の整数倍 (= n × Φ0 ) にさせようとしていることを意味している。
(Fig.13) ファラデーの法則は 元の磁束を保とうとする。

古典的なファラデーの法則は 元の磁束を一定の値に保つように働く。
つまり 磁束が 元の 1/2Φ0 から 減少するとき、誘導起電力は 磁束を元の状態に 増加させようとする。
つまり 通常の電磁気学によれば、元の 1/2Φ0 の状態が一番安定ということになる。
(Fig.14) ファラデーの法則は 磁束の増加を妨げる。

磁束が 元の 1/2Φ0 から 増加するとき、誘導起電力は 磁束を減少させる方向に生じる。
結果、通常の電磁気学のみが関係しているとすると、元の磁束 1/2Φ0 の状態のポテンシャルエネルギーが最も低くなることになり、2つの井戸型電位 (= double-well ) は 生じないことになる。
(Fig.15) 井戸型電位 (= 障壁 ) は ドブロイ効果によって生じる。
D-Wave の量子コンピューターでは 超伝導回路で、量子トンネル効果により 2つの井戸型ポテンシャルの障壁を 通過できるとしている。論文 ( Nature ) 参照のこと。
しかし Fig.8 にあるように、もともとドブロイ効果によって正弦曲線ができているにも関わらず、 ポテンシャル障壁の計算に クーロンの関係式 (= 電流 × 電圧 ) しか用いていないのである。
これは 明らかに 自己矛盾である。
(Fig.16) ドブロイ波長の整数倍が 井戸型電位の起源。

Fig.5 と このセクションで述べたように、ジョセフソン ( 超伝導 ) 電流は 整数倍の磁束量子 (= Φ0 ) を生じるように流れる傾向にある。
つまり 磁束が 元の 1/2Φ0 より増加すると それに拍車をかけて さらに増加させて 1 × Φ0 の磁束になろうとする。
もちろん この駆動力は 従来のファラデーの法則によらないことは言うまでもない。
なぜなら 元のファラデーの法則は 電流の増加を抑える方向に働くからである。
要するに この時点で 通常のクーロン障壁とは 別のポテンシャルの存在を考えなければならないのである。
(Fig.17)

Fig.17 にあるように、従来の電磁気のみが 超伝導回路に関係しているとしたら、2つの井戸型ポテンシャル自体が そもそも 形成されない。
なぜなら 磁気エネルギーは 磁束の2乗 (= Φ2 ) のみに比例しているからである。
(Fig.18) ドブロイ効果が主要な要因。.

Fig.18 では、磁束が 元の1/2Φ0 から減少するとき、 さらに減少して 0 × Φ0 (= 整数倍の 磁束量子 ) の状態になろうとする。
すでに述べたように、この効果は 通常の電磁気力 ( ポテンシャル ) で説明することができない。
(Fig.19) クーロン電位 (= 障壁 ) 以外の効果を考慮する必要がある。

しかし 正弦曲線状のカーブを示すジョセフソンエネルギー (= EJcosθ ) の計算の際に、彼らは それに伴う通常の電磁気学のみ (= 電流 I × 電圧 V ) の 関係式に頼っているのである。
超伝導量子ビットでは、Fig.19 の関係式に基づいて 量子トンネル効果の正当性を主張している。
しかし Fig.19 は 本当のポテンシャルを反映していない。なぜなら ドブロイなどの他の効果を含んでいないからである。
この論文 ( Science ) においても、"量子" と "古典" の意味を 人為的に定義しているだけにすぎず、実在的という意味での 古典力学は 否定されていないことになる。
(Fig.20) 反時計方向の電流 = スピンアップ ? 時計方向 = スピンダウン ? ← 量子ビット ?

ここからは、D-Wave の量子コンピューターの 元の この論文 (= Nature ) と この論文 について説明する。
現在の理論によれば、例えば、ループ状の電流回路を貫く磁束が 1/2Φ0 のとき、2つの異なる重ね合わせ状態 (= 1 × Φ0 と 0 × Φ0 ) が 同時に存在するとしている。
これらは 2つの種類の 反時計、時計回りの電流を含んでおり、彼らはこの状態を それぞれ スピン-アップ、スピン-ダウンであると名付けてしまった。
もちろん、本当の スピンは 何も関係がないのにである。そして それらを 量子ビットとして利用しようとした。
(Fig.21) 量子トンネル もしくは 古典的な "熱的" 効果?

2種類の 外部の磁束を調節することによって、ポテンシャル障壁の高さや 井戸部の深さを 変化させる。
アニーリング (= トンネル効果 ) を 2つの基底状態の間の障壁を 徐々に 上げていく過程において 試行した。
古典的な 熱的振動によるアニーリングでは、ある時間に ポテンシャル障壁が ボルツマン因子である kBT よりも高くなった時点で、その障壁を超えることができず トンネル効果が ストップするとしている。
(Fig.22) 障壁が時間と伴に上昇。 → いつ (= tfreeze ) トンネル現象がストップする?

量子アニーリングにおいても、2つの状態間のトンネル現象は 障壁が十分に高くなった時間 (= tfreeze ) に ストップすることになる。
つまり このストップする時間 tfreeze よりも前に 右側の井戸部のポテンシャルが 左側の井戸よりも 低くなれば、粒子が 右側の井戸部に流れて、そっちの存在確率が上昇することになる ( Fig.21 )。
しかし 右側の井戸部が 時間 tfreeze (= 障壁が十分に高くなった時 ) よりも後に低くなったとしても、このトンネル現象 ( 熱的振動も含めた ) は 起きることが できずに 左右の井戸部の存在確率は 同じままということになる。
(Fig.23) 古典的な "熱的" 振動ラインは 正確なのか ?

古典的な熱的振動が このトンネル効果を引き起こす主要な要因だとすれば、トンネルがストップする時間 tfreeze は ボルツマン因子に従って 量子効果よりも 速くなるとしている。
障壁は時間と伴に上昇していくため、 より低い温度では、この障壁を乗り越えられるエネルギーが少ないため、より 早い時間に トンネルがストップするため、tfreeze の値は 小さくなる という具合にである。
実験結果では このストップ時間 tfreeze は 古典的 (= 熱的 ) に予測されるものよりもかすかに遅くなったとしている (= つまり量子効果? )。
問題は この古典力学的に予測されるラインというものが 本当に正確なのかということである。
(Fig.24) ↓ この結果は 本当に "量子"トンネル効果を表しているのか?

ボルツマン因子は もともと このページにあるように 自由粒子に基づいたものである。
一方で、超伝導体内部の電流は 常に強力な電磁気作用が働いているため、到底 自由な状態とは呼べない。
もちろん、このボルツマン因子による予測というのも 非常に大雑把なものである。
また 非常に極低温 ( 20 ~ 60 mK ) 状態においても このボルツマン因子が 電流に 精密にリンクしているという保証は まったくない。
さらに、量子 と 予測される古典力学との差は わずか tfreeze において
8 μs にすぎない。
この因子に依存した非常に粗い推定を考慮すれば、この古典的とされる予測ラインの信頼性は 非常に疑わしいと言わざるを得ない。
(Fig.25) クーロン + ドブロイ効果を 考慮する必要がある。

Fig.19 で述べたように、ジョセフソン電流の正弦曲線は 通常の電磁気作用では 起こり得ず、ドブロイの関係式が 必須であるにも関わらず、彼らは ポテンシャル計算において、その効果を 無視して、クーロン相互作用 (= I × V ) のみを用いた。
つまり 真のポテンシャル曲線を知るには、ドブロイ波などの 他の効果を 付け加えなければならない。
要するに ジョセフソンエネルギーの値そのものを 再考する必要があるということである。
(Fig.26) 障壁と2つの井戸型電位 = クーロン以外の効果。

そもそも、電磁気相互作用のみが関係しているとしたら、2つの井戸型曲線 ( と障壁 ) 自体が Fig.26 に示したように 形成されることはない。
結果的に、量子トンネル効果自体が 起こり得ない。
量子トンネル自体の信ぴょう性を問うには どうして磁束量子の整数倍が生じて、それがジョセフソン電流に影響を与えるのかという 根本的な理由を 解明しなければならない。
(Fig.27) D-Wave における 8つの量子ビット間のもつれ?

D-Wave の量子コンピューター自体は 量子もつれに依存していないと言われているが 最近の論文では、D-Wave のマシーンにおいても 量子もつれ効果が 観測できたとしている。
しかし 観測できたと言っても たったの8つの量子ビット間のもつれのみで、まったく実用化には程遠い。
また 各量子ビットは 結合伝導回路で繋がっているだけで、 単に通常の電磁気相互作用で リンクしているだけと考えるのが自然である。
実際に 装置内の 非常に短い距離 ( ~μm ) 内で、超光速 (= 非局所性 ) の もつれを証明することは 不可能である。
(Fig.28) 量子コンピューターはまったく非実用的。

基本的に 磁束量子ビットの コヒーレント ( 機能する ) 時間というのは 非常に 短く、 約 100 ナノ秒 ほどで壊れてしまう。 このサイト や このサイト (p.17) 参照のこと )。
こんなに短い時間内で、それらを使いこなし、その信頼性を確かめること自体不可能である。
さらに、この装置を正確に作動するには ほぼ絶対零度 (= 12.5 mK ) の温度が必須になってくる。
すでに 無数ともいえる学術論文が パブリッシュされている現在においても、 量子コンピューターが これほど非実用的であることを見れば、私達は そろそろ 根本的な考えを 改め、量子コンピューター ( と量子もつれ ) の概念自体を 諦める時期に来ていると言える。
(Ap.1) フォノン は 単なる 仮想の "準粒子" である。

超伝導体では、電子対 (= クーパー対 ) が 格子間隔よりもはるかに長い 数百ナノメーターの距離を挟んで形成されるとしている ( このサイト参照のこと )。
ご存じのとおり、2つの負の電子は 通常 互いに 反発しあう。
2つの電子間の 不自然な引力は 非常に曖昧な 準粒子 "フォノン" によって生じるとされている。
しかし このフォノンは 所詮は 仮想の準粒子にすぎず、科学者達は このフォノンの具体的な正体を 一刻も早く示すべきなのだが、ここで "真理の解明" が ストップしているのが現状である。
困ったものである。
(Ap.2) 量子化されたドブロイ波長。

マイスナー効果のために、超伝導体内部の磁場は 電子の運動 (= ローレンツ力による ) によって打ち消される。
しかし 超伝導体に空いた穴の内部では 磁束量子の整数倍の磁束 ( Φ = n × Φ0 ) が見られる。
(Ap.3)

このページに示したように、現在の量子力学では、この現象は ベクトルポテンシャル "A" の量子化によって起きるとされている。 Ap.3 の "2e" が "クーパー対" というわけである。
しかし 量子論は 現象を抽象化することだけで終わってしまい、肝心な この量子化されたベクトルポテンシャルの正体、メカニズムそのもの に関しては 頑として だんまりを押し通すのみである。
またもや、この時点で ”真理の追求”が止まっていることになる。
(Ap.4) ローレンツ力 + ドブロイの関係式。

各電子が ローレンツ力 ( F = evB ) に従って運動しており、かつ その軌道長が ドブロイ波長の 整数倍 と仮定すると、量子化された磁束を 自然に説明できる。
Ap.4 左は 遠心力が ローレンツ磁気力と釣り合っている式である。
Ap.4 右は 軌道の円周で ドブロイ波長の整数倍が成り立っているという意味である。
(Ap.5) ← Ap.4

Ap.4 を解くと、 Ap.5 が得られる。
また 全磁束 (= Φ ) は 磁束密度 (= B ) × この円軌道の面積 (= πr2 ) で与えられる。
結果、Ap.6 にあるように 全磁束 (= πr2B ) は 磁束密度 (= h/2e ) の 整数倍 に等しくなる。
(Ap.6) ドブロイ波による 磁束の量子化 (= h/2e )。

Ap.6 にあるように、穴を通過する 磁束 (= Φ ) は 量子化 ( Φ = n × Φ0 ) される。
これが クーパー対に 頼らない 磁束量子の起源である。
つまり、ポテンシャル障壁などの計算のときには、通常のクーロン力だけでなく このドブロイ波 ( の干渉作用 ) による力 (= ポテンシャル ) も考慮する必要がある。

2014/6/25 updated This site is link free.