
トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは存在しない。
1重項、3重項は "スピン" を意味しない。
(Fig.1) たくさんの非実在の準粒子 = 物性物理学。

多くの教科書では 量子力学は 最新のテクノロジーを説明できる 最も成功した理論だと 事あるごとに述べている。
しかし 21世紀となった今、実は これら量子力学は 古代の古文書と化して むしろ 科学の発展を妨げている 最大の障害物になっているのである。
これらの分野の研究者達は 単に 架空の粒子のみを 追い続け、 多くの貴重な時間を 無駄に費やしている。
Fig.1 に示したように、現在の物性物理学は 多くの 架空の準粒子に依存している。
研究者達は 人為的な "数学上" のモデルをこしらえて それを実験結果に近づけるよう
便利な準粒子を生みだし続けているにすぎない。
これらは 単に トリックにすぎず、何の実態も伴っていないことを このページに示す。
正確には BCS 理論の ボゴリューボフ粒子 (= γ ) は フェルミ粒子の準粒子である。
そして "フォノン" は "ボソン" の準粒子である。もちろん 両方とも 非実在の粒子であることは言うまでもない。
驚くことに、現在の量子力学には 非常に多くの 架空の粒子が存在しているのである。 ( Wiki を参照のこと。 ) 非常に 悲惨な状態である。
(Fig.2) "スピン" と "電荷" が 分離する ??
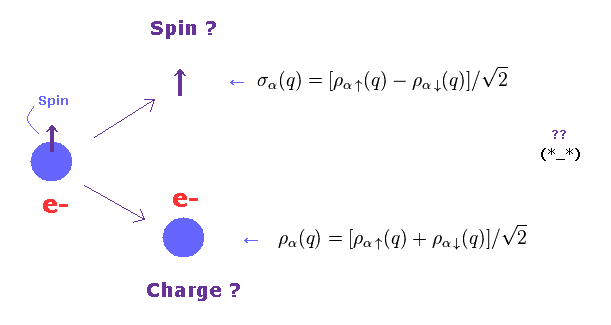
この非現実的な物性物理学では、何と 1つの粒子の "スピン" と "電荷" が 分離できてしまうと 彼らは主張している。
これらを "スピノン"、 "ホロン" と呼ぶ。
もちろん、 このサイトにあるように、これら準粒子は 実在の粒子ではない。
問題は、 科学者達は これら架空の準粒子達の 具体的な状態を 問うことを諦めてしまっていることである。
結果的に Fig.2 のような 非常に抽象的な 数式記号のみが 最新の量子力学という名の下に 残ってしまったのである。
さらに このサイトでは 何と 電子を "スピン"、"電荷"、"軌道" (= orbiton ) の3つの成分に 分解することに成功したと主張しているのである。
見てのとおり、現在の物性物理学は 現実の物理とは 大きくかけ離れて 単に ファンタジーのみを追いかける産物と化している。
(Fig.3) "スピン" なしの フェルミ粒子 !? 本当に ?
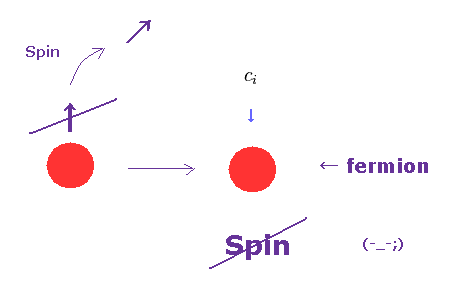
驚くことに、現在の物性物理学は スピンなしのフェルミ粒子に依存しているのである。 ( このサイト p.19 もしくは このサイトを参照のこと。 )
ご存じの通り、フェルミ粒子は 必ず スピン 1/2 を持つ。
つまり 現在の量子力学には スピンレスのフェルミ粒子というものは 存在しないはずである。
要するに これらの理論は 明らかに 自己矛盾しているのである。
もちろん、このページで説明するが、これらのスピンレスのフェルミ粒子は 単に 数学上 ( 物理でなく ) の記号にすぎず、何の実態も 伴っていない。
問題は 彼らは これらのスピンなしフェルミ粒子が 一体全体何なのかを 決して 調べようとしないのである。
つまり この 問うことを諦めてしまった状況では、 これら架空の準粒子のところで 科学 ( 物性物理学も含む ) がストップしてしまっているのである。
(Fig.4) フォノンと電子の 相互作用 !?

高温超伝導も含めた 現在の超伝導体は 基本的に 準粒子のフォノン と クーパー対 に依存している。
しかし Fig.4 を見て分かる通り、これらのフォノンと それらの相互作用は 単なる 数学上の 演算子にすぎない。
ここには 何の 具体的な 物理的イメージが 存在しないのである。
周りを見渡せば、現実の粒子達が 単なる数式記号で ない ことは 一目瞭然である。
(Fig.5) フォノン機構は ドブロイ波の整数倍 で説明可能。
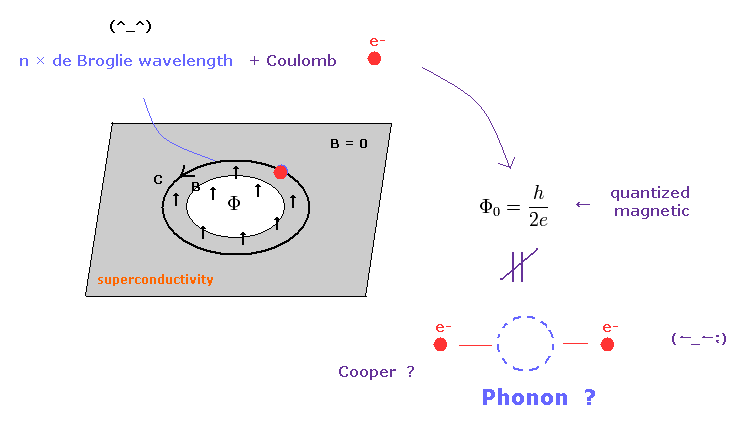
フォノンと クーパー対 が信じられている 実験的な要因は すばり 磁束量子 (= Φ = h/2e ) にあると言っていい。
( 様々なところをチェックした限り これが クーパー対の 唯一の直接的な実験事実 である。 )
このページに示したように、このフォノンに依存したクーパー対は ベクトルポテンシャル A を使用している。
実は このクーパー対も ”位相” という形で ドブロイ波の整数倍という条件を使用しているのである。 .
( 彼らは この "位相"なるものの正体を すみやかに解明すべきである。 )
このページでは、この磁束量子を 実在のドブロイ波と 古典的なクーロン力で 説明することができた。
このドブロイ理論と フォノン機構の 決定的な相違は
まさに "リアリティー" である。
この磁束量子に フォノンという概念は 必要ない。なぜなら フォノンは 非実在の仮想の粒子だからである
(Fig.6) "虚数" 時間 は リアルなのか?

実は、フォノンが関与する すべての機構は 非現実的な 虚時間 ( t = -iτ ) に依存している。
伝播関数 (= グリーン関数 ) は ある状態の 時間変化を計算するのに使われる。
もちろん、現実のものは 実時間 ( 虚数でなく ) に伴って変化することは言うまでもない。
つまり 現在の物性物理学は 完全に 現実離れしていると言える。
(Fig.7) "虚時間" は ボルツマン因子を 組み込みのに必須である。

有限温度では、 ボルツマン因子 は そのエネルギー (= H ) に関して 状態の 確率密度を表す。
このボルツマン因子 (= 青線 ) を伝播関数に組み込むには 実時間を虚時間に変える必要がある。
この 人為的な手法は 飛び飛びの 虚時間用の振動数を得るためのものである。
ボルツマン因子に基づく 飛び飛びの振動数は 実時間の 連続した振動数と 完全に 異なるものである。
量子色力学 も この虚時間に依存しており、これらの概念は 現実のものとは 到底言えない代物である。
(Fig.8) コンピューターなしの物性物理学は "無意味な"数式記号の集まり。

量子力学が生まれた 1920 年代は もちろん コンピューターなどはなかった。
つまり 当時の研究者達は 3体問題であるヘリウムを計算することが できなかった。
もちろん、3体問題ですら計算できないとすると、ほぼ無数の原子を含む 物性物理学を 取り扱うことは 到底 不可能である。
しかし これらの深刻な状況でも、研究者達は 良い職を求めて 研究をして 論文を書き続けなければならない。
そういった状況の中で 非実在的な準粒子が たくさん作りだされ 数学上の道具として 使用されるようになった。
高エネルギー領域では 何と 10 次元 という どう考えてもあり得ない 超弦理論のみが 唯一の統一理論として 残ってしまった。非劇としか言いようがない。
これら 架空の理論は 1920 年から 1990 年代の時間の空白期間を 埋めるのに 必要不可欠だったのである。
(Fig.9) 物性物理学 = 数学の "象形文字" で 溢れた 古典。

約 1980 年頃、 アップル II という 最初の オールインワンのパソコンが開発された。
しかし、初期モデルのため より複雑な 分子間相互作用を扱うには もっと高性能のコンピューターがでる 1990 年代 まで 待つ必要があった。
すでに述べたように、この 非常に長い ( 1920 - 1990 年 ) 時間の ギャップが 多くの 非現実的な理論を 生み出す源になった。
問題は 1990 年代に 高性能のコンピューターが出現した後でさえ、従来の 数学上の ( 物理でなく ) 準粒子に 完全に依存した 古い理論が まるで 古代の呪文のように 生き続けてしまったことである。
何らかの教科書を眺めれば 一目で これらの古〜い手法が 現在の 21 世紀に 相応しくないものであることは 分かるだろう。
なぜなら 準粒子、仮想粒子というのは 最初から 非実在のものだからである。
(Fig.10) "架空" の理論は どう形成され、世に広まるのか?
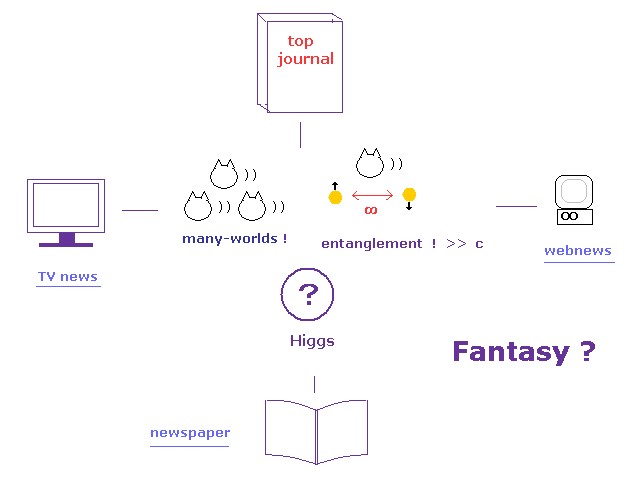
量子力学には 何の 現実性もない。
それは 超光速の エンタングルメントや 多世界 (= 重ね合わせ ) などの 現実離れした概念に依存している。
しかし 1920 年代の コンピューターなしの状況では 他の理論は 残ることができなかった。
そのため 21 世紀になった今でさえ、様々な ( トップ ) ジャーナルでさえ、これら
架空の現象を取り扱っている。
これらの理論は 本質的に 非現実の概念であるため、実質的な 進展がないものが多い。 ( お騒がせの "量子コンピューター" がいい例である。 ).
それに拍車をかけるように テレビ、ウェブ、新聞などの 様々な マスメディアが 大々的に ファンタジーと化した理論を 報道して 助長してしまった。
つまり 公共の電波を用いて 一般人 果ては 新しい学生達の 夢や その後の人生を 狂わせてしまっているという 恐ろしい構図になっている。
記憶に新しいのが ヒッグス粒子発見の 派手なニュースである。
あれだけ 無数のマスメディアが このニュースを 大々的に 繰り返し報道したのにも関わらず、一般人で それらニュースで 質量獲得のメカニズムを よく理解できた方は あまりいらっしゃらないと思われる。
理由は簡単で 本来、現実性のない 抽象的な 対称性などの数式記号の世界を あたかも 現実の物体 (= ヒッグスの海とか ) を使って表現しようとしていたため 余りにも無理がありすぎて 継ぎはぎだらけの説明になってしまったからである。
最初から、"単なる数式記号の話として諦めてください。" と 一言前置きすれば 一発で納得してもらえるのに 見てて苦しくて仕方がない。
(Fig.11) マクロの効果、しかも 実験値そのものでなく その "比" しか扱えない。
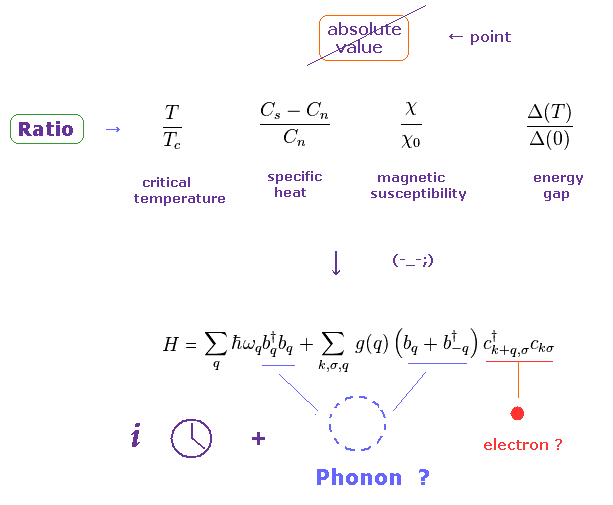
非現実的な スピン や 波動関数のために、現在の物性物理学は 実は 電子 や 原子核などの 具体的な ミクロの世界に 入っていけないのである。
それらが 扱えるのは 単に 臨界温度、比熱、磁化率、エネルギーギャップなどの
巨視的な効果のみである。
さらに 現在の スピン模型は 抽象的すぎるため これらの値の絶対値そのものを 予測することができない ( 要するに 単なる "比" だけ )。
実験値の "比" ( 絶対値でなく ) に合わせるために、様々な 架空の準粒子を 人為的に こしらえて 利用しているだけである。
これらの 架空のモデル形式に依存している限り 物性分野で 実際の粒子間相互作用の
ミクロの実世界に 入っていくことは 永久に 不可能である。
(Fig.12) 中性子散乱 = スピン波 もしくは フォノン ?

フォノン や スピン波の 非現実的な現象の 直接的な実験事実は 中性子 ( もしくは 光 ) 散乱などだけである。
彼らは これら フォノンや スピン波を 直接見ているわけではない。
単に 散乱された中性子のエネルギー変化などから それらの存在を 推定しているだけにすぎない。
( 例えば、 エネルギー遷移 中性子 → フォノン、 フォノン → 中性子 など )。
そもそも フォノン自体 実際には実在しない準粒子にすぎないのに。
(Fig.13) "原子振動" の候補として "フォノン" 以外 選択肢がない !?
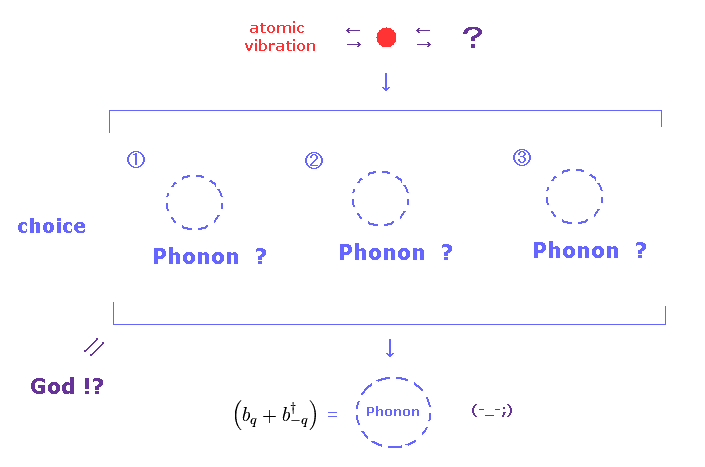
中性子は 主に 原子核 と 磁気モーメントの 2大要因によって散乱される。
原子核による散乱機構は 原子核内部の 力が絡むため、非常に複雑である。
この中性子散乱は 原子核 (= 原子 ) の振動の 一種のセンサーとなり得る。
しかし 現在の 数学上の量子力学は 例え コンピューターを使用したとしても
難解すぎて 多体効果を 正確に 予測できない。
( なぜなら 量子力学とは 本来 コンピューターの使用を想定していない 独自の理論だからである。 )
それは 非常に抽象的な 数式記号に頼らざるを得ない。
このことが 原子振動として 非実在の準粒子 (= フォノン ) に頼らざるを得なくなった理由である。
(Fig.14) 磁気モーメントの候補として "スピン" 以外の選択肢がない !?

中性子が散乱される 2大要因の1つが 磁気モーメントである。
磁気モーメントは 非常に弱いが 電子軌道が 原子核と比して 非常に広範囲に広がっているため、この効果は 原子核散乱ほどの大きさになる。
重要な点は 現在の物性物理学は 磁気モーメントの起源として "スピン" しか 考慮に入れていないという点である。
そのため 何らかの磁気モーメントのゆらぎを観測したとき、この ゆらぎは "スピン" からのものだと すぐさま 決めつけてしまう。
彼らは 大きく バライティーに富む 磁気モーメントを有する 軌道運動などの効果を 軽視する傾向にある。
このページに示したように、これら スピンゆらぎ理論は 数学上のトリックで溢れており、 明白な物理的イメージが まったくない。
(Fig.15) 2つのフェルミ粒子が 4つのフェルミ粒子と等しい?
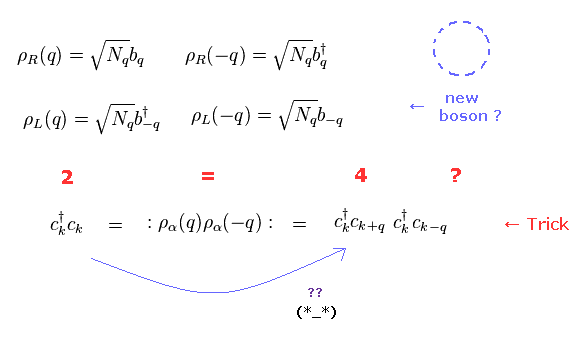
スピンパイエルス転移と スピノン、ホロンの分離のためには、Fig.15 のような人為的な数学上のトリックに頼らざるを得ない。
驚くことに Fig.15 では、 2つのフェルミ粒子 (= c†c ) が 4つの フェルミ粒子 (= c†cc†c ) に等しいとしているのである。
つまり " 2 = 4 " という 奇妙な等式が成り立っていると 彼らは主張しているのである。
どうして このような奇妙な状況がおきたのだろうか?
( このサイトなど参照。 )
また ここからは 何の 物理的イメージが 存在しないことを 予め断っておく。
最先端とされる 物性物理学でさえ、単に 抽象的な 数式記号のみで 物理的実体が ないということである。
(Eq.1)

Eq.1 では、 c† と c は 電子の生成消滅演算子である。
"k" と "p" は それぞれ 波数 と 運動量 である ( ここで ħ は 省いているため、 k = p )。
ε は エネルギーである。
(Eq.2)

これらの 電子の演算子は Eq.2 の反交換関係を満たす。
この関係が パウリの排他原理の起源だと 彼らは主張している。
しかし 一目見て分かるとおり、これらは 単に 数学記号間のルールにすぎない。
もっと 具体的なメカニズムを問おうとすると " Shut up ! " ということになる。
(Eq.3)
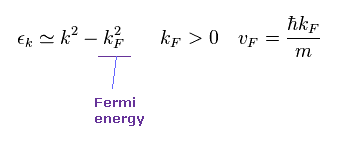
kF と vF は フェルミエネルギーと フェルミ速度である。
この フェルミエネルギー (= EF ) は 物性物理学の分野で しばしば登場する 最も重要な概念である。
しかし、ここには 明白な 物理的イメージが存在しない。
(Fig.16) フェルミエネルギーは 非常に曖昧な概念である。
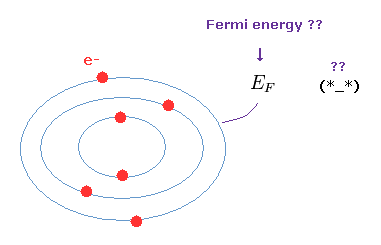
軌道は 低いエネルギー準位から順に埋まっていく。
各軌道は パウリの排他原理のために 2つの電子までしか含めない。
最も外側の高いエネルギーレベルを "フェルミレベル ( エネルギー )" という。
フェルミレベルの これらの電子は 他の電子で すでに埋まった 内殻の軌道に
入ることができない。
(Eq.4) 近似的な表現。

ここで Eq.4 のように定義する。
エネルギー εk は 波数 "k" の二乗である。
つまり 1つのエネルギー ε には 2つの 波数 (= ± k ) が存在する。
Eq.4 の上の式 (= R+ ) では、この "k" は +kF に近いときを表し、 Eq.4 下の式 (= L- ) では この "k" は -kF に近いときを表す。
ここでは ± の符号を R = + や L = - という対応形式でも表すことにする。
(Eq.5) 密度 ρ の定義。

ここで 彼らは 密度演算子 ρ を Eq.5 のように定義した。
エネルギーが フェルミエネルギーに近いとき、 ρ+ = ρR の中に含まれる "k" は +kF に近くなる。
( 一方で、 ρ- = ρL 内の "k" は -kF に近くなる。 )
(Eq.6) 奇妙な交換関係。

Eq.5 を見て分かるとおり、 この密度 ρ は 2つのフェルミ粒子で構成されているため これは ボソンのように振舞う。
問題は 運動量 "q" が "-q" と異なるときでさえ、 これら ρ 演算子の交換子はゼロにならない。なぜなのだろうか?
非常に奇妙である。
(Eq.7)

Eq.6 では、 Nq を Eq.7 のように定義した。
"q" が 運動量で、 "2π/L" が 波数の単位である。
Eq.5 を Eq.6 に代入して、 Eq.2 の反交換関係を用いると、 Eq.8 を得る。
(Eq.8)

Eq.8 では、 "n" (= c†c ) は 数演算子である。
ここで突然、数演算子を 単なる "数" (= Nq ) に変えてしまった。これは 明らかに トリックである。
重要なポイントは ここで 最も低い波数 としてk0 を定義したことである。
これは あらゆる波数 (= 運動量 ) を含む 通常の相対論的な場の量子論と 明らかに異なる。
結果的に nk-q は k0-q と k0 間に 余分の 波数 を含むことになり、この差が Nq を与えるというからくりである。
しかし この方法は 上限の 波数を 指定していないのである。
下限だけしてしているのは これもまた トリックと思われても仕方がない。
(Eq.9)

ここで ハミルトニアン (= Eq.1 ) と ρ (= Eq.5 ) の交換関係を考える。
"c" の反交換の性質のために、 c が 隣りに移動すると、マイナスの符号がつく。
c が 2つ分の演算子移動したときは、符号は変わらない。
(Eq.10)

Eq.9 から、 Eq.10 を得る。
Eq.4 や ε = vFk = vFq を用いた。
(Eq.11)
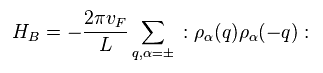
ここで Eq.11 のような 新しいハミルトニアンを定義する。
どうして このハミルトニアンを採用したのかという 妥当な理由は 何もない。
(Eq.12)

もちろん、これは 完全に 人為的な定義である。
2つのフェルミ粒子 (= cc ) が 1つのボソン (= b ) を形成する。そのため Eq.13 のような 新たなボソン (= b ) を定義した。
(Eq.13)

つまり 単に数学上のツールとして 新たな非実在のボソンを 導入したにすぎない。
これが 現在の物性物理学の実態である。
Eq.11 の新しいハミルトニアンと Eq.6 の関係式を用いて、HB と ρ の交換子は
(Eq.14)

Eq.14 の結果は Eq.10 に ちょうど等しい。それらのハミルトニアン (= H0 と HB ) は 完全に 異なる形にも関わらずだ。
しかし ここで突然 次の 間違った 新たな関係式 ( 2 = 4 !? ) を採用してしまう。
(Eq.15) 間違った式。

2つの 異なる ハミルトニアン と ρ の交換子は 同じ結果を与える。そのため これらの異なったハミルトニアンを 同じものとして扱ってしまえ という仮定である。
Eq.15 を見て分かるとおり、 H0 は 単に 2つの演算子 (= c†c ) のみを含む。
一方で、 HB は 4つの演算子 (= c†cc†c ) を含む。
つまり H0 = HB の式は 完全に 間違いである。( 片方は 演算子を単なる数に変えてしまった + 人為的な定義 )
しかし この間違った式が 非実在の準粒子、スピノン、ホロン や スピンパイエルス転移などの説明に
必要なのである。
(Eq.16) 間違った関係式の採用。

Eq.15 の間違った式を用いて、準粒子 スピノン と ホロン を導きだす。
一目見て、Eq.16 の式が 理不尽なことが分かる。
H0 の単位は 密度 1つ分 で、 一方 HB のほうは 密度 × 密度 の単位構成になっている。
両者は まったく異なるものだが、ここで この 密度 × 密度の形を 等しいものとして選ぶ。
( Eq.16 では、負の符号を省略した。 )
(Eq.17)

Eq.16 では、 σ は "up" もしくは "down" のスピンを意味する。
(Eq.18) 1つの粒子の スピン と 電荷 への分離 ?
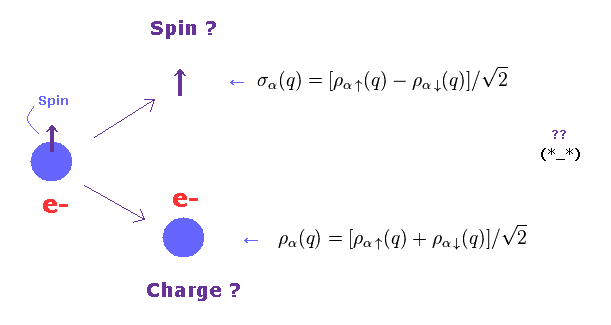
Eq.18 では、 "up" と "down" スピンの粒子の和が 全電荷 (= ρα ) を表す。
そして "up" と "down" スピン粒子の差が スピン磁気モーメント (= σα ) を表す。
(Eq.19)

Eq.18 を Eq.19 に代入して、 Eq.16 の ハミルトニアン (= HB ) を得る。
よって Eq.19 の式は 粒子が スピン (= スピノン ) と 電荷 (= ホロン ) に分離された状態だと 主張しているのである。
しかし 見て分かるとおり、これらは単なる抽象的な演算子にすぎず、物理的な
性質は 何もない。
もちろん、現実の素粒子を "スピン" と "電荷" に分離することは
不可能である。
このサイトにあるように、単に 光電子スペクトルを観測したにすぎない。
これらの結果を 人為的な定義と組み合わせることによって、スピンと電荷が分離したと 主張しているだけにすぎない。
これが 最新の物性物理学の実態である。
( 一般の方は もっと最先端のイメージを持たれていたかも知れないが まったく異なるものなのである。 )
(Eq.20)

ここで Eq.13 の新たなボソンを用いて θ を Eq.20 のように定義する。
またもや Eq.21 のように 新たな ボソン (= Φ ) を導入する。
(Eq.21) 新ボソン ?

Eq.13、Eq.20、Eq.21 を用いると これら Φ と Π が 通常の Eq.22 の 交換関係を満足することが分かる。
だから これも ボソンだというわけである。
(Eq.22) 交換子 = 新たなボソン ?

ここで 次を使う。
(Eq.23)

Eq.11 のハミルトニアン (= HB ) が Eq.21 を用いて、 Eq.24 のように表せることが分かる。
(Eq.24) 新たなボソンによるハミルトニアン ?

このように 現在の物性物理学は 数学上のテクニックとして 新たな非実在ボソンを生成させて利用しようとしているだけなのである。
もっと 現実に則した物理をやらなければならない。
(Eq.25)
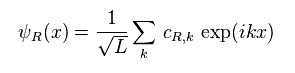
フェルミ粒子 ψ を Eq.25 のように定義した。
見てわかるとおり、現在の量子論には 多くの人為的な定義が存在する。
b ( Eq.13 と Eq.5 を参照 ) と ψ (= Eq.25) の交換子は
(Eq.26)

ここで 次を定義する。
(Eq.27)

Eq.26 の赤線は Eq.2 の反交換関係である。
結果、次の交換関係得る。
(Eq.28)
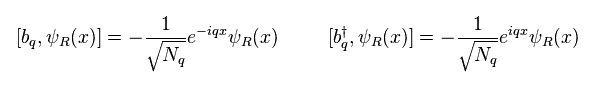
(Eq.29) コヒーレント状態。

b と b† が ボソンで 交換関係を満たすとき、Eq.29 の式が成り立つ。
ここで Eq.30 の公式を用いた。
(Eq.30)

ここで Eq.28 と Eq.29 を比較して、それらの 赤、青の部分 ( Eq.31 ) が 互いにちょうど等しいと判断してしまう。
そして それらを組みかえて新たな式を合成する。
これは あまりにも 強引な解釈である。
(Eq.31)

残念ながら、この等式は 無理があって 正しくない。
最終的に Eq.29 の両方の部分を用いて、次の定義ができる。
(Eq.32)

ここで θR は Eq.20 である。
もちろん、 Eq.32 ( もしくは Eq.31 ) の式は 間違いである。
なぜなら
(Eq.33)

ボソンは いくら集まっても フェルミ粒子には なれないからである。
つまり 現在の物性物理学は 数学的にも 物理的にも 完全に 間違った仮定に依存している。
まさに 数学上のトリックと言える。
(Eq.34)

同様にして Eq.34 を得る。
Eq.32、 Eq.34、 Eq.21 から 次を得る。
(Eq.35)

結果、
(Eq.36)

ここで 次を使った。
(Eq.37)

(Fig.16) "スピンパイエルス" 転移は 本当に "スピン" を意味するのか?
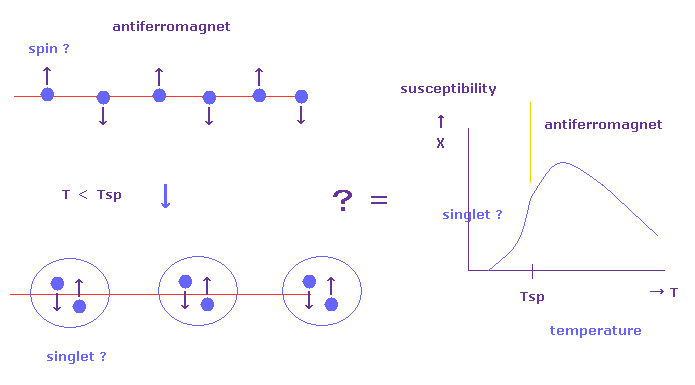
スピンパイエルス転移では CuGeO3 などの 反磁性体が ある臨界温度 (= Tsp ) 以下で 非磁性の 1重項 (= ダイマー化 ) になることによって生じるとされている。
もちろん、現実離れした スピンを 直接見ることはできない。
彼らは これらの状態を Fig.16 の 磁化率 (= χ ) の変化などから 推定しているにすぎない。
反磁性体では、外磁場に反応する 磁化率 ( 帯磁率 ) は 1重項のときよるも はるかに大きいとしている。
1重項状態では "up" と "down" の 2つのスピンの原子が 互いに固く結合しているとしている。( もちろん、これらの状態を 直接 見ることはできない。 )
また 彼らは これらスピン間に働く 強力な結合力について 詳細を 決して 語ろうとしない。
このページに示したように、 (反) 磁性体のスピン間の相互作用エネルギーは スピン・スピン磁気モーメント相互作用を用いて 表せないほど 強いものである。
(Fig.17) スピンレスのフェルミ粒子は 必要 ?

驚くことに、スピン・パイエルス転移には スピンがないフェルミ粒子が必要になるらしい。
( このサイト や このサイトを参照のこと。 )
非現実的な 超対称性粒子にさえ、スピンなしのフェルミ粒子などは 存在しないのにである。
つまり、最初から これらの理論は 矛盾を抱えていることになる。
(Eq.38) スピンなし フェルミ粒子の 非局所的な重ね合わせ !?

彼らは スピン演算子 S+ と S- を Eq.38 のように定義した。
Eq.38 では、 ci は 原子位置 "i" における スピンなしのフェルミ粒子である。
残念ながら、これらのスピンモデルは 数学的な制限により、 1次元のスピン系しか 扱えない。
単純な 1次元系においても 何らかの 近似に頼らざるを得ない。
驚くことに、これらスピン演算子は 多くの他の場所のスピンを含んでいるのである。
1 から i -1 までの 異なった位置の 原子スピンが "i" の原子に影響を与える (= 非局所性 )。
残念ながら これら 非局所性のスピンレスフェルミ粒子を 現実の物で説明することはできない。
(Eq.39)
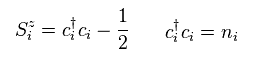
彼らは Sz 成分を Eq.39 のように定義した。
Eq.38 と Eq.39 を見て分かるように、 これらフェルミ粒子 (= c ) には 何の スピンもない。そのため 異なったスピン成分内でも 共通の演算子として 使用できるわけである。
もちろん、ここには 何の具体的な根拠は 存在しない。
(Eq.40)
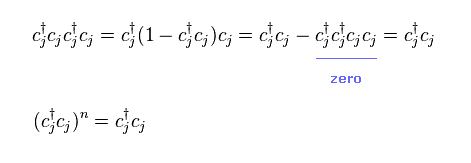
フェルミ粒子は Eq.2 の 反交換関係に従う。
つまり 2つの隣り合った同じ演算子 "cc" や "c†c†" は "ゼロ" になる。
結果、
(Eq.41)

Eq.41 を用いて、 Eq.38 は、
(Eq.42)

Sx と Sy のスピン成分は Eq.43 のように表せる。
この変換は "ヨルダン -ウィグナー変換 " と呼ばれる。
(Eq.43)
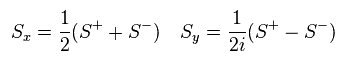
(Eq.44) XXZ 1次元 スピンモデル。

XY モデルは 単純なため 完全に解くことができる。
しかし XY モデルには z 成分のスピンがなく、本当の原子状態を 表せない。
XXZ ハイゼンベルグスピンモデルは スピンパイエルス転移の説明に 使われる。
問題は XXZ モデルは 解くことができないため、数値計算などの 粗い近似に頼るらざるを得ない。 .
(Eq.45)
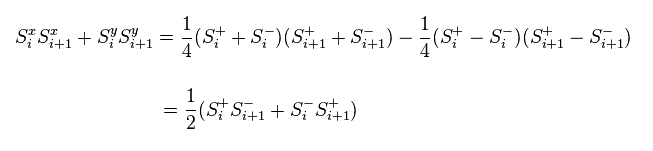
Eq.43 を Eq.44 に代入して、 Eq.45 ( x, y 部分 ) を得る。
また Eq.42 の定義と 反交換関係を用いて、次を得る。
(Eq.46)

また
(Eq.47)

Eq.39、 Eq.46、 Eq.47 を Eq.45 と Eq.44 に代入して 次を得る。
(Eq.48)

スピン・パイエルス転移では 原子間距離の一様性が壊れている。
そのため 次のハミルトニアンを採用しなければならない。
(Eq.49)

Eq.49 では、奇数原子間と 偶数原子間の距離 ( 相互作用 ) が 異なっている。
見てのとおり、彼らは 実験結果に合わせるように ハミルトニアンの形を
意図的に変化させているだけである。
つまり、これらのモデルは 自然の結果では まったくない。
(Eq.50)

(Eq.51)

ここで G= 2π × n で かつ
(Eq.52)

Eq.52 では、 Eq.15, Eq.24, Eq.36 のような 人為的な変換に頼る必要がある。
結果的に Eq.51 のハミルトニアンは 次のようになる。
(Eq.53)

ここで
(Eq.54)

Eq.20 を参照のこと。
また
(Eq.55)

これらの方法は "位相ハミルトニアン" と呼ばれる。
フェルミ波数を 次のように定義する。
(Eq.56)
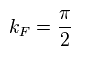
問題は これらの形は 他のスピン波理論と 一致しないということである。
そのため Eq.55 の係数を 次のように 人為的に変化させてしまう。
(Eq.57)

ここでは
(Eq.58)

これも 一種の 操作にすぎない。
ここで π/2 からの変化を考える。
(Eq.59)

Eq.53 のハミルトニアンを 変分関数として扱う。
(Eq.60)
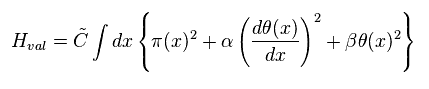
係数 α と β は 変分パラメーターである。
つまり これらは 自由に調整できる フリーパラメーターである。
θ と π の フーリエ変換は
(Eq.61)

Eq.61 を Eq.60 に代入し、かつ 突然 新たなボソン (= "a" と "b" ) を 人為的に導入する。
(Eq.62) 新たなボソン導入 ← また 数学上のトリック。

もちろん、これらのボソンは 非実在の 準粒子である。
しかし Eq.63 のように これら新ボソンに基づいた 新たな真空を定義してしまう。
(Eq.63)

Eq.63 の真空を Eq.60 のハミルトニアンに適用して、
(Eq.64)

エネルギーの結果は、
(Eq.65)
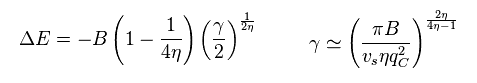
反磁性体では、 Δ ( Eq.44 参照 ) は 正 で、 η ( Eq.58 参照 ) は 次のようになる。
( これら Δ や η は フリーパラメーターである。 )
(Eq.66)

Eq.65 から、 B の指数は 次のようになる ( γ 内に含まれる B も考慮して )。
(Eq.67)

Eq.55 から B は δ (= 奇数、偶数サイトの結合定数の差 ) に比例している。
この スピン間の結合定数が ある 変数 λ や、 各原子位置の ゆがみ (= u ) に比例すると仮定すると、 Eq.65 のエネルギーは 次のように表せる。
(Eq.68)

ここで η = 1 とする (= この選択は 任意性があるため予測にならない。 )
(Eq.69)
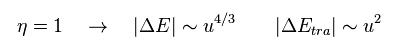
原子位置の各ゆがみ (= u ) が小さいとき、エネルギーの減少 (= "u" の 4/3 乗 ) は ゆがみエネルギーの上昇 (= "u" の2乗 ) よりも大きくなると 彼らは主張している。
しかし ゆがみと スピン間エネルギーの間をつなげる Eq.68 の λ の値 が 良く分かっていない。
また 今まで見て分かるとおり、これらの手法は 様々な人為的な定義や 準粒子に依存している。
要するに 自然な帰結とは 到底 言えるものではない。
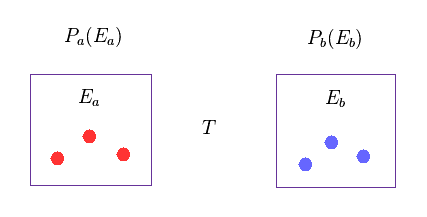
(Eq.70) ボルツマン因子は 古典力学。
多くの古典力学に基づく理論が 実際の現象に一致し、現在の物性物理学の
基礎 となっていることが知られている。
例えば、ボルツマン因子、ドルーデの伝導度、 Curie-Weiss の法則など。
ここで ボルツマン因子 (= exp(-βE) ) を 古典力学を用いて 導出する。
Eq.70 では、 Ea と Eb は A と B それぞれの 独立した系のエネルギーである。
これらの状態の 確率密度は それぞれ Pa と Pb である。
T は 温度である。
(Eq.71)

Eq.71 では、 E と P(E) は 全エネルギーと 確率密度である。
Eq.71 の P(E) を Ea で微分して 次を得る。
(Eq.72)
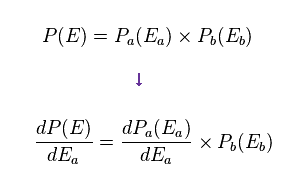
この微分を 次のようにも表せる。
(Eq.73)

Eq.72 は Eq.73 に等しい。
(Eq.74)

Eq.74 の両辺を Eq.71 の "P" で割ると 次を得る。
(Eq.75)

Eq.75 では、左辺は 変数 "E" のみ、右辺は Ea のみで 構成されている。
2つの独立した変数であることを考慮すると 両辺とも 何らかの定数 (= -β ) になる必要がある。
結果的に
(Eq.76)
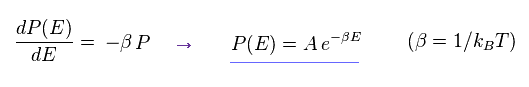
これが 有名な ボルツマン因子である。
要するに ボルツマン因子は 完全に 古典力学に基づく概念と言える。
(Eq.77)
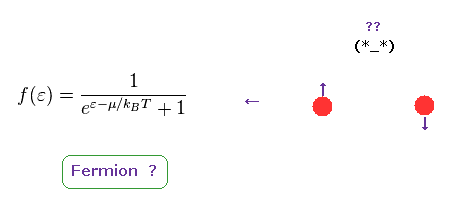
このページに示したように、フェルミ統計は Eq.77 のようになる。
Eq.77 では、 ε は エネルギーで、 μ は フェルミエネルギーである。
物性物理学の 様々な手法を見る限り、Eq.77 の フェルミ分布の式を そのまま 用いているものは
皆無である。
彼らは 必ず Eq.77 を 非常に 粗い近似に置き換えている。
つまり Eq.77 が 本当に正しいのかどうか まだ 証明されていない ということである。
(Eq.78)

ここで 非常に低温 ( T → 0 ) 状態を考える。
系の エネルギー (= ε ) が フェルミエネルギー (= μ ) より高いとき、
(Eq.79)

Eq.77 の確率分布 f(E) は T → 0 の極限で ゼロ になる。
また エネルギーが フェルミエネルギーより低いとき、
(Eq.80)

f(E) は T → 0 の極限で "1" になる。
そのため 彼らは フェルミ粒子は フェルミエネルギー準位の下を 埋めていると主張している。
しかし この近似は 粗すぎて Eq.77 が 本当に正しいのかどうか 判断できない。
(Eq.81)
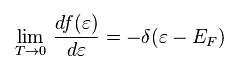
Eq.81 は ゾンマーフェルト展開である。
δ( ) は デルタ関数である。
またもや これは 非常に 粗い近似である。
(Eq.82)
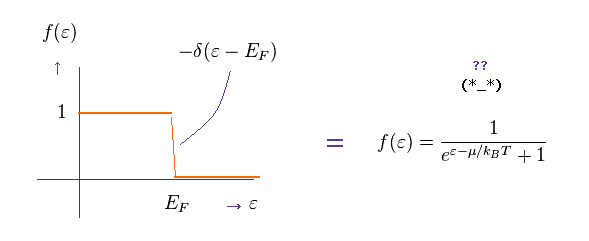
フェルミエネルギーの地点での Eq.80 (= 1 ) から Eq.79 (= 0 ) への 急激な変化を見ると、Eq.82 の デルタ関数が 理解できる。
( ε = EF で、このデルタ関数が 無限大になる。 )
一方で、プランク定数 (= ドブロイ波の量子化 ) は ボルツマン因子は 今までに 実験によって 正しいと実証されている。
(Eq.83) プランク定数と ボルツマン因子は 正しい。

(Eq.84)

"フォノン" は 現在の物性物理学で 最も重要な概念である。
このフォノンのハミルトニアンは Eq.84 のようになる。
Eq.84 の最後の項が フォノン (= b ) と 電子 (= c ) 間の相互作用を表していると 彼らは主張している。
見てのとおり、これらの相互作用は 抽象的すぎて 現在の複雑な現象に使用できない。
(Eq.85) 結合定数。

Eq.85 は フォノンと電子間の 結合定数である。
残念ながら、これらのパラメーターは 単に仮想のものである。
(Eq.86)

相互作用項 (= Eq.84 の最後の項 ) の意味は Eq.86 のようになる。
Eq.86 左では、 運動量 "k+q" の電子は エネルギー (= q ) を フォノン (= b ) に与えて、 "k" になる。
( "bq" は "q" のフォノンが 消滅したという意味。 )
Eq.86 右図の意味も Eq.86 左図と 同じである。
"b-q†" は 運動量 "-q" のフォノンが 生成された という意味だからである。
(Eq.87) 虚時間が必要。

実は 現在の物性物理学は フォノンの遷移に 仮想の"虚数時間" というものに頼っているのである。
つまり これらの理論は 最初から
リアリティーが ない と言っていい。
ここで この虚数時間 (= - i τ ) が フォノンのグリーン関数で どのように使用されているか述べる。
ハイゼンベルグ ( 相互作用 ) 描像の 通常の演算子の形は、
(Eq.88)

ここで 突然 実時間 (= t ) を 虚数時間 (= τ ) に変える。
(Eq.89)
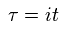
Eq.89 を Eq.88 に代入して 次を得る。
(Eq.90)

グリーン関数は 伝播関数で どのように状態が 時間とともに変化するかを表している。
この 温度グリーン関数では、 虚数時間の方向しか見ていない。
( 私たちは 実時間の変化が知りたいのにである。 )
(Eq.91)

Eq.91 では、 θ( τ - τ' ) は 階段関数である。
( τ - τ' > 0 のとき、 この θ は "1" になる。 τ - τ' < 0 のとき、 この θ は "0" になる。 )
2つの演算子は 時間順序に並んでいるとする (= Tr, 右が前、左が後。 )
(Eq.92)
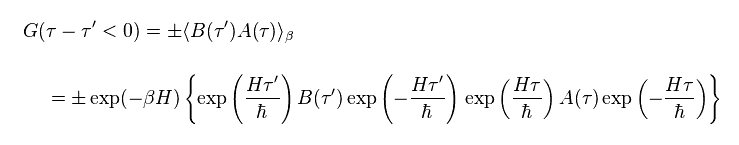
Eq.92 は Eq.91 の最後の項のみピックアップしている。
フェルミ粒子では、 交換は 負の符号 ( ± : + は ボソン、 - は フェルミ粒子 ) を与える。
有限温度では、確率密度は ボルツマン因子 (= exp(-βH) ) × グリーン関数で与えられる。
(Eq.93)

ハミルトニアン (= H ) の 両サイドの固有関数が 同じであるとする。
これを 行列表現で表せば、その行列の トレース和 になる。
そして これら行列の順序は Eq.93 のように 循環できる。
Eq.93 を用いると、 Eq.92 は、
(Eq.94)

Eq.94 では、H を含む指数関数同士は 交換可能である。
左側の 3つの演算子を 右に移した。
次に Eq.94 の左側から 2つの指数関数 (= exp(-βH) exp(βH) = "1" ) を付加する。
(Eq.95)

Eq.95 のように、 虚数時間 τ-τ' は ボルツマン因子を吸収後、 βħ + τ-τ' に変化する。
重要な点は 次の人為的な条件を適用する必要がある。
(Eq.96)

Eq.96 の条件のもとで、グリーン関数は 虚時間 βħ の間隔で 周期的になると 彼らは主張している。
しかし 私たちは 実時間の変化が知りたいのに、ここには 何の現実性もない。
(Eq.97)
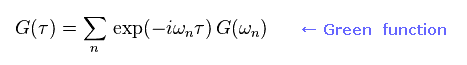
Eq.97 は グリーン関数の フーリエ変換である。
時間の周期性を考慮すると、これらの 振動数 (= ω ) は 次のように 飛び飛びの値になる。
(Eq.98) これは 単に数学上のトリックにすぎない。

フェルミ粒子のグリーン関数では、負の符号がつくため、これらの振動数は 奇数 × π になる。
ここには 何の 物理的イメージもない。
しかし これが 最新の物性物理学の実態なのである。

2014/1/18 updated This site is link free.