
トップページ (2電子原子も含む正確な新ボーア模型)
ボーアモデル vs. ベルの不等式 (CHSH-type)
光子対を用いた実験では、ベルの不等式が破れてたと言われている。
しかし、これらの実験では、光子の同時検出効率は低い (= ” detection loophole ”)
この欠陥 (loophole) を除くために、Be+ や Yb+ などの イオン対 を使った様々な実験が行われた。
一般的には、これらの実験は検出効率が高いにも関わらず、ベルの不等式を破るのに成功したと言われている。
しかし、重要な点は 両方とも”ベルの不等式の破れ”という共通の語句を使用しているが、イオントラップの実験は光子対の実験とは まったく異なる性質のものだということだ。
光子の場合は、互いに平行な偏光を持つ光子対を 偏光板を通過後に測定したとき、いわゆる”量子のもつれ”の現象を示す。
(しかし、このページで示したように、我々は 局所実在性の電磁波モデルを用いることによって、自然に ベルの不等式の破れの現象を説明することができた。)
イオン対の場合では (Nature 404, 256-259, 2000)、彼らは 人為的に操作可能な外電磁場によって イオンを継続的に イオン(パウル)トラップに捕捉した状態を利用している。
そして、安定的な レーザーパルス源を用いて、そのイオン対を同時に振動させているにすぎない。
Fig.1. これは本当に”神秘的な”エンタングルメント状態なのか??

Fig.1 では、ベリリウムイオン (Be+) の 原子核のスピンを利用して、ラマンレーザー光線をそれらに照射している。
2つのイオン粒子は、 同時に 2つの超微細構造 (hyperfine structure)レベル (a と b) の間で 周期的に変化している。
これは、微小時間ごとに レーザー光線照射を変化させることによって可能である。
それらは古典力学的な視点からすれば 単に周期的に変化しているにすぎないのに、量子力学の物理学者達は、それらの状態は 確かに ”エンタングルメント”状態を意味している と主張しているのである。
(ここには 何の”神秘的な”ことは生じていないのにも関わらずだ。)
量子力学の物理学者達は 振動、回転、変化などの "リアルな"運動を とても忌み嫌う。
そのかわりに、”重ね合わせ (superposition)”という語を好んで使いたがる傾向がある。
つまり、量子力学は 我々を ”意図的に”多世界の重ね合わせ状態 に引き込もうと必死な気がしてならない。
Fig.2. 単なる振動 (oscillating) vs. 重ね合わせ (superposition)。

この重ね合わせの視点からすれば (各 Be+ イオンにおいて up と down の混合状態 = Eq.2)、これら2つのイオンが同時に運動すること (=Eq.1) は "神秘的な"エンタングルメントを意味しているのである。
しかし、実際には 古典的な意味合いからすれば、それらは 単に周期的に同時に変化しているにすぎないのである。
(Eq.1) 物理学者達はこれをエンタングルメントと主張している。

(Eq.2) ランダムな重ね合わせの混合状態。

重要な点は これらの Be+ イオンは 量子力学の 多世界様の重ね合わせでもエンタングルメント状態でもないということである。
各イオンの核のスピン状態を知るには 何らかの検出用のレーザーをそれに照射する。
そして はね返ってきた 光子を 少なくとも 50 から 60 カウント検出しなければ、各スピン状態を決定できない。
また エンタングルメントを判断するには、この操作を たくさん繰り返して統計を取る必要がある。
つまり このイオン対の量子もつれ実験は 2つの光子のもつれを調べた オリジナルのエンタングルメントとは 本質的にまったく異なるものである。
要するに、この実験は 単なる 古典的な統計結果の平均値 を調べただけで、不気味なリンクそのものを調べたわけではない。
(Fig.2') 50-60 光子検出必要 → 量子エンタングルメントとは関係ない。
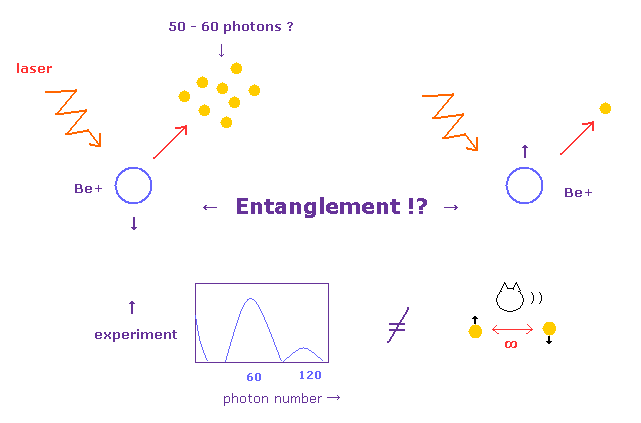
2つのベリリウムイオン (Be+) は パウルトラップ の軸上に 上下の振動数 5MHz でトラップされている。(Nature 409, 791-794, 2001)
(パウルトラップはペニングトラップに似ているものである。ペニングトラップに関しては このページを参照のこと。)
この2つのイオンは 約 3 μm 離れている。
超微細構造は 微細構造よりも かなり小さく、それは 核スピンと 電子スピン (= ボーア磁子) などの別の内因性の電磁場との相互作用によって生じる。
(もちろん ボーア模型においても 原子核の回転 (= スピン) は存在する。その質量が重いため 自転スピードは 光速を越えることはない。)
トラップされたイオンの超微細構造は 量子コンピューターなどの qubits に利用される。
なぜなら 長い寿命という利点があるからである。
超微細構造のエネルギーレベルだけ異なる 2つのレーザーパルスのペアによって、それらを遷移させる。
Be+ イオンの原子核の角運動量は -3/2 である。そのため 価電子の 2S1/2 の準位は次の2つのレベルに分離される。
(しかし 核磁子自体は ボーア磁子に比べてかなり小さいので、核の磁気モーメントはかなり小さい。)
(Eq.3) 超微細構造の down 状態。

ここで F は 全角運動量の量子数、mF は その角運動量の 外磁場によって量子化された方向への投影である。
( down 状態では mF = -3/2 - 1/2 = -2 となる。Fig.1 の (a) も参照のこと。 )
(Eq.4) 超微細構造の up 状態。

up 状態では mF = -3/2 + 1/2 = -1 となる。 Fig.1 の (b) も参照のこと。
これらの実験では Be+ イオンにおいて 2S1/2 と 2P1/2 (もしくは 2S1/2 と 2P3/2) の間の遷移を利用している。
Be+ イオンにおいても、2S1/2, 2P1/2, 2P3/2 という共通の名称は使われている。
しかし実際には Be+ のこれらの状態は 水素原子のものとは まったく異なるものである。
( Fig.3 もしくは Phys. Rev A 31, 4, 2711-2714, 1985 を参照のこと。 )
Fig.3. Be+, H, Na における奇妙なエネルギー準位の違い。
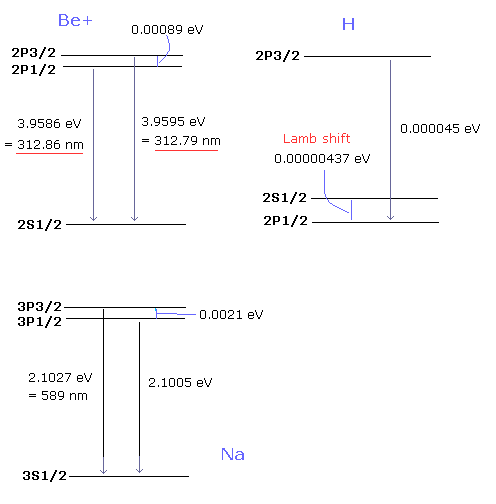
( 2.328 eV = 532.0 nm = 18794 cm-1 )
水素原子では、2S1/2 と 2P1/2 は ほとんど同じで、その間のごく微小なエネルギー差は "ラムシフト" と呼ばれている (= 0.00000437 eV)。
(ラムシフトは幻想か?も参照のこと。)
しかし、Be+ イオン や ナトリウムでは、これらのエネルギー準位は 水素原子に比べて 不自然なぐらい大きい。
( 0.00000437 eV (H) → 3.9586 eV (Be+) !)
量子力学の物理学者達は 2S (もしくは 3S ) の電子は 1S の電子の殻を突き抜けていくため、そのエネルギー準位は 2P に比べてかなり低くなると言っている。
一方で、ナトリウムなどにおける”繊細な”異常ゼーマン効果においては、彼らは まったく 内殻の電子の影響を考慮していないのである!
( このページも参照のこと。)
つまり、矛盾したことを言っていることになる。
また 水素原子では 2S1/2 のエネルギー準位は 2P1/2 よりも少し高い。
しかし Be+ イオンやナトリウムにおいては、2P1/2 が 2S1/2 よりもかなり高くなっている。
量子力学の物理学者達が あまりにも 2S1/2, 2P1/2, 2P3/2 などの形式にこだわりすぎていると思わないだろうか?
まず 最初に 単一電子の水素原子と 多電子原子を区別することは当然のことである。
例えば、外殻電子のスピードは 遅いため、内殻電子と公転周期が異なっている。
ある時は 外殻電子は内殻電子に近く、ある時は 少し離れている状態が考えられる。
これらの状態の違いで 小さいエネルギー準位差が生じても不思議ではない。( このページも参照のこと。)
遷移に使用される 2つのレーザー光線 (Fig.4 の R1 と R2) は 313 nm 近く (Fig.3 も参照のこと) の波長をもち、その振動数の差は 超微細構造レベル (ω は 約 2π × 1.25 GHz ) となっている。
Fig.4. Be+ イオン のエネルギー準位。
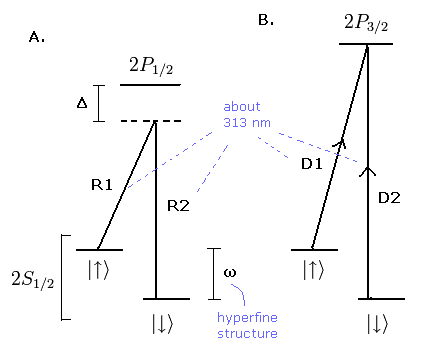
ここでは 2P1/2 の準位が Fig.4 に描かれているが、これは実験には表れない 仮想の準位である。
また、この実験では Fig.4 の R1, R2, D1, D2 すべての 遷移に 313 nm 近くのレーザーを使用しているようである。
まず最初に、Be+ イオン を冷やして それら両方を spin-down 状態にする。これは 基底状態 を意味する。
(Fig.1 もしくは Fig.5 の (a) を参照のこと。)
Fig.5. Be+ イオン の 超微細構造準位。
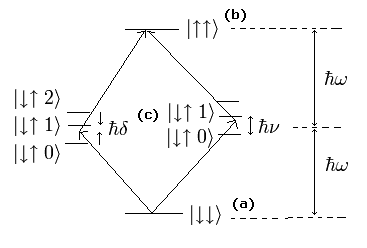
次に ω の振動数のレーザーをあてて Fig.5 の (a) から (b) への 2段階の遷移を起こさせる。
Fig.5 の (c) のエネルギー差は小さいため、十分な時間 2段階遷移を起こさせれば、Eq.1 のエンタングルメント状態が形成される。
(Nature 404, 256-259, 2000)
(彼らは、1つのみでなく 2つのイオンを同時に励起させるだけの 十分なエネルギーを照射している。)
(Eq.1) エンタングルメント状態か?

繰り返すが、Eq.1 のこの状態は 単に "人為的に" 振動させているだけで、”神秘的な”エンタングルメント状態とかでは まったくないと感じるのは私だけだろうか?
( あなた達は どう思われるだろうか? )
円偏光のレーザー光線 (Fig.4 の D1 と D2) を照射させることによって、各 Be+ イオン が up (Eq.4) か down (Eq.3) か 判定することができる。
up か down かの状態に応じて 蛍光の明るさに違いがあるからである。
次に Be+ イオン においても ベルの不等式が破れているかどうか調べることにする。(Nature 409, 791-794, 2001.)
しかし 光子の場合と異なり、Eq.1 を エンタングルメント状態と見なした時点で、この答えはすでにでている。
そのため 後は 形式的に ベルの不等式 (CSHS-type) が破れている状態で表現しなおすだけである。
この論文では、最初に Eq.1 の エンタングルメント状態の Be+ イオン のペアを用意する。
次に、各粒子に独立に古典的な操作 (manipulation) を施す。
これらの操作は φ1 または φ2 と表記される。
(この実験では、この操作は 位相変化 φ1 または φ2 を イオン1 もしくは 2 にそれぞれ生じさせる レーザー波を意味する。)
最後に、検出用レーザーを照射させて Be+ イオン が up (Eq.4) もしくは down (Eq.3) かを測定する。
これらの結果の関係式は次のように表せる。
(Eq.5)

ここでは Nsame と Ndifferent は それぞれ 2つのイオン状態が同じ (= up,up + down,down) か 異なる (= up,down + down,up) 結果の検出回数を意味している。
光子の場合では これらの変数 φ は 偏光フィルターの角度を意味していた。
また Be+ の up か down のかわりに、光子がフィルターを 通過 もしくは 反射したかを測定していた。
( このページでは 詳細に CHSH-type のベルの不等式を説明しているので、まず最初にこちらを参照するといい。)
実際に 次のベルの不等式が破れているか調べる。
(Eq.6)

Eq.1 のエンタングルメント状態にした後に、
(Eq.1)

次の位相変化 (= 操作) を 各イオン j (j=1, 2) に生じさせるように 微小時間だけ ラマン光線を照射させる。
(Eq.7) 操作

ここで 位相 φj は イオンj の位置における ラマン遷移をおこす場の位相を意味している。
Eq.7 の 操作によって Eq.1 のスタート状態を 次のように変化させる。
(Eq.8)

Eq.7 を Eq.1 に代入させることによって Eq.8 を導出できる。
ここで 次の演算子を作用させる。
(Eq.9)
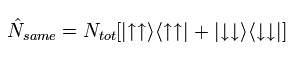
と
(Eq.10)
 ,
,
すると、Eq.5 の correlation function は 次のような結果になる。
(Eq.11)
 ,
,
Eq.6 の ベルの不等式は ある 位相の組み合わせのときに 最大限に破られる。
その1例は、次のような組み合わせである。
(Eq.12)

Eq.12 の 実験結果は B = 2.25 であり、これは Eq.12 と少し異なる。
しかし、この結果は 局所実在性の条件 B < 2 を破っている。
光子の場合は、光子AがフィルターAを通過した瞬間に、光子Bの偏光角が フィルターA (フィルターBでなく) と同じになる。(=エンタングルメント)
(光子AがフィルターAで反射した場合は、光子Bの偏光角はフィルターAに垂直になる。)
フイルターにでくわした後の これらの状態関係 (= 同じか垂直か) が Be+ イオンの Eq.1 の状態に相当する。
Eq.11 の correlation function において、我々は たった1つの変数 φ (= φ1 + φ2) によって表すことが可能である。
この φ は 光子における フィルターAとフィルターB の間の 角度の違い に相当する。
もちろん、Eq.7 の操作を 次の ランダムな重ね合わせ状態 に代入すると、
(Eq.2)

ベルの不等式は破ることはできない。
しかし、すでに述べたように Eq.1 の状態は 極めて"人為的に"用意された状態である。
なのに どうして 我々は この状態を 神秘的なエンタングルメント状態と 主張できるのであろうか?
それは 古典的な視点からすれば、単に 周期的に振動しているにすぎないのに。

2011/4/2 updated This site is link free.