トップページ (2電子原子も含む正確な新ボーア模型)
物性物理学のスピントロニクスは幻想である。
役に立たない量子化学での メカニズムとは?
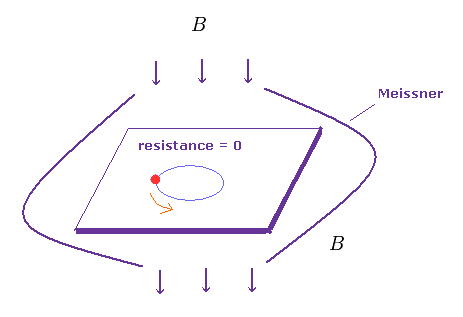
(Fig.1) 超伝導体

超伝導とは 電気抵抗がゼロになり、かつ 外磁場 (磁束) を完全排除する状態を言う。
金属などの様々な物質は ある臨界温度 (= Tc "転移温度"ともいう ) 以下 で このような超伝導状態になる。
普通、この臨界温度は 30 K (= ケルビン ) 以下であるが、高温超伝導では もっと高い。
このページに示したように、この磁場の排除する現象を "マイスナー効果" といい、これは 古典的な電磁気学で説明可能である。
(Fig.2) "フォノン" が 2つの電子を引き付ける?
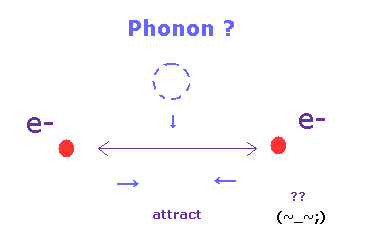
現在の微視的標準理論 (= BCS 理論 ) によれば、2つの電子は 互いにくっついて クーパー対という ボーズ粒子を形成することになっている。
驚くべきことに、これら2つの電子は 負の電荷を持っているにも関わらず、互いに 引き合うことができるのである。
この奇妙な引力は 準粒子 "フォノン" によって媒介される。
彼らは フォノンも電子と同じような フェルミ粒子であると主張しているが、もちろん、このフォノンは 実在の粒子ではない。
この非実在の粒子は 所謂 原子核や電子などの総合的な 格子振動を表しているとされる。
問題は 物理学者達は 決して このフォノンの具体的な正体を 決して問おうとしないことである。
この真理の追究を諦めた 困った姿勢が 現在の物性物理学の発展を 明らかに阻害していると言える。
(Fig.3) "ギャップエネルギー" (= Δ ) を 超伝導体に与える。 → 壊れる。
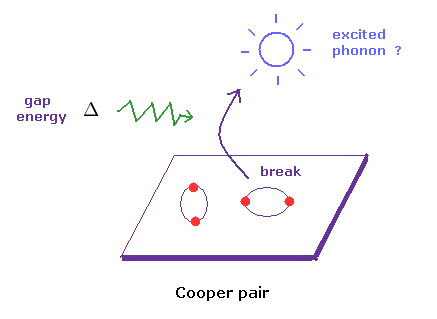
BCS 理論によれば、超伝導と常伝導状態の間には ある "エネルギーギャップ" (= Δ ) が ある。
そのため そのギャップエネルギーを 超伝導体に与えると、フォノンが
励起され 検出されるとしている。
もちろん、非実在のフォノン自体は 検出することはできない。
ただ 電子の流れである微小電流などを検出するだけである。
この事実にも関わらず なぜ彼らは 半ば盲目的に この仮想のフォノンなるものを 信じているのだろうか? 奇妙である。
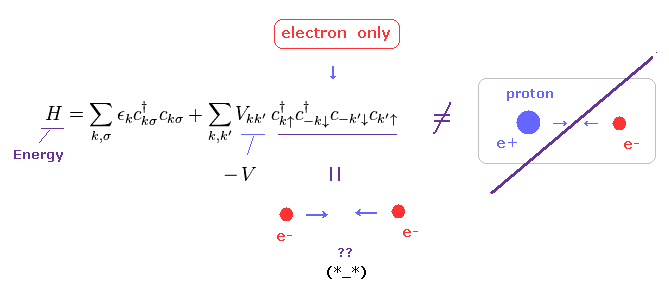
(Fig.4) 原子核なし。 電子だけで互いに引き合える? ← 不可能。
彼らは パウリの排他原理における 不思議な反発力について 決して具体的に解明しようとしない。
よって 粒子を表現するのに、非常に抽象的な 数学上の 生成 (= c† )、消滅 (= c ) 演算子 しか 利用できない。
Fig.4 に示すように、 これらの 抽象的な記号のみを用いて 現実の複雑な現象を すべて表すのは どう転んでも不可能である。
重要な点は、BCS理論における ポテンシャルエネルギー (= V ) は 正電荷の原子核を まったく含んでいないのである。
このハミルトニアン (= 全エネルギー ) には、 負電荷の電子 (= c†, c ) しか 含まれていないのである。
正電荷の 原子核が まったくない状態で どうやって これらは引き合うことができるのだろうか? 不可能である。
つまり、このポテンシャルエネルギー V は 非現実的で 実際の実験で 観測できないものなのである。
結果的に この非実在的な前提仮定が 現在の理論を もっと複雑な高温超伝導などの現象に 容易に拡張できない 主要な妨げになっている。
(Fig.5) 人為的な数学上の定義 = 準粒子。
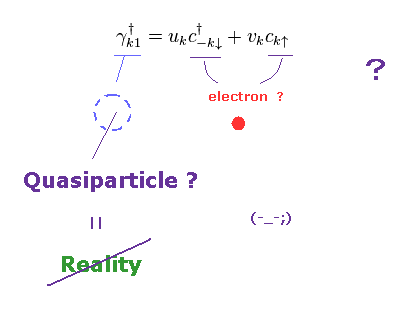
実は、このフォノンは 自然な概念とは 到底 言えないものなのである。
この準粒子は 非常に人為的な定義によって 導入された。
Fig.5 に示したように、フォノン以外にも BCS 理論は 人為的な 準粒子 (= ボゴリューボフ粒子 ) を必要とする。
この準粒子は 何と 生成因子 (= γ† ) は 電子の 生成 (= c† )、 消滅 (= c ) 演算子の組み合わせから成る。
つまり この架空のフェルミ粒子 は 実在するものではなく、実験値に近い値をだすためだけの目的で導入されたものである。
(Fig.6) ↓ エネルギーギャップ ?
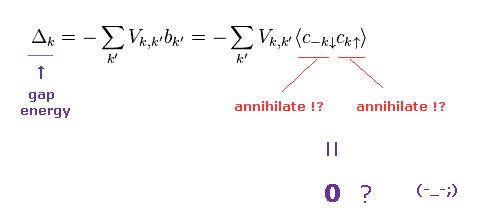
標準的な BCS理論は 強結合超伝導体や 高温超伝導体を除く 様々な実験結果を説明できるとされている。
この中で BCS が予測する最も重要な概念は "エネルギーギャップ" = Δ である。
しかし Fig.6 に示したように、このエネルギーギャップとは 非常に不自然な概念なのである。
なぜなら それは 2つの消滅演算子のみから 構成されており、通常の場の量子論とは まったく性質が異なるものだからである。
( もちろん、彼らが この形式を エネルギーギャップとして選んだ 明確な根拠は まったくない。 )
再び、この Δ の人為的な形式は 実験値に近付けるためだけに 導入されたと言っていい。
さらに、後で説明するが、このエネルギーギャップとして 2つの異なる矛盾した形式が 必要になる。
つまり BCS理論は 実は 物理学的のみならず 数学的にも まったく 不合理な理論なのである。
(Fig.7) エネルギーギャップの温度依存性 (= 曲線 ) は BCS の証明になり得るのか?
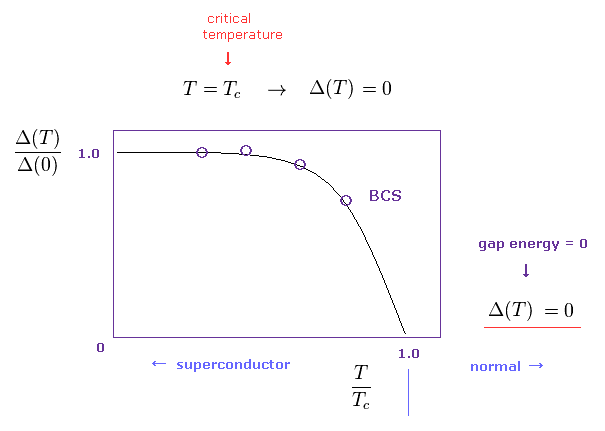
BCS理論は Fig.7 に示したような エネルギーギャップの 温度依存性を 正確に説明できるとされている。
エネルギーギャップ Δ(T) は 温度 (= T ) が高くなるにつれて 減少していく。
そして 臨界温度 (= Tc ) において このエネルギーギャップは ゼロになる。
BCS理論によれば、このエネルギーギャップは 超伝導体に特異的なものであるため、常伝導状態ではゼロになる必要がある。
後で説明するが、Fig.7 の曲線は "意図的"に導入されたもので BCS の自然な帰結ではない。
(Fig.8) 常伝導状態でも ギャップ? → BCS 理論が破綻。
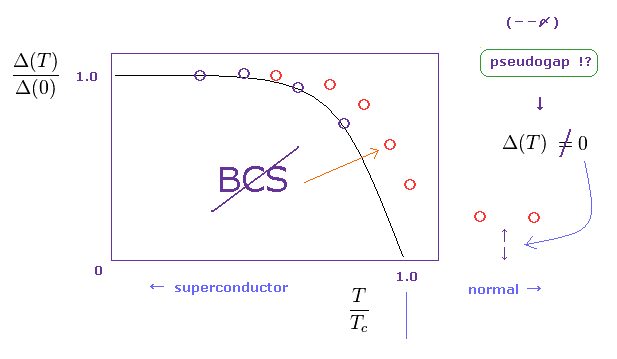
実は 現在までに BCS 理論が適用できない 超伝導体が 非常にたくさん見つかっているのである。
その中の1つに 常伝導体における 擬ギャップ というものがある。
Fig.9 で述べたように、エネルギーギャップというのは 超伝導体と常伝導体の間の バリア みたいなものである。
よって 標準の理論では このエネルギーギャップは 常伝導状態では 存在し得ないものなのである。
しかし 様々な物質において、何らかのエネルギーギャップが 常伝導状態においても 見つかっている。
さらに、これらの奇妙な超伝導体では、Fig.7 のようなギャップと臨界温度の関係式が
成り立っていないのである。 ( Fig.8 の赤い○ )
つまり 非実在のフォノンに頼る BCS 理論は すでに 破綻している。
(Fig.9) エネルギーギャップ (= Δ ) が 異なった方向で変化する?
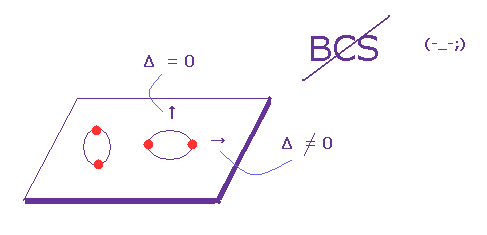
Fig.7 に示したように、 BCS理論では エネルギーギャップは すべての物質で 普遍的に 臨界温度に依存していると主張している。
しかし 多くの超伝導体で、このエネルギーギャップは 同じ温度の状態で 違った方角に依存して
変化するという奇妙な (= むしろ こっちが普遍的な ) 性質を示す。
これを "異方性" のエネルギーギャップという。
これらの物質において、異なった地点において エネルギーギャップが ゼロになったり ならなかったりするところがある。
彼らは "d 波" や "p 波" の超伝導体という新たな概念を導入して対処しようとしているが、この異方性は 明らかに 従来の BCS理論が すでに破綻していることを示している。
(Fig.10) 多くの物質は BCS 理論に従わない。
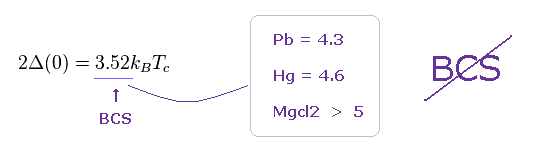
BCS理論が予言する最も有名な関係式は T = 0 での エネルギーギャップ (= Δ(0) ) と 臨界温度 (= Tc ) の関係である。
Fig.10 の 比 "3.52" が BCS の理論値である。
しかし 後で説明するが、BCS 理論は 様々な 粗い近似に頼っている。
つまり BCS による これらの予測値は 通常の超伝導体においても そんなに精密なものではない。
また、Pb、 Hg、 Mgcl2 ... などの 多くの超伝導体では これらの値は BCS の理論値よりも 大きくなる。
(Fig.11) 比熱の関係式は BCS 理論を満足しない。
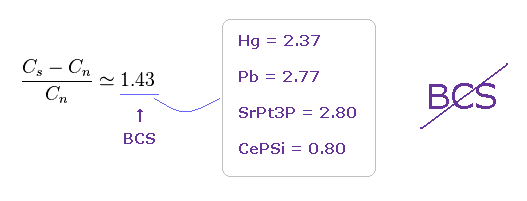
常伝導体 (= Cn ) と 超伝導体 (= Cs ) での 比熱の比は BCS 理論によれば、 "1.43" になる。
しかし この予測値においても、様々な超伝導体では 2.37, 2.8, 0.80 .. などの
まったく異なる値になる。
つまり非実在の "フォノン" に頼る BCS理論は 様々な物質において すでに 破綻しているのである。
(Eq.1) 意図的な計算ミス → BCS 理論は間違い。
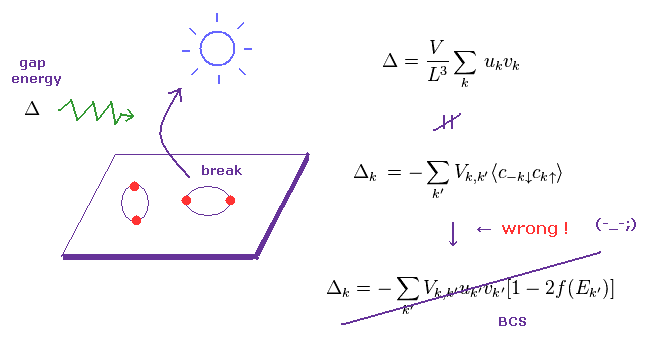
すでに述べたように、エネルギーギャップ (= Δ ) は BCS 理論が予測する最も重要な概念である。
つまり BCS理論が 偽りか そうでないかは このエネルギーギャップの定義に 完全に依存している。
実は、このエネルギーギャップの形式の決定に際して BCS理論は 意図的な 計算ミスをしているのである。
Fig.10 の比を得るには 2つの異なった形式のエネルギーギャップが必要になる。
( もちろん、これらの Δ の定義自体 まったく 人為的に導入されたものである。 )
Trick-1 で示したように、真ん中から 一番下の式への移行は 完全な 間違いである。
これが BCS理論のトリックの本質である。
(Trick-1) トリック = BCS 理論に不要な項の切り捨て。
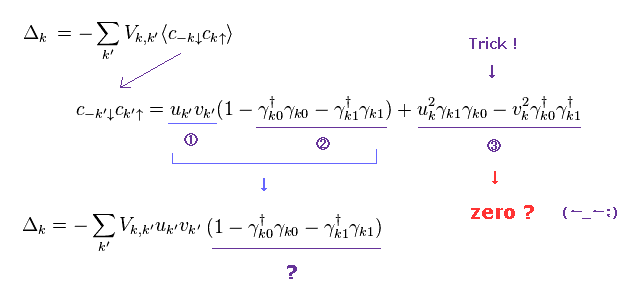
Fig.5 のように、 仮想の準粒子 (= γ ) を 電子 (= c ) から 生成した。
結果的に エネルギーギャップ Δ は Trick-1 の真ん中の式のようになった。
ここで 彼らは 突然 最後の2つの項 (= 3 ) を 削除してしまった。 ← Trick !
色んな教科書やウェブサイトを見る限り この 人為的な操作に対する 納得のいく説明を まったく見つけることが できない。
( むしろ 多くの教科書は このトリックを 隠しているように 見受けられる。 )
このことに関しては 後のセクションで詳しく説明する。
(Trick-2) トリック = 特定の "c" の項のみ γ (= 準粒子、quasiparticle ) に変える。

Trick-2 では、 彼らは 赤線の項の "c" と "c†" のみ "準粒子" (= γ ) に変更した。
一方で、最後の項に含まれる "c†" は 元の状態に放置したままで (= 青線 = "b*" )、 "準粒子" (= γ ) に 置き換わっていない。
この新しい演算子 "b*" は 明らかに この人為的なトリックを 隠すために導入されたと言っていい。
( つまり Trick-2 では 最後の項のみ 不要として 無視しており、これは奇妙である。 )
これはつまり 彼らは 意図的に BCS理論にとって 便利な項のみを 選んでいるのである。
特定の項のみの 人為的な選択は 明らかに トリックの1つであり、BCS理論が 自然な仮定を基にしていないことの証しである。
(Eq.2)
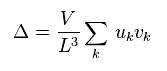
最初に Eq.2 のように 絶対温度 ( T = 0 ) での エネルギーギャップを定義した。
"V" は 電子間の 相互作用エネルギーの大きさを表す定数である。
"u" と "v" は ある実数。
L は 1辺の長さである。
(Eq.3)
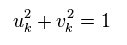
彼らは "u" や "v" を Eq.3 や Eq.4 のように定義した。
(Eq.4)
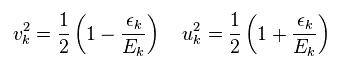
ここでは
(Eq.5)
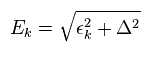
もちろん、 Eq.2 や Eq.3 の定義は まったくの人為的なものである。
どうして Eq.2 の形式の相互作用エネルギーにしたのかという 具体的な理由は まったくない。
これらの定義は 実験値に近い ある値を得るためだけに決めた形式と言っていい。
Eq.5 では、 Δ は "エネルギーギャップ" で、 εk は、
(Eq.6)
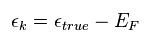
εk は 本当のエネルギーと フェルミエネルギー (= EF ) の差である。
この εk がゼロのとき、それはフェルミエネルギーに等しくなる。
(Fig.12) フェルミエネルギーは 非常に曖昧な概念である。
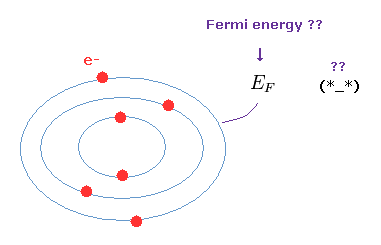
物性物理学では 頻繁に フェルミエネルギー (= EF ) という概念を利用する。
このページに示したように、現在の量子化学は 具体的な 電子状態を 示せない。
それらは 単に 行列などの数学を示すだけである。
そのため 彼らは 非常に荒い近似的なモデルに頼らざるを得ない。
軌道は 低いエネルギー準位から順に埋まっていく。
各軌道は パウリの排他原理のために 2つの電子までしか含めない。
最も外側の高いエネルギーレベルを "フェルミレベル ( エネルギー )" という。
フェルミレベルの これらの電子は 他の電子ですでに埋まった 内殻の軌道に
入ることができない。
残念ながら これらの概念には まったく明白な物理的イメージが存在しないと言っていい。 非常に 抽象的で 実用性に乏しいものである。
(Eq.7)
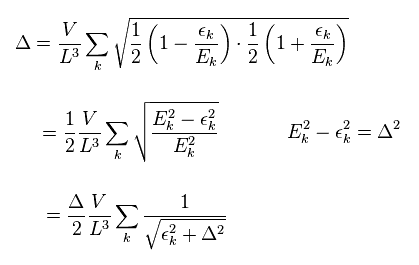
Eq.4 を Eq.2 に代入して Eq.7 を得る。 ( Eq.5 も使って。 )
Eq.7 の両辺を Δ で割って、次を得る。
(Eq.8)
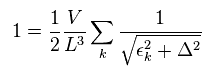
ここで とびとびの波数 "k" (= 運動量、エネルギー ) を連続にする。
(Eq.9)
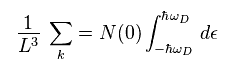
Eq.9 では、 N(0) は 電子密度で、ħω は 準粒子の最高エネルギーである。
Eq.9 を用いて、 Eq.8 は
(Eq.10)
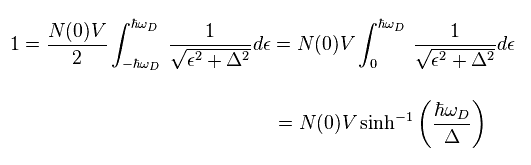
ここで 次の公式を使った。
(Eq.11)
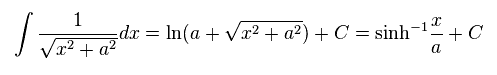
ここでは
(Eq.12)
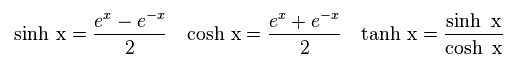
N(0)V が 非常に小さいと仮定すると Eq.12 の e-x は ゼロになるため 次を得る。
(Eq.13)
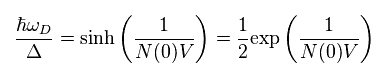
ここでは
(Eq.14)
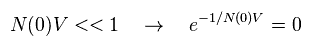
結果、最初の重要な関係式を得る。
(Eq.15)
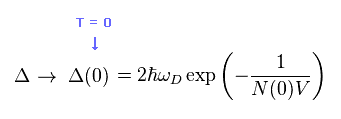
すでに述べたように Eq.15 の関係式は 絶対温度ゼロ ( Δ = Δ(0) ) のときのものである。
また Eq.2 と Eq.3 の人為的な定義によって Eq.15 の最終結果に つながった。
(Eq.16)
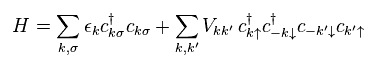
彼らは BCS ハミルトニアンを Eq.16 のように定義した。
" ↑ ↓ " は 各電子のスピンの方向である。
2つの電子のペアの 全運動量を ゼロと仮定する。
よって 1つの電子の運動量が "k" のとき、もう1つは "-k" になると 彼らは主張している。
"V" は クーパー対での 運動量 k と k' 間の 遷移 (= 相互作用 ) ポテンシャルエネルギーである。
驚くべきことに、このポテンシャルエネルギーには まったく 正電荷の原子核が
存在しないのである。 (= 電子のみ )
しかし 彼らは これらの負電荷の電子同士のみで 互いに 引き合えると主張している。これは奇妙である。
(Eq.17)
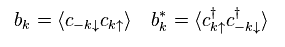
ここで Eq.17 のように 演算子 "b" を定義する。
"†" は 複素共役の意味である。
(Eq.18)
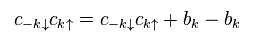
Eq.17 と Eq.18 を Eq.16 に用いると、次のハミルトニアンを得る。
(Eq.19)
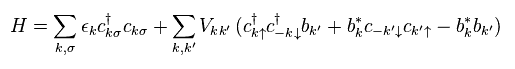
Eq.19 を得る過程で、 ある トリックを用いている。
彼らは 任意に " c c† " もしくは " b b* " を 演算子として選んでいるのである。
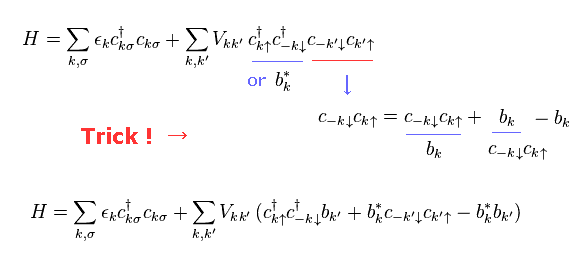
ここで エネルギーギャップ Δ を 次のように定義する。
(Eq.20)
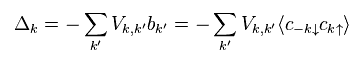
奇妙なことに、このエネルギーは 消滅、消滅演算子 (= c c ) のみ で構成されているのである。
これはつまり ギャップエネルギーは 常に ゼロになってしまうということだろうか ? ( 生成演算子ないから。)
もしそうなら、BCS の予言は 間違いということになる。
Eq.20 を Eq.19 に用いて、次を得る。
(Eq.21)
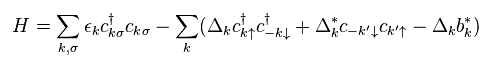
Trick-2 と Eq.19' では、 Eq.21 の最後の項 (= Δkb* ) も "c†" の演算子で構成されている。
しかし 彼らは この最後の項のみ 人為的に無視してしまうことになる。
これは BCS理論における 重要なトリックの1つである。
(Eq.22) c = 電子、 γ = 準フェルミ粒子 ?
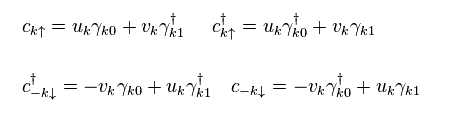
Eq.22 では、 γk0 と γk1 は それぞれ 仮想の 準粒子 "1" と "2" である。
Eq.22 の関係式は 次のようにも表せる。
(Eq.23)
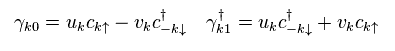
Eq.23 を Eq.22 に代入すると、 Eq.22 と Eq.23 が 同じ関係式であることが分かる。
ここで 電子 (= "c" ) が 次の 反交換関係を満たすと仮定する。
(Eq.24)
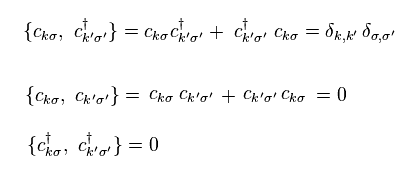
もし Eq.24 が成り立つと、準粒子 γ も 次を満たす。
(Eq.25)
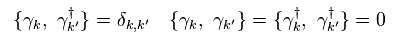
そのため 彼らは 仮想の準粒子 γ も "フェルミ粒子" だと主張している。
しかし このフェルミ粒子は あくまで仮想の準粒子で 非実在のものである。なぜなら
(Eq.26) 真空から 準粒子を消滅 → ゼロにならない !?
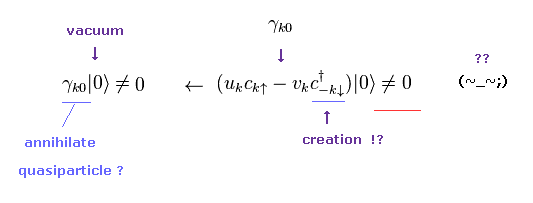
Eq.26 に示すように、何らかの準粒子の消滅演算子を 真空に作用させても この真空は ゼロに ならない からである。
( γ は 生成演算子 c† も含んでいることに注意。)
つまり この準粒子は 電子などの 通常のフェルミ粒子とは まったく 異なる物体なのである。
これが "準粒子" と呼ばれる所以である。
Eq.22 を Eq.21 の最初の項の "c" と "c†" に代入して 次を得る。
(Eq.27)
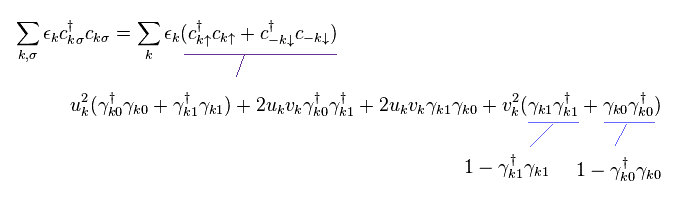
同様に、 Eq.22 を 残りの項 ( 最後の "b" の項を除いて ← トリック ) の "c" と "c†" に代入して それらをすべて足すと、Eq.21 のハミルトニアンは 次のようになる。
(Eq.28)
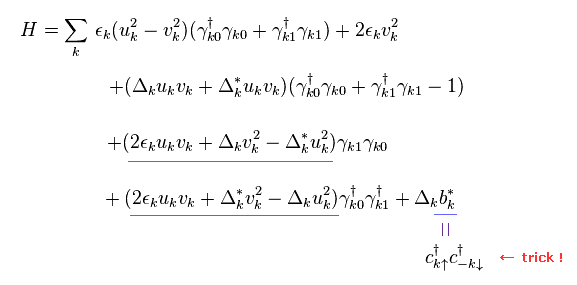
Trick-2 で述べたように、 "c†" の演算子が 最後の "b*" の項内に まだ残っているのである。
しかし 彼らは 最後の b* 内部の "c†" のみ Eq.22 を用いて γ に変換しようとしないのである。
これは明らかに理不尽で 人為的なトリックである。
彼らは Eq.29 が Eq.28 において 満たされていると仮定した。
(Eq.29)
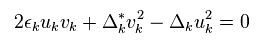
さらに 彼らは 人為的に 次を定義した。
(Eq.30)
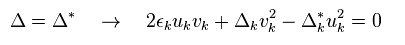
残念ながら Eq.30 の定義は 完全に間違いである。
なぜなら Δ は Δ* と等しくならないからである。
(Eq.31)
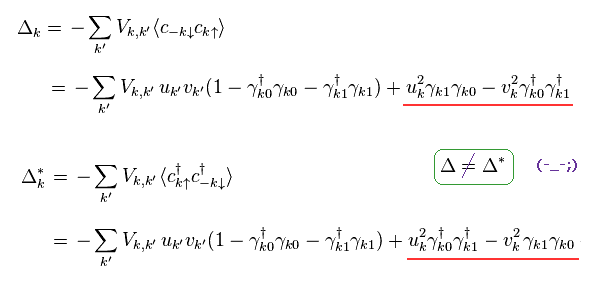
驚くべきことに、彼らは 最後の2つの項 (= 赤線 ) を 突如として 無視 (= 消去 ) してしまうのである。
これが もっとも重要なトリック (= Trick-1 ) である。
色んなウェブサイトや教科書か何かで探されると お分かりになると思われるが、この操作に 明確な根拠は まったくない。
Eq.30 は 完全に間違った式なのである。 ( 付録も参照のこと。 )
次の定義を用いて ( 付録も参照のこと )
(Eq.32)
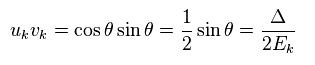
と
(Eq.3)
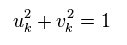
(Eq.4)
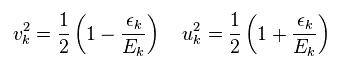
(Eq.5)
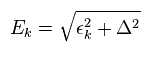
Eq.28 のハミルトニアンは 次のようになる。( Eq.29 と Eq.30 を用いて )
(Eq.33)
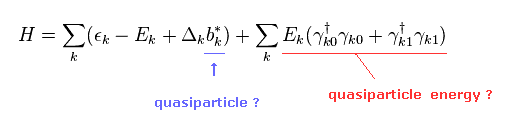
ここで 彼らは Eq.33 の 赤線は 準粒子のエネルギー (= E ) と 数演算子であると主張しだした。
そして 残りの項は "不要な" 定数として扱うことにした。
しかし Eq.17 を見て分かる通り、 この "b*" 項には まだ "c†" の演算子が 残っているのである。
結果的に Eq.22 の置きかえを用いて、この "b*" の項も 別の準粒子エネルギーになり、BCS の正式な結果を変えてしまうことになる。
しかし、彼らは 意図的に この項のみ 無視してしまった。
これも 重要なトリック (= Trick 2 ) の 1つで、現在の BCS理論が 間違いであることを示している。
エネルギーギャップ Δ は 次のように表せる ( Eq.20 を参照 )。
(Eq.34)
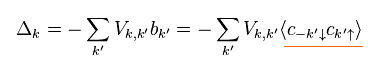
Eq.22 を Eq.34 に代入して 次を得る。
(Eq.35)
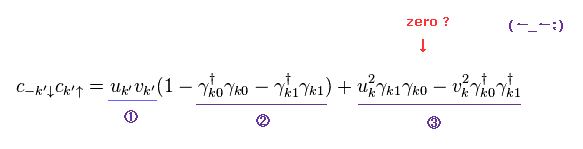
重要な点は、BCS理論では Eq.35 の 最後の2つの項 (= "3" ) のみ 密かに消去してしまうことである。
( この重要な事実は ほとんどの教科書やウェブサイトでは 隠しているようである。)
この操作は 非常に 理不尽で もちろん 完全に計算ミスである ( 意図的な )。
Eq.35 で "3" の項のみ消去する 正統な理由は何もない。
( 付録参照のこと。 )
次の フェルミ粒子の密度分布を 数演算子 (= γ† γ ) に代入する。
(Eq.36)
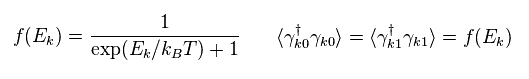
結果的に、
(Eq.37)
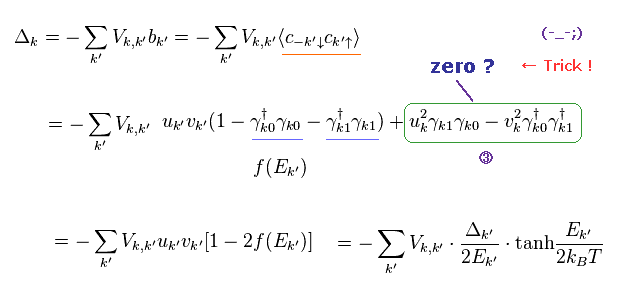
ここでは
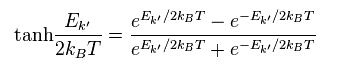
もちろん、この仮想のフェルミ粒子 は 実在しない。 ( Eq.26 も参照。)
つまり BCS理論には 何のリアリティーもないのである。
適切な結果を得るには "3" 以外の項のみ 残さなければならない。
Eq.37 の最初の式に示したように この Δ 自身、消滅演算子のみ (= "cc" ) から成っている。
つまり 最初から このエネルギーは 保存されず、ゼロに消えてしまうことになる。 これは奇妙である。
また "3" の項のみ消去することは 非常に 人為的なトリック (= Trick 1 ) である。
(Eq.38)
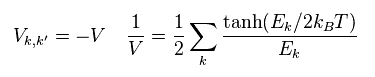
彼らは 相互作用ポテンシャル V を 定数 (= -V ) として定義した。
( つまり BCS理論は 非常に) 粗い近似なのである。 )
-V を Eq.37 に代入して、両辺を Δ で割って Eq.38 を得る。
ここでは とびとびの運動量を 連続の積分に変える。
(Eq.39)
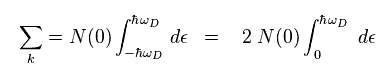
Eq.39 を Eq.38 に用いて、次を得る。
(Eq.40)
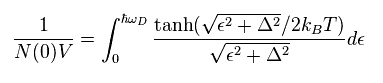
ここでは
(Eq.41)
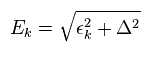
Eq.40 は BCS 理論の 直接的な結果である。
重要な点は 元の Eq.40 の式は 次の Eq.42 の関係式を 何も 表していないということである。
(Eq.42)
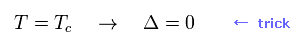
実験値に近づけるために、臨界温度 (= Tc ) で エネルギーギャップ Δ を ゼロにする必要がある。
彼らは Eq.42 の関係式を 人為的に Eq.40 に用いた ( 代入した ) 後に、それを部分積分して、
(Eq.43)

Eq.43 では、 彼らは "1" と 積分部分でのみ ħω を 無限大として扱った。
結果、臨界温度 (= Tc, Δ = 0 ) で、Eq.43 の近似的な結果を得た。
Eq.40 に示したように、元の結果は Tc のときの Δ について 何も言っていない。
(Eq.44)
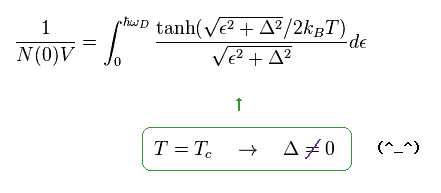
つまり Eq.43 は 自然な帰結では ない のである。
Ee.43 は 次のように変換される。
(Eq.45)
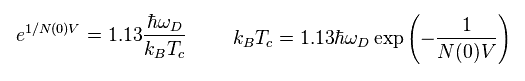
ここで Eq.15 の絶対零度での結果を用いる。
(Eq.15)
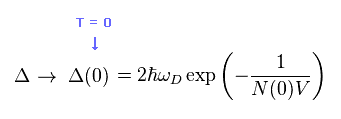
Eq.45 と Eq.15 から 次を得る。
(Eq.46) 予測。
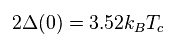
Eq.46 は エネルギーギャップ ( T = 0 での Δ ) と 臨界温度 (= Tc ) の関係を示す BCS理論の 重要な理論値である。
しかし Fig.10 で示したように、Eq.46 に従わない物質は たくさんある。
また Eq.46 を得るのに、彼らは 意図的な 計算ミス (= Trick 1, 2 ) をしている。
つまり Eq.46 の結果は 理不尽なものと言える。
ここで ボルツマン因子 β を定義し、Eq.40 の右辺に 2つの項を追加する。
(Eq.47)
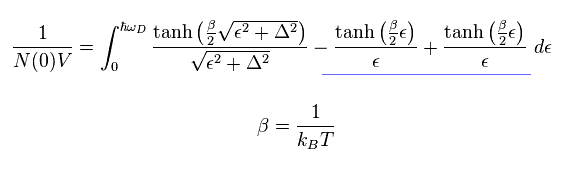
ここで Eq.43 の近似を 左辺と 右辺の最後の項のみに使用する。
(Eq.48)
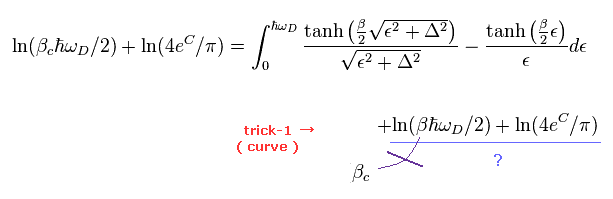
重要な点は Eq.47 (Eq.48) の最後の項の β 内の 温度 "T" は 臨界温度では
ないということである。
しかし 彼らは この最後の項においても 臨界温度での近似を用いた。
これも Δ が 臨界温度で ゼロに近付く結果を得るための トリックの1つである。 .
Eq.48 は、
(Eq.49)
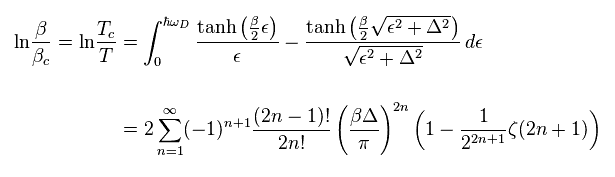
再び 次の近似を用いる。
(Eq.50)
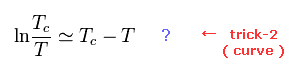
Eq.49 では、Δ が 非常に小さいと仮定して、 ( n=1 ) の項のみピックアップする。
Eq.50 も用いて、 Eq.49 は
(Eq.51)

Eq.51 を Eq.46 で割って、次を得る。
(Eq.52)
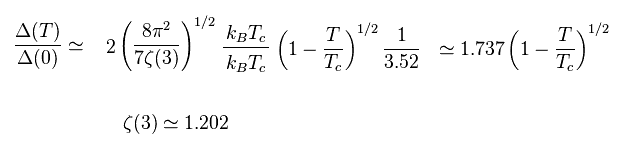
よって BCS理論は Fig.13 のような 曲線を 予測できたと主張している。
しかし Eq.48, Eq.50, Eq.51 の 近似は Fig.13 の曲線を意図的に得るためのものであることは明白である。

BCS の直接的 (= オリジナル ) の計算結果は Fig.13 のカーブを まったく 示していないのである。
(Eq.53)
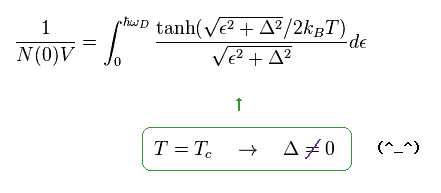
臨界磁場は 最も正確に測定できる値の1つである。
この結果によれば、臨界温度 (= Tc ) と比熱 (= Cs ) の関係式は
(Eq.54)
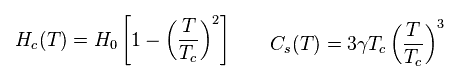
Eq.54 は BCS の予測する 指数関数的な変化とは 異なる。
(Eq.55)
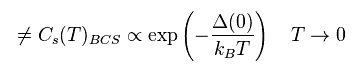
比熱の比は Eq.37 の BCS 理論から得られる。
すでに述べたように、これらの計算は 間違っており、 BCS 理論が 何も予測 できない ことを示している。
(Fig.14) 比熱の関係式は BCS 理論を満たさない。

実際に Fig.14 の関係式は 様々な超伝導体において 破れている。
(Fig.15) 無限小の トンネル電流の検出?
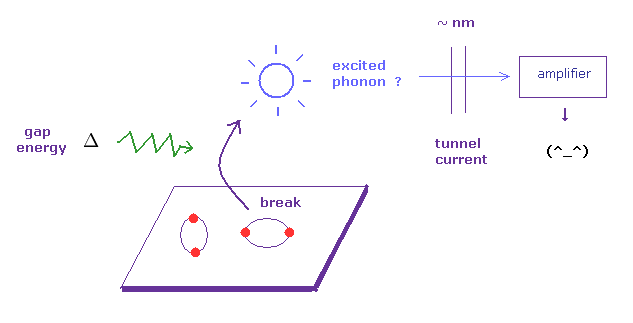
実は、超伝導体において エネルギーギャップ Δ を検出することは 非常に難しい。
何らかの 電位 (= エネルギー Δ ) もしくは 光を 超伝導体にあてて、フォノンを励起させる。
この励起されたフォノンは 小さなトンネル電流として検出できると 彼らは主張している。
( "トンネル" とは言うものの、各粒子は ナノメーター以上の距離のバリアを 通過することはできない。つまり 単に ドブロイ波の効果を表しているだけである。 )
しかしもちろん、この微小電流の 増幅器と検出器には 最小の 検出閾値が存在する。
この増幅器の設定を変えれば、臨界電位も 変化することになる。
この検出は 単一光子 (= "フィクション" ) の検出に 非常に似ている。
(Fig.16) トンネル電流を 完全にゼロにすることは不可能である。
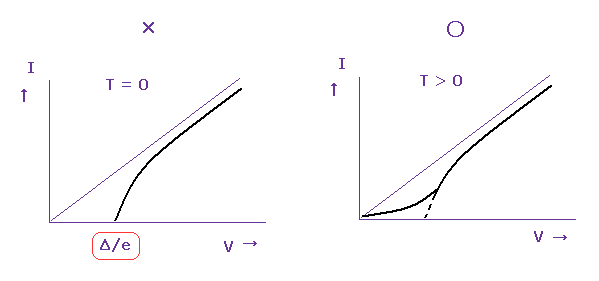
理論的には フォノンのエネルギー (= ε ) は 絶対零度 ( T = 0 K, Fig.16 左 ) で 完全にゼロになる。
しかし 完全な絶対温度ゼロ状態にすることは不可能である。
そのため 電位を まったく かけてないときでさえ、小さなトンネル電流が 常に 検出される。 (= Fig.16 右 )。
これも 誤差の原因である。
Aq.1 と Aq.2 の定義を用いて、
(Ap.1)
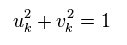
(Ap.2)
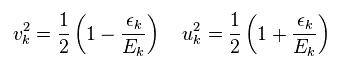
次を得る。
(Ap.3)
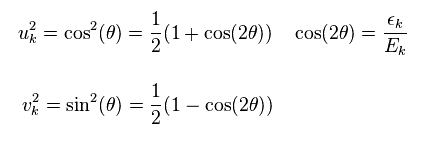
すると Eq.32 の結果を得る。
(Ap.4)
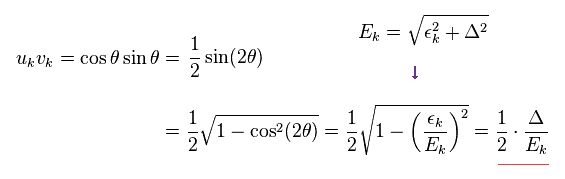
"準粒子" を Eq.23 (= Ap.5 ) のように定義する。
(Ap.5)
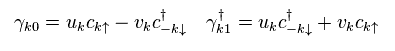
Ap.5 を用いて、この準粒子が 実在の粒子とは まったく異なる粒子であることを示せる。
なぜなら もし 消滅演算子 (= γ ) を 真空 (= |0> ) に作用させても この真空が Ap.6 に示すように ゼロに ならない からである。

そのため 彼らは 次のような 新たな 非実在的な 準粒子真空なるものを定義した。
(Ap.7) 準粒子 (= BCS ) の真空 ??
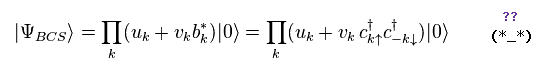
Ap.5 と Ap.7 を用いて、次を示せる。
(Ap.8)
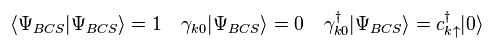
ここでは次を使う。
(Ap.9)
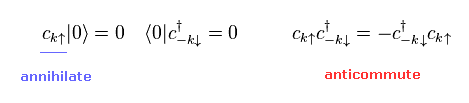
よって Ap.7 が 準粒子の真空であると見なせる。
もちろん この真空は 本当の真空とは違う。
なぜなら 電子の消滅演算子 (= c ) を作用させても ゼロに ならないからである。
(Ap.10)
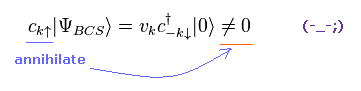
ところで、次の "b" の演算子を この準粒子真空で挟むと どうなるのだろうか?
(Ap.11)
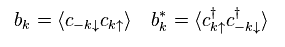
Ap.7, Ap11, 反交換関係を用いると、次を得る。
(Ap.12)
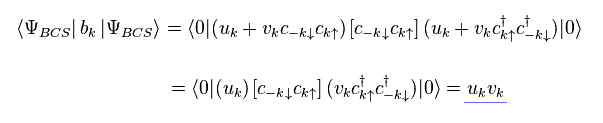
同様に
(Ap.13)
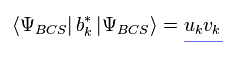
これが 彼らが Eq.30 で Δ = Δ* であると主張している理由である。
(Ap.14)
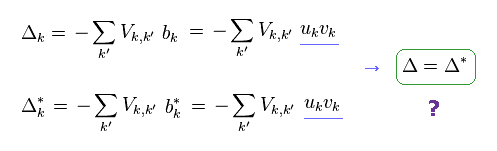
しかし実際は もし Ap.14 を満たすと、Fig.10, Fig.11 の BCS の理論値をだすことができない。
(Ap.15)
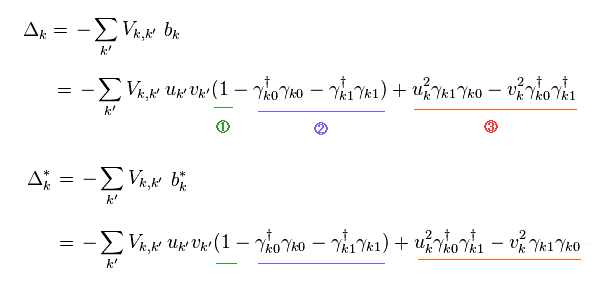
彼らは Ap.15 で "3" の項のみを消去して、 "1" と "2" の項を残そうとしている。
これは BCS理論の重要なトリックの1つである。
お気づきのとおり、この 人為的な選択は 通常の真空、準粒子真空の両方において、不合理で 完全に間違いである。
もし BCS真空が 1つの準粒子のみを含んでいたら "2" の項のみが残る ( "1" と "3" は消える。 ).
もし BCS真空が 2つの準粒子を含んでいたら "3" の項のみ残る。
つまり "1" と "2" の項のみ残るという操作は どう転んでも あり得ないことなのである。

2013/12/14 updated This site is link free.