♦ トップページ (2電子原子も含む正確な新ボーア模型) ♦
♦ 光子とベルの不等式 ♦
ボーア模型は 密度汎関数法よりも役に立つ
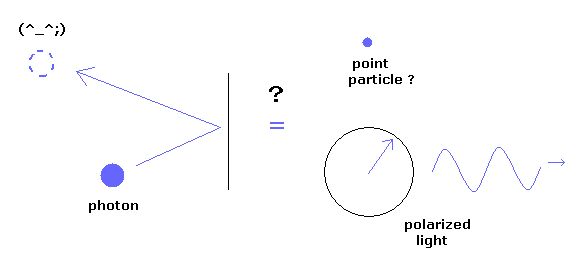
(Fig.1) 光子は 粒子 それとも 電磁波?

量子電磁力学によれば、単一光子は 点状粒子でなければならない。
しかし 実際の実験では、左、右円偏光、垂直、水平偏光の光などの 古典的な電磁波が使用されている。
彼らは 明らかに 古典的な光に特異的な性質を用いているにも関わらず 論文や何かで それを表す時 必ず 光子という粒子の表現を使おうとする。
Fig.1 に示したように、もし光が 点状の粒子だとしたら、それはどうやって 偏光したり 他の粒子と相互作用したりできるのだろうか?
つまり 光子という点状粒子の概念は 現実ではあり得ないものなのである。
(Fig.2) もつれた光子対?
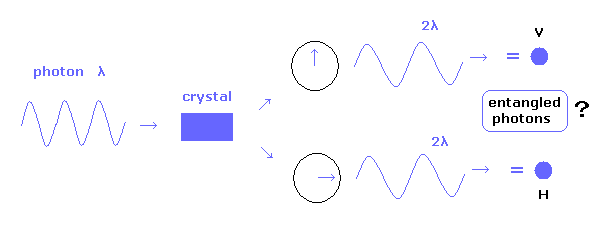
もつれた光子対は しばしば "パラメトリック下方変換" によって生成される。
この過程では 波長 λ の光子が ある結晶に入射すると、波長 2λ のペアの光子対に分離する。
そのため 全エネルギーは保存する (= それらの振動数は半分になる )。
生成された光子対の1つは 水平偏光、もう1つは垂直偏光である。
この光子対は 明らかに古典的な電磁波にも関わらず、彼らは必ず "光子"という用語を使いたがる。
(Fig.3) 光子という点粒子は 互いに干渉しあえるのか?
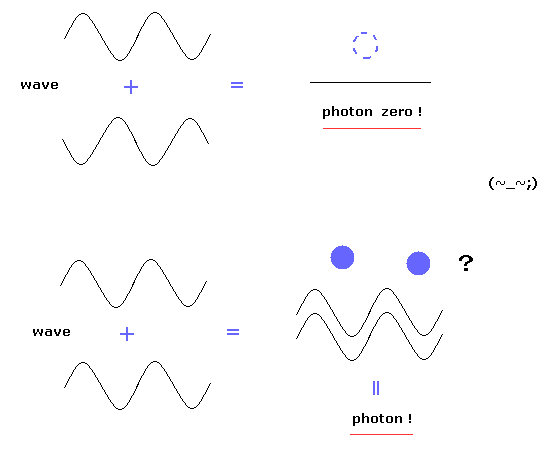
驚くことに、光子という点粒子は 彼らの実験によれば 互いに干渉し合えるのである。
Fig.3 上では、位相が逆同士の光子の干渉のため、光子は消えてしまう。
逆に Fig.3 の下では、位相がそろっている干渉のため 光子の数 (= 振幅 ) が増加すると 彼らは主張している。
しかし Fig.3 に示すように、これらの干渉現象は 彼らが言う "光子" の実態が 明らかに 古典的な波であることを示している。
(Fig.4) 単一光子検出器は 光子が粒子であることを示しているのか?
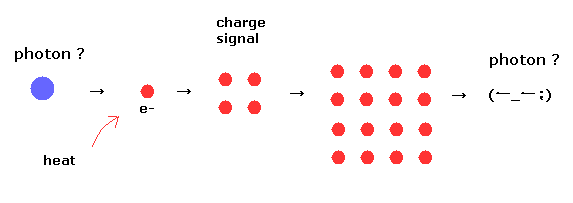
最初に 私たちは 単一の光子を直接 生成することはできない。
コヒーレントなレーザー光を弱めて 光子検出器で それらの電流信号を見ることによって、光子の存在を 推定しているにすぎない。
この検出器は 光子が入射したとき 必ず光子を検出できるわけではなく ( < 60% ) 、また dead time のため 単一光子と2つの光子の区別をつけることは不可能である。
もちろん 単一光子自体を直接見られないため、この光子という概念は 単に憶測にすぎない。
光電効果を繰り返すことによって、電流信号が増加していって はじめて 光子検出器が単一光子を検出できる。
これらの過程における光のロスを考慮すると、光の強さが ある一定の閾値に達しているとき、 光子検出器が 電流信号を示すと考えるのが 極めて自然である。
(Fig.5) マッハ・ツェンダー干渉計。
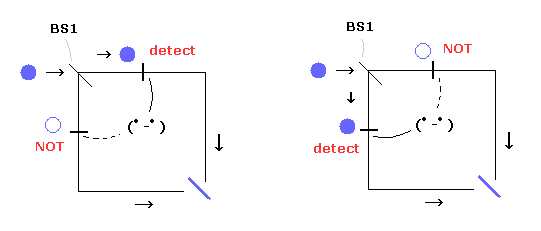
マッハ・ツェンダー干渉計では、1つの光子が ビームスプリッター (= BS1 ) で 2つの異なった経路に分離したとき、Fig.5 に示すように 同一時刻では どちらか一方の経路でのみ 1光子を観測することができる。
これはつまり 量子力学的な解釈によれば 単一光子は 2つの経路に分離していないということになる。
(Fig.6) 単一光子の干渉。
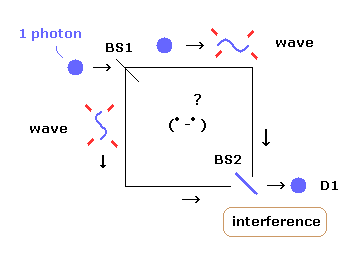
しかし これら2つの異なった経路からの 電磁波の干渉効果は 実際に観察されるのである。単一光子は 2つの経路のどちらか一方にしか存在しないはずなのに 奇妙である。
一般に この奇妙な現象は 1つの光子の 両経路への重ね合わせ現象によって生じるとされている。
この "重ね合わせ"という考えは 奇妙な多世界解釈そのものであり、はっきり言って 何のリアリティーもない。
( この場合は world A と world B ということになる。)
(Fig.7) 光子 = 古典的な電磁波。
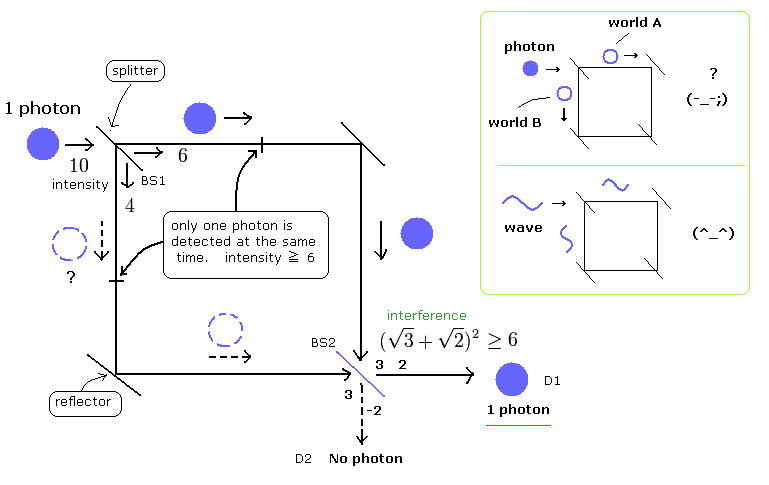
ここで光子を波として、その電磁波の強さがある一定の閾値(threshold)以上の時にはじめて光子検出器で光子1つとして認識されると仮定してみよう。
例えば、最初の1つの光子(電磁波)の強さを10としよう。
そしてそれをビームスプリッター ( BS1 ) で2つの経路に分離させるとしよう(例えば6と4に)。
そして、光子検出器では電磁波の強さが閾値6以上のときに初めて 単一光子として検出できると仮定しよう。
すると光の強さ10では光子2つ(=強さ12以上)としてではなく、光子1つとして検出されるということになる。
分離された光はというと、6サイドでは単一光子として検出でき、4サイドでは光子として検出されないということになる。
しかし、この6と4の光は干渉でき、最後に6以上になった方に光子が検出されるという、干渉効果も見事に説明できてしまう。
例えば、50/50 ビームスプリッター ( BS1 ) のとき、10の電磁波が5+5に分離された場合は両方の検出器で検出されない。
(この場合は光子の存在自体が認識されないので 無視されたケースとなる。)
光子を検出器で検出したとき はじめて、光子の存在を認識することができる。
50/50 ビームスプリッターというのは 基本的に 無偏光の光を 平均して 半分に分離するものである。
ビームスプリッター到着時点の光の偏光状態や振動数によって この確率は変化する。
(Fig.8) ビームスピリッター 2 ( BS2 )。
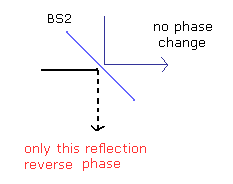
ビームスプリッター1 ( BS1 ) で分離後、ビームスプリッター2 ( BS2 ) においても 電磁波は ほぼ半分に分離される。
( 例えば、 6 → 3 + 3, 4 → 2 + 2 )
この実験では、ビームスプリッター2においては、下方向への反射のみ 光の位相が逆になるように設定されているとする。
( 通過光は変化しない。)
よって、D1の検出器側では、干渉によって 光の振幅が増加して 光子として検出することができる。
なぜなら、D1側では、光の強さが 干渉によって "必ず" 6以上に達するからである。
(光の振幅 (amplitude) は 光の強さ (intensity) の平方根であることに注意。)
[ D1側では、1光子が "必ず" 干渉によって検出される。 ]
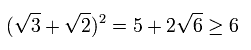
一方で、D2検出器側では、2つの経路からの 光の振幅が 互いに打ち消し合うため、光子として検出することができない。
(光の強さが D2側では、”6”に達することができない。)
[ D2 では 光子は検出されない。 ]
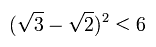
もちろん、最初の光の強度 "10" が ビームスプリッター1で 5+5 にちょうど分離された場合も 上記と同じ結果となる。
この場合は、光の強さ "5" は 2.5+2.5 にさらに分離されるため、D1側では、
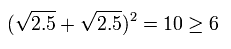
また D2 側では、
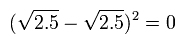
これらのケースでは、 全エネルギーが保存されている。 ( 10 → 10 ).
つまり、単一光子と複数のビームスプリッターを用いたマッハ・ツエンダー干渉計の実験は 電磁波としての光子によって十分説明可能なのである。
遅延選択量子消しゴムは本当の現象か? も参照のこと。
(Fig.9) 遅延選択実験。
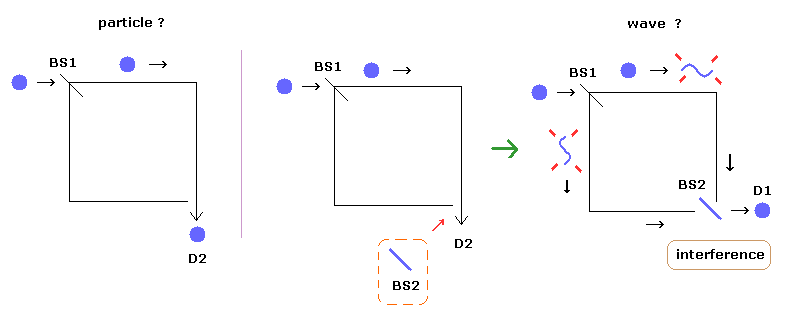
遅延選択実験によれば、単一光子が ビームスプリッター ( BS1 ) を通過後、2つの通路の片方のみに入る。
実際、光子検出器では 片方のみしか光子は検出されない。
しかし 単一光子が BS1 を通過後に 上記のように BS2 のスプリッターを通過すると、何と 両方の通路からの干渉効果が検出される。
( 光子は 片方の通路にしか入らなかったのにである。)
これは つまり 単一光子が BS1 を通過後の未来から 過去の出来事 (= 光子が波になるか粒子になるか ) を変更 (= 遅延選択 ) できることを意味しているのだろうか?
もちろん そんなことは不可能なので 光子という粒子の概念自体が間違いということになる。
( 残念ながら 一般の方々は これら奇妙な量子力学の側面をあまりご存じない。)
(Fig.10) 光子のスピンは 本当に " 1 " なのか?

1つの光子は ±1 のスピンを持つと言われている。しかし、この光子のスピン1とはいったい何なのだろうか?
一般の教科書には光子のスピン ±1 は左回転と右回転の偏光を持つ電磁波に相当すると書かれてある。そして、直線偏光はこの2つの回転偏光の重ね合わせ ( いわゆる superposition )によるとされている。
この”重ね合わせ”というのは曲者である。普通の直線偏光の光も”見方によっては”不思議な重ね合わせ状態の結果だというのだ。
つまり、”重ね合わせ”とは便利な数学的な技巧であり、いろんな場面で量子力学はごまかしのように利用している。
あるものの集合の一部分はある状態、もう一部分はべつの状態であるとき、これも重ね合わせということもできる。また、ある1つのものが目には見えない速度で振動しているときや、場合によっては単に静止しているときも”重ね合わせ”と言えなくはない。
結論からして、この”重ね合わせ”という現象は無意味以外の何物でもない。
(Fig.11) 微細構造 = 光子のスピン 1 ?
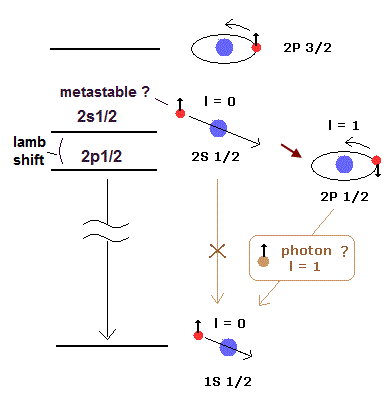
さて、そもそも光子のスピン1とはどのように発見されたのであろう?
1910 年代においては、水素原子の微細構造 は ボーア・ゾンマーフェルト模型において 2S と 2P の状態間の電子速度の違いによる相対論的エネルギーの差を表していた。
この計算結果は見事に実験値と一致していた。
電子スピンの出現以降、この微細構造の解釈がスピン・軌道相互作用(2P1/2 と 2P3/2 のエネルギーの差)に変わってしまった。このページも参照のこと。
偶然にもこの値は先のボーア・ゾンマーフェルト模型の値と一致した。(由来はまったくの別物なのに・・)。
すると、電子スピンのある水素原子では、2S から 1S への遷移は不必要になってしまい、実験値と合うようにするのは、これを抑制する必要がでてきた。
ここで、当時の研究者達は選択規則なるものを設けて、2S から 1S への遷移を勝手に抑制してしまった。そして、それは光子のスピンが1であることから説明できるとしたのだ。
すなわち、光子のスピン1とはきわめて人工的に作られたものなのだ。
(Fig.12) 点状粒子 が 光電効果 ?
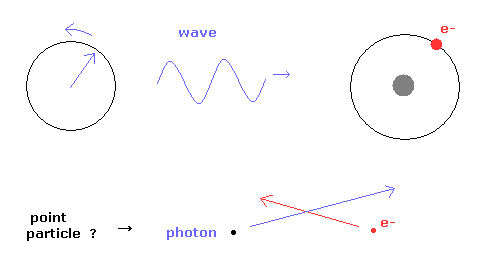
光電効果 などは、粒子としての光子でないと説明できないとされているが、果たして本当にそうだろうか?
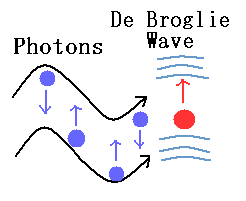
電子は常にその周囲にド・ブロイ波 を伴い、その波は電子の運動量と同調している。
つまり、光電効果やコンプトン散乱 などの場合、小さな小さな電子よりもむしろその周囲のド・ブロイ波との相互作用を考えるべきである。
実際に 実験では 励起した原子から 円偏光もしくは直線偏光の電磁波が放射されるのを観察できる。
また 光の偉大な実験家 ラム ( ラムシフトの ) が 光子の粒子性に反対していた話は有名である。
また、最近の興味深い研究では、弱い測定によって、1光子が 電磁波(両スリットの)によって成り立っていることを示唆している。
(Science 2011, 332, 1170, S.Kocsis et al., Nature 2011, 474, 188, J.S.Lundeen et al.)
(Fig.13) 振動数 = 光子という粒子が振動している?
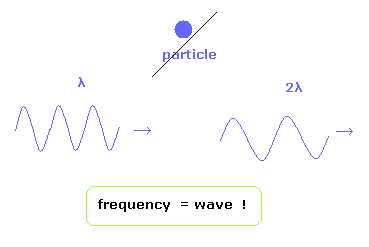
一般の教科書には 光電効果と波の振動数との関係が光子の粒子性の証明のように くどくどと書かれている。
まず第一に、振動数そのものの概念は電磁波という波の性質に基づくものであることはいうまでもない。
二つ目に、音波や波を生じる基になっている、空気や水を熱すると、それらの波を構成する各粒子の振動数は増加する。
つまり、エネルギーと振動数が密接に関係しあっていることは、しごくあたりまえの話なのである。
よって、光電効果はこのド・ブロイ波の量子化された状態の変化で説明可能である。
コンプトン効果では、もし 光が粒子だとしたら、その運動量が変化したとき、振動数のかわりに その速度 が変化するのが普通である。
上でも述べたように、振動数そのものは そもそも波の性質によることはいうまでもないことである。
(Fig.14) 便利な光子は ダークマター、エネルギー、ヒッグスなどで埋まった空間を素通りできる?
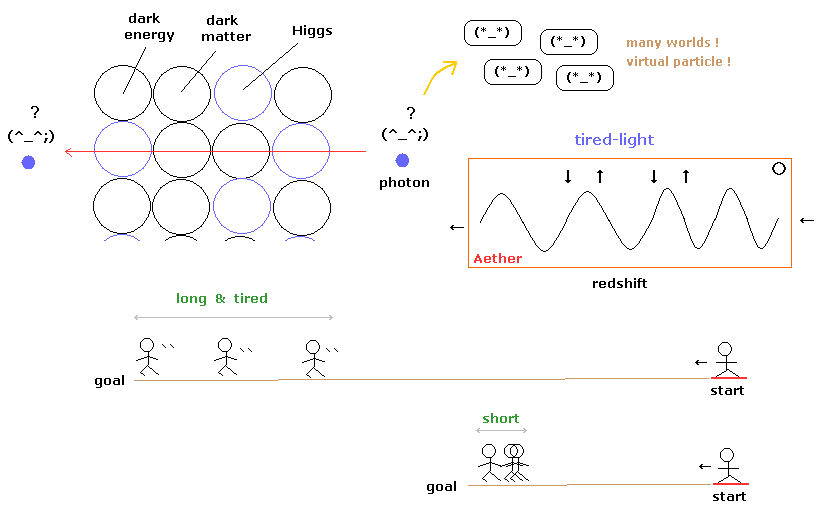
このページに示したように 光子という粒子は いろんな粒子で込み合った空間を 非常に長い期間進んでも まったく 無傷でいられる 特殊能力があることになる。
加速膨張宇宙による 赤方偏移は 空間を進むにつれて エネルギーが消失していくという "疲れた光理論" による解釈のほうが自然である。
超新星爆発からの 輝く光の期間は 遠くの星ほど長くなる。
これは マラソンランナー達と 100 メートルランナー達の 広がりの違いを思い浮かべれば容易に説明がつく。
また 光子の粒子性の概念は、 多世界解釈と 相対論に反する 仮想光子 (= クーロン力 ) を生み出す源となっている。( このページも参照のこと。 )
ここで, 光源が 宇宙空間に 電磁波もしくは光子を放出する場合を考える (Fig.15)。
(Fig.15)
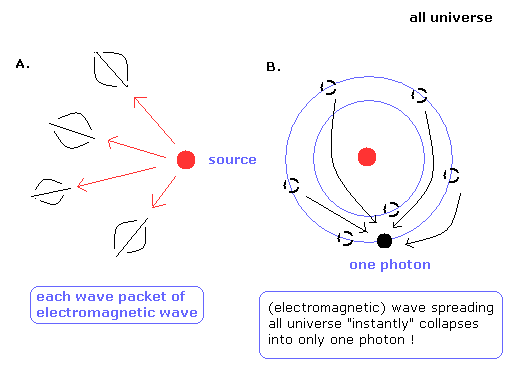
電磁波が 宇宙空間に どこまでも均等に広がり続けるという概念は 非常に不自然である。
光源から放出された電磁波は、多少は偏っていて、このことは より広い空間に広がったときに顕著になると考えるのが自然である。
それは、宇宙空間を 波束 (wave packet) として 進行することになる。(Fig.15A)
結果として、我々は 宇宙から届いた 電磁波の 各波束を検出することができる。
光子が粒子 である場合はどうなるだろう?
量子力学によれば、単一光子の 確率波 (= 電磁波)は 全宇宙空間に 無限に均等に拡大し続ける。
そして、ある地点で、この光子を検出したとき、全宇宙空間の電磁波が ”一瞬にして”たった1つの光子のもとに収縮してしまうのだ! (Fig.15B)
結論からして、この 光子のモデルはとうてい受け入れ難いものと言わざるを得ない。
一方、Fig15A の電磁波モデルは 非常に自然なモデルである。
光子とベルの不等式のページで述べたように、もし、一つの光子が分離できない粒子であるとしたら、エンタングルメントという奇妙な非局所的な現象は実際に起こっており、この現象を信じなければならない。
言いかえれば、もし、光子が分離可能な電磁波ならば、この光速以上の伝達を許すファンタジーを考慮する必要がないということだ。
どちらが(光子が粒子か波か)、より自然な話か、簡単に判断できることだろう
ボーア模型の水素原子では、基底状態の軌道は 次のように 1ド・ブロイ波長である。
(Eq.1)
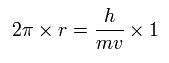
また、この軌道における 電子の 振動数 は 次のように 速度 / 軌道長 で表せる。 (Eq.1 を用いて。)
(Eq.2)
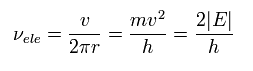
ここでは 次の関係式を使用している。
(Eq.3)
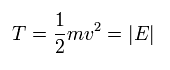
水素原子の円形軌道では、運動エネルギー (T) は 全エネルギー (E) の絶対値に等しい。
光電効果では, 次のエネルギーの光を水素原子に照射したとき、
(Eq.4)
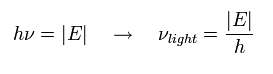
電子が水素原子から放出される。
電子の振動数 (Eq.2) は 光の振動数 (Eq.4) の ちょうど 2倍である。
電子の持つ運動エネルギーも光電効果に寄与することを考慮すれば、この結果は妥当と考えられる。
もし、電子の元の速度を保ったまま、放出させようとすると、必要な 光の振動数は次のようになる。
(Eq.5)
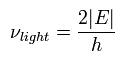
何と、Eq.5 は Eq.2 にちょうど等しくなるのである!
つまり、電磁波が 電子の運動を 振動させていることになる。(Eq.5 では それらの周期が同じである。)
Eq.2, Eq.4 (Eq.5) の結果は 光電効果の プランク定数 (h) は ド・ブロイ波に関係していることを意味している。
そのため、光電効果が 電磁波と ド・ブロイ波の相互作用によって生じると考えることは 非常に自然なことなのである。
電磁波による 光電効果に関しては、このページも参照のこと。
--------------------------------------
普通のマクスウェルの方程式を解くと、次の関係式が得られる。
(Eq. M-1)
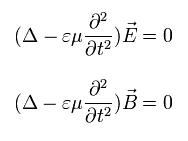
ここでは、次の関係式が満たされる。
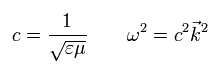
上の式から ”自然に”電磁波の解を得ることができる。(Eq.6)
例えば z 方向へ進む 電磁波は 次の変動する電場と磁場より構成される。
(Eq.6)
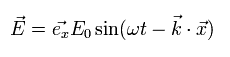
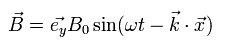
Eq.6 は 上の Eq.M-1 の式の 解 である。
Eq.6 に示すように、本来の 電磁波における E と B の振幅は 減衰しないで進行する。
しかし、加速度運動する電荷に対する 古い式によれば、電磁波の振幅が次のように減衰してしまう。
(Eq. M-2)

ここでは、p は 電気双極子を意味している。
Eq M-2 では、加速度運動する 電気双極子が 電磁波を放出することを示している。
また、この双極子と 観測地点の距離 (= r) が長くなるほど、E と B の振幅は Eq.M-2 に示すように 弱くなる。
どうして、Eq.M-2 の結果は Eq.6 と異なるのだろうか?
重要な点は、Eq.M-2 は ド・ブロイ波の概念をまったく使用していないことである。
すべての運動する粒子は ド・ブロイ波を生じるにも関わらず、どうして Eq.M-2 は このことを無視しているのだろうか?
これが、我々が 電磁波について誤解している原因である。
特に、原子などにおいては、我々は 量子化されたド・ブロイ波を考慮しなければならない。
もしそうすると、電磁波(束)の発生方向に偏りが存在し、Eq.6 に示すように減衰されないことになる。
古いマクスウェル方程式のみの概念によれば、電磁波の エネルギー密度 (u) は次のように表される。
(Eq.7)
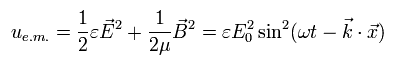
しかし、Eq.7 のエネルギー密度の式はある欠陥を含んでいる。
Eq.7 によれば、角振動数 (ω) が まったく エネルギーに貢献していないのである。(原子レベルにおいて。)
Eq.7 の角振動数を次のように変化させても、全エネルギーはまったく変化しないのである。
(Eq.8)
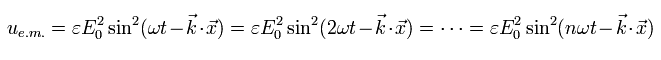
[ これらの電磁波のエネルギーは本当に同じなのか? ]
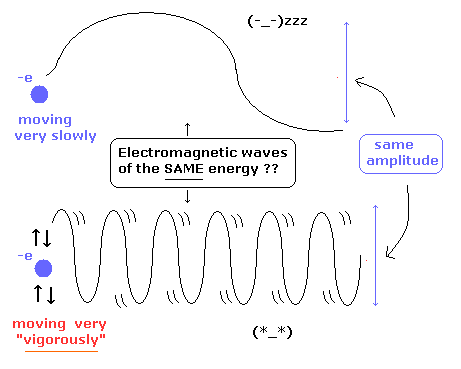
ここでは、上の電子は ゆっくりと上下に揺れている。一方 下の電子は 非常に激しく振動している。
また、これらの 振幅は同じ である。
Eq.8 の解釈によれば、これらの電磁波のエネルギーが 何とまったく同じになるとしている。
これは 非常に不合理 と言わざるを得ない。
つまり、Eq.8 のエネルギー密度の式は 不完全なものなのである。
そのため、我々は 光電効果に対する 古い概念を改めなければならない。
基本的に 振動数なるものは、波の性質によるものである。(粒子のよるものでない。)
このことは しごくあたりまえの話である。
もし 電磁波に 振動数 を組み合わせれば、 我々は 光子という概念をまったく使用する必要がないのである。

2010/2/15 updated This site is link free.