(Eq.1)
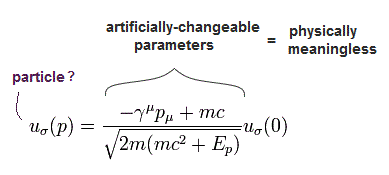
And
(Eq.2)
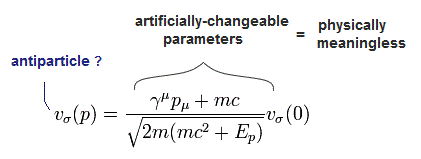
where
(Eq.3)
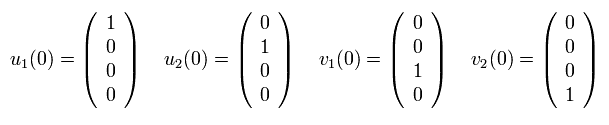
Top page (correct Bohr model including the two-electron atoms)
Strange "spin" is NOT a real thing
What are "real" elementary particles ?
First we explain about "left-handed" and "right-handed" spinors.
Can we visualize these states ??
As shown in this page, u(p) and v(p ) of Dirac's spinors are
(Eq.1)
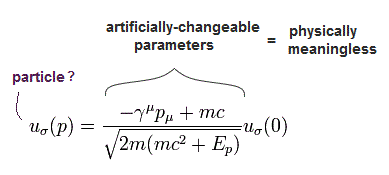
And
(Eq.2)
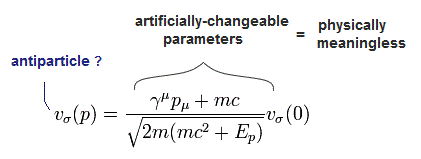
where
(Eq.3)
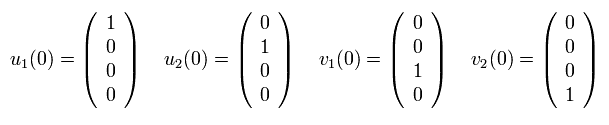
Here we use Pauli matrices of
(Eq.4)
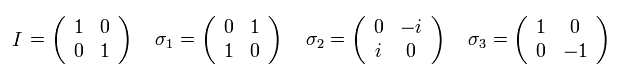
And γ matrices are
(Eq.5)
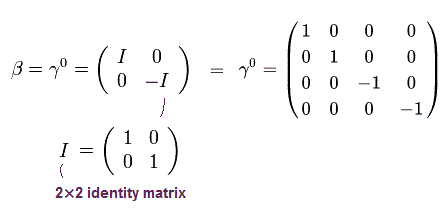
(Eq.6)
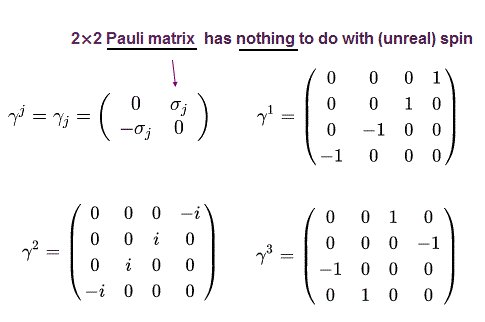
From Eq.3, Eq,4, Eq.5 and Eq.6, the numerator of Eq.1 (of u1(p) ) is
(Eq.7)
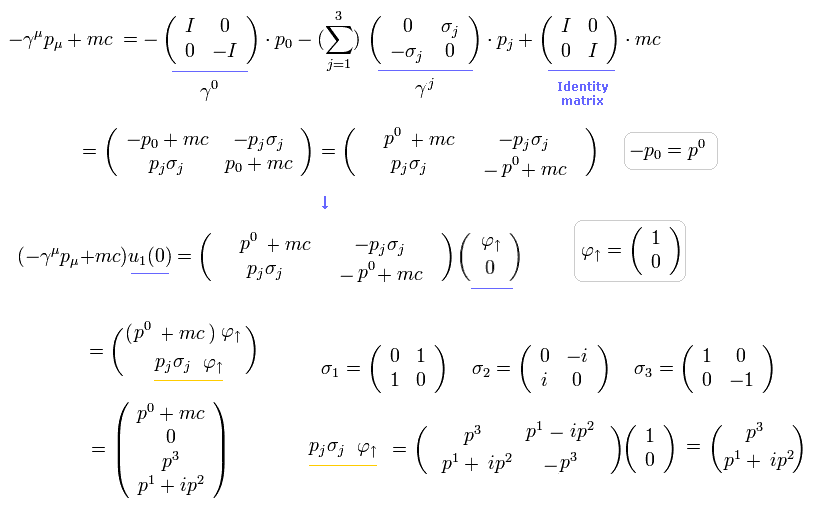
where we use (-1, +1, +1, +1) version.
So u1(p) of Eq.1 is
(Eq.8)
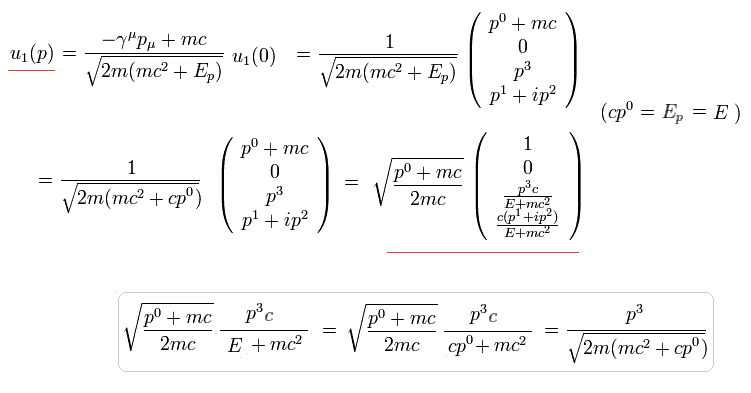
In the same way, u2(p) of Eq.1 is
(Eq.9)

v1(p) of Eq.1 is
(Eq.10)
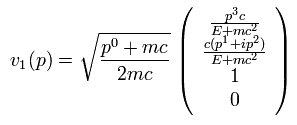
v2(p) of Eq.1 is
(Eq.11)
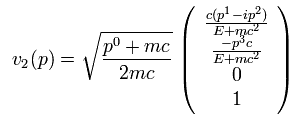
Here we use the γ matrix of
(Eq.12)
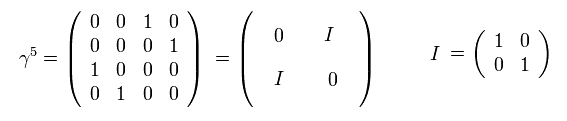
When this γ5 acts on u1(p),
(Eq.13)

When the mass m is zero, and the particle moves in the z direction,
(Eq.14)

Substituting Eq.14 into the last line of Eq.13, and paying attention to σ3
(Eq.15)
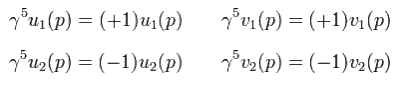
From Eq.15,
(Eq.16)
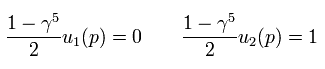
If we define
(Eq.17)
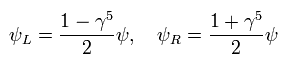
The wavefunction can be divided like
(Eq.18)
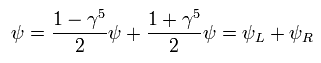
Using the relations of
(Eq.19)
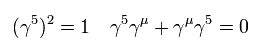
and
(Eq.20)
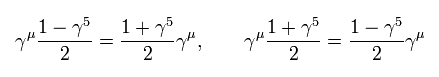
Dirac equation is
(Eq.21)
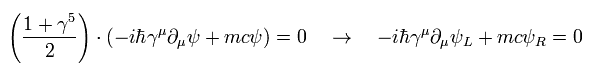
Eq.21 means when the mass of fermion is zero, only left-handed (or right-handed ) particle is left.
(When the fermions get mass, the left-handed and right-handed particles are mixed, they say. )
But unfortunately, we can not visualize these left-handed (or right-handed ) states.
To get a cross section in QED. we need to calculate the probability amplitude in Feynman diagram.
First I advise you these are very "mathematical" than physical.
In this web page we use the notations and relations of this page and this page.
(Ap.1)

The wavepacket representing some state can be expressed as
(Eq.22)
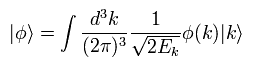
where the sum of all probabilities adds up to 1,
(Eq.23)
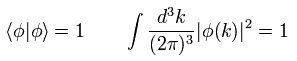
where we use the relations and | k > of Ap.1.
The probability (= a square of amplitude ) of the transition ( A+B → 1+2 ) is
(Eq.24)
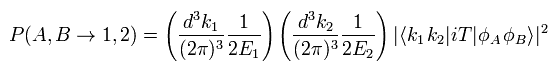
where iT includes the interaction term of S-matrix.
S-matrix is an unitary operator, which causes transition during some time.
So, we can define
(Eq.25)
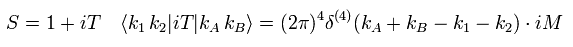
The delta functions of energy and momentum conservation are always included in Eq.25.
(This is calculated later.)
(Fig.1)
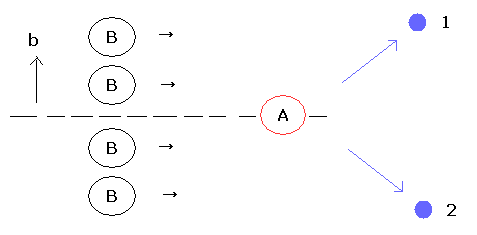
As shown in Fig.1, the wavepacket of B is supposed to be uniformly distributed in impact parameter b (= two dimensional plane).
So the number of scattering event (N) and the cross section (σ) are
(Eq.26)
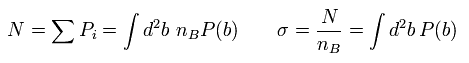
where we integrate by b in some plane.
And nB means the number density of B.
Using Eq.22, Eq.24, Eq.25, and Eq.26, the (differential) cross section is
(Eq.27)
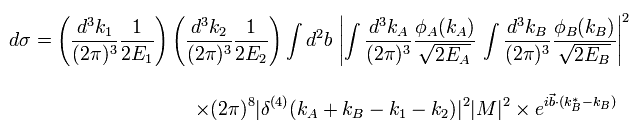
where exponential function of b means de Broglie's waves (= probability amplitude ) of b.
Eq.27 includes six momentum integration of A ( or B ) ( 3 × dkA, and 3 × dkA* ).
First we integrate, as follows,
(Eq.28)
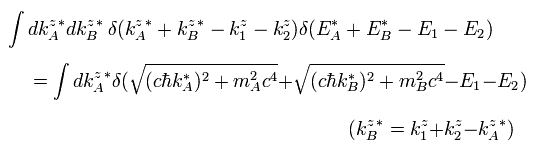
Here we use the next formula of delta function.
(Eq.29)
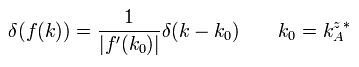
When f(k) is
(Eq.30)
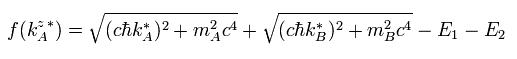
f '(k) becomes
(Eq.31)
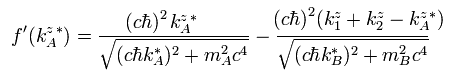
As a result, if we consider E = mc2 approximately and use Eq.29 and Eq.31, Eq.28 becomes
(Eq.32)
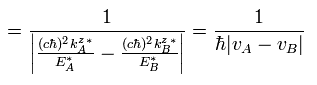
where velocity v = p/m, and the momentum p = ħ k.
Next in Eq.27, we do the integration of
(Eq.33)
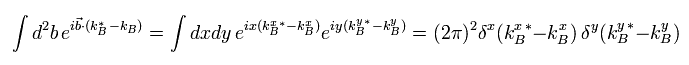
And we do the next integration using the results of Eq.33.
(Eq.34)
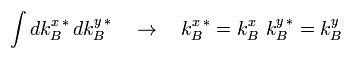
And in Eq.27, we do the next integrations of
(Eq.35)
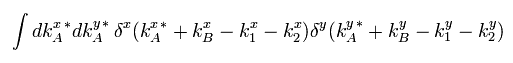
From Eq.32, Eq.33, Eq.34, and Eq.35, Eq.27 becomes
(Eq.36)
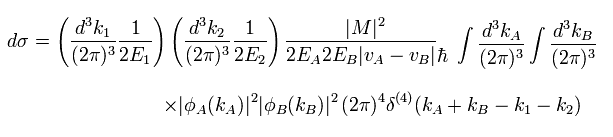
Considering Eq.23, Eq.36 becomes
(Eq.37)
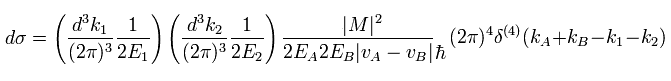
And then we integrate by momentum (wave number k) of the final state 2, as follows,
(Eq.38)
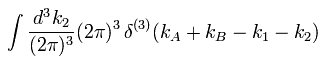
The integration of dk3 of the final state 1 can be expressed using a solid angle, as follows,
(Eq.39)
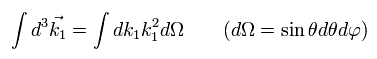
Using the formula of Eq.29,
(Eq.40)
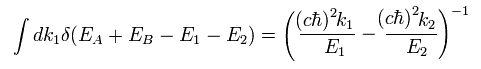
Here we suppose the center of mass frame,
(Eq.41)
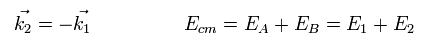
where Ecm is the total energy.
From Eq.41, Eq.40 becomes
(Eq.42)
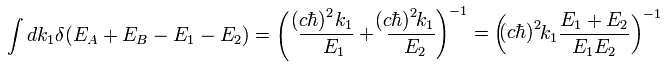
From Eq,38, Eq.39, Eq.40, and Eq.42, Eq.37 becomes
(Eq.43)
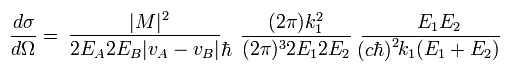
Using Eq.41,
(Eq.44)
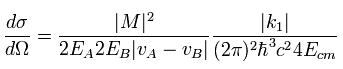
Using the approximation of
(Eq.45)
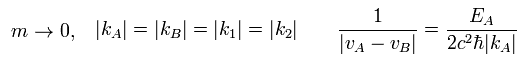
where | vA - vB | is 2c, approximately.
Using Eq.45, Eq.44 is
(Eq.46)
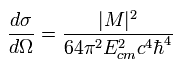
This is the differential cross section in relation to a solid angle.
Here we confirm the dimention of Eq.46 is a square of meter.
Basically, the dimension of Dirac delta function is a reciprocal of the number in it, as follows,
(Eq.47)
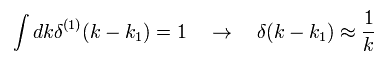
The dimensions of the wave number (k), energy (E), light speed (c), and Planck constant (h) are
(Eq.48)
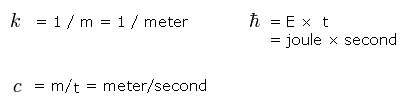
So the dimension of M of Eq.25 is
(Eq.49)
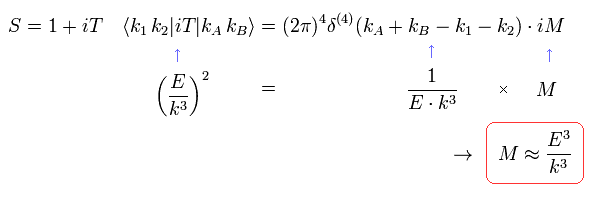
where the exponential function of S matrix has no dimension.
And from Ap.1, one pair of |k> is the dimension of E/k3.
So the dimension of Eq.46 is
(Eq.50)
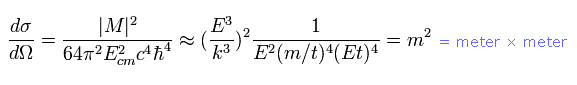
As a result, the dimension of differential cross section is a square of meter.
Next we calculate the amplitude of the most important reaction of QED.
(Fig.2)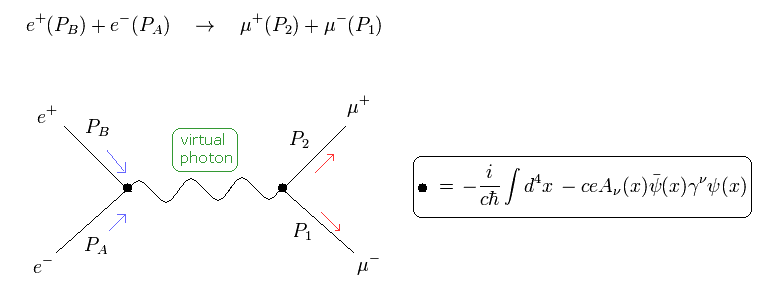
In Fig.2, the high energy electron (e-) and positron (e+) crash into each other and changes into virtual photon.
And then the virtual photon (= photon propagator) changes into muon (μ-) and antimuon(μ+).
This calculation process applies to the generation of quark and antiquark, too.
Of course, these final products are unstable, so they changes into the stable electron, γ rays, and neutrino soon.
About Feynman diagram and concrete calculation methods, see also this page.
Here we suppose the momentums of the initial electron and positron are PA and PB.
(So their wave numbers are kA and kB.)
And the momentums of the final products muon and antimuon are P1 and P2.
Using Dirac wavefunction of
(Eq.51)
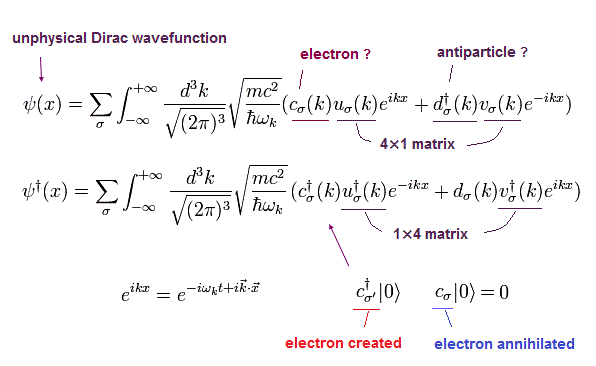
And its conjugate transpose (× γ0) is
(Eq.52)
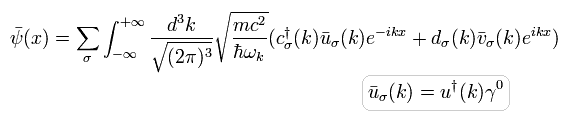
And the photon propagator of
(Eq.53)
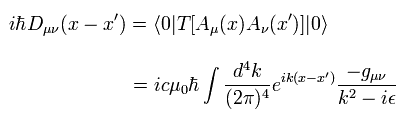
The probability amplitude of Fig.2 is
(Eq.54)
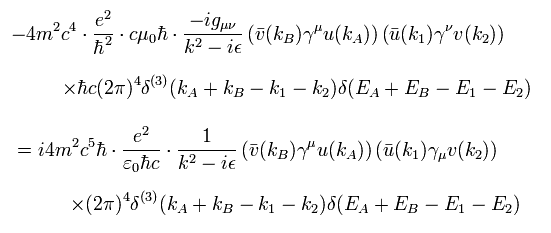
where we use < k | and | k > of Ap.1.
From Eq.25, M is
(Eq.55)
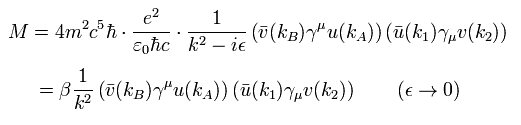
And a squared matrix element is
(Eq.56)
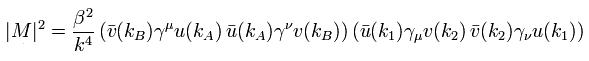
Using the trace technique of Eq.49-Eq.51 of this page. Eq.56 is
(Eq.57)
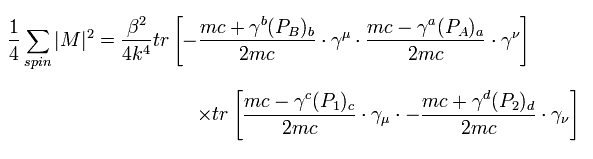
where we use the relations of u and v in Ap.1.
And the final states can take all spin states, but the inital states can take one of up and down spins.
So 1/2 × 1/2 = 1/4 is added. (Though this is a little difficult to imagine.)
From Eq.55, Eq.57 is
(Eq.58)
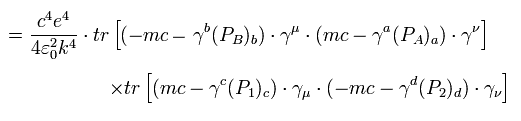
Here we use the next trace formulas of gamma matrices.
(Eq.59)
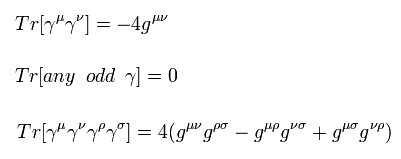
This homepage uses (-1, 1, 1, 1) version metric tensor.
The trace of odd γ matrices is zero, so
(Eq.60)
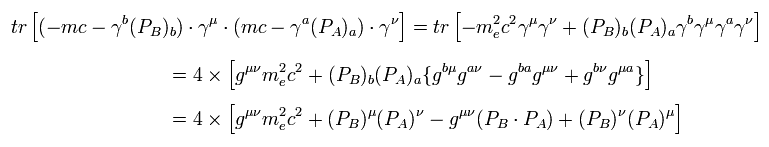
In the similar way,
(Eq.61)
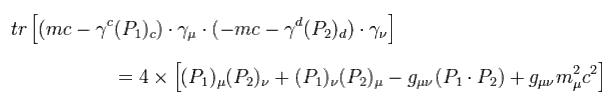
Here the mass of the electron is supposed to be zero ( me = 0 ), and do the calculations such as
(Eq.62)
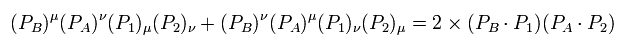
and
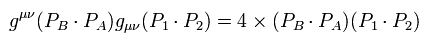
and
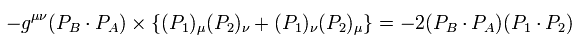
We can get
(Eq.63)
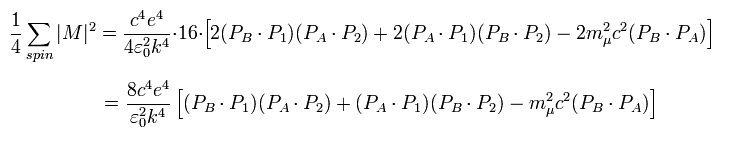
Here the momentums and energies of the electron (A) and positron (B) are supposed to be
(Eq.64)
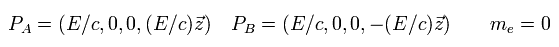
And those of muon (1) and antimuon (2) is
(Eq.65)
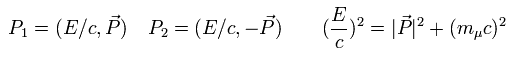
where the angle between momentum of muon and z axis is θ, as follows,
(Eq.66)
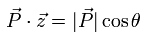
The momentum and energy of the virtual photon is the sum of the electron and positron, so from Eq.64,
(Eq.67)
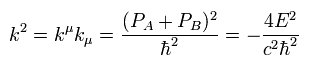
where k is the wave number of photon.
From Eq.64 to Eq.66
(Eq.68)
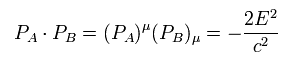
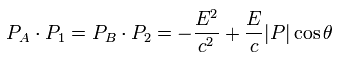
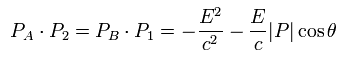
Using Eq.67 and Eq.68, Eq.63 is
(Eq.69)
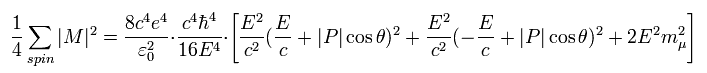
Here we define
(Eq.70)
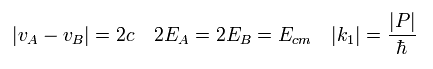
Using Eq.70, Eq.44 is
(Eq.71)
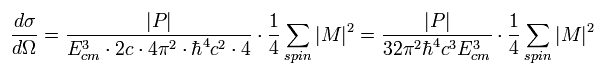
Substituting Eq.69 into Eq.71
(Eq.72)
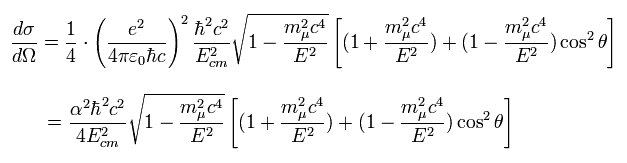
where we use the fine structure constant α
This is a little complicated.
But the important point is that the cross section is proportial to each charge, which can be said also in Rutherford scattering.
As you see in the trace of γ matrices, these are only "mathematical" things. ( NOT physical objects at all.)

2011/12/25 updated. Feel free to link to this site.