
Top page (correct Bohr model, and quantum mechanics is wrong )
Strange "spin" is NOT a real thing.
What is real elementary particles ?
Quantum electrodynamics (= QED ) is an useless meaningless theory.
This web page uses the ( -1, +1, +1, +1 ) version of the relativistic four-vector, as shown in the appendix.
And the next relations are used in this homepage.
(Ap. 1) This web page.

LI means the interaction Lagrangian ( q = charge, A = vector or scalar potential, φ = Dirac's wavefunction ).
And c(k) and c†(k) means the particle's annihilation and creation operators.
u(k) and v(k) mean Dirac's spinors ( see this page).
The last line is the notation of the particle's creation (its wave number k ) from the vacuum.
Some other textbooks uses the next notations instead of Ap.1.
(Ap. 2) Other textbooks.

The light green areas are different parts in Ap.1 and Ap.2.
But the anticommutation relations of Dirac's wavefunctions are the same in Ap.1 and Ap.2 (canceling their different parts).
Change notations when you need based on these relations.
Ratherford scattering was explained by Rutherford in 1911 using the planetary models such as Bohr model.
He considered the gold nucleus and alpha particle as point particles, and thought the repulsive Coloumb force caused the scattering of the alpha particle.
As the two particles become closer to each other, the Coulomb interaction (repulsive or attractive) between them becomes stronger.
As a result, the alpha particle is deflected by large angle ( over 90 degrees ).
If the target nucleus is not a point particle, the scattering pattern becomes different from the Coloum interaction pattern.
The result showed that the gold nucleus was like a point particle.
He used the classical-mechanical method.
First, we derive the Rutherford scattering cross section by the classical method.
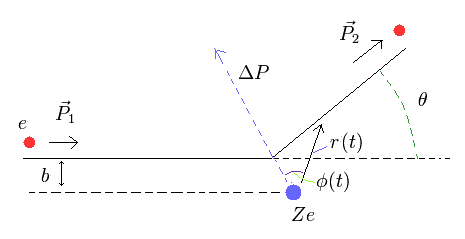
Fig.1 Rutherford ( Coulomb ) scattering model.
The differential cross section is equal to the area of the ring, as follows,
(Eq.1)
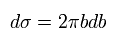
From Eq.1,
(Eq.2)
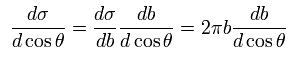
Here the magnitude of the the particle's momentum doesn't change after scattering.
So only its direction changes (= elastic scattering ).
(Eq.3)
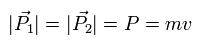
where m is the particle's mass and v is the velocity.
When the angle between the particle's momentums before (= P1 ) and after (= P2) scattering is θ, the change of the momentum is
(Eq.4)
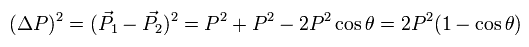
changing cosθ into 1 - 2 sin2 (θ/2),
(Eq.5)
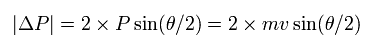
The change of the momentum is equal to the impulse (= Ft ) the particle receives in the whole scattering process, as follows,
(Eq.6)
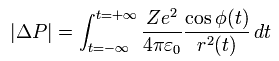
Here the force is Coloumb force between the two charges ( e and Ze ), and φ(t) is the angle between the directions of the impulse and r(t) (= position vector ).
In the Coulomb interaction between them, the angular momentum (L) is conserved.
As shown in Fig.1, the first angular momentum is mv × b.
(Eq.7)
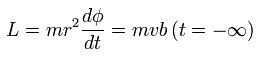
From Eq.7,
(Eq.8)
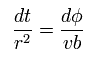
From Eq.6 and Eq.8,
(Eq.9)
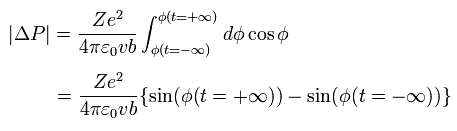
Here,
(Eq.10)
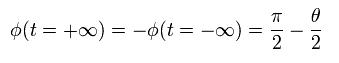
Substituting Eq.10 into Eq.9,
(Eq.11)
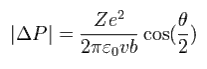
From Eq.5 and Eq.11,
(Eq.12)
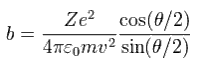
From Eq.12,
(Eq.13)
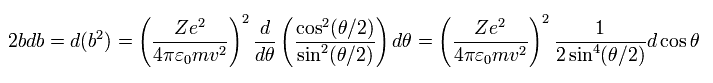
where we use the relation of
(Eq.14)
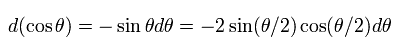
Using the solid angle (Ω), the differential cross section ( Rutherford scattering formula ) is
(Eq.15)
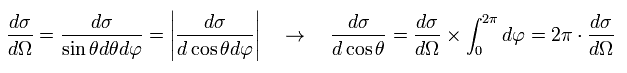
From Eq.1, Eq.13, and Eq.15,
(Eq.16)
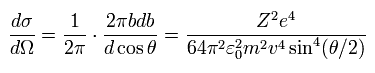
Eq.16 is the famous Rutherford scattering formula (by the classical method).
Next we try to derive Rutherford scattering formula by QED method.
Dirac equation of QED includes relativistic and spin effects.
When we consider the relativistic effect, it is called Mott scattering.
Unfortunately, from QED method we can not imagine the real world. It's only a "mathematical" language.
(You need to remember this fact.)
Also in QED, we use the classical Coulomb relation. So the scalar potential ( A0 = φ/c ) is
(Eq.17)
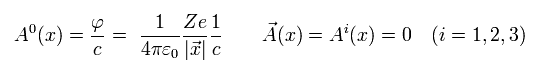
where we suppose the static electric field, so the vector potential (= Ai ) is zero.
From Ap.1 and Eq.17, the interaction Lagrangian between photon and fermion is
(Eq.18)
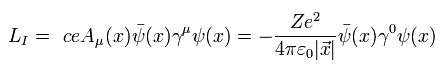
where we use (-1, 1, 1, 1) version.
The number (N) of the particle ( charge = e ) scattering during the long time T is
(Eq.19)
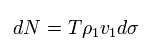
where ρ1 is the particle's number density, v1 is its velocity, and dσ is differential cross section.
Approximately, the velocity v1 is
(Eq.20)
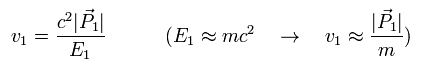
In QED, the number of the scattering events into some infinitesimal momentum space (= d3P2 ) is expressed as
(Eq.21)
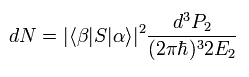
where α and β are initial and final states of the Coulomb scattering, and S means S matrix.
E and 2πħ are needed for normalization.
S matrix can be expressed as unitary operator of interaction Hamiltonian, as follows,
(Eq.22)
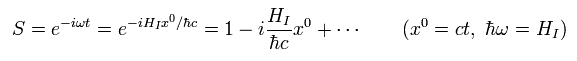
As shown in Ap.1, this homepage expresses the initial state with wave number (k1), as follows,
(Eq.23)
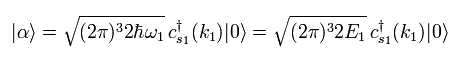
These coefficients are cenceled out by the normalization factor of Eq.21.
And the final state can be expressed using annihilation operator, as follows,
(Eq.24)
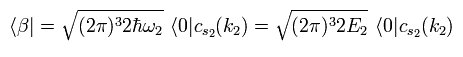
Here the initial and final states are supposed to have the same energy.
So the nomalization factor of Eq.21 can be expressed as
(Eq.25)
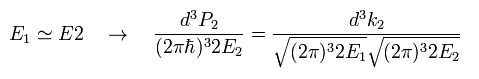
And the number density (= ρ1 ) of the particle is supposed to be
(Eq.26)
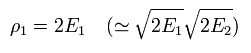
In fact, this ρ1 value can be manipulated artificially.
This energy dimension is introduced to make cross section's dimension a square of meters.
Considering Lorentz contraction, the ratio of density to relativistic energy becomes Lorentz invariant, as follows,
(Eq.27)
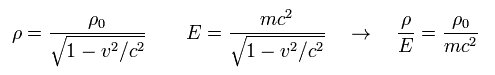
So for example, we can change Eq.26 into the next value to keep Lorentz-invariant.
(Eq.28)
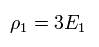
From Eq.19, Eq.20, Eq.21, and Eq.26, the differential cross section is
(Eq.29)
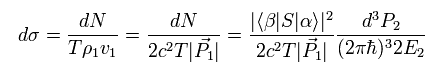
The total energy is conserved, so we can express the probability amplitude of the translation, as follows,
(Eq.30)
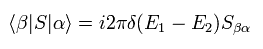
Dirac's delta function can be expressed as follows,
(Eq.31)
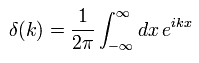
Using Eq.31, the next equation can be gotten.
(Eq.32)
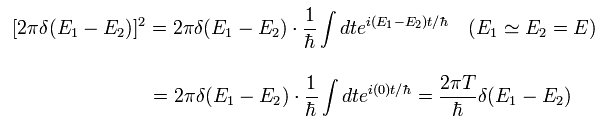
And the infinitesimal momentum space of Eq.29 can be expressed using a solid angle, as follows,
(Eq.33)
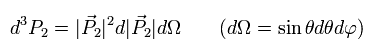
According to Einstein relativistic formula,
(Eq.34)
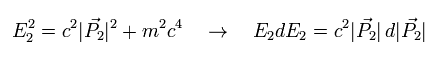
From Eq.33 and Eq.34,
(Eq.35)
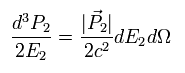
From Eq.29, Eq.30, Eq.32, and Eq.35,
(Eq.36)
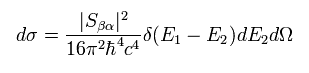
where we use |P1| = |P2|.
Integrating Eq.36 by E2,
(Eq.37)
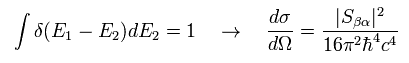
In S matrix of Eq.22, we consider only first-order interaction effect.
From E.18 and Eq.22,
(Eq.38)
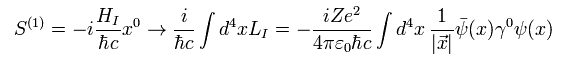
where LI means Lagrangian density, so we integrate it in all space (+ all time ).
Here we use the next Dirac's wavefunctions.
(Eq.39)
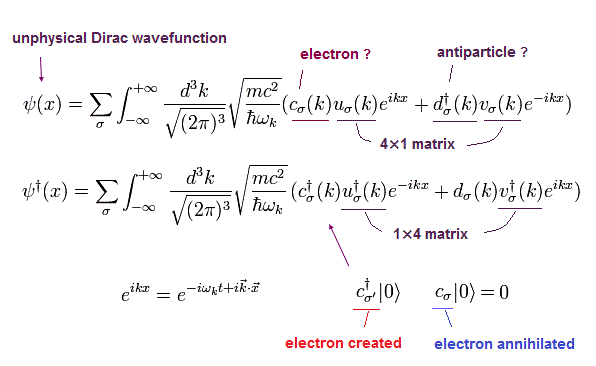
And its conjugate transpose (× γ0) is
(Eq.40)
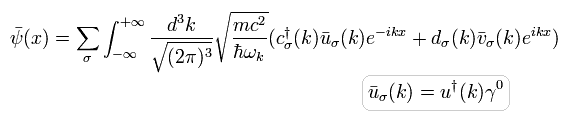
Substituting Dirac's wavefunctions ( Eq.39, Eq.40 ) into Eq.38, and using in and out states ( Eq.23 and Eq.24 ),
(Eq.41)
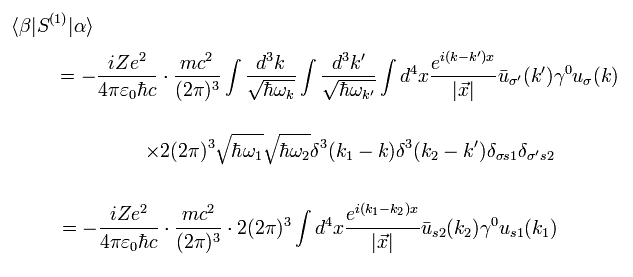
where we use the anticommutation relation of Ap.1
Here we use the formula of
(Eq.42)
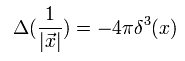
We can prove Eq.42 by Gauss's law, as follows,
(Eq.43)
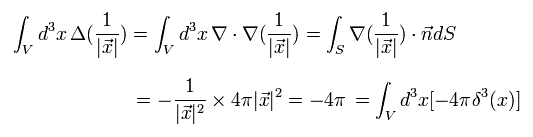
Using Eq.42,
(Eq.44)
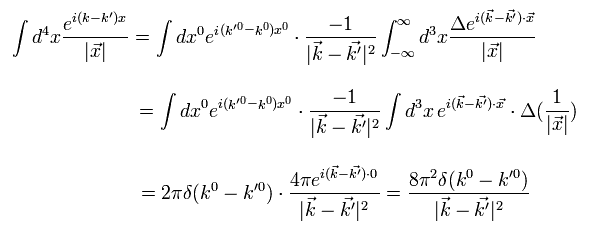
We do partial integration twice in the second line.
Substituting Eq.44 into Eq.41,
(Eq.45)
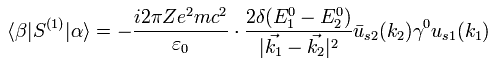
where we use the relation of
(Eq.46)
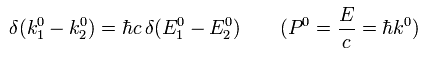
From Eq.30 and Eq.45,
(Eq.47)
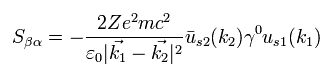
Substituting Eq.47 into Eq.37,
(Eq.48)
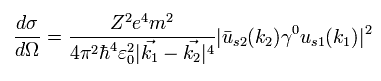
As shown on this page, we can use the trace technique of
(Eq.49)
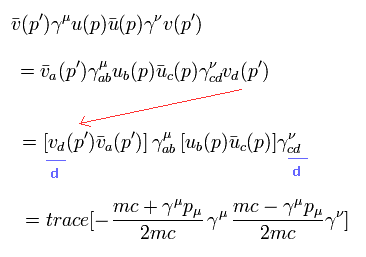
(Eq.50)
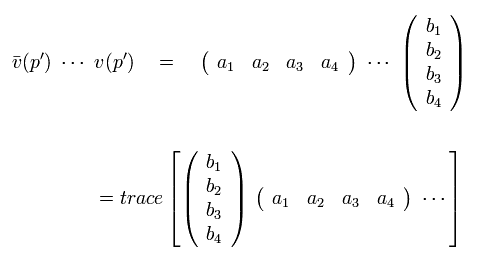
Using Ap.1,
(Eq.51)
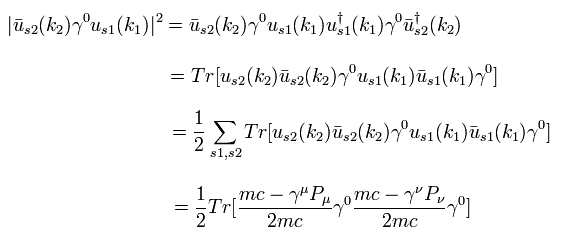
where we use
(Eq.52)
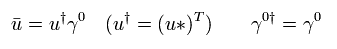
And after summing all spin states, we divide it by two, because only the initial state is in one of two spin states.
( This may be difficult to imagine. But this is necessary to get correct results. )
Here we use the next trace formulas of gamma matrices.
(Eq.53)
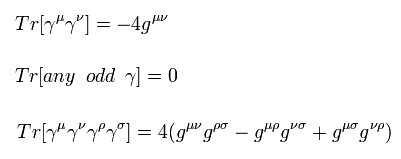
This homepage uses (-1, 1, 1, 1) version metric tensor.
The important point is that traces of any odd gamma matrices become zero.
Using Eq.53, the remaining terms of Eq.51 are
(Eq.54)
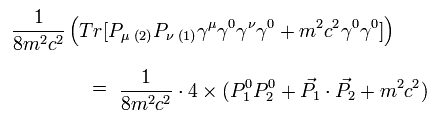
where we sum all μ and ν.
When the angle between the momentum vectors P1 and P2 is θ,
(Eq.55)
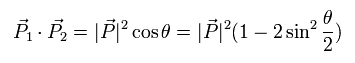
Substituting Eq.54 and Eq.55 into Eq.48,
(Eq.56)
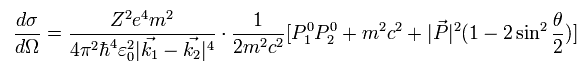
From Einstein's relativistic equation,
(Eq.57)
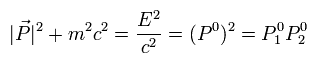
Like the classical case of Eq.5,
(Eq.58)
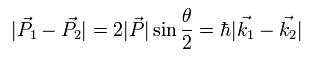
Substituting Eq.57 and Eq.58 into Eq.56,
(Eq.59)
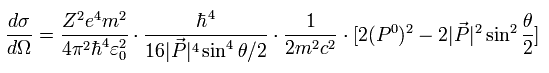
where we use the next relation of
(Eq.60)
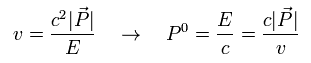
Substituting Eq.60 into Eq.59, we can get the formula of relativistic Mott scattering of
(Eq.61)
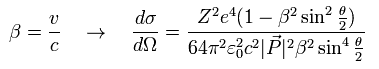
Eq.61 is said to include "relativity" and "spin" effect (= γ matrices ).
But unfortunately, we can not imagine any concrete images from this "abstract" calculation process.
Can you imagine any images from matrices ??
And there are several parts we can manipulate in this process.
According to the relativistic effect, as the particles becomes faster, it is more difficult to accelerate the heavier particle.
But as shown on this page, we can explain this relativistic mass effect by the electric "aether" theory naturally.
When β of Eq.61 is close to zero (= nonrelativistic approximation ), and substituting |P| by mv,
(Eq.62)
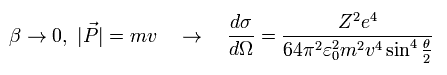
We can get the classical Rutherford formula of Eq.16.

2011/12/24 updated. Feel free to link to this site.