Top page (correct Bohr model including the two-electron atoms)
Schrodinger equation is a wrong version of Bohr Sommerfeld model !
Electron spin is an illusion !
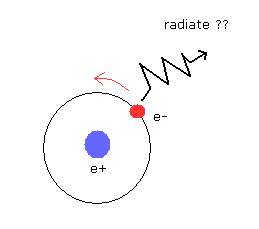
The quantum mechanical textbooks often says that Bohr's classical orbit is incorrect, because its electron is going around the nucleus and radiates electromagnetic waves (= energies) due to the "accelerated" charge.
(Fig.1) Bohr's electon really radiates energy ?

But actually, almost all real charged particles on the earth are "accelerated", and stable.
( It is impossible that all charged particles in this real world are always still. )
And as shown in this page, considering the reduced mass and the relativistic effect in atoms, the electron and the nucleus are actually moving (and accelerated ).
(Hydrogen energy levels and reduced mass)
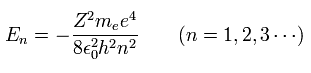
where we have to replace it by the reduced mass (μ) to get the correct energy values.
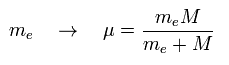
which means that the nucleus and electron of the hydrogen are actually moving around the the center of mass.
So in Bohr's orbit, an integer times de Broglie wavelength makes the orbit stable.
( If we don't think about the de Broglie wave, the ground state energy of the hydrogen can be much lower than the experimental value. )
By the way, the classical Maxwell's laws really showed that the accelerating charges radiate energy ?
In fact, there were some mistakes in it.
At that time, his theory didn't think about the quantization of the charge (= -e or + e), which caused the wrong classical vacuum energy.
(Of course, Maxwell's theory itself is a very great theory and valid now.)
(M-1) Poynting vector = energy flow ??
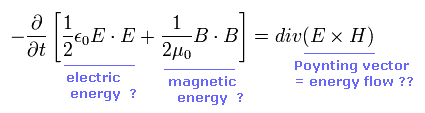
To insist that an accelerated electron radiates energy, Poynting vector (= E × H ) needs to mean an energy flow.
For the Poynting vector to be an energy flow, the vacuum electric energy and magnetic energy MUST be "real" energies.
(M-2) A single electron -e = -dq -dq -dq -dq ...?
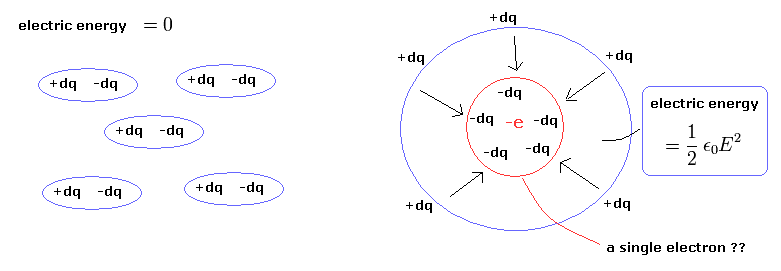
As shown in M-2, the vacuum electric energy (= M-1) of Maxwell's world means the potential energies among infinite small charges (= -dq ) included in a single electron spherical conductor.
But of course, a single electron is NOT made from smaller charges than -e, and it can NOT be broken into pieces.
So in case of a single electron (or proton ), the vacuum electric energy is meaningless, which means Poynting vector is meaningless, too.
( As I say later, the magnetic energy (= current i × induced voltage ) is also meaningless in a single electron. )
(M-3) Poynting vector is NOT an electromagnetic wave.
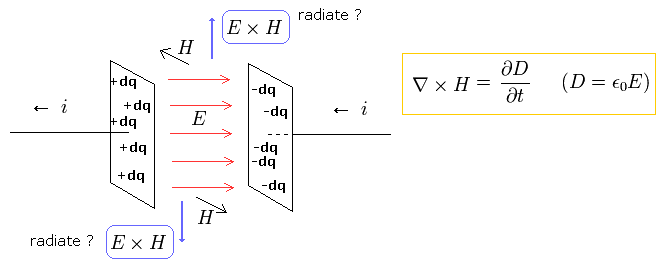
The important point is that the electric and magnetic energies of M-1 are only indicators, and NOT energies themselves.
"Real" energies are stored in electric "conductors", capacitor "plates", or solenoid's "wires", NOT in the vacuum.
For example, in a capacitor of M-3, the potential energies among the small charges (= dq ) in the plates are "real" energies.
In M-3, the electric current i is reducing the stored charges ( and electric field E ), which causes the magnetic field H around them.
According to the definition of Poynting vector (= E × H ), the M-3 capacitor radiates energy in the direction of the Poynting vector ?
Answer is NO. these energies are transmitted through the wire to other things such as solenoids ( NOT through the electromagnetic waves ). See also Fig.7.
So the Poynting vector is only a indicator, and NOT a "real" energy flow.
Of course, in a single electron, Poynting vector is neither a indicator nor a real energy flow.
Considering the light speed c of the electric (or magnetic) field propagation, the retarded scalar potential (= φ) and the
vector potential (= A ) are
(Eq.1)
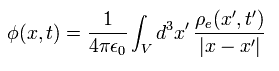
where ρe means charge density.
(Eq.2)
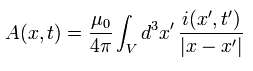
where i means current density.
here,
(Eq.3)
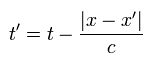
So when we observe some electric potential on the point x at the time t, it means that its potential was emitted from the point x' at the time t'.
(Fig.2)

As shown in Fig.2, the distance R is approximately,
(Eq.4)
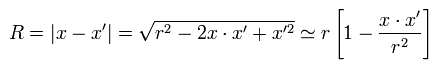
where the point x is very far away from the origin 0 (= charged area ), as follows,
(Eq.5)
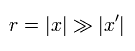
So 1/R is
(Eq.6)
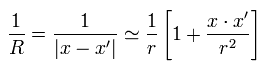
Using Eq.4, the carge density ρe on the point x' is expressed as
(Eq.7)
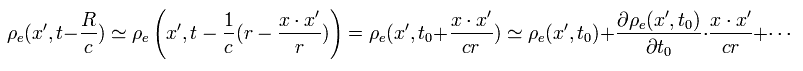
where
(Eq.8)
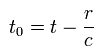
Substituting Eq.6 and Eq.7 into Eq.1 and leaving the first degree effect of x', the energy potential is
(Eq.9)
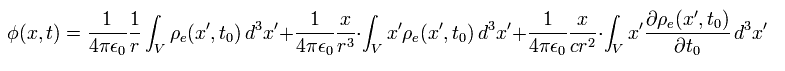
The integral part in the first term of Eq.9 means the total charge (= Q ) in the region V.
And that in the second term means the electric dipole moment (= p(t) ), as follows,
(Eq.10)
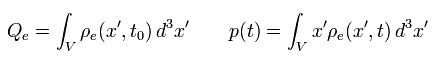
And the integral part of the third term of Eq.9 is
(Eq.11)
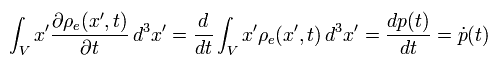
Using Eq.10 and Eq.11, Eq.9 becomes
(Eq.12)
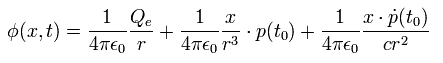
(Caution: x of Eq.12 doesn't mean the coordinate x of (x, y, z) but the vector.)
If we replace R by r approximately in Eq.2, the vector potential A becomes
(Eq.13)
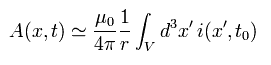
Due to the conservation of the charge, Eq.11 is expressed as
(Eq.14)
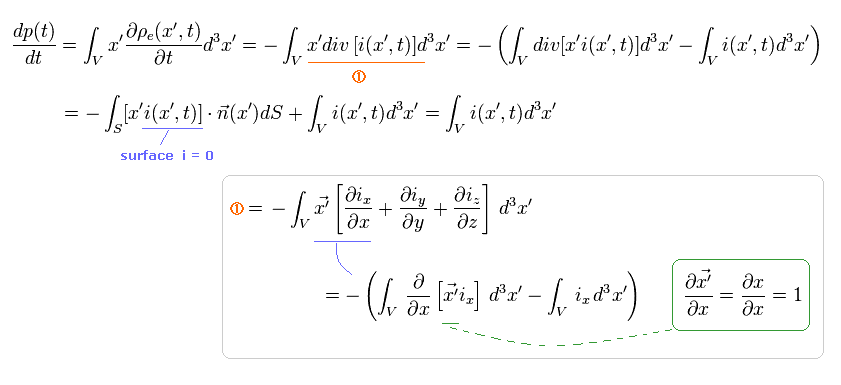
where the current i on the surface area S is supposed to be zero (= perpendicular to n vector ).
From Eq.14, Eq.13 is
(Eq.15)
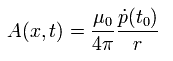
Next we try to get the electric field E by differentiating Eq.12.
(The first term of Eq.12 is the static field, so we don't need to consider it.)
Differentiating the second term of Eq.12 with respect to x (= x component of (x, y, z) ),
(Eq.16)
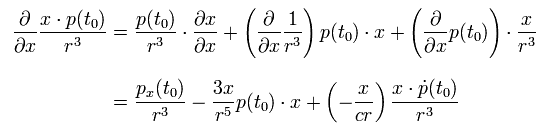
where we use
(Eq.17)
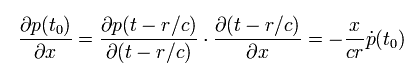
As a result, the gradient of the second term of Eq.12 is
(Eq.18)
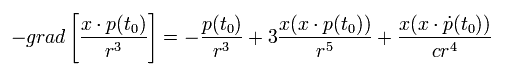
( x of Eq.18 doesn't mean x component of (x, y, z) but the vector. )
In the same way, differentiating the third term of Eq.12 with respect to x (= x component of (x, y, z) ),
(Eq.19)
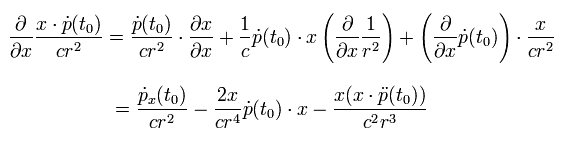
where we use Eq.17.
So the gradient of the third term of Eq.12 is
(Eq.20)
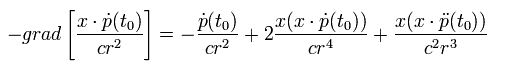
From Eq.15, Eq.18, and Eq.20, the electric field E at the point x is
(Eq.21)
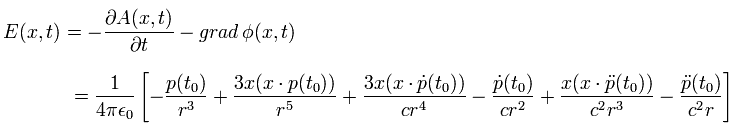
where we use
(Eq.22)
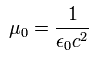
And from Eq.15 and Eq.17, the magnetic field B (= x component) is
(Eq.23)
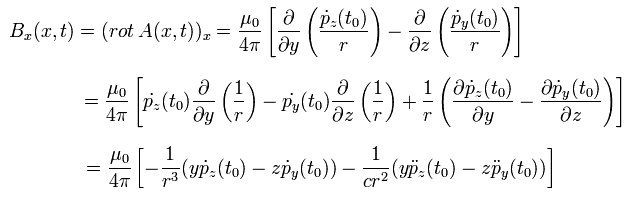
So the magnetic field B is
(Eq.24)
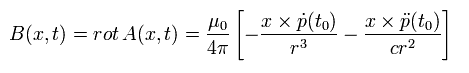
From Eq. 21, the changing electric fields E including the first (= E1 ) or second (= E2 ) derivatives of the electric dipole are
(Eq.25)
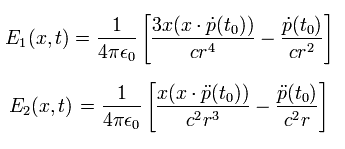
From Eq. 24, the magnetic fields B including the first (= B1 ) or second (= B2 ) derivatives of the electric dipole are
(Eq.26)
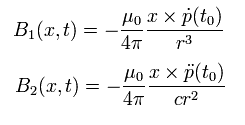
Here we define the unit vector er in the direction x (=r ), as follows,
(Eq.27)
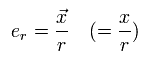
From Eq.22, Eq.25, Eq.26, and Eq.27,
(Eq.28)
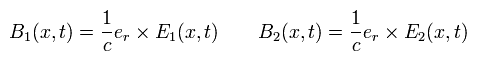
As shown in Eq.25 and Eq.26, even when a charged particle is moving at the constant velocity (= first derivative of dipole p ), the electric and magnetic fields around it are generated and changing (= E1 and B1 ).
But those people who try to deny Bohr orbit ignore this result and pick up only the accelerated dipole part (= E2 and B2 ).
Of course, in the place where r is close to infinity, only E2 and B2 tend to be left as shown in Eq.25 and Eq.26.
But it is impossible that we arrive at the places where r is infinity.
And in the places near the moving charged particle, E1 and B1 are stronger than E2 and B2 (considering c, too).
So according to these explanation, the charged particle moving at the constant velocity also radiates electromagnetic wave energy !
This is strange.
According to Maxwell laws (in the radiating energy), the poynting vector S is thought as representing the directional energy flux density (the rate of energy transfer per unit area) of an electromagnetic field.
Using E2 and B2 of Eq.25 and Eq.26, S is
(Eq.29)
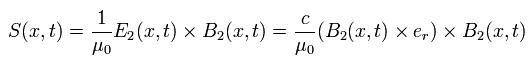
Here we use the next formula of
(Eq.30)
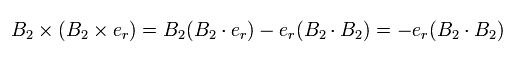
As a result,
(Eq.31)
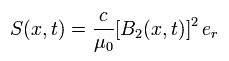
From Eq.26 and Eq.31, the poynting vector S by the "accelerated" dopole is
(Eq.32)
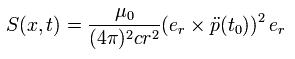
When we integrate Eq.32 on an entire spherical surface area, we get "Larmor's formula".
And the poynting vector S1 by the "constant velocity" dopole is
(Eq.33)
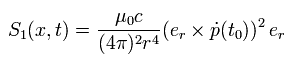
In Bohr's orbit, an electron is moving around the proton.
When we pay attention to each short segment of the orbit, an electron is moving like an free electron.
And of course, in the places where r is infinity, the hydrogen atom is neutral, and the electric dipole itself is zero and can be neglected.
In case of radiating electromagnetic energy wave by the accelerated charge, many charged particles need to be oscillating (or interacting with each other) at the same place.
So it is unnatural that we think Bohr's orbit radiates energy wave only due to the above explanation.
(Of course, "stable" de Broglie's waves need to be considered, too. )
The pointing vector of Eq.32 and Eq.33 is based on the next electric energy (= ue ) of the vacuum,
(Eq.34)
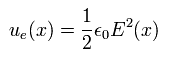
By the way, the very classical notion of Eq.34 is really correct ?
( In fact, the energy of the emitted electromagnetic wave is known to be related to its frequency rather than its amplitude. )
When we try to get the relation of Eq.34, we need to think about a spherical conductor with a radius of a.
And the total charge Q is distributed equally over the surface of the sphere.
(In fact, this notion is very "classical", because the charge of electron (-e) or proton (+e) can NOT be divided !)
(Fig.3) Spherical conductor ( radius = a , and total charge = Q )
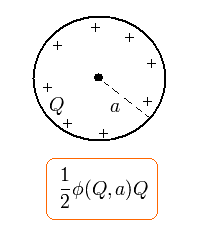
When the total charge of the spherical conductor is q, the potential energy (= φ ) on the surface area is
(Eq.35)
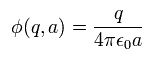
So the energy needed for giving the charge Q to the surface of the sperical conductor is
(Eq.36)
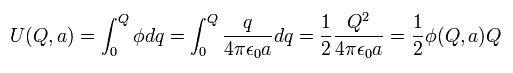
Eq.36 is indispensable to get the relation of Eq.34.
But if the spherical conductor is a single electron, the energy needed for giving an electron the charge -e becomes infinite !
(Eq.37)
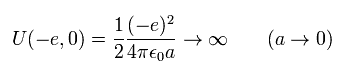
Because an electron is a point particle, and the radius a is zero.
(Of course, as you know, the charge -e of an electron can NOT be divided !)
(Fig.4) Single electron = spherical conductor ??
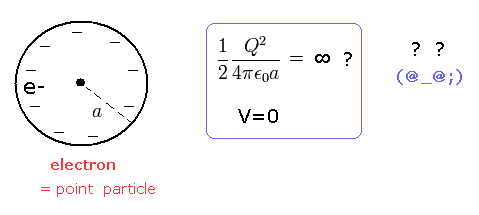
When there is only one electron in some area, its energy (= V ) is zero, because no repulsive (or attractive) Coulomb interaction is generated in one-particle area.
So the idea of Eq.36 can NOT be used in a single electron (or a proton ) !
(Fig.5) Surface of charged spherical conductor
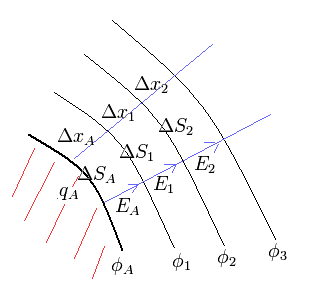
First we consider a infinitesimal area (= ΔSA ) on the surface of the spherical conductor.
The surface density of the charge is supposed to be qA.
And the potential energy of the surface of the sphere is φA.
Using Eq.36, the electrostatic field energy is the sum of all infinitesimal areas, as follows,
(Eq.38)
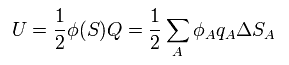
Using Gauss law,
(Eq.39)
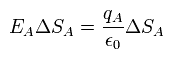
where EA means the electric field on the surface.
As shown in Fig.5,
(Eq.40)
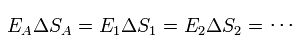
And
(Eq.41)
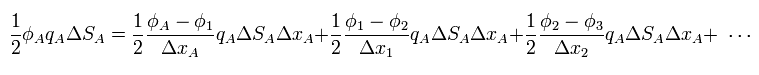
where we suppose ΔxA = Δx1 = Δx2 ... and the potential φ at infinity is zero.
The electric field E is a gradient of the potential φ, as follows,
(Eq.42)
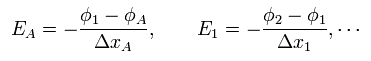
From Eq.39, Eq.40, Eq.41, and Eq.42, we have
(Eq.43)
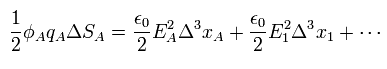
As a result. summing all areas,
(Eq.44)
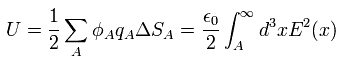
So they insist that the electric vacuum energy at the point x is
(Eq.45)
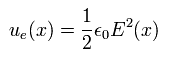
From Maxwell's equations, we can get the next relation,
(Eq.46)
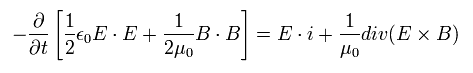
If we consider the left hand side of Eq.46 is the differentiation of the total electromagnetic vacuum energy U, and the current is zero (i=0) in the vacuum, we have
(Eq.47)
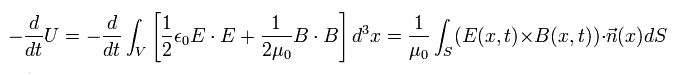
where the right side of Eq.47 means the poynting vector S of Eq.29.
So does this result mean a single electron of Bohr's hydrogen orbit is radiating electromagnetic energy and falling into the nucleus ?
The answer is NO.
As shown in Eq.36, the electric static energy U is caused by the Coulomb interactive energy between infinite very tiny charges (= dq ) included in a spherical conductor with a radius of a.
But as you know, a single electron ( charge -e ) can NOT be divided, so this static energy U is meaningless from the beginning in a single electron (or a proton ).
( Calculation methods of Eq.36 can NOT be used in a single electron ! )
A single electron is NOT made from infinite tiny charges, which is much smaller than -e.
(Fig.6) Single electron's (or proton's ) charge -e = q1 + q2 + q3 ??
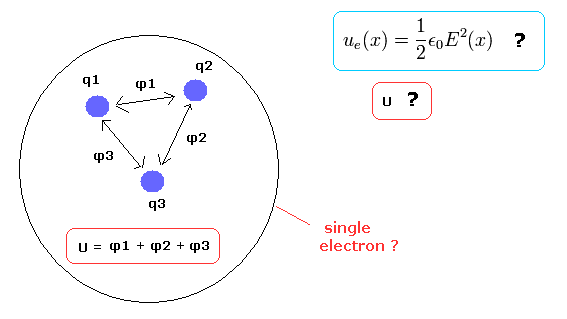
This means when we use the vacuum energy U of Eq.45 (and Eq.36), each charge dq must be infinitesimal (of course, much smaller than the charge e ).
If we use single electron or single proton as dq, the total charge Q must be much greater than the charge e, instead.
In this case, we can treat the charge e as infinitesimal one ( e → 0 ).
This is a origin of the misunderstanding about Bohr's orbit.
Classical Maxwell's laws did NOT think about the quantization of the charge (= e ).
We get the poynting vector from the accelerated electric dipole in Eq.32.
In Eq.32, we suppose the angle between the acceleration of the dipole p and er is θ
So the magnitude of S in the r direction of Eq.32 becomes
(Eq.48)

The total energy flux through the spherical surface with a radius of r is
(Eq.49)
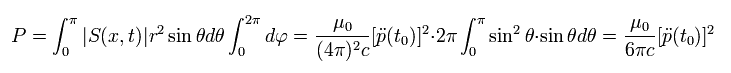
where we use
(Eq.50)
When the point particle's (= charge e ) position's function is z(t), the electric dipole moment p(t) is
(Eq.51)
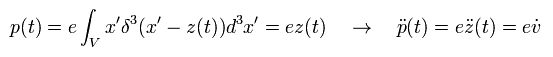
Substituting Eq.51 into Eq.49, we obtain
(Eq.52)
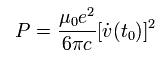
Eq.52 means the energy emitted by the "accelerating" point particle (charge e) per unit time.
This is called "Larmor's formula".
Here we use the usual SI unit. Next we change this into cgs units.
In cgs units, the electricmegnetic fields ( E', H') and the poynting vector (S') is
(Eq.53)
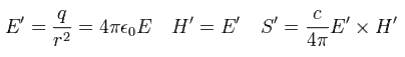
Form Eq.53
(Eq.54)
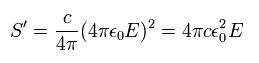
From Eq.22, Eq.28, and Eq.29, the poynting vector in SI units is
(Eq.55)
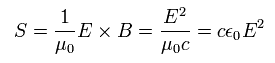
From Eq.52, Eq.54 and Eq.55, Larmor's formula in cgs units is
(Eq.56)
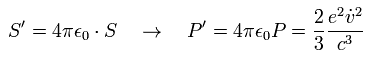
Based on the results of Eq.52 (or Eq.56), they insist that the Bohr's hydrogen electron radiates energy and spirals into the nucleus.
But in these cases, they use the sum of the usual potential energy and the kinetic energy in the Bohr's hydrogen.
(This contradicts the first assumptions ! )
But as I said above in Eq.44, the electric energy in the vacuum originates in the potential energy stored in the spherical conductor !
( Of course, these potential energies between infinitesimal charges must be based on genuine Maxwell's equations.)
But in the point particle electron, this electric energy becomes infinite, as shown in Eq.37 !
This means the electron has "infinite" stocks of energies in it and can radiate its energies "forever", NOT falling into the nucleus.
So as a result, the point-lile electron with infinite energy doesn't spiral into the nucleus losing energy.
(Of course, it is impossible that we make the point-like electron from infinitesimal charges or break the electron into smaller pieces !)
Even the classical electron radius, which energy (= Coulomb potential energy ) is equal to mc2 is as large as the proton.
Next we derive the poynting vector S in Eq.46 using the usual Maxwell's equations.
Maxwell's equations are
(Eq.57)
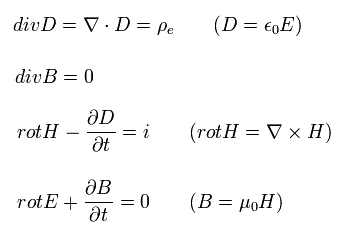
where E and B mean the electric field and magnetic flux density, respectively.
The inner product of E and the third equation of Eq.57 and the inner product of H and the fourth equation of Eq.57 are
(Eq.58)
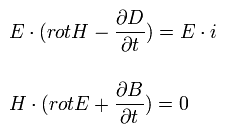
The upper equation minus the lower equation of Eq.58 is
(Eq.59)
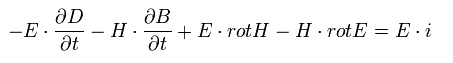
Using the formula of
(Eq.60)
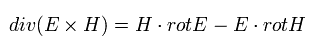
and the relation of
(Eq.61)
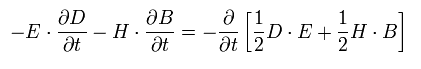
we obtain Eq.46.
As I said, the point-like electron electric energy is infinite, so it never loses the energy.
According to Maxwell's law, the electric and magnetic energies included in Eq.61 are equal to each other. (Use also Eq.28)
Here we try to visualize this relation using the next system.
(Fig.7) One capacitor (condenser) + one solenoid
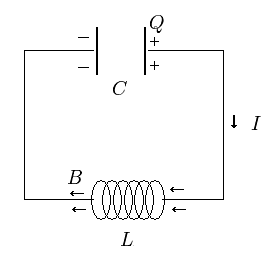
The magnetic flux (Φ), the magnetic flux density (B) of the solenoid, and the potential energy differernce (φ) between the two conductor plates of the capacitor are
(Eq.62)
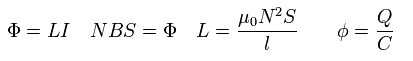
where C means a constant value capacitance, which is the ratio of the electric charge (Q) on each conductor to the potenrial differernce (φ) between them.
And L means "inductance" of the solenoid. "I" is the electric current.
N is the number of turns in solenoid, l and S mean the length and the area of the solenoid.
(Caution: magnetic flux (Φ) is usually equal to BS. But in this case we want to know the induced voltage. The induced voltage (V) is in proportion to the turn number (N).)
So the induced voltage (V) known as Faraday's (- Lentz) law is
(Eq.63)
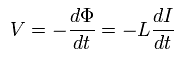
As shown in Fig.7 the sum of the voltages of the capacitor and solenoid is zero, as follows,
(Eq.64)
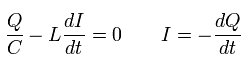
From Eq.64, we find how the charge (Q) stored in the capacitor and the current (I) are changing with time.
(Eq.65)
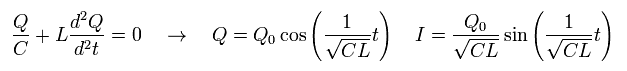
According to Eq.65, the charge Q at the capacitor and the current I at the time of t = 0,
(Eq.66)
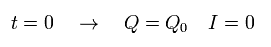
And at the time of
(Eq.67)
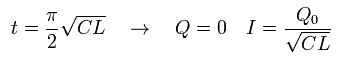
And at the time of
(Eq.68)
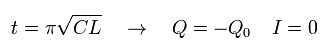
At the time of Eq.66 and Eq.68, the charge stored in the capacitor becomes maximum (= ± Q0 ).
To store the charge Q in the capacitor, we need the energy of
(Eq.69)
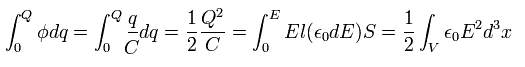
where
(Eq.70)
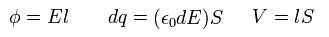
Caution: here l and S mean the length and the area of the capacitor.
This result is the same as the electric energy density in the vacuum (= Eq.45).
The important point is that if we want to use this electric energy of Eq.45 or Eq.69, the charges need to be stored based on Maxwell's laws.
But as I said above, the charge of the electron is NOT stored obeyng Maxwell's laws.
It exists from the beginning, and can NOT be divided.
So the electric energy around a single electron can not be used as an energy of the poynting vector.
And we have
(Eq.71)
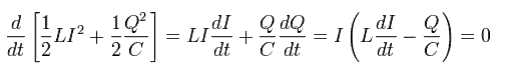
where we use Eq.64.
Eq.71 means the conservation of the total energy (of the charged classical conductor).
Using Eq.62 and Maxwell equation of Eq.57, we obtain
(Eq.72)
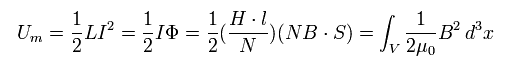
where we use the relations of
(Eq.73)
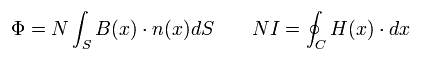
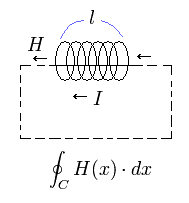
Outside of the long solenoid, the magnetic field H is approximately zero. So NI = Hl. (See Fig.8.)
(Fig.8)
At the time of t=0 (= Eq.66), the current (I) is zero, and the charge Q stored in the capacitor is maximum.
(Eq.74)
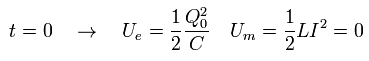
In this case, the energy is stored only in the capacitor. (The solenoid energy is zero.)
On the other hand, at the time of Eq.67, the capacitor charge is zero, and the current is maximum.
(Eq.75)
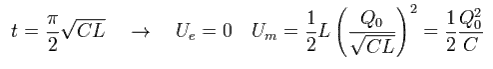
The energy of Eq.74 is just equal to Eq.75.
As a result, the magnetic energy of Eq.72 is equal to the electric energy of Eq.69.
(Of course, choosing the system of Fig.7 leads to this result. )
As shown in this page, when we want to define the electric (Eq.69) and magnetic energy (Eq.72) as "energies", they need more than one charges.
In the electric energy, between at least two charged particles, the electric potential energy is generated.
Because the potential energy = electric field (E) × charge.
(So in case of a single electron, the electric field can not be defined as "energy". )
In the magnetic energy, suppose one charged particle ( which can not be divided ) is rotating and its speed is changing, which means the magnetic field in it is changing and causes the induced voltage along its orbit.
In this induced voltage, another charged particle needs to go along the first one's orbit to store the magnetic energy.
So also in case of the magnetic energy, the energy is charge × voltage, as the electric potential.
When there is only one electron, only the induced voltage exists. We need another charge to store energy.
So a single electron doesn't radiate energy, even if it is accelerating.
Only when the potential energy (+ kinetic energy) between the electron and proton changes, they emit (or absorb) energy.
Of course this result is consistent with the experimental results.
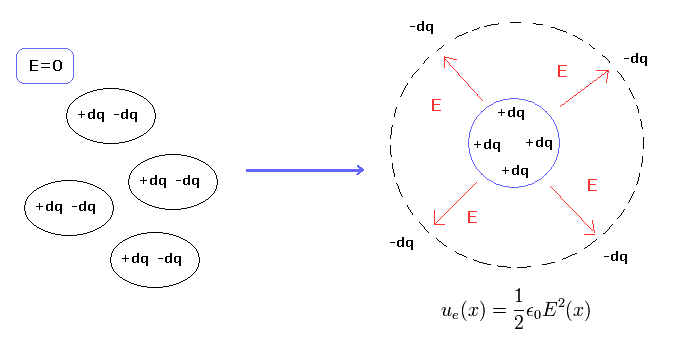
(Fig.9) Electric field (E) in Maxwell's world.
In Maxwell's world, only Maxwell's equations of Eq.57 is valid.
( This means we have to express all phenomena using only Maxwell's equations. )
And Maxwell's world uses "infinitesimal" charges (= dq ) or charge density (= ρ ), NOT quantized charge (e).
So the generation of the electric field (E) means the unbalanced distiribution of plus and minus infinitesimal charges (Fig.9 right).
As a result, the geneation of the electric field itself requires the energy of Eq.36 naturally, (which means electric energy. See also Eq.44 ).
(Fig.10) Single electron's world.
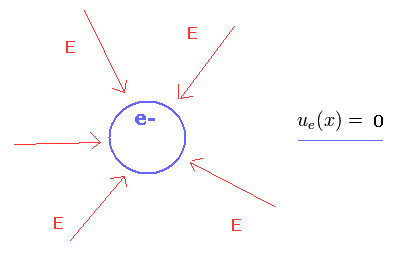
On the other hand, in a single electron's world, the charge (e) is "quantized".
So from the beginning, the charge e exists. It means the electric field (E) exists from the beginning, too.
As a result, in a single electron's world, the existence of the electric field is NOT equal to the existence of the vacuum energy. ( ue = 0. )
(And of course, we can not break a single electron into pieces, so we can not release the infinite energy in it.)
(Fig.11) Magnetic field (B) in Maxwell's world.
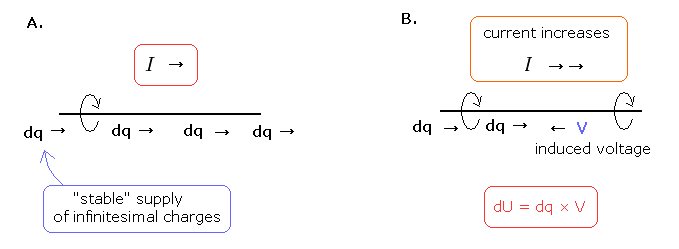
In the magnetic field of Maxwell world, we use the current (density) i as a origin. (Eq.57)
The electric current (= I ) is what we call "one-dimensional line", not a point-like particle.
So in Maxwell's world, infinitesimal charges (= dq ) are supplied "stably" and "automatically" from one side to another, as shown in Fig.11.
When the current is increased, the magnetic field around it increases and it causes the induced voltage (V), which tries to weaken the increased magnetic field (= tries to weaken the current ).
So we "naturally" need the energy to increase the current. ( energy = induced voltage × charge dq. )
This is what we call "magnetic energy" of Eq.72.
(Fig.12) Magnetic field (B) in a single electron's world
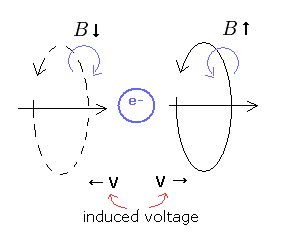
On the other hand, in a single electron's world, there is only one electron.
So when we generate the electric current, " one-dimensional current I " is NOT generated.
In the front of the electron, the magnetic field (= B ) increases, because the electron approaches toward it.
As a result, the induced voltage V occurs, which tries to weaken the magnetic field ( and current ).
But behind the electron, the magnetic field decreases, because the electron moves away from it.
So it causes the induced voltage V, which tries to strengthen the magnetic field (and current ).
These induced voltages are opposite, and cancel each other.
As a result, in a signle electron's world, the magnetic energy is not needed to generate the magnetic field.
Of course, the magnetic field is generated by the electric field. So if the electric field itself has no energy as shown Fig.10, the magnetic field has no energy, too.
As a result, the electric and magnetic energies themselves of Eq.61 don't exist in a single electron's world, and the poynting vector of Eq.46 itself is meaningless.
The idea like "Bohr's hydrogen electron radiates energy and falls into the nucleus" was probably made by people, who try to let students give up easy-to-understand Bohr model later than Maxwell's time.
Maxwell's theory itself is valid even now, if we consider the quatization of the electric charge (= e ).
The magnetic energy of Eq.72 is a little difficult to imagine.
Here we suppose a single rigid sphere which is accelerating.
And the infinitesimal charges (= dq ) are distributed in it, like Fig.13.
(Fig.13) Single electron = rigid sphere ?
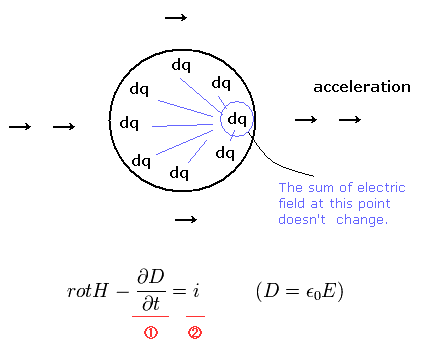
Of course, a single electron is not a rigid sphere, so the electric energy of Eq.61 is not true in a single electron's world.
So the poynting vector does NOT mean the energy flux in a single electron's world.
The induced magnetic field (= H ) satisfies the third equation of Eq.57 and Fig.13 (= Ampere's law).
The number 1 and 2 terms of Ampere's law (in Fig.13) are independent from each other.
The number 2 term uses very long one-dimensional electric current i.
In this case, even if the sum of the electric field (E) is zero, the current (= i ) exists and it induces the magnetic field around it.
(Also in the long solenoid, even when the total charge ( summing all plus and minus charges ) is neutral, the current i exists.)
The single charged particle case corresponds to the number 1 term of Fig.13.
So the changing electric field (= E ) around the moving charged particle causes the magnetic field.
We must not count the same magnetic field twice. The number 2 term of Fig.13 needs to be limited to the current i which causes "constant" electric field.
But if the rigid sphere of Fig.13 is a spherical conductor, the electric field (E) in it is always zero.
As a result, the magnetic field (= H) is not induced by the electric field, which means there are no induced voltages V.
And if the infinitesimal charges (= dq) are fixed inside the rigid sphere, and they are always moving together with the rigid sphere, the electric field (= E ) inside the rigid sphere is always constant, as shown in Fig.13.
(Because the positional relationship of the infinitesimal charges inside the sphere doesn't change.)
So it does not cause the induced magnetic field and induced voltage inside the rigid sphere, even when it is accelerating.
As I said above, the magnetic energy is induced voltage V × electric charge (= dq ) or current.
So the accelerating single charged patricle doesn't have the magnetic energy, too.
(We need more than one separated charged particles to have the magnetic energy.)
In conclution, "accelerating Bohr's electron radiates energy and falls into nucleus" is completely wrong idea, even if we don't consider de Broglie wavelength.
As I said above, the electric energy of Eq.61 is meaningless in a single electron's world, because a single electron can NOT be broken and can NOT release the infinite energy in it.
( So accelerating Bohr's "unbroken" electron does not radiate energy. )
And the megnetic field is generated by the electric field, so the magnetic field has no energy, either.
( Magnetic charge does not exist. Only electric charge exists in this world. )
(Fig.14) Magnetic field = electric field.
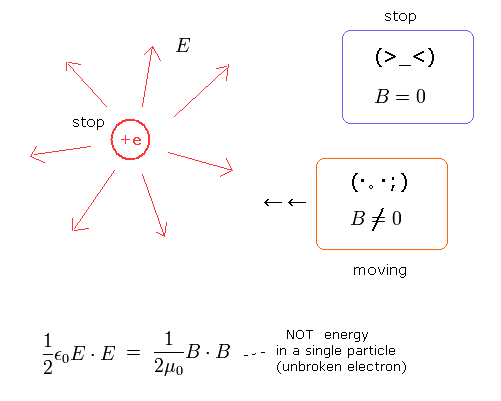
According to the relativity (= principle of equivalence ), the magnetic and electric fields are the same things and appear and disappear depending on the observer's viewpoints.
In Fig.14, the electric charge (+e) is at rest. So from the viewpoint of the observer at rest, the magnetic field (B) is not visible. ( Of course, the electric field (E) exists. )
But from the moving observer, the magnetic field is generated.
This means the electric field and magnetic field depend on the observer's viewpoint.
So if the electric field does not have energy, the magnetic field does not have energy, either.
(Fig.15) Magnetic field = electric field.
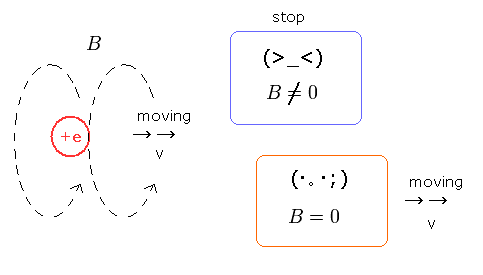
In Fig.15, the electric charge is moving at the velocity v .
In this case, from the stopping observer's viewpoint, the magnetic field is visible.
But the observer who is moving at the same velocity v can not feel the magnetic field (= he can feel only the electric field).
This is due to the fact that the magnetic charge does not exist.
The magnetic field is caused by the relative velocity between the two electric fields.
( This is similar to a kind of "friction". )
Special relativity was made based on these facts of the electromagnetism at first.
But it denies "ether", so it can NOT explain Coulomb force without "mathematical" virtual photons.
And it uses strange concepts such as "time" delay.
So we need to correct these points, I think.
If we deny "ether", we have to define the electric and magnetic field using other things such as "virtual" photons.
So even if a single electron can not be broken, and can not release infinite energy in it, we have to give energies to the electric field around a single electron.
Because all electric fields are expressed as the sum of a single electron's (or proton's ) electric fields.
As shown in Eq.64 in this page, the QED Hamiltonian (= energy ) of the electromagnetic field can be expressed as
(Eq.64')
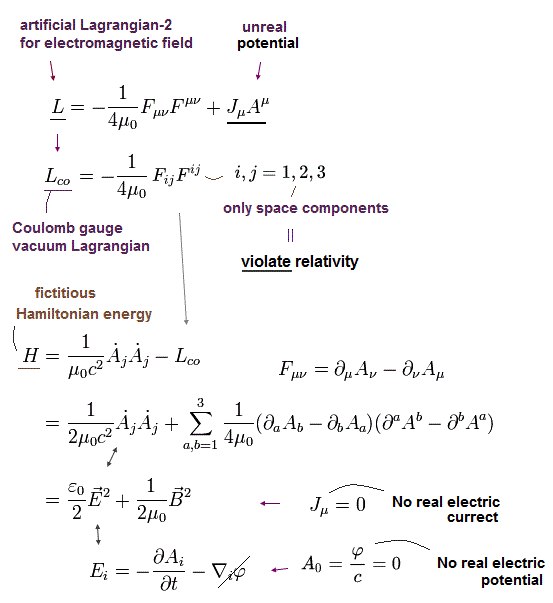
Of course in the Coulomb gauge, Lorentz invariance is violated, which causes "mathematical" virtual photons in Coulomb forces.
To stop these contradictions ( and strange electric energy mentioned above ), we have to give up "photon particle" to express electromagnetic fields. ( This means we have to give up "QED". )
As shown in this page, Maxwell's equations, electric (= E ) and magnetic fields (= B ) are essential to the quantum field theory.
So, the result of Eq.64' is natural in QED. The important point is that we have to judge whether Eq.64' means the (electromagnetic) energy even in a single electron's world.
In QED, we separate the electromagnetic fields as (virtual) photons from the single electron which is a origin of the fields.
So we can not judge correctly in QED.
All vacuums are filled with "virtual" photons ?
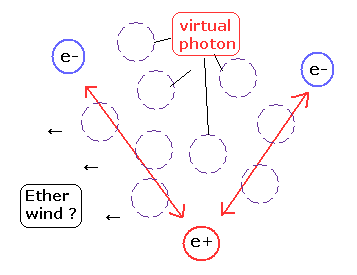
And as shown in this page, if the vacuum is filled with (virtual) photons, it causes what we call "ether wind", which contradicts special relativity.
( If you say "virtual" photons don't actually exist, what on earth causes the "real" Coulomb force ? This is inconsistent. )
In Fig.13, each infinitesimal charge doesn't feel the change of electric field (and current), so the induced voltage doesn't occur at each charge.
In the case of electric current (= i ), there are some points we have to pay attention to.
(Fig.16) Electric current = relative motions of plus and minus charges.
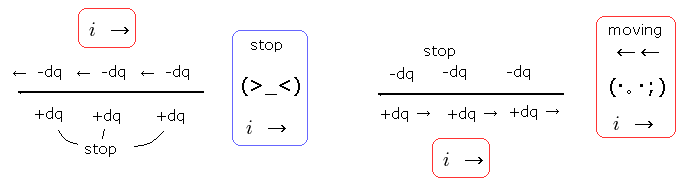
Even if the total electric field is zero, the magnetic field can be generated by the electric current (= i ).
The electric current contains a lot of plus and minus charges, and they are moving in the opposite directions.
So as the current increases, collisions between plus and minus charges increase, too.
It leads to the increased magnetic field around them.
As a result, we need energy to increase the magnetic fields around the current i.
As shown in Fig.16, the electric current i is independent from the observer's viewpoint, which is different from the above electric field.
Because the relative motions between plus and minus charges do not change depending on the observer's viewpoint.
If we want to use the number 2 term of Fig.13 as a generator of the magnetic field in the point-like charge, it needs to be limited to the infinitesimal area around the point-like charge.
(In this infinitesimal area, the point-like charge looks like a "very long" current.)
In almost all area which includes only one point charge, the magnetic field is generated by the number 1 term of Fig.13.
To put it accurately, we must not count the same magnetic field twice in Maxwell's equations.
The number 2 term of Fig.13 needs to be limited to the current i which causes "constant" electric field.
So the moving single point-like electron can not be used as the electric current i of Maxwell's equation.
(Fig.17) Electric current = stable supplies of charges.
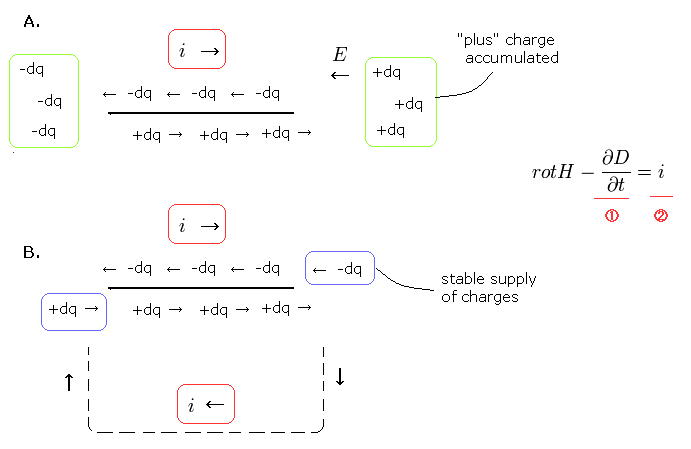
In fact, the electric current i changes the electric fields (= E), which causes the induced magnetic field (= H) around them.
When the plus charges flow into the right side, the plus charges are accumulated at the right end ( Fig.17A ).
As a result, the electric field E changes.
But the electric current i of Maxwell equation is stably supplied with plus and minus charges from both ends ( Fig.17B ).
So the total elecgtric field doesn't change. The time difference of them causes the magnetic field.
Of course, in the circular electric circuit, two currents in the opposite directions from each other exist at the same time.
As a result, the center of the total charges doesn't move in the current i.
In a single electron's world, it can not generate two opposite currents at the same time.
So the changing electric fields is the only way which generates the magnetic field for a single electron.
(Fig.18) Poynting vector is obtained from the electric field (= D ) changes in a single electron's current.
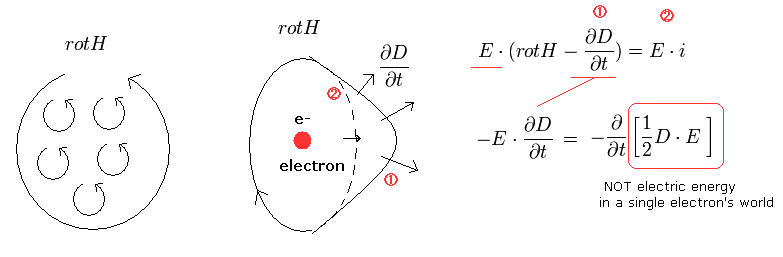
As shown in Fig.18, rot H (= curl H ) is the sum of small magnetic circles included in the curved surface surrounded by the closed curve H.
We can choose any curved surface surrounded by the H.
In a single electron's world, the current i is discontinuous, so curl H (= rot H ) can always be expressed as the change of the electric field (= the time derivative of D ), which corresponds to the number 1 term of Fig.18.
( We need not use the current i in a single electron's world. )
As I said above, a single electron is NOT made from infinitesimal charges and can not be broken into pieces.
So the electric energy of Eq.45 is meaningless.
As shown in Eq.58, Eq.59 and Eq.60, Poynting vector needs this electric energy.
This means the Poynting vector is meaningless in a single electron's world.
(Fig.19) Rot H in a "continuous" electric current i.
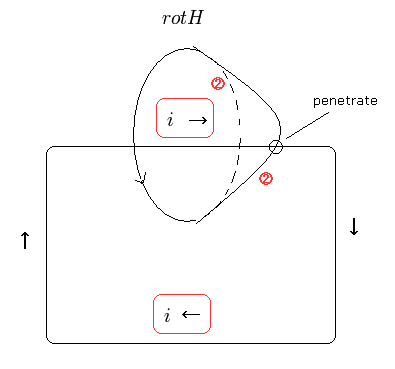
On the other hand, in the continuous electric current i, the curved surface surrounded by rot H always includes the electric current i.
So the number 2 term of Fig.18 is valid in this case.
As I explained above, the magnetic energy ( such as Eq.72 ) which we need to increase the magnetic field is given by charge (q) × induced voltage V.
In a single electron's case (Fig.18), each increased magnetic field ( H ) is expressed as the sum of the small rot H circles on an arbitrary curved surface surrounded by the H.
And this curved surface does NOT need to include the electric current (= e- ), as shown in Fig.18.
On this curved surface, induced voltage V occurs by the changing magnetic fields.
But this curved surface does not include the electric charge, so the magnetic energy is not needed.
( Magnetic energy = charged current × induced voltage V. )
On the other hand, in Fig.19, any curved surface surrounded by rot H (= not zero ) always includes the electric current i.
And at each point where the current i is increased, the induced voltage V occurs.
As a result, to increase the magnetic field in Fig.19, the magnetic energy is needed.
(Fig.20) Electric energy is valid in a "continuous" electric current i.
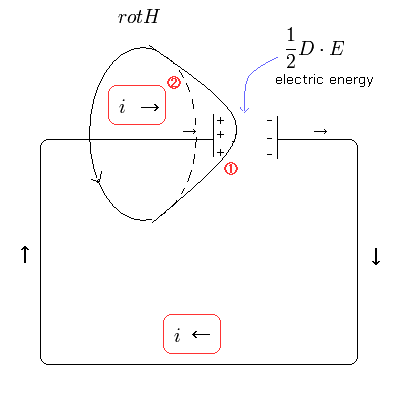
If there is a capacitor in this circuit, we can choose the curved surface (= number 1 ) which includes the capacitor, as shown in Fig.20.
In this case, rot H is expressed as the change of the electric field D.
But this electric field in the capacitor means the electric energy, as shown in Eq.69.
Because the electric circuit of Fig.20 consists of many infinitesimal plus and minus charges.
In Fig,7, the decrease in the electric energy of the capacitor is equal to the increase in the magnetic energy of the solenoid.
So also in Fig.7, the energy loss by the Poynting vector is zero.
Anyway, to describe the magnetic and electric fields correctly, we need to use the Coulomb field around a single electron (or proton), because all electromagnetic fields are the sum of them.
We have to reconsider relativity to explain " inverse-square laws " such as Coulomb force and gravitation.
And we need to go back to Newtonian mechanics and Maxwell's laws (+ de Broglie theory ) again, I think.
Some people say that relativity is inconsisntent with quantum mechanics.
But in fact, they have an extremely close relationship.
"Loss of reality" in wavefunction means special relativity !
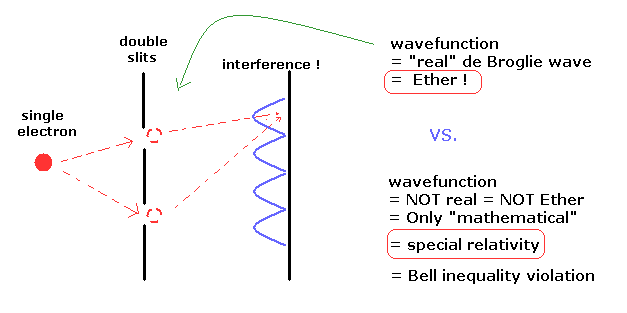
Even a single electron can interfere with itself in the double-slit experiment.
According to the quantum mechanical interpretation, this electron's wavefunction means only "mathematical" probability amplitude, which is NOT real.
( If we interpret this wavefunction as a real thing, the electron can move faster than light, when the wavefunction collapses ! )
And as shown in this page, they insist that quantum mechanics is "nonlocal" and "unrealistic" mentioning Bell inequality violation.
If the wavefunction is "real", this real wavefunction can be considered as a "real" de Broglie wave, which goes through the " ether " in the vacuum.
So if we admit the reality of the wavefunction (= "ether" ), we have to deny the special relativity.
As a result, "unrealistic" and "nonlocal" interpretation of wavefunction as shown in Bell inequality violation supports "special relativity".
( Strange to say, nonlocal = special relativity ! )
Very heavy W boson violates energy conservation completely.
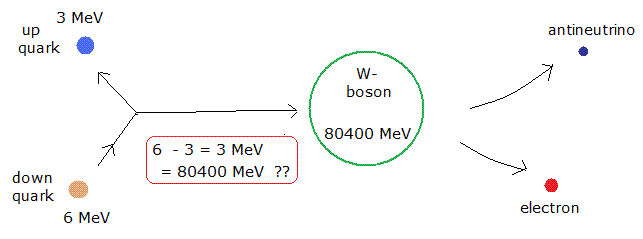
As shown this page, beta decay violates energy conservation, if we use W boson, which is about 80 times a proton.
The energy difference between down and up quark is only 6 - 3 = 3 MeV. But the W boson in the acceleratos is as big as 80400 MeV !
They try to explain this strange phenomenon using uncertainty principle (of time and energy ).
So if Bohr model is correct, and Schrodinger equation is wrong, this means uncertainty principle is wrong.
( See Schrodinger equation is a wrong version of Bohr Sommerfeld model ! )
As a result, the standard model which uses very heavy W boson is wrong, too, if Bohr-Sommerfeld model is correct.
As I said above, special relativity denies ether, so it uses " virtual photon " to express Coulomb force.
This virtual photon violates relativistic causality and energy conservation.
Because this virtual photons with some energy can emerge from the vacuum, even if we don't give any energy to them.
( And when they disappear at the target charged particle, this energy disappear, too.)
Of cource, this strange process in virtual photons needs "uncertainty principle".
As a result, special relativity = virtual photons = uncertanty principle !
So if the uncertainty principle is wrong, the special relativity is wrong, too.
Coulomb relation (and gravity ) changes under Lorentz transformation.
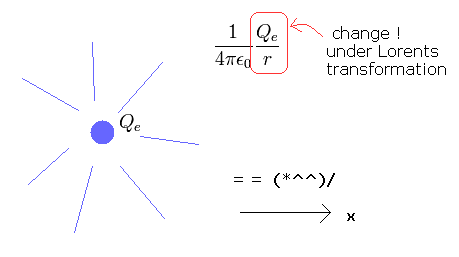
In the special relativity, the important equations need to be invariant under Lorentz transformation.
But the Coulomb and gravitational relations change under Lorentz transformation, because we consider the central charged particle ( or star ), the origin of the force, as special.
So in Coulomb gauge, which express Coulomb relation, Lorentz invariance is violated.
( Strange to say, zero component of photon (= scalar photon ) is "unreal" thing. )
We treat the Coulomb relation as a " approximate " thing using virtual particle. It is a kind of "deception", I think.
But in gravity, we can NOT use this deception.
Because the gravity is a basic thing governing time and space according to the general relativity.
So we have to depend on what we call " extra dimensions " to explain gravity, as long as the general relativity is correct.
If we admit the ether which is moving with and attracted to the earth, we can explain the light or GPS influenced by the earth.
( In fact, GPS time correction is very complicated. We have to consider many things such as air condition. )
GPS time uses the light frequency emitted by some atoms, which may be influenced by the moving ether.
------------------------------------------------------------------------
As I said above, if we deny "ether", we have to express the electromagnetic field around a single electron by (virtual) photons.
Of course, Maxwell's equations are indispensable in the quantum electrodynamics (QED).
If we calculate the energy based on Maxwell's equations, we would naturally get the energy of Eq.64'.
As a result, the QED photons can not explain a single electron's world correctly as shown in Poynting vector.
( And they cause the "ether wind", which constradicts the special relativity. )
(Fig.21) Electric field is "distortion" of the ether ?
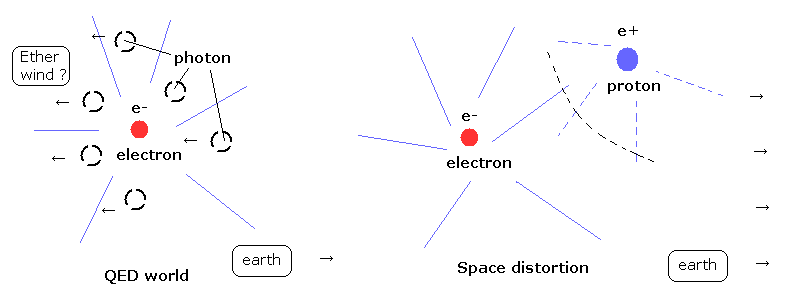
By the way, what on earth are the "ether" and "Coulomb force" ?
( Here we forget "mathematical" (= not real ) models such as different-dimension worlds, because "mathematical" models make sense ONLY in "mathematical" worlds. )
Mediums such as air and water consist of separate particles.
( Of course, each water and air molecule consists of "plus" protons and "minus" electrons.)
But the particles of the solid medium bind to each other.
So we don't know the component of the ether is separated or bind to each other loosely for now.
(Fig.22) Generation of a pair of an electron and a proton ( not positron ) is natural.
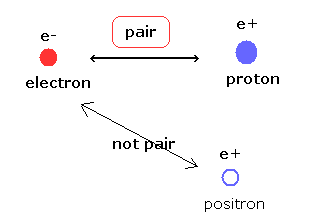
As you know, the magnitudes of the minus (-e) and plus (+e) charges are the same.
So it is quite natural that we think a minus electron and a plus proton are generated at the same time.
As shown in this page, the existence of the positron includes the self-contradiction in the places where the energy is emitted.
And we can NOT explain why all antiparticles disappear and why each antiparticle is fewer than its particle.
In this "real" world, there are a lot of "stable" minus electrons and plus protons (not positron), which attract each other.
So we should think that a "real" partner of an electron corresponds to a proton.
It is no wonder that the masses of an "minus" electron and "plus" proton are different.
( If they are the same like an electron and positron, it is unnatural. ).
To explain the stability of a electron and a proton, we need to think about some energy threshold to form a pair of them.
For example, very stable helium atom is generated from two hydrogen atoms by a nuclear fusion.
When the more stable helium atom is formed, it emits enormous energy.
But the nuclear fusion reaction needs very high temperature, which corresponds to the "thresholds" of the reaction.
Probably like the nuclear fusion, the generation of a pair of an electron and a proton needs a very strict threshold.
Considering the repulsive Coumlomb force between electrons and attractive force between electrons and protons, the minus and plus charges mean some things which cause ether density differernce, I think.
Mass difference between an electron and a proton may be related to this thing.
Probably, heavy protons tend to condense the ether around it, and a "light" electron is a "remaining" thing.
( Of course, "imbalance" of the ether causes "attractive" (or repulsive ) force between them like a spring. )
Under some condition ( in which there is enough ether and each ether's direction is the same ), they can condense, I think.
And in the nuclear fusion, condensed proton becomes more condensed with other protons (+ a few electrons ) above some threshold, which can cause the conformation change.
(Fig.23) Electromagnetic wave is the propagation of "imbalance" of the ether.
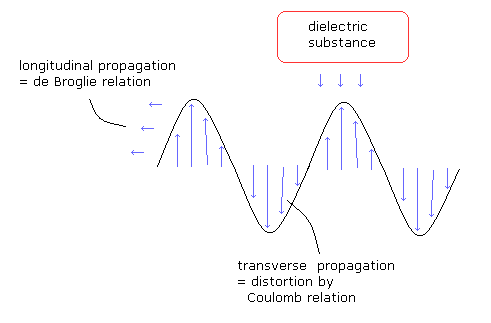
As a result, the electromagnetic wave is thought to be a sort of propagation of the ether density imbalance.
The longitudunal propagation is related to the longitudinal waves such as de Broglie's waves.
The transverse direction means the electric field, which is related to be the ether density imbalance (= gradient ).
(If there are some dielectric substances around them, the ether density imbalance (gradient) is thought to decrease, which influences the propagation speed. )
Of course, these models are only speculations for now.
So I'm very glad if someone could show much better "realistic" Coulomb field models.
And what we call "gravity" is thought to be the drag effect by the aggregate consisting of many plus and minus charges.

2012/2/15 updated. Feel free to link to this site.