Home page
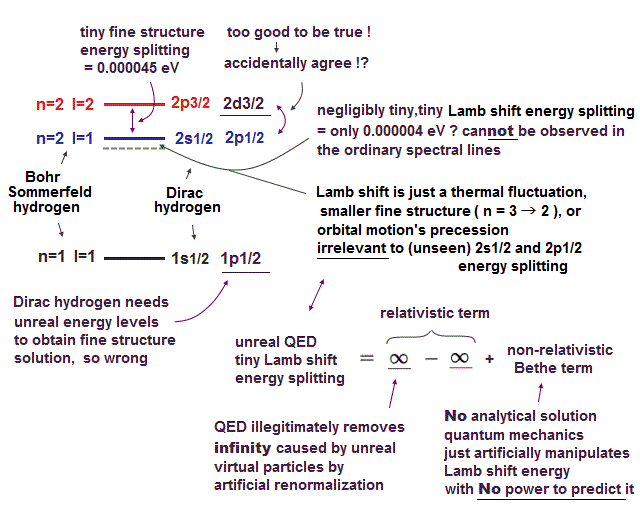
Quantum mechanical fine structure is false.
QED cannot predict Lamb shift
(Fig.1) Quantum mechanical Lamb shift, fine structure are illusion.

Later, they started to say there might be the (negligibly) tiny energy splitting of only 0.000004 eV between (unseen) 2s1/2 and 2p1/2 called Lamb shift allegedly caused by (unreal) virtual particles ( this-middle ).
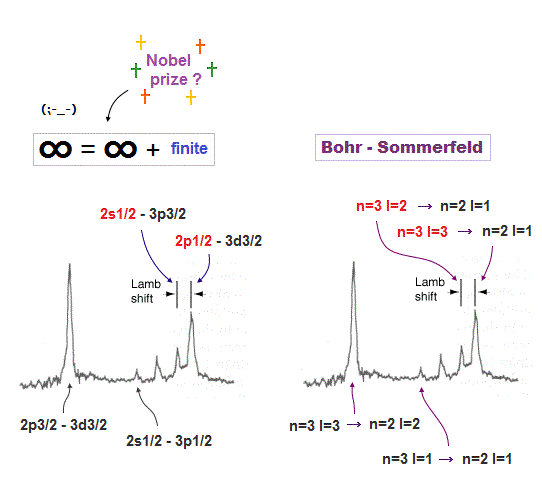
The present mainstream relativistic quantum electrodynamics (= QED ) just giving meaningless infinities are unable to predict Lamb shift.
In fact, this negligibly tiny Lamb shift can be explained by thermal fluctuation, orbital precession, ordinary fine structure irrelevant to quantum mechanical spin, QED virtual particles nor 2s12/-2p1/2 energy levels.
(Fig.2) (unseen) Lamb shift energy splitting between 2s1/2 and 2p1/2 allegedly observed in hydrogen's n = 3 → 2 energy level transition can be explained by ordinary fine structure splitting between 3d5/2 and 3d3/2 (= 3p3/2 ) without electron spin ↓
Today's mainstream quantum mechanical Dirac hydrogen was very unnatural and artificial, because it relied on too many accidental agreements between completely irrelevant orbitals such as 2s1/2 = 2p1/2, 3s1/2 = 3p1/2..
It is said that there is an extremely tiny energy difference called Lamb shift between 2s1/2 and 2p1/2.
But this Lamb shift energy splitting is too small (= only 0.000004 eV ) to measure in ordinary spectral lines.
Doppler free saturation spectroscopy is said to measure this tiny Lamb shift in hydrogen's n = 3 → n = 2 energy level transition.
↑ Because the transition between 2s1/2 and 1s1/2 is said to be forbidden by artificial ad-hoc selection rule (= physicists tried to use two photons or two different lights to investigate the illusory 2s-1s transition, which is difficult, cannot be compared to 2p-1s transition, considering also the irrelevant 1s Lamb shift or thermal fluctuation ).
↑ This tiny Lamb shift energy between fictitious 2s1/2 and 2p1/2 (= 0.035cm-1 = 0.000004 eV, in Nist ) can be naturally explained by the fine structure energy splitting between 3d5/2 and 3d3/2 (= 0.036cm-1 = 0.000004 eV ) in this Balmer n = 3 → n = 2 energy levels' transition.
In this p.9-Fig.4, the Lamb shift transition between 2p1/2-3d3/2 can be replaced by the 3d5/2-2s1/2 transition which energy interval (= between 3d5/2-3p3/2 in 3d5/2-2s1/2 dnd 3p3/2-2s1/2 = ) is almost the same as this Lamb shift energy splitting between 2s1/2 and 2p1/2 (= quantum mechanics does not allow this 3d5/2-2s1/2 transition due to unfounded selection rule ), which can be explained by the real Bohr-Sommerfeld fine structure without spin.
Quantum mechanics tries to artificially forbid (= lacking theoretical reason ) transition between 3d5/2 and 2s1/2 by imposing (baseless) selection rule (= only transitions of total angular momentum Δj = 0, ±1 change are allowed, but this ad-hoc artificial selection rules are often violated ), which ad-hoc baseless selection rule causes this illusory 2s1/2-2p1/2 tiny Lamb shift splitting ( this p.8, this-p.3-exercise 2 ).
↑ The fact that Lamb shift can be explained by the ordinary fine structure splitting means Bohr-Sommerfeld model, which perfectly agreed with fine structure without spin, can explain this Lamb shift where 3d5/2 is a circular orbit of n = 3, orbital angular momentum nφ = 3, and 3d3/2 is an elliptical orbit of n = 3, orbital angular momentum nφ = 2.
In the same way, Lamb shift between 2p1/2 and 2s1/2 (- 0.47cm-1 = 0.000058eV ) of the singly-ionized helium (= hydrogen-like He+ ) also can be explained by 3d5/2-3d3/2 (= or 3p3/2 ) ordinary fine structure energy splitting (= 0.58cm-1 = 0.000072eV = almost the same as 0.000058eV between the illusory 2p1/2 and 2s1/2 Lamb shift energy level considering slight energy uncertainty and fluctuation ).
↑ As shown here, there are many energy transitions baselessly forbidden by artificial quantum mechanical selection rule, so Lamb shift can be naturally explained by ordinary tiny fine structure (= Bohr-Sommerfeld model ) without spin, if we forget the ad-hoc quantum mechanical selection rule.
(Fig.3) Electron collision method of estimating tiny Lamb shift.
Willis Lamb conducted very difficult, doubtful experiment of measuring the tiny, tiny Lamb shift in 1950 ( this p.9 ).
Lamb shift energy splitting allegedly between 2s2/1 and 2p1/2 was too small to measure in ordinary spectral lines, so physicists had to find other methods.
They isolated hydrogen (= H ) atoms from hydrogen molecules at extremely-high temperature of 2500K ( this-p.17-right-4th-paragraph ), which high temperature is as large as 0.2 eV, (= this extremely large thermal background, Stark effect were likely to give false results in this doubtful tiny Lamb shift measurement of only 0.0000004 eV ).
↑ In 1950, there were still No lasers ( this-p.2-first ) nor Doppler-free saturation spectroscopy, so this Lamb's experiment could Not distinguish thermal effect (= causing also magnetic field fluctuation ) from the tiny, tiny Lamb shift ( this-p.4-1st-paragraph ).
And then, they bombarded these H atoms with electron beam to excite H atoms ( this p.2-middle ), which electron beam was likely to cause the background noise or fake signal mistaken on the metastable 2s1/2.
↑ This-p.19-right-1st-paragraph says
"A the electron energies used, the background was three or more times as large as the signal"
And of course, this Lamb's experiment was Not Doppler-free (= atomic or electron's thermal motion easily modified the energy levels ), which cannot detect nor distinguish the extremely tiny Lamb shift.
Under very weak magnetic field, the excited H atom was said to split into multiple energy levels due to anomalous Zeeman effect (= whose energy splitting under magnetic field can Not be predicted by quantum mechanical Lande g factor, so Lamb shift is just a freely-adjustable parameter ).
Only when microwave with specific wavelength changed the alleged metastable 2s1/2 into other unstable state, the excited H atoms returned to the lowest ground state that could not excite target atoms nor generate detectable electronic current.
This experimental method generated a lot of background electrons and currents at extremely-high temperature of 2500K (= as large as 0.2 eV ), so distinguishing very tiny Lamb shift energy splitting (= only 0.000004 eV ) by this experiment is very doubtful.
(Fig.4) Selection rule. Photon with spin-1 forbids 2s-1/2 metastable state from decaying into 1s1/2 ?
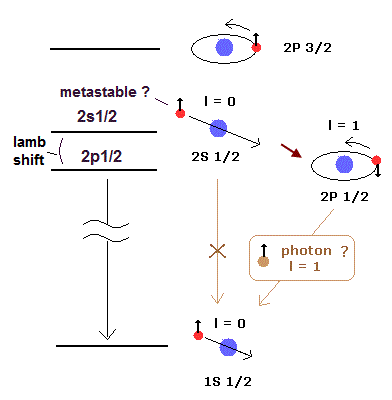
To measure the elusive tiny Lamb shift, they relied on (unfounded) assumption that the unseen 2s1/2 was metastable, far longer-lived than other states such as 2p1/2.
This p.4-right-6. says "Franck and Jordan gave reasons for doubting that 2S1/2 level would be metastable."
This unfounded assumption of the metastable 2s1/2 is based on quantum mechanical artificial selection rule allegedly caused by another unfounded assumption that a photon has spin-1 or 1 angular momentum, which forbids energy transitions of the unchanged orbital angular momentum like 2s1/2 → 1s1/2 ( this p.6-(19),lower ).
↑ But in both transitions of 2s1/2 → 1s1/2 and 2p1/2 → 1s1/2, the total angular momentum j (= orbital L + spin S angular momentums, this p.21 ) is unchanged ( all of 2s1/2, 2p1/2, 1s1/2 have the total angular momentum j = 1/2, so emitted photon should have No angular momentum, but transition between 2p1/2 and 1s1/2 is allowed, which is self-contradiction ), which contradicts the selection rule (ad-hoc) assumption that the emitted photon must have angular momentum 1.
Furthermore, the metastable 2s1/2 energy level is said to be slightly higher than 2p1/2 state ( this p.3 ), which means the 2s1/2 can quickly decay like 2s1/2 → 2p1/2 → 1s1/2 even if the ad-hoc selection rule is true. ← The hypothesis of the metastable 2s1/2 is unreasonable and completely baseless.
This-p.13-right-3rd-paragraph says the contradictory thing
"none of the atoms originally in the lower metastable state β will be excited ← The metastable 2s1/2's β energy level (= p.12-Fig.14 ) under magnetic field is too unstable to detect, only the upper α 2s1/2 was detected as metastable"
↑ This-p.13-right-4th-paragraph says
"transitions βb, βc, βd, βe, βf.. were Not observed" ← This is contradictory. If 2s1/2 was really stable, the lower energy β state of 2s1/2 under magnetic field should have been more stable, long-lived enough to detect.
(Fig.5) Original anomalous Zeeman effect should be symmetric, which contradicted the artificial anomalous Zeeman effect used in Lamb shift experiment.
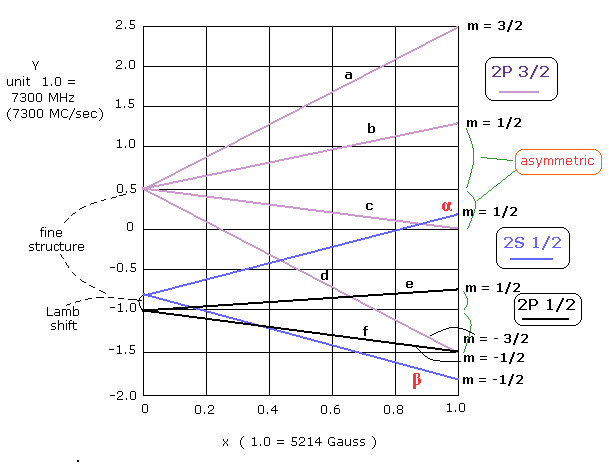
In original anomalous Zeeman effect based on Lande g factor, energy levels must split into symmetrically with respect to applied magnetic field ( this p.2 ). ← Energy intervals between m = 0 and m = +1/2, and m = 0 and m = -1/2 under magnetic field must be equal.
But as shown in the upper figure (= m = 1/2 and m = -1/2 ), Lamb (or unphysical quantum mechanics ) artificially changed this original symmetrical anomalous Zeeman effect into asymmetrical one to fit the desired Lamb shift value ( this p.5, this p.4, this-p.12-Fig.14 ).
According to Lande g factor, 2p3/2 should split into 4 different energy levels under external magnetic field B like ( this p.10 )
a μBB × 4/3 (= Lande-g-factor ) × 3/2 = 2μBB ( m=3/2 )
b μBB × 4/3 × 1/2 = 2/3 μBB ( m=1/2 ) ← symmetric
c μBB × 4/3 × -1/2 = -2/3 μBB ( m= -1/2 ) ← symmetric
d μBB × 4/3 × -3/2 = -2μBB ( m= -3/2 )
↑ When m = ±3/2, the energy change of 2p3/2 under magnetic field B becomes like normal Zeeman effect ±2μBB where μB is Bohr magneton of realistic Bohr-Sommerfeld model without spin.
and 2p1/2 should split into
e μBB × 2/3 (= Lande-g-factor ) × 1/2 = 1/3μBB ( m=1/2 ) ← symmetric
f μBB × 2/3 (= Lande-g-factor ) × -1/2 = -1/3μBB ( m=-1/2 ) ← symmetric
↑ The original Lande g factor must be symmetrical with respect to the magnetic field 0, but anomalous Zeeman effect used by Lamb contradicted this symmetrical Lande g factor (= often disagree with experiments, this p.8-upper ).
And 2s1/2 state is
α μBB × 2 (= Lande-g-factor ) × 1/2 = μBB ( m=1/2 )
β μBB × 2 (= Lande-g-factor ) × -1/2 = -μBB ( m=-1/2 )
So m=±3/2 in 2p3/2 and 2s1/2 become integers × Bohr magneton μB like normal Zeeman effect without spin.
In fact, Lamb shift anomalous Zeeman splitting can be explained only by this normal Zeeman effect without spin (+ thermal fluctuation, the changing fine structure value, and the fake metastable state caused by the external magnetic field )
(Fig.6) ↓ Only a small number of magnetic field points (= circles ) were measured. Other magnetic field points probably disagreed with Lamb shift theory.
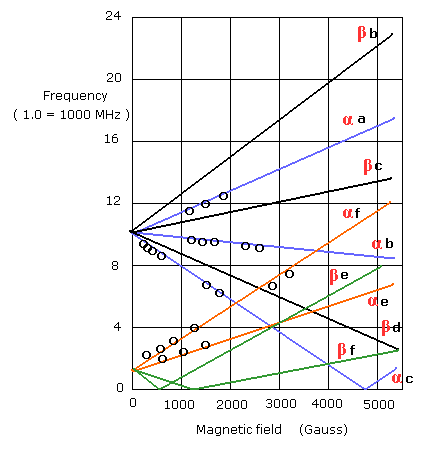
Lamb subjected heated H atoms to magnetic field and microwaves with some specific wavelengths (or frequencies ) to change the ( illusory )metastable 2s1/2 into other unstable states decaying into the lowest ground state (= H atoms decaying into the lowest energy state had no energy left to excite secondary electrons nor generate the detectable electric current, when H atoms hit target atoms, while 2s1/2 metastable states could allegedly excite or generate electric current ) in estimating tiny Lamb shift energy splitting between 2p1/2 and 2s1/2 ( this p.12, p.22 ).
But first of all, this alleged metastable 2s1/2 is slightly higher than the unstable 2p1/2 state, so 2s/1/2, which can decay into 2p1/2 and then 1s1/2, should Not be metastable.
As shown in the upper figure where transitions from 2s1/2 to other states are black circles (= "αf" means transition of 2s1/2-α to 2p1/2-f state ), strangely, they could Not detect any transitions from half of 2s1/2 states (= β or 2s-m = -1/2 ).
This p.13-right-last-paragraph says
"the transitions βb, βc, βd, βe, βf were Not observed" ← The most stable 2s1/2-β states disappeared, which is contradictory.
And they did Not detect even transitions from 2s1/2 α (= m=-1/2 ) under various magnetic fields (= in all magnetic fields without the black circles. the anomalous Zeeman effect based on this doubtful Lamb shift probably disagreed with observation, so they eliminated their contradictory results from the final figure, this p.4 ).
By comparing Fig.6 (= magnetic field B is ① ② ③ ) and Fig.5, you will notice that black circles' anomalous Zeeman effect can be almost explained by transitions between 2p3/2's m = ±:3/2 and 2s1/2 states (= integer × μBB ) which are equal to normal Zeeman effect without spin.
For example, transitions of αc, αb, αa in ② magnetic field = about 1500 Gauss in the upper figure can be explained by normal Zeeman-like transitions of βα, da, αa in ② magnetic field = about 1500 Gauss in Fig.5.
Even by using this microwave, it is impossible to measure the tiny Lamb shift = about 1000 MHz = 0.000004 eV directly with no magnetic field, which means there was always 1000~2000 MHz energy error or uncertainty that could be artificially interpreted to make anomalous Zeeman effect appear to be valid.
Actually, they only measured microwave energy transitions under very weak magnetic field less than 3000 Gauss, and did Not measure under magnetic field stronger than 3000 Gauss (= ③ point ) where their theory of anomalous Zeeman splitting probably disagreed with observation (= so No black circles nor measurements were seen over 3000 Gauss ).
↑ Of course, magnetic field energy used by Lamb was extremely weak (= smaller than tiny fine structure energy splitting ), so electron's orbital motion's precession, slightly-changing electron's mass (= due to Maxwell mc2 ) and thermal fluctuation (= this experiment's temperature was very hot = 2500K with a lot of backgrounds, this p.7-left-1st-paragraph, p.19-right ) might slightly influence and make this normal Zeeman splitting appear to be anomalous.
As a result, this strange (directly-unobservable) anomalous Zeeman effect and metastable 2s1/2 were illusion caused by external magnetic field B which could make electron's excited state stable with lower magnetic energy (= -2μBB, -μBB = negative metastable magnetic energy states, which decayed into the ground state, when they were changed into the less stable +2μBB and +μBB with higher magnetic energy ).
So there is No evidence of tiny Lamb shift between 2s1/2 and 2p1/2.
[1] W.E. Lamb, Jr. and R.C. Rutherford, Phys. Rev., 79 No. 4 549-572 (1950).

Feel free to link to this site.