トップページ (2電子原子も含む正確な新ボーア模型)
標準模型は間違っている。
特殊 ( 一般 ) 相対論は間違い。
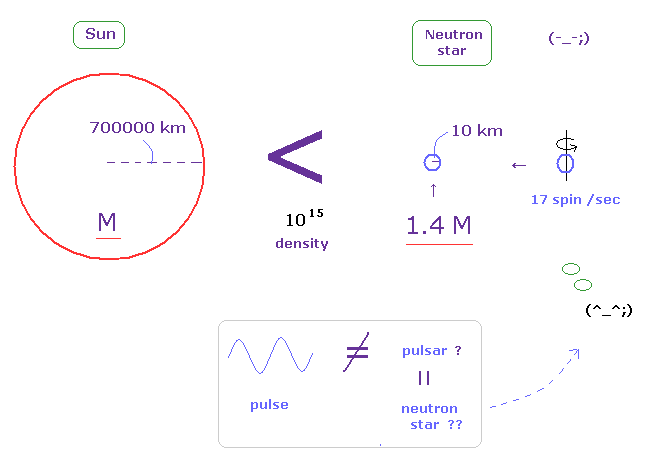
(Fig.1) 中性子星は幻想の産物? ← 一般相対性理論が間違いだと。

中性子星は 質量が大きな星が進化し、重力崩壊によってできた 最晩年の天体の一種である。
中性子星は そのほとんどが 非常に不安定な中性子によってできているとされるが その実態は不明である。
例として 中性子星 PSR 1913+16 は 太陽質量の 1.4 倍 (= 1.4 M ) の重さもあるが、その半径は 非常に小さい (= 10 km )。
つまり この中性子星の 質量密度は なんと 太陽の 1015 倍もあることになる。
中性子星が これほど 非現実的なくらい高密度にも関わらず、なんと 1秒間で 17 回転も自転していると 彼らは主張しているのである。
ご存じのとおり、中性子自体は 非常に不安定な粒子である。彼らは 一般相対論を信じており、その信じられないくらい強力な重力により この不安定な状態を維持できると主張している。
重要な点は この中性子星に関する実験的根拠が 規則正しく振動する 電磁波パルスのみ だという点である。
つまり 致命的なパラドックスによって このパルスの解釈が変われば、当然 中性子星自体の実在性も危うくなる。
普通に考えれば 非現実的な中性子星よりも 宇宙空間中の何らかの物質の規則的な振動が このパルスの源と考えるのが自然である。
実際 この電磁波パルスの具体的な放射機構は 不明なままである。
(Fig.2) "21000" 光年も離れた星 ! → この観測結果は 信頼できるのか?
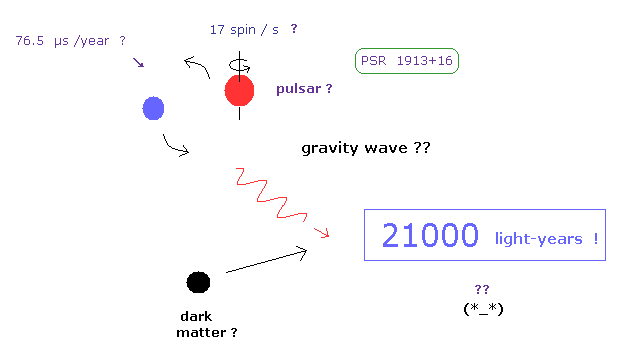
彼らは 重力波は パルサー 1913+16 の軌道周期のわずかな変化の観測によって 間接的に証明できたと主張している。
一般相対論は 軌道周期が 1年で 76.5 マイクロ秒 減少していると予測する ( ← 小さすぎである )。
彼らは 唯一の手がかりである 電磁波パルスのみから 連星系の2つの質量、それらのスピン速度、軌道半径、速度などの すべてのパラメーターを決定しようとしている。 ( ← はっきり言って これは不可能である。 )
問題なのは この中性子星が 地球から 何と 21000 光年も はるかかなたに位置するということである。
例えば、地球上のことでさえ 21000 年 も昔の 歴史上のわずかな変化を知ること自体 不可能である。
ましてや この気の遠くなるような 21000 光年の 長い道のりの途中の よく分かっていない暗黒物質やら 真空の振動などによる様々な影響を 予測することは はっきり言って 不可能である。
つまり この一般相対論のテストというのは 非常に疑わしいと言わざるを得ない。
恐ろしく長い道中の宇宙空間の 何らかの物質の振動が この電磁波パルスを放射、変化させていると考えるのが自然である。
(Fig.3) 一般相対論が正しい → "ファンタジー" を信じるしか道がない。
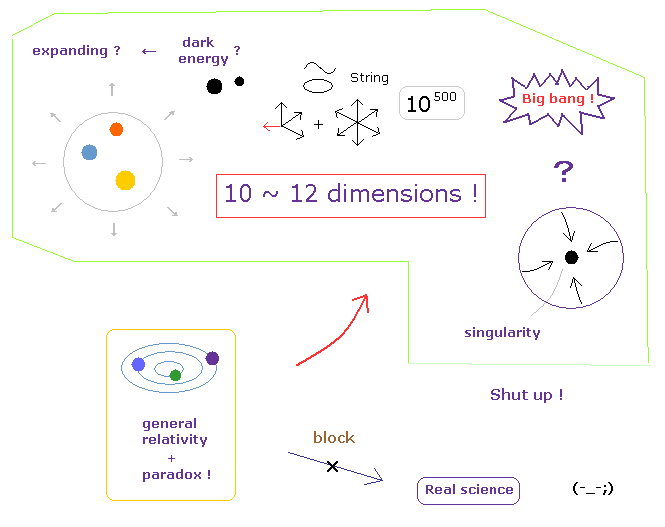
重力波は "質量"の加速度運動によって 曲がった時空間を伝播する さざ波 である。
もし重い星が 重力波を放射してれば その軌道半径が 縮んで その軌道周期が 時間とともに短くなる。
しかし Fig.2 で述べたように、この中性子星は 地球から 何と 21000 光年ものかなたにあると予測され、光の非常に長い道筋上での 様々な影響を 正確に予測することは はっきり言って不可能である。
この不確定性に加えて 実は 重力波自体 一般相対論に従って いないのである。
なぜなら 後で説明するが 重力波を表す "テンソル" は 真のテンソルに なり得ないからである。
さらに 重力波を得るには 人為的に 座標変換を制限しなければならない (= TT ゲージ )。
また 一般相対論が正しいとすると ( 致命的なパラドックスを無視して )、 非実在的な 10-12 次元の 超弦 ( M, F ) 理論、超光速のインフレーション、 ブラックホールの特異点、 暗黒エネルギー (= 宇宙膨張のため エネルギー保存則を破る ) などのファンタジーを信じるしか他に道が残っていない。悲惨である。
(Fig.4) 重力波の検出 = 多大な時間と お金の無駄使い。
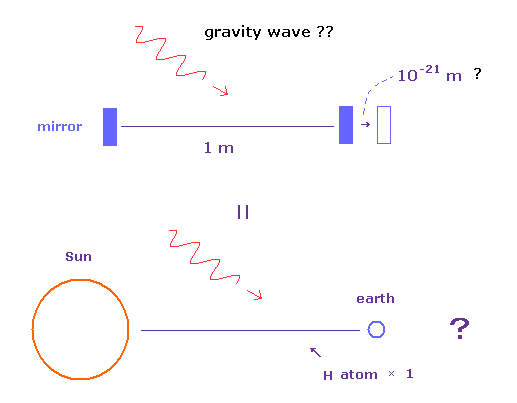
重力波は 非常に弱い。
彼らは 超新星などの波源からの重力波が 干渉計の腕の長さをわずかに変化させ、その変化を 光の干渉を用いて検出できるとしている。
しかし この腕の長さの変化量は 恐ろしく小さい。太陽と地球の間の距離でも わずか 水素原子1個分の長さぐらいが変わるだけのものである。
もちろん、良く分かっていない暗黒物質、暗黒エネルギー、真空の量子振動などの 無数のノイズも見分ける必要がある。
つまり 例え 将来 彼らが重力波を見つけたと主張したとしても、その結果は 非常に疑わしいことは言うまでもない。
彼らは 超巨大な干渉計の建設や 果ては 複数の人工衛星を利用した検出などに 莫大な時間と金を浪費しようとしている。
しかし 例え この非常にかすかな変化 (= 重力波の ? ) を観測したところで、ノイズとほとんど見分けがつかない 弱すぎる重力波が 実際に何かに役立つことは はっきり言って あり得ない。
(Fig.5) ボーア軌道の加速する電荷は放射しない = "質量" も 重力波を放射しない。
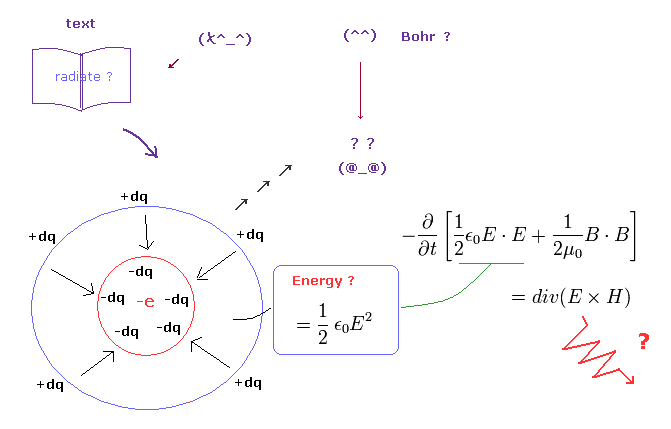
通常の教科書は よく古典的なボーア軌道の 加速する電子 は エネルギー放射して 核に落ちていくと述べている。
しかし 実は これらの説明は完全に間違いである。
また このメカニズムは 重力波の実在性に利用されるが 残念ながら 単一の電荷が 電磁波放射することはない。
この主張は ポインティングベクトル (= E × H ) を エネルギーの流れとして用いている。
この ポインティングベクトルは 真空における 電場、磁場のエネルギーの変化を表している。
この真空における電場エネルギー (= 1/2εE2 ) は ( Fig.5 左 ) に示すように 中心の導体球に マイナスもしくはプラスの無限小電荷を 集めるのに必要な ポテンシャルエネルギーを意味している。
しかし 単一電子は それより小さな電荷の集まりではない ( 単一電子は 最小の電荷である )。
これはつまり 真空の電場エネルギーは 単一電子においては エネルギーではないことになる。
すなわち ポインティングベクトルは 単一電子の場合は エネルギーの流れを意味していない。
( このページも参照のこと。 )
つまり これらの間違った説明は ボーア軌道に関する 一種の "マインドコントロール" のような役目を果たしていると考えられる。
(Fig.6) 観測者の加速度運動が 電磁波放射や 重力波をキャンセル ??
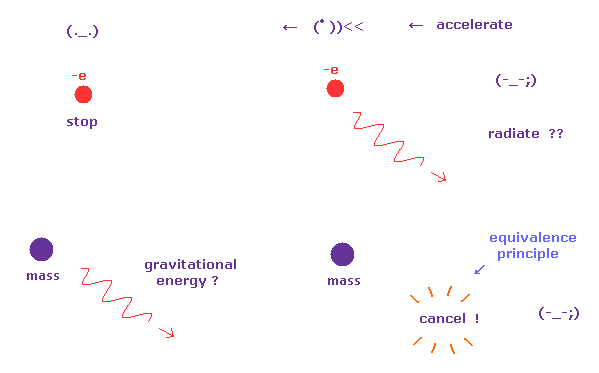
単一の加速度運動する電荷が エネルギー放射し、かつ 等価原理が正しいとしたら、非常に 奇妙な現象を受け入れなければならない。
左上の図では 単一の電荷が静止しており、エネルギー放射していない。
しかし ある観測者が加速度運動し始めると、観測者の視点からは 荷電粒子が加速度運動していることに等しいから エネルギー放射し始めてしまう。
つまり この電荷のエネルギー放射の是非は 何の関係もない 観測者の動きに応じて決まることになり、明らかなパラドックスである。
( この効果は ウンルー効果や ホーキング放射で使用されている。 )
同様に、ある加速度運動する "質量" が 重力波 (= エネルギー ) を放射すると仮定する。
等価原理によれば、ある観測者が加速度運動すれば、その地点で 重力場をキャンセルすることができ、すなわち重力エネルギーが 消えてしまい 保存されないことになってしまう。
(Fig.7) 重力波は エネルギー・運動量"テンソル"に矛盾する。

結果的に 重力波は 一般相対論の予測する エネルギー・運動量テンソルと矛盾しているのである。
つまり 重力波を表現するには 本当の "テンソル" を諦めなければならないのである ( → "擬テンソル" )。
( 実際に このことに関して 長いこと激しい論争があった。 )
これは明らかに自己矛盾と言える。
(Eq.1) 共変微分 (= テンソル ) と通常の微分 (= テンソルでない )。

表記法は このページと同じである。
このページでのみ "c" を最初に省いて 後でそれを戻す。
特殊相対論と異なり、通常の微分は 共変ベクトルにならない。
( ベクトルとは 座標変換のもとで 4元ベクトルとして変化するという意味である。 )
Eq.1 に示すように、共変微分は 非常に複雑な クリストッフェル記号 (= Γ ) を含んでおり、この部分が 一般相対論の場の量子化の際に 深刻な発散を引き起こす。
このため 非現実的な超ひも理論が この問題の解決のために導入された。
このページでは 通常の微分を "," と表記し、共変ベクトルを Eq.1 に示すように ";" と表記する。
(Eq.2) 弱い重力場での近似。
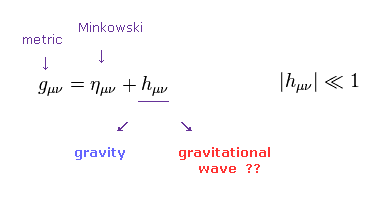
重力波を得るには 弱い重力場の近似などに頼る必要がある。
Eq.2 に示すように、一般化された計量テンソル (= g ) は 通常のミンコフスキーのテンソル (= η ) と 重力場のテンソル (= h ) に分離できる。
非常に弱い重力のため, この "h" は 非常に小さいとする。
( 厳密に言えば、この "h" は 重力波を得るのに 真の "テンソル" にはなれない。 )
(Eq.3)
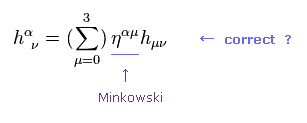
"h" は テンソルを意味していないにも関わらず、彼らは 近似的に ミンコフスキーのテンソル η を "h" の添え字の上下移動に用いている。
これも変である。
(Eq.4) クリストッフェル記号 Γ の近似。
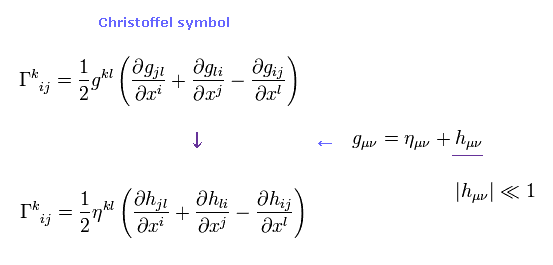
2次の "h" の効果を無視して、クリストッフェル記号は Eq.4 のようになる。
(Eq.5) bar-h のローレンツゲージ条件 = "人為的な" 制限。
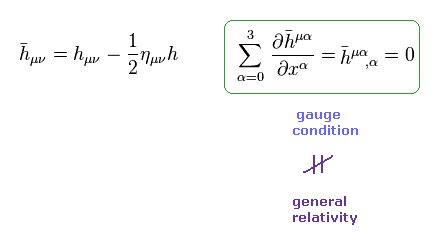
ここで Eq.5 のように bar-h というものを定義して、それが ローレンツゲージ条件を満たすと仮定した。
この計量テンソル h を ある条件に
制限することは この理論が 通常の一般相対論に 該当しないことを意味する。なぜなら この条件によって 任意の座標変換が禁止されるからである。
再び 厳密に言えば 重力波は 一般相対論と等価ではない。
(Eq.6) 座標変換の制限。
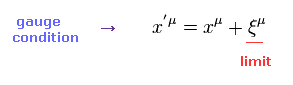
Eq.5 の特殊な制限と、 Eq.2 と Eq.4 の近似を用いると、次のアインシュタインテンソル (= G ) を得る。
(Eq.7)
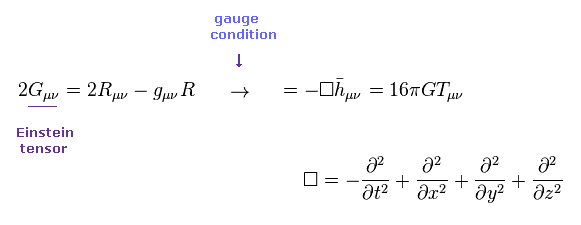
Eq.7 の解は
(Eq.8)
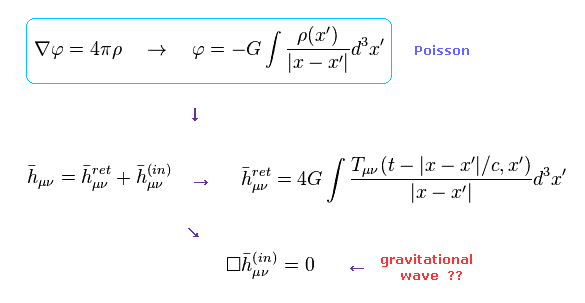
この解は 通常の重力場 (= 上 ) と、真空の重力場 (= 下 ) を含む。
Eq.8 の下の解が 重力波を表している。
(Eq.9)
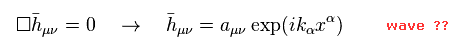
Eq.8 の平面波解 (= 下の重力波 ) は Eq.9 に示したようになる。
Eq.9 では、 "aμν" は テンソル形式の定数である。 ( 厳密にはテンソルではないが・・。 )
(Eq.10) TT ゲージ = 数学上のトリック 座標変換に人為的な制限。
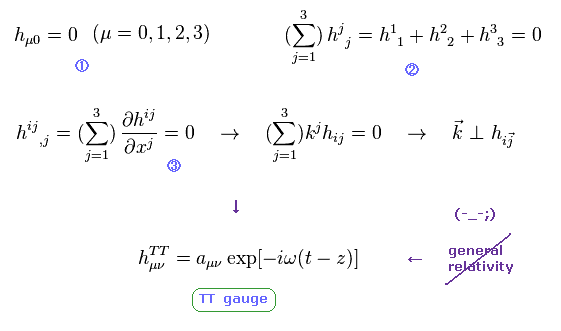
実は 重力波を得るには Eq.10 に示すような ある特殊な3つの条件に頼らなければならない。
Eq.10 の最初の条件では 重力波から 時間成分のテンソルを排除している。
2番目の条件は トレースレスの条件で 単なる人為的な定義にすぎない。
3番目が ローレンツゲージの条件である。
これら3つの条件を満足するために、任意の座標変換を諦めなければならないのである。
つまり TT ゲージは 一般相対論の基本的な原理に矛盾しているのである。
(Eq.11) トレースレス。
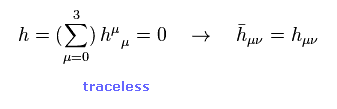
"h" の トレースレスは h = 0 の意味である。
つまり Eq.5 と Eq.11 より bar-h のテンソルが h に等しくなる。
この条件は 重力波を得るためのみに導入されたと言っていい。
(Eq.12) エネルギー保存 = 一般相対論に違反する。
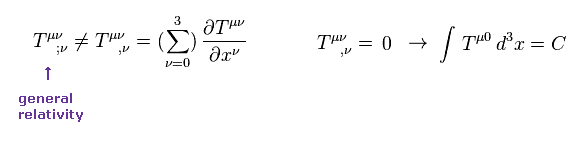
このページに示したように、一般相対論の エネルギー・運動量テンソルは 共変微分 ( 通常の微分でなく ) で表される。
しかし 重力波が ある空間に含まれるエネルギーを運ぶには 古典力学のような 通常の微分を用いる必要がある (= Eq.12 右 )。
Eq.12 右の積分は ある空間内での エネルギー保存則を意味している。
もし このエネルギーが保存されないと、パルサーからの重力波放射の効果を 正確に予測 できないことになる。
(Eq.13) その代り "テンソル" を諦めなければならない。

Eq.13 を見て分かるとおり、 通常の微分 (= , ) は 明らかに 共変微分 (= ; ) と 異なる。
Eq.13 (= ある空間内でのエネルギー保存則 ) を満たすためには 重力波が 真のテンソルにはなり得ないという 矛盾した事実を受け入れなければならない。
( 結果的に それは エネルギー・運動量擬テンソル" と呼ばれる。この人為的なルールをどう思われるだろうか? )
(Eq.14)
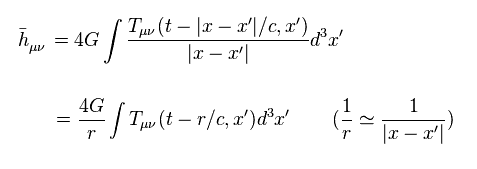
Eq.8 の解は Eq.14 のように書ける。
(Eq.15)
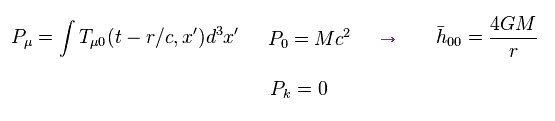
T00 成分 (= 時間-時間 ) のみが "質量" (エネルギー) を表す。
Pk (= 時間-空間 ) 成分は運動量を表し、ある重心系を選ぶと キャンセルすることができる。
(Eq.16)
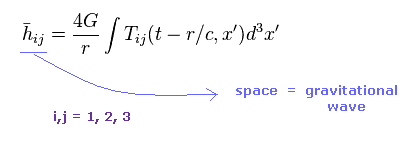
結果的に "h" の 空間-空間成分が 重力波を表していると 彼らは主張している。
(Eq.17)
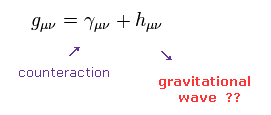
重力波を得るには 何らかの近似に頼らなければならない。
ここでは 簡潔に アイザックソンのエネルギー・運動量擬テンソルの近似式に触れる。
一般化された計量テンソルを Eq.17 のように "γ" と "h" に分離する。
この γ は 重力波からの 反作用を含むと仮定する。
(Eq.18)
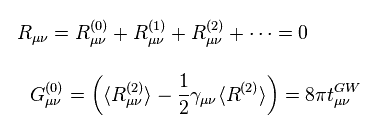
R2 は 計量 "h" の2次の近似を含む リッチテンソルの意味である。
長い計算の後、Eq.18 の 近似的なアインシュタインテンソルを得る。
(Eq.19)
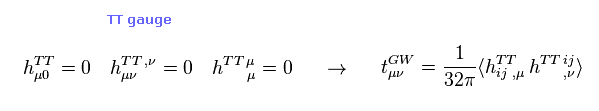
Eq.10 の TT ゲージ条件を用いて、 Eq.19 のエネルギー・運動量擬テンソルを得る。
これを "アイザックソンの式" と呼ぶ。
(Eq.20) ニュートンポテンシャル φ の展開。
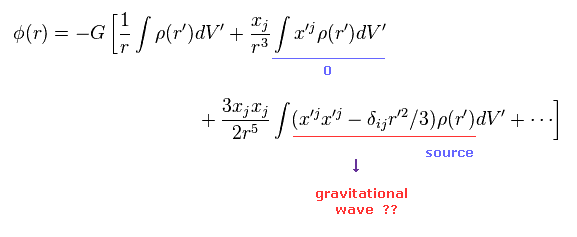
Eq.20 のように ニュートンポテンシャルを展開することができる。
右辺の 2項目 (= 双極子 ) は ある重心系を選ぶと ゼロにできる。
よって 電磁場とは異なり 重力波の源は 4重極モーメント (= 3項目 ) になる。
(Eq.21) 四重極モーメント Q.
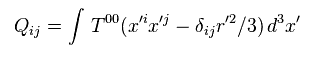
この 四重極モーメント Q を用いて、重力波の擬テンソル (= Eq.19 ) は 次のように表せる。
(Eq.22)
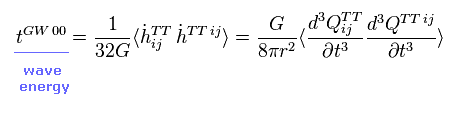
つまり 波源の "質量" は 重力波を放射するのに加速度運動する必要がある。
(Eq.23) 射影演算子
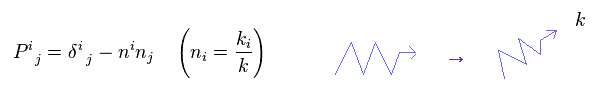
ある重力波を 任意の方向へ向けるには Eq.23 の射影演算子を用いる。
"k" は 重力波の 波数ベクトルである。
(Eq.24)
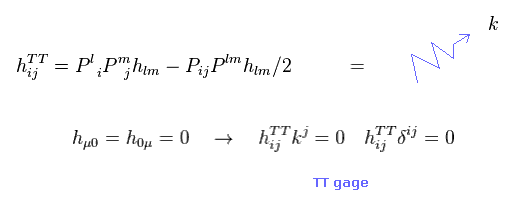
ベクトル "k" の方向へ進む 重力波の擬テンソル "h" は Eq.24 のように表せる。
この擬テンソル "h" は 必ず TT ゲージ条件を満足することになる。
つまり この複雑な数学公式は この人為的な条件のためだけに 導入されたと言っていい。
(Eq.25) 単位時間あたりの 重力エネルギー放射。
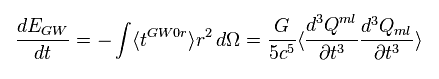
射影演算子を用いて、Eq.21 のテンソル Q を 動径方向へ向ける。
それから ある球面上で積分する。
この結果が Eq.25 である。
これが 単位時間あたりに放射される 重力波のエネルギーである。
(Eq.26) 2つの質量 (= m ) が x = ± a に位置する。
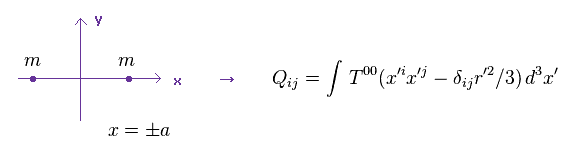
中性子星の連星系から放射される重力波を計算するには 最初に Eq.26 の状況を設定する。
Eq.26 では、 質量 "m" を持つ 2つの物体が "x" 軸上 ( x = ±a ) に存在する。
(Eq.27) 空間-空間 擬テンソル。
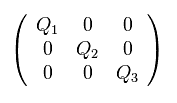
Eq.27 のような 空間-空間 擬テンソルを仮定する。
Eq.26 (= 2 × m が x= ±a にある ) を Eq.21 に代入して、 次のような 4重極モーメント Q を得る。
(Eq.28) 四重極双極子。
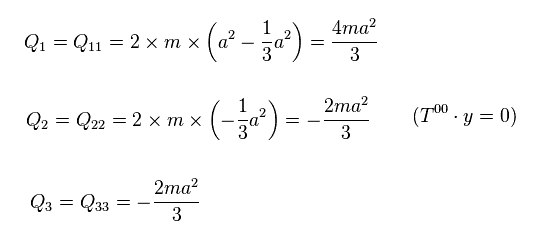
重力波を放射するには 加速度運動する必要がある。
これら2つの物体が x-y 平面上を 角速度 Ω で 回転している状況を考える。
(Eq.29) x-y 平面上での回転。
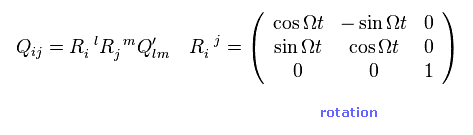
時間 "t" 経過後、 この 4重極 Q (= 擬テンソル ) は Eq.29 のように変化する。
(Eq.30) テンソルの変換 = スピン 2 ?
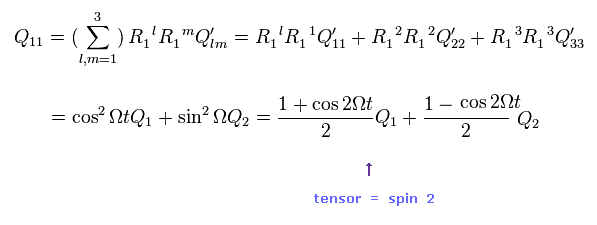
Eq.30 は Q11 成分の変換を表している。
見てのとおり、 この Q は 元の回転の振動数の2倍の 2Ω の角振動数で変化していることがわかる。
これは テンソルの変換 (= R × 2 ) を用いたことに起因する。
だから 彼らは 重力子は スピン "2" であると主張しているのである。
しかし ご覧のとおり このスピン自体に 物理的実態は何もなく、単なる抽象的な "数式" にすぎない。
(Eq.31) すべての成分の結果。
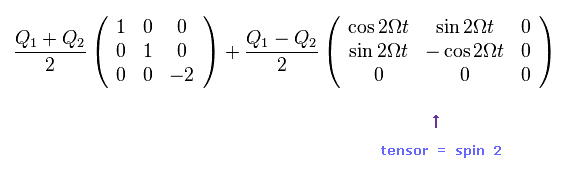
Eq.31 の結果を Eq.25 に代入して 次を得る。
(Eq.32) 中性子星から放射される重力波。
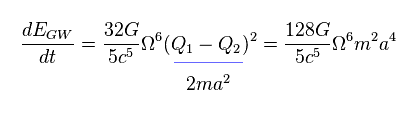
Eq.32 は 単位時間ごとに 中性子星 連星系から放射される 重力波のエネルギーを表している。
Eq.32 の関係式を用いて、 パルサーの軌道周期の変化を求めることができる。
もちろん、この軌道周期を出すには 連星系の2つの質量 (= m1、 m2 ), 振動数 (= Ω )、軌道半径 (= a ) などの関連するパラメーターをすべて あらかじめ出しておく必要がある。
さらに パルサー 1913+16 は 地球から 何と 21000 光年ものかなたにあるため、電磁波が その長〜い道中に受ける非特異的な無数の変化と 元のわずかな変化を見極めることは はっきり言って 不可能である。
(Fig.7) "21000" 光年も離れている → 非常に疑わしいデータ解釈。


2013/10/23 updated This site is link free.