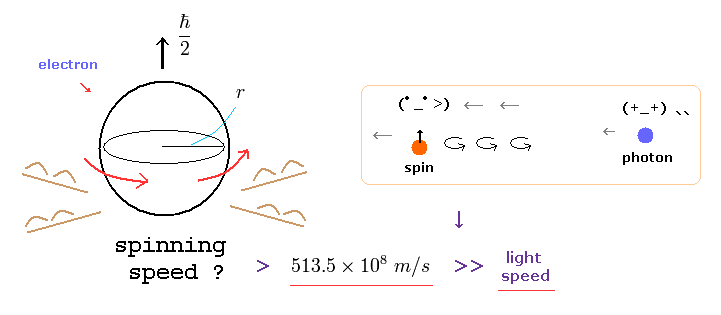
トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは実在しない。
近藤効果は "スピン" とは関係ない。
BCS理論は 計算間違いをしている。
(Fig.1) 電子のスピン回転速度は 光速を はるかに超えている。
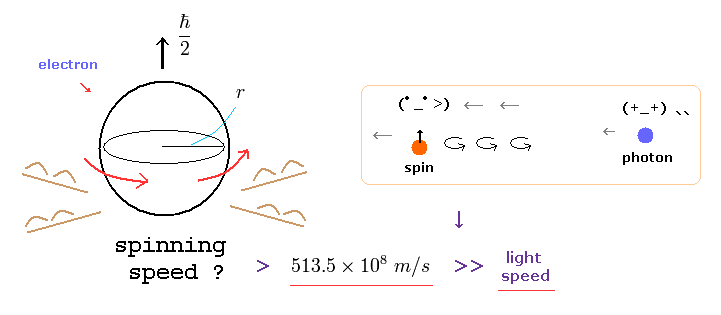
実際の実験によれば、単一の電子は 点状粒子のように 非常に小さい。
しかし 量子力学は この点状の電子は 1/2 ħ の角運動量を持っていると主張している。
ご存じの通り、角運動量は mv× r である ( m= 電子質量、 v=回転スピード、 r =電子の半径 )。
電子の 非常に小さな質量と半径を考慮すると、この回転スピードは
光速の 100 倍以上にならないと 1/2 ħ の角運動量に到達しない ( このページも参照のこと )。
これはつまり 量子力学のスピンは 非現実的で かつ 想像上の産物であることを示している。
(Fig.2) フェルミ粒子は 360°の回転で 元に戻れない。
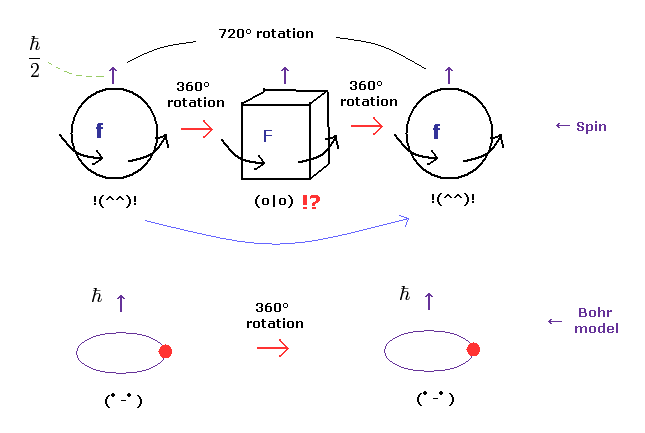
奇妙なことに、非現実的な量子力学によれば、電子、中性子、陽子などの すべてのフェルミ粒子は 360°回転で 元に戻れないのである。
なぜなら これらの粒子は スピン角運動量の 1/2ħ を持っているからである。
もちろん、この角運動量が ボーア軌道のように ħ の整数倍だとしたら、それは 360°回転で 元に戻ることができる。
( これは 当たり前の話である。 )
驚くべきことに、 このページに示したように、この架空の現象が 実際の実験で確かめられたと 彼らは主張している。
重要な点は これらの実験は フェルミ粒子の角運動量が 1/2 ħ であるという 前提条件で行われている点である。
もし この一方的な仮定を止めて、それらが ħ の角運動量を持つとすると、これらの実験は 単に 粒子が 360°回転で 元に戻ったという 当たり前の結果を示しただけになる。
つまり これらの実験は 明らかに スピンの角運動量 1/2 ħ が 間違いで ファンタジーであることを示している。
(Fig.3) ボーア軌道 (= ボーア磁子 ) = 電子スピン (= ボーア磁子 ) ?
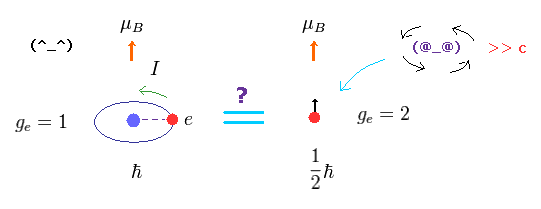
このページに示したように、ボーア軌道の基底状態の磁気モーメントは ボーア磁子である。
驚くべきことに、電子スピンの磁気モーメントも このボーア磁子なのである。
( スピンは ボーア軌道とは 何の関係もないのにである。 )
なぜなら 量子力学の水素原子の基底状態は 角運動量を 持っておらず、代わりに このスピンを持つからである。
この水素の磁気モーメントの実験値は ボーア軌道から得られた ボーア磁子とちょうど同じである。
そのため 彼らは もし電子スピンもボーア磁子を持つとしたら、実験値に合うと主張し始めた。
それだけの理由である。
(Fig.4) 奇妙な "スピン" が間違っていたら、ほぼすべての理論が崩壊する。
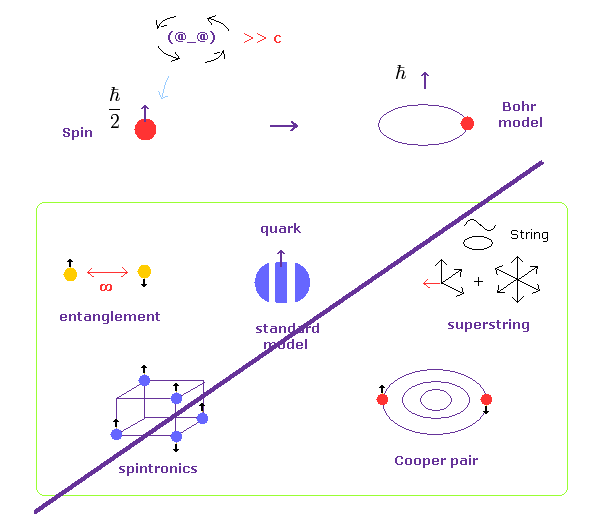
奇妙なスピンは 非常に非現実的で 理不尽であるが、 トップジャーナルや研究者達は 決して このスピンを諦めようとしない。かつ 決して スピンとは何かを問おうとしない。
なぜなら もし このスピンが 間違っていて それが通常の古典的な円軌道だとしたら、エンタングルメント、標準模型、超ひも理論、スピントロニクス、クーパー対などの すべての理論が 崩壊してしまうからである。
つまり実は この単なる数学上の”スピン”は 現在世界に存在するフィクションの中で
最も影響力のある概念なのである。
もちろん これらの理論はすべて 非現実的で 問題だらけということを考慮すれば、 本当の科学の発展のためにも これらすべての概念を書きなおして 先に進むべきである。
非常に簡単なことである。ただ スピンとは実際 何なのか 問うことをスタートさせればいいだけである。
(Fig.5) スピン・スピン相互作用は幻想である。
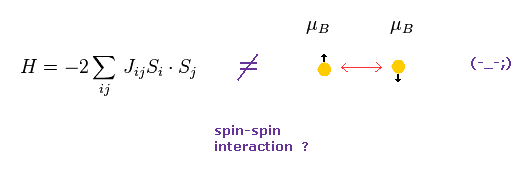
現在の物性物理学では、強磁性、反磁性を表すのに Fig.5 の関係式が よく使われる。
Fig.5 で 交換相互作用定数 J が 正のとき、平行なスピンが エネルギーを負にして安定にする (= 強磁性 )。
そのため 彼らは 強磁性においては 1つのスピンが 他のスピンに影響を与えるとしている。
しかし もしこのスピンが "磁気モーメント" (= ボーア磁子 ) だとしたら この強磁性自体不可能である。
(Fig.6) スピン・スピン相互作用は 非現実的なぐらい弱い。
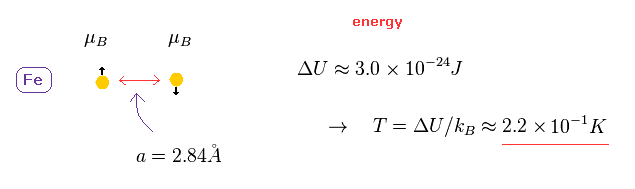
鉄の格子定数は 2.84 Å である。
この距離では スピンが平行、反平行の状態の間のエネルギー差は Fig.6 に示したように
非常に小さい。
ボルツマン定数 k を用いれば、このエネルギー差は たったの 0.22 ケルビンである。( 付録も参照のこと。 )
そのため スピン・スピン相互作用が それらの磁気モーメントによって生じるとしたら、磁石は 室温で 簡単に壊れてしまうことになる。
この本 ( スピンはめぐる。朝永著 ) によれば、一重項と三重項スペクトルのエネルギー差は 非常に弱い スピン・スピン相互作用だけでは説明できない。
なぜなら スピン・スピン相互作用は弱すぎるからである (= 微細構造の 約 0.00005 eV レベル。 このページも参照のこと。 )
つまり 彼らは 単に 何らかのクーロンエネルギー状態間の差を スピン・スピン相互作用という名に置き換えただけなのである。
( 公式には これらのエネルギー差は 波動関数の "対称性"、"反対称性" によって生じるとされている。)
(Fig.7) 本当のスピンの状態 ? 点粒子?
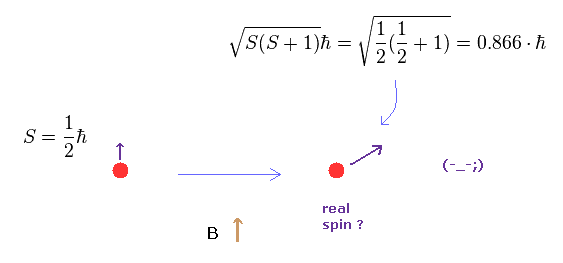
スピントロニクスや 物性物理学では、Fig.7 の関係式を頻繁に使用する。
つまり 量子力学によれば、"本当の"スピンの角運動量は 1/2 ħ ではないのである。
奇妙なことに、彼らが言うには 点状粒子であるスピンは 歳差運動しており、ほとんど 磁場 B とは 異なる方向へ スピンが 傾いていることになっている。
Fig.7 のスピンの関係式は 通常の軌道角運動量 L と異なり シュレディンガーの水素原子から得られたものではない。
また 異なった様々な磁場中においても どうして このスピンの傾き角度が 常に一定で不変なのかを 彼らは決して説明しようとしない。
このミステリアスな 傾きの起源は 21 世紀になった今でさえ 謎のままである。
奇妙としか言いようがない。
(Fig.8) スピンの証拠 ?
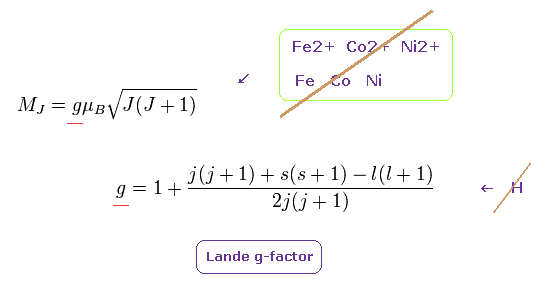
このページに示したように 込み入ったランデのg因子は 主に ナトリウムの異常ゼーマン効果から得られたものである。
最初に このランデのg因子は 一番単純な 水素原子に 適用できない。
なぜなら ランデがこの関係式を導入したとき、スピンという概念はまったくなく、S は 内殻の
芯部分の電子によるものだ とされていたからである。
さらに このランデのg因子は Fe, Co, Ni, Fe2+, Co2+, Ni2+, Sm... などの重要な金属やイオンに まったく適用できない。
(Fig.9) 角運動量ゼロ ?
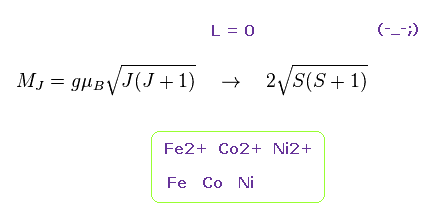
ランデのg因子を実験値に合せるために、彼らは Fe2+, Co2+, Ni2+ などの 3d 軌道の 角運動量を 人為的に削除してしまった ( L=0 )。
彼らが言うには これらのイオンの 3d 電子は 自由に飛び交っており、原子核に束縛されていないため それらの角運動量はゼロに近くなるらしい。
しかし この解釈は はっきり言ってまったく不合理の極みである。
なぜなら 3d 軌道というのは 非常に大きな角運動量を持っており、かつ すでに +2 の正イオンになっている金属から さらに 3d 電子が自由に遊離するということは 常識的にあり得ない ( Fe2+ が Fe4+, Fe5+ .. などになってしまう。)
これらの操作は 明らかに 実験結果に合致するための 意図的なものであることは明白である。
さらに Fe, Co, Ni, Pm, Sm .. などの原子は これらの操作をした後でさえ ランデのg因子が 実験結果と合致しない。
そのため 彼らは 他の原子が関与した 何らかの 別のスピン・軌道相互作用などを 複雑に組みこんで その食い違いを説明しようとしている。
見てのとおり、現在のスピントロニクスは 様々な人為的な操作によって 実験値に無理やり 合わせようという行為の集合体の結果なのである。
(Fig.10) これらの軌道を 実際に見ることはできない。
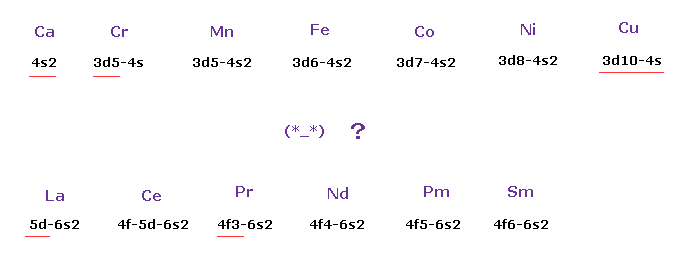
Fig.8 に示したように、このランデのg因子は 様々な軌道形態 ( s, p, d, s, .. ) の値に 完全に 依存している。
例えば K や Ca の原子では、電子は最初に 4s 軌道に入る。
その後の原子では、電子は 下の 3d 軌道に入ることになっているが その 本当のメカニズムは 不明のままである。
ランタノイドでは、軌道形態は La で 5d-6s2、Ce で 4f-5d-6s2、 Pr で 4f3-6s2 となっており、複雑極まりない。
重要な点は これらの軌道を 実際の実験で 確かめることが できないということである。
なぜなら 配位結合などで これらの架空の軌道は 混合して sp2、sp3 などのような 別のものに変化してしまうからである。
つまり 様々なスペクトラムに合うように これらの軌道を 人為的に定義することが可能なのである。
(Fig.11) 角運動量ゼロ (= s 軌道 ) → 外殻電子が 内殻を貫通??
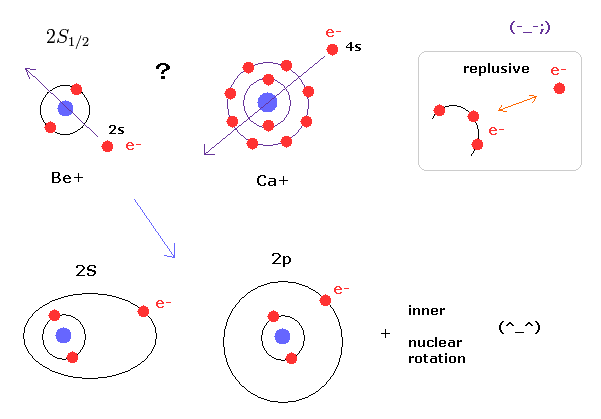
何度も言っているように、 ゼロ の角運動量 ( L=0 ) の "s" 軌道というのは 現実的な原子構造においては 絶対に あり得ないものである。
なぜなら 電子は 強いクーロン反発力のため 内殻の電子群を貫くことができないからである。
この奇妙なゼロの角運動量を認める代わりに、外殻の電子が 内殻の電子群の周囲を周っていると考えたほうが 極めて自然である。
もし楕円もしくは円軌道を考慮すれば、2s と 2p のエネルギー準位差を説明することができるし、また このページに示したように、 ディラックの水素原子は 根本的に 間違った軌道を含んでいる。
(Fig.12) 3d 軌道は 非常に疑わしい。

Fig.12 に示したように、第一イオン化エネルギーは P → S → Cl → Ar の原子において 徐々に上昇していく。
そして カリウム (K) で このイオン化エネルギーは 突然 がくっと下がる (= 4.3 eV )。つまり この K から 別の軌道がスタートしたことが分かる。
4s と 3d の入り混じった軌道においては このイオン化エネルギーは 非常に滑らかに上昇していっている。 ( 4.3 → 6.1 → 6.5 → 6.8 .. )
これらのイオン化エネルギーの変化を考慮すれば、4s と 3d 軌道というのは 元から同じ "n" のエネルギー準位に属していると考えるのが自然である。
つまり この "3d" という定義は 非常に不自然なのである。
実際に、 V4+, V3+, V2+, Cr3+ ... などの磁気モーメントを得るとき、 彼らは 人為的に ランデのg因子を無視して 角運動量をゼロ にしてしまう。それらは 3d 軌道を含んでいるにも関わらずである。
これらの磁気モーメントは おおよそ 2 (= V4+), 3 (= V3+ ), 4 (= Cr3+ ), 5 (= Cr2+ ) × ボーア磁子である。
(Fig.13) 何が 強磁性を生じさせるのか?
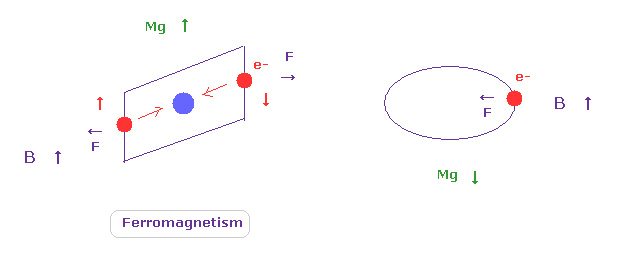
非現実的な量子力学においても 古典的なローレンツ力が 重要なことは言うまでもない。
Fig.13 左に示したように、外殻の電子が緩く原子核に結合した状態では それらの磁気モーメントは 外部の磁場 (= B ) と 同じ方向を向く。
重要な点は 強磁性を示すこれらの物質は規則的に配列された結晶でなければならないということである。
ほとんどの物質や分子では 各電子 (軌道) の磁気モーメントは様々な方向を 向いているため 互いにキャンセルし合って 反磁性の性質になる。
もちろん、結晶構造のために ドブロイ波も 互いに同調し合うことになる。
なぜなら トップページのヘリウムに示したように、磁場というのは 電子の運動による ドブロイ波によって生じると考えるのが自然だからである。
超伝導体では 完全な自由電子とローレンツ力のため Fig.13 右に示した 完全反磁性の性質を示す。
(Eq.1) "フォノン" って何? → 黙って計算だけしてろ !
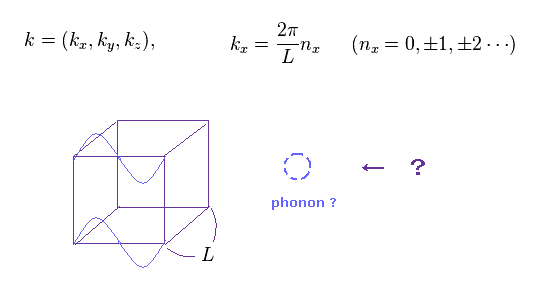
物性物理学では 非常に曖昧なフォノンという概念を頻繁に使用する。
一辺 L の 立方体と その周記境界条件を満たす 波長を考慮するとき、彼らは Eq.1 の関係式を仮定する。
(Eq.2) フォノンは "ドブロイ波"を意味している。
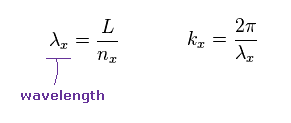
ここで λ は フォノンの波長、 k は 波数である。
これらの関係式は 曖昧なフォノンというものが
本当の ドブロイ波に類するものであることを示唆している。
つまり 物性物理学では 彼らは 暗黙のうちに 何らかのドブロイ波に 依存しているのである。
(Eq.3) 振動モードの数。
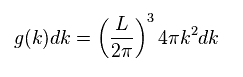
Eq.3 に示すように 波数 k 近くの球殻に含まれる 振動モードの総数を得ることができる。
この関係式は 物性物理学の 格子模型で 頻繁に使用される。
マイスナー効果によれば、超伝導体内の磁場は ゼロになる。
これらの効果は ロンドン等によって 通常の 古典的なマクスウェル理論を用いて説明された。
(Eq.4)
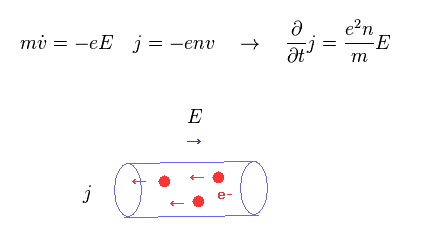
Eq.4 では、電子の密度は "n" で、電子の速度は "v" である。
外電場 E の下で、動く電子 (= 電流密度 "j" ) は 加速される。
(Eq.5) ロンドン方程式 = 反磁性。
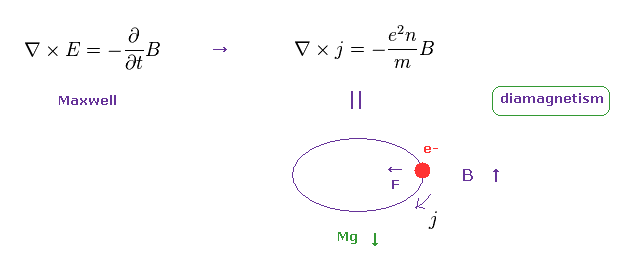
Eq.4 と Eq.5 (= ファラディーの法則 ) を用いて、 超伝導の 完全反磁性を示すロンドン方程式を得ることができた。
なぜなら ファラディーの法則によれば、動いている電荷は 古典的なローレンツ力によって 外電場を キャンセルさせようとするからである。
(Eq.6) 他の マクスウェル方程式。
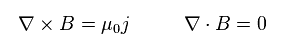
ここで Eq.6 の他のマクスウェル方程式を用いる。
上の式をすべて合わせて 次の式を得る。
(Eq.7)
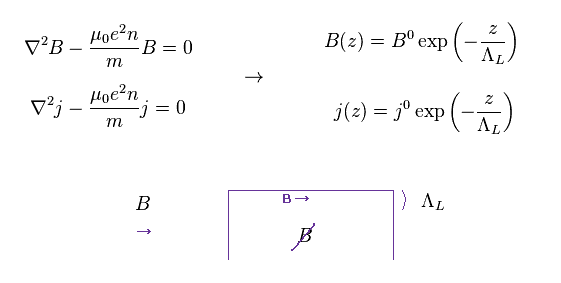
ここでは
(Eq.8)
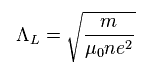
ΛL は ロンドン侵入長であり、外磁場が どれだけ超伝導体内に 侵入できるかを表したものである。
つまり 外磁場は 超伝導体内では 減衰してなくなってしまうことになる。
ファラディーの法則と マクスウェルの式に見られるように、マイスナー効果は 完全に 古典的な電磁気学によるものである。
(Fig.14) "クーパー対" は 本当に 実在するの?
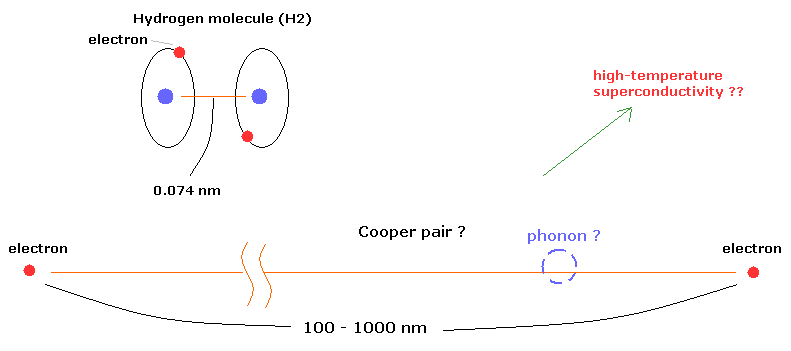
現在の物性物理学によれば、クーパー対は 低温状態において 非常に曖昧な存在である "フォノン" というものを介して結合するとされている。
驚くことに クーパー対の2つの電子間の距離は 何と 100 - 1000 nm (ナノメーター) もあるのである。
例えば、水素分子 (H2) の 核間距離は 約 0.073 nm である。
どうやって、これら2つの電子は クーロン反発力に打ち勝って 超伝導体の中で 安定して結合できるのだろうか?非常に奇妙である。
重要な点は 彼らが導入したフォノンというのは 非常に 人為的な概念だという点である。
また これらの フォノンは 単に "数学上"の概念 ( リアルな粒子でなく ) であるため、現在の BCS 理論は この 自ら設けた数学上の制限から逃れて 理論を発展させることができない。( このページも参照のこと。 )
(Eq.9)
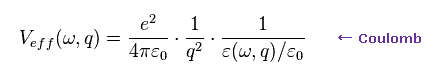
ここでは 簡単に これらの フォノンが 非常に 人為的で 単に数学上 ( 物理でなく ) の概念であるかを 簡潔に説明する。
Eq.9 は 2つの電子間の クーロン反発力のフーリエ成分である。
彼らは 次のように フォノンによる引力を生じさせるために 意図的に 誘電率 (= ε ) を 改変してしまった。
(Eq.10)
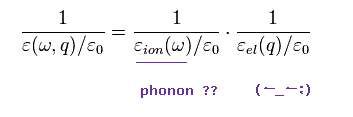
ここで 彼らは 強引に次のような関係式を定義した。
(Eq.11)
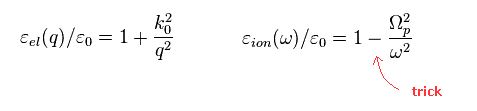
Eq.11 では、負の符号が フォノンによる引力を生じさせるポイントである。
奇妙なことに、Eq.11 では Ωp が フォノンの角振動数を表すと 彼らは主張しているのである。
しかし こういった 何の説明もなしに 天下り的に 非常に曖昧なフォノンを 引力を生じさせるために導入する手法は 理不尽極まりない。
(Eq.12)

Eq.10 と Eq.11 を Eq.9 に代入して、 Eq.12 を得る。
Eq.12 では、 電子のエネルギー ( ħω ) が 架空のフォノンのエネルギー (= ħΩ ) 以下のとき、このクーロン反発力は 引力に 変わってしまうのである。
あなたがたの感じられたように、2つの電子間 (= クーパー対 ) の引力は 何の断りもなしに突然 導入されたものである。
つまり これらクーパー対やフォノンというのは 単なる 想像上の概念であり、奇妙な "スピン" の証明には まったく ならないのである。
ここでは 磁束量子というのが 実在のドブロイ波によって生じ、クーパー対を意味しないことを示す。
なぜなら フォノン自身は 架空の準粒子であり、2つの電子間の引力は 非常に不自然だからである。
(Fig.15)
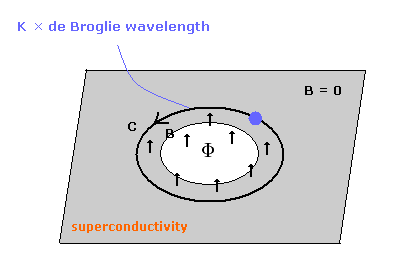
磁束量子 (Φ0) は 超電導体を通過する 量子化された磁束である。
この磁束は 次の量子化された単位の整数倍であることが 知られている。
( つまり Φ = Φ0 × 整数 )。
(Eq.13)
最初に シュレディンガー方程式を使って Eq.13 を求めることにする。
シュレディンガー方程式で Eq.13 を得るには、2つの電子からなる "クーパー対(ペア)" を想定しなければならない。
超低温の超電導体では Eq.14 に示すように すべての電子の 位相がそろう傾向にある。
残念ながら 彼らは、この電子の位相が何なのかということに まったく答えようとしない。
(Eq.14) 超電導体における波動関数。
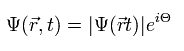
ここでは 位相 (Θ) は 次のように 運動量 (p) と エネルギー (E) から成る。
(Eq.15)
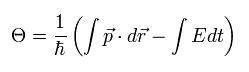
もし 2つの電子間の 反発力を忘れて ”クーパー対 ( -2e )” を仮定すれば、運動量 (p) と エネルギー (E) は次のようになる。
(Eq.16)
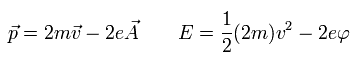
ここでは ローレンツ力 を考慮して 磁気ポテンシャル (= A ) と 電気ポテンシャル (= φ ) を用いている。
この置き換えに関しては このページも参照のこと。
空間部分のみに注目すると、Eq.15 は、
(Eq.17)
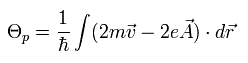
Fig.15 の穴の周囲を一周して、波動関数の位相が元に戻ることを考慮すると、
(Eq.18)
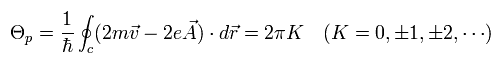
ここで K は 整数である。
マイスナー効果によれば、超電導体における 磁場や電流は無視できる。
そのため、Eq.18 の 電子の速度 (= v ) をゼロにすることができる。
(Eq.19)

ここで、 Φ は 磁束を意味しており、マクスウェルの法則によれば ベクトルポテンシャル (= A ) に囲まれたものである。
( B = ∇ × A. Φ = BS. )
Eq.19 から、穴の部分の磁束密度 (Φ) は 次のように 量子化される。
(Eq.20)

"K" は ある整数である。
ここでは 次の 磁束量子の単位を定義できる。
(Eq.21)
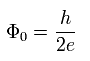
Eq.21 は "磁束量子 (Wb)" と呼ばれるものである。
そのため 彼らは クーパー対が 磁束量子を説明できるとしている。
しかし 例えば Eq.14 の 波の位相というものが何なのかなど 肝心な部分は まったく説明してくれない。
( もちろん お気づきのとおり、これらの位相は 実在のドブロイ波に関係していることは明らかである。)
(Fig.16) ドブロイ波長の整数倍。
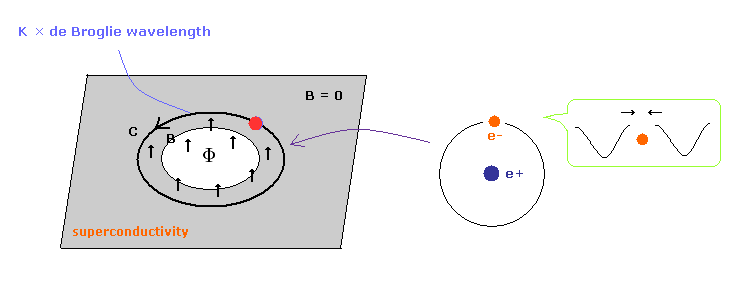
ここで 電子が Fig.16 の穴の周囲近くを 磁場をキャンセルさせるために回っていると仮定する。
遠心力が ローレンツ力に等しいことより、
(Eq.22)
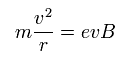
その軌道1周が ドブロイ波長の整数倍 (= K ) に等しいとき、
(Eq.23)
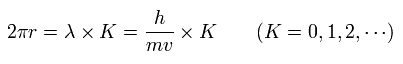
ここでは λ = h/mv。
Eq.22 と Eq.23 から、次を得る。
(Eq.24)
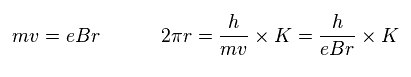
そのため
(Eq.25)
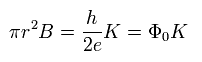
Eq.25 は Fig.16 の穴を通過する 磁束 (Φ) である。
( πr2 は この穴の面積である。 )
結果的に "実在の"ドブロイ波を用いて 超電導の磁束量子を得ることができた。
(Eq.26) = Eq.21
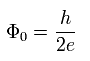
また ここでは クーパー対は必要ない。
もちろん、クーパー対が存在しなければ、高温超電導のような問題も 最初から存在しない。
( 彼らは この問題を ひも理論の共形場理論を用いて解決しようとしているが、この手法には 何のリアリティーもない。 )
このドブロイ波の位相は 量子トンネル効果や ジョセフソン効果と関係している。
そのため 量子トンネル効果は ファンタジーの量子力学でなく 実在のドブロイ波によって生じていると言える。
(Fig.17)
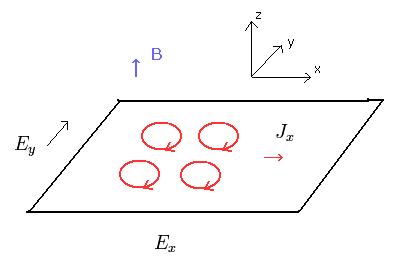
量子ホール効果では、電子は 外電磁場と垂直の方向へ動いている。
このページに示したように、分数量子ホール効果も含めて実在のドブロイ波によって説明可能である。
(Fig.18) 伝導率 ( 電流 ) は 量子化されている。
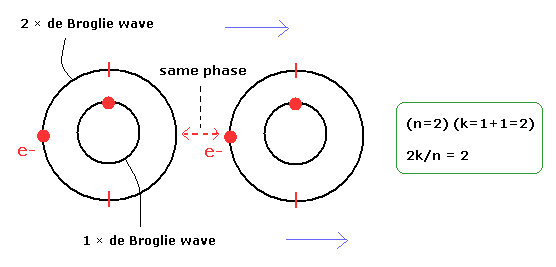
量子ホール効果では、伝導率 ( と電流 ) は 量子化されている。
電子のドブロイ波を考慮すれば、それらの波の位相が これらの効果に関係していることは明白である。
(Fig.19) どうして 奇妙な分数電荷が 2次元系でのみ出現するの?
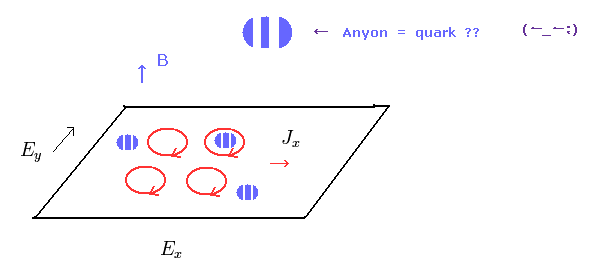
分数量子ホール効果の本当のメカニズムは 不明のままである。
ある理論では、非常に奇妙な粒子"エニオン" を導入して説明しようとしている。
エニオンは ボソンでも フェルミ粒子でもない。
さらに これらのエニオンは 何と 分数電荷を持つのである。あり得ない話である。
お気づきのとおり、現在の量子力学は 単なる ファンタジーと化しつつある。
( 最初からであるが・・。)
(Fig.20) スピンホール効果 ? 本当に "スピン" ?
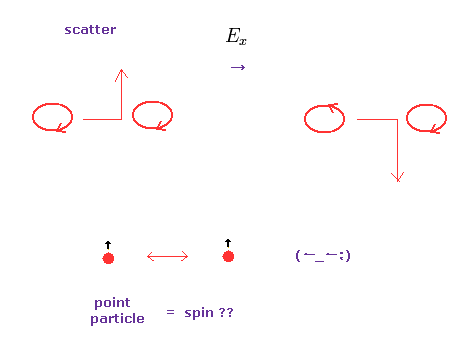
スピンホール効果は 通常の量子ホール効果と まったく異なる概念である。
移動する電子が それらの磁気モーメントの方向 ( up もしくは down ) に応じて 電場 ( 磁場でなく ) に垂直な方向へ移動する。 .
粒子間の何らかの "衝突" が この効果に関係しているとされている。
この効果は 通常のホール効果に比べて 各段に弱く、検出が難しい。
かれらは これらの磁気モーメントが "スピン" によって生じるとしている。
しかし 電子が 点状粒子であるにも関わらず どうやって それらの向きを区別することができるのだろうか? 不可能である。
それに 非常に小さな点粒子同士が 互いに都合よく衝突すること自体不自然である。
何らかの軌道運動 (= ドブロイ波 ) の方向の違いが この効果を生じさせると考えるのが 自然である。
(Fig.21) スピン・磁気相互作用は 幻想である。
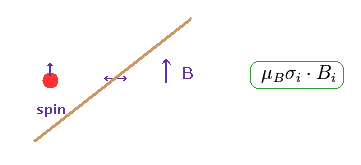
量子力学では、スピン・軌道相互作用は ディラック方程式と電磁気相互作用から得られる。
実は この計算過程において 彼らは 一種の "数学上"のトリックを使用している。
彼らは 人為的に 電子のドブロイ波を 外磁場に 変えてしまったのである。
もともと 電子の ドブロイ波は 外磁場とは 何の関係もないのにである。
ここでは このトリックについて 簡単に説明する。
(Fig.22) ローレンツ力 → 演算子の置き換え。
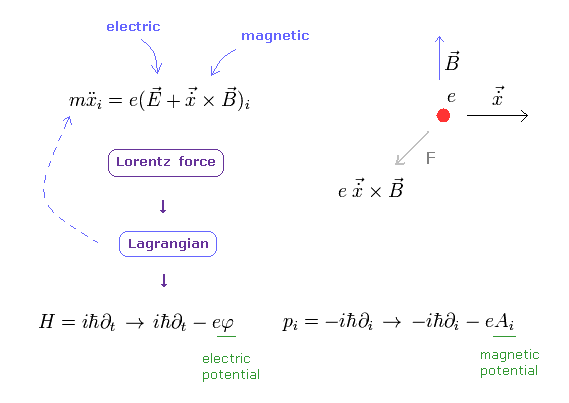
量子力学や 量子電磁気学 (QED) の 電磁気相互作用は 完全に 古典的な ローレンツ力に依存している。
このページに示したように まず ローレンツ力を与える ラグランジアンを得る。
次に このラグランジアンを元に ハミルトニアン (= H ) を導出する。
この最後のハミルトニアンにおいて 磁気 (= A )、電気 (= φ ) ポテンシャルが 元の運動方程式に付け加えられている。
(Fig.23) 自由粒子の方程式 → A, φ ポテンシャルが加わる → スピン・磁気相互作用 ?

Fig.23 の最初の式は 自由粒子のハミルトニアンである。
σ は パウリ行列 (= スピン ) で、これは 最初の式では 隠れている。
2番目の式は Fig.22 の最後の行 (= 外電磁場 ) の 演算子の置き換えを使って得られる。
彼らは この計算において スピン・磁気相互作用項が得られたと主張している。
しかし 本当にそうだろうか?
( ここでは μB は "ボーア磁子" である。 )
(Fig.24) 電子のドブロイ波が 外磁場に変わっちゃった?
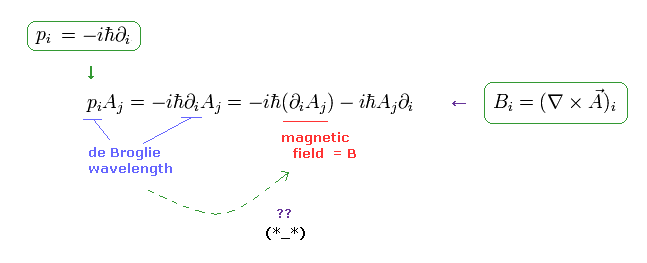
Fig.23 では、電子の 微分演算子 (= ドブロイ波 ) を 何と 外磁場の一部に転用してしまったのである。
磁場 B は ∇ × A (= 磁気ポテンシャル ) に等しい。
( この ∇ は もともとは 電子の "ドブロイ波" である。 )
もちろんのことだが、外磁場 B は 完全に この電子から 独立した存在であることは言うまでもない。
つまり 量子力学における このスピン磁気相互作用というのは 単なる "数学上"の技巧にすぎず 架空の存在であることを示している。
(Fig.25) スピン・軌道相互作用は 幻想である。
スピン・軌道相互作用も ディラック方程式から 近似的に得られる (= パウリ近似 )。
実は このスピン・軌道相互作用の強さは 実験値と比較すると とてつもなく弱いのである。
( つまり スピン・軌道相互作用というのは 現実のものではないのである。)
彼らは 金属の 何らかのバンド構造に起因する 別の強力な電気ポテンシャルが 関係している と主張しているが 非常に曖昧である。
現在の物性物理学は "現実的な"メガニズムから 逃れて 非常に曖昧な概念や説明に 逃げ込む傾向にある。
実際 彼らは まったくと言っていいほど これらの現象の 具体的なメカニズムを示そうとしない。
(Fig.26) スピン・軌道相互作用は 幻想である。
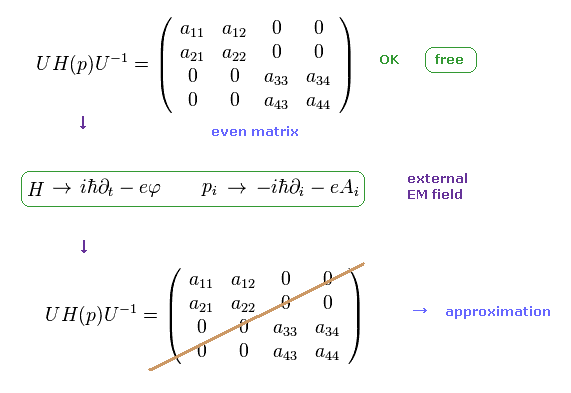
このページに示したように ディラック行列 (= フェルミ粒子 ) は 4 × 1 行列である。
そして 上下部の 2つのスピノルは 混合しており、これは 通常の 非相対論的な場の量子論とは 異なる。
そのため Fig.26 上に示した 対角化行列 U を用いて ディラック行列から 偶行列を得る必要がある。
しかし ハミルトニアン H が 外磁場 (= A, φ ) を含んでいるとき、何らかの近似に頼らない限り 偶行列を得ることはできない。
(Fig.27) 近似 → スピン・軌道相互作用項は 本当に表れた?

何らかの近似 (= パウリ近似 ) に頼ることによって、スピン・軌道相互作用項が 得られると 彼らは主張している。
重要な点は 相対論的な場の量子論に基づく このスピン・軌道相互作用というのは 実際の実験値に比して 非常に弱いのである。
(Fig.28) スピン・軌道相互作用の比較。
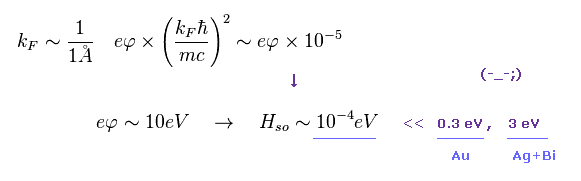
Fig.28 では、 kF は近似的な波数で、 電気ポテンシャル (= eφ ) を約 10 eV (= 外殻電子 ) とした。
これらの値を用いると ディラック方程式による スピン・軌道相互作用は 約 10-4 eV と 非常に弱くなる。
この値は Au や Ag+Bi などの金属表面に現れる スピン・軌道相互作用 ( それぞれ 0.3 eV と 3 eV ) などの実験値と比して 桁違いに弱い。
そのため 彼らは 人為的に スピン・軌道相互作用係数を 様々な金属において もっと大きな値に変えてしまった。
( つまり これらの係数は 自由に設定可能なパラメーターと言える。)
結論からして このように スピン・軌道相互作用とは "理論的"にも "実験的"にも まったく裏付けのない存在なのである。
(Fig.29) パウリの排他原理の原因は "力" ? → "つまらんことは質問するな。"
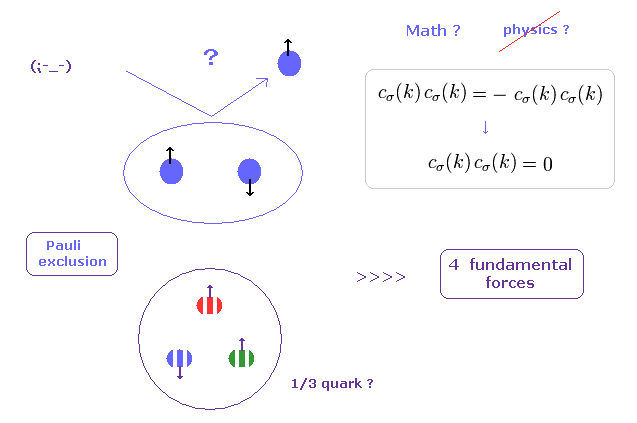
何かしらの物性物理学の教科書を見れば分かるが、一見して それらの本の中には 非現実的な "スピン" の語句で溢れかえっているのが分かる。
その主要な要因は "パウリの排他原理" にあると言っていい。つまり 2つの同じ状態のフェルミ粒子は 同じ場所に入れない。
( しかし この”同じ場所”という定義が 非常に曖昧である。物理的に 境界線を はっきり定めることもできないのに。)
例えば、1s エネルギー準位では スピン "up" と "down" の電子のみしか 入れない。
彼らは クォークにおいてさえ パウリの排他原理を強引に満たすため 非常に人為的な "カラー" (= 赤、青、緑 ) なる概念を導入した。
つまり この謎めいたパウリの排他原理を引き起こす"力"というのは 他の4つの基本的な力よりも はるかに強力なものと言える。
問題は 物理学者達は 決して このパウリの排他原理の実態を 21 世紀になった今でさえ 調べようとしないことである。
莫大な経費を 役に立たない 非常に高価な加速器なんかに浪費する前に このパウリの排他原理の正体を 真先に調べるのが 道理であろう。
(Fig.30) スピン・スピン相互作用は 幻想である。

Fig.5 と Fig.6 に示したように、スピン・スピンの磁気相互作用というのは 強磁性を生じさせるには 余りにも弱すぎるのである。
そのため 彼らは 交換相互作用 J の強さは 何らかの 曖昧な 量子力学的効果による と主張し始めた。
つまり "量子力学的な効果" というワードは よく分からない現象を説明するのに 非常に便利な 言い回し なのである。
彼らは 非現実的な "準粒子"も含めて これらの曖昧な概念を すみやかに 明らかにすべきである。
(Fig.31) "同調しあった" ドブロイ波 が 強磁性の本質である。
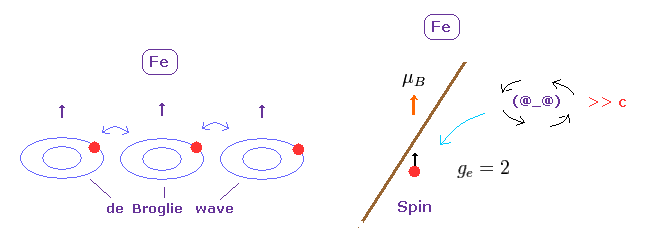
もし 奇妙な "スピン" 磁気モーメントが 強力な 強磁性を生じるのに 弱すぎるとしたら、この現象を説明できるのは たった一つしか残っていない。
お気づきのとおり、各電子の運動によって生じる ドブロイ波が 互いに 同調しあっているとしたら 強磁性の安定性を 自然に説明することができる。
上で説明したとおり、現在の物性物理学は 暗黙のうちに このドブロイ波に "位相" やら 波数 などの形で 頼っているのである。
( しかし 彼らは 決して この実在的な波を認めようとせず、 ただ "黙って計算だけしてろ" の姿勢を繰り返すだけである。)
(Fig.32) 電子スピンは 幻想である。
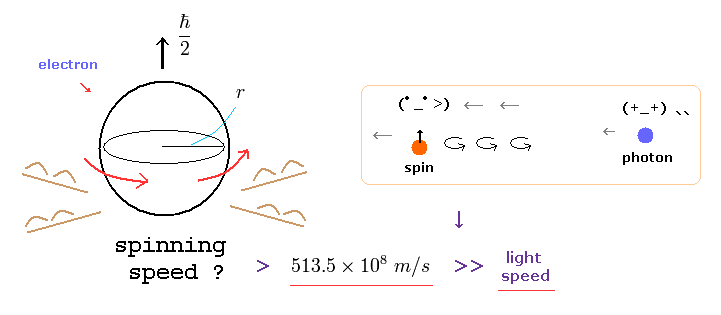
なぜなら このページに示したように、彼らが スピンとは いったい何なのか 問おうとした瞬間に スピンが 単なる古典的な軌道運動によるものということに 気づいてしまうからである。
残念ながら 現在の物理学者達が このスピンを修正するには ちょっと遅すぎると言わざるを得ない。
なぜなら ”スピン” を否定することは 量子力学 から 場の量子論まで すべてを否定することに 等しいからである。
結果的に 現在の物理では 量子力学的世界を説明するのに 想像上の 余剰次元や 別世界の周囲をうろうろするしか他に術がない状態なのである。
(Fig.33) s-d 相互作用は 弱すぎる。
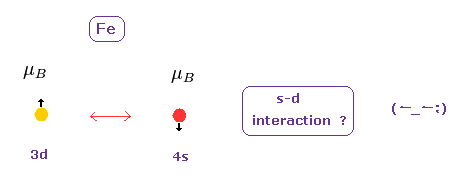
3d と 4s 軌道の電子のスピンが 互いに相互作用しあって 物質内で 様々なマクロな効果を生じさせると言われている。
しかし Fig.30 のように この s-d スピン相互作用は スピン磁気モーメントが この効果を起こしていると考えるには あまりのも弱すぎるのである。
(Fig.34) s-d 相互作用は 弱すぎる。
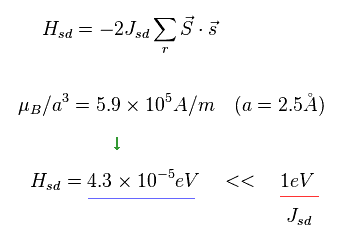
格子の原子間距離を 2.5 Å とする。
この間隔において、"スピン"磁気モーメントを用いて 何らかのエネルギー値を得ようとすると このエネルギーは 実際の相互作用値 (= 1 eV ) と比べて 弱くなりすぎるのである。
そのため また 彼らは これは 何らかの他の"量子力学的"な現象によると主張し始めた。
しかし 奇妙な”スピン”には元から実態というものがないのである。
この事実は 強力な s-d 相互作用が スピンではなく、 明らかに 他の ドブロイ波などの要因によって生じていることを示している。
(Fig.35) AMR は 異なったドブロイ波の方向によって生じる。
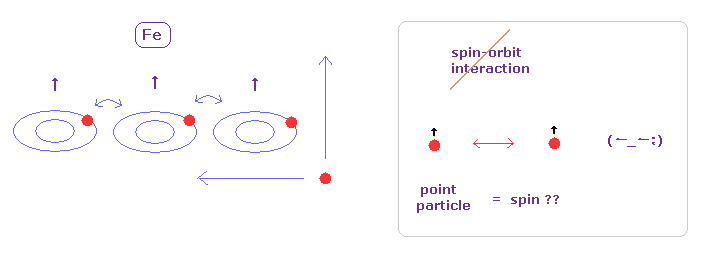
磁性体において 電流と磁化の方向に応じて 電気抵抗が変化することが知られている。
この現象を 異方磁気抵抗 (= AMR ) という。
彼らは 強磁性は Fe などの金属の "3d" 電子のスピンによって生じるとしている。
つまり 彼らの理論によれば AMR は スピンと軌道 (= 電流 ) の相互作用によって生じることになる。
Fig.6 と Fig.28 に示したように、"スピン" とは異なる別のものが これらの強磁性や スピン・軌道相互作用に主要な役割を果たしていることは 明白な事実である。
すると この AMR というのは 点状粒子のスピンなどではなく、
ドブロイ波の方向の違いによって生じると考えるのが自然である。
(Fig.36) GMR は スピン・軌道相互作用 ? もしくは 電子散乱?
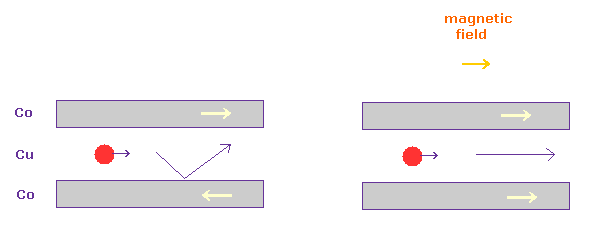
Fig.36 では、 非常に薄い (= 10 Å) 非磁性層 (= Cu ) が 磁性体 (= Co, Fe ) によって挟まれている。
このケースでは 上下部の Co の層の磁荷の方向が 互いに異なるとき (= Fig.36 左 )、Cu 層の 電気抵抗は 著しく強くなる。
この現象を 巨大磁気抵抗 ( GMR ) という。
この GMR は 何らかの電子散乱や スピン・軌道相互作用によって生じるとされているが この本当のメカニズムは 謎のままである。
強磁性自体が スピンとは異なる別のものによって生じることを考慮すれば、この GMR も ドブロイ波の方向の違いによって生じると考えるのが自然である。
(Fig.37) ホール効果。
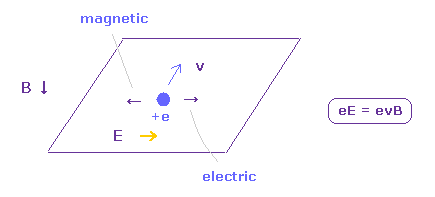
ホール効果では 荷電粒子は 磁場 (= B ) と 電場 (= E ) の両方に 垂直な方向に動く。
この現象は 通常の 古典的なローレンツ力による。( 教科書をみてもらえば分かる。)
Fig.37 では、 電気力 ( eE ) は 磁気ローレンツ力 (= evB ) にちょうど等しい。
この電流 (= "v" ) を "ホール電流" という。
(Fig.38) 異常ホール効果。
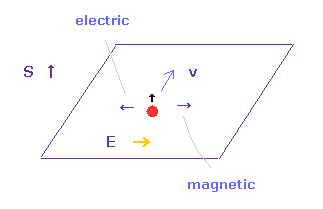
異常ホール効果では 内因性の強磁性による磁場が ホール効果の外磁場のような役割を果たしている。
そのため 彼らは この効果は スピン・軌道相互作用によって生じるとしている。
( なぜなら 彼らは 強磁性自体が 非現実的な "スピン" によるとしているからである。)
非磁性体においては、この電流は それらの磁気モーメントの方向に応じて 2つの逆の方向に分離する。 ( = スピンホール効果 )。
Fig.37 と Eq.38 に示したように、これらの効果は 軌道磁気モーメント ( スピンでなく ) と 電流の相互作用によって生じると言える。
このページを見てお分かりになった通り、これらの実験結果は まったくと言っていいほど 非現実的な "スピン" の実在の証明にはなっていないのである。
つまり "スピン" というのは 単なる "想像上" の概念と言える。
(Ap.1)
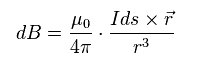
ビオ・サバールの法則によれば、磁場 (= B ) は Ap.1 に示したようになる。
"I" は 電流、 "ds" は 電流断片、 "r" は この断片と ある地点との距離である。
(Ap.2)
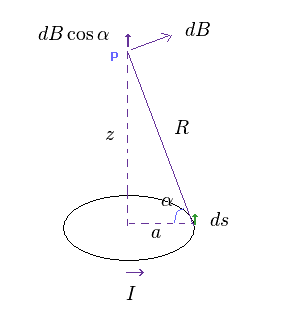
ここでは Ap.2 のような 円形の電流について考える。
"p" の地点の 磁場 B は 電流断片 "Ids" の 円周一周の合計である。
Ap.2 に示すように、 B の コサイン成分のみが 円電流の磁場を合計した後に残る。
(Ap.3)
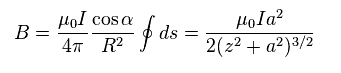
ここでは
(Ap.4)
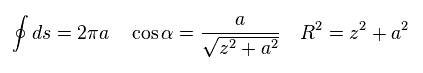
単一電子が 非常に小さいことを考慮すると、Ap.2 で 半径 "a" は "z" に比して非常に小さい。
つまり 近似的に Ap.3 は、
(Ap.5)
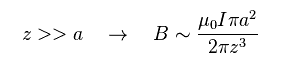
もちろん、Ap.3 の分母で "a" を残しても、この磁場は さらに小さくなる。
このページに示したように、 ボーア磁子 (= μB ) は IS (= 電流 × 面積 ) で与えられる。
(Ap.6)
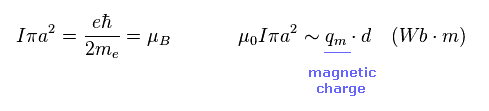
Ap.6 に示したように、磁気モーメントは 磁荷 (= q ) × 距離 (= d ) に等しい。
この "d" は 単一の磁気モーメント内での "仮想の" ± 磁荷 "q" 間の短い距離を表している。
( もちろん、これは単なる仮定で 磁荷自身 実在しない。)
(Ap.7)
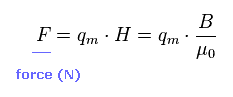
力 (N) と 磁場の関係式は Ap.7 で与えられる。
Ap.7 では、 "B" は 磁束密度 ( Wb/m2 )、 μ0 は 透磁率である。
(Ap.8)
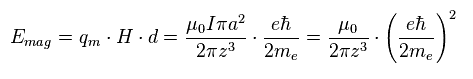
2つの スピン磁気モーメント間の距離が "z" のとき、磁気エネルギーは Ap.8 のようになる。
なぜなら エネルギーは 1つのスピン内の 磁気力 × 距離 "d" に等しいからである。
( つまり 磁場 B の環境で ± の磁荷 q を 距離 "d" 引き離すのに必要なエネルギーである。)
この磁気力は Ap.7 で与えられ、"B" は Ap.5 で与えられる。
( もちろん、スピン磁気モーメントは Ap.6 の ボーア磁子である。 )
(Ap.9)
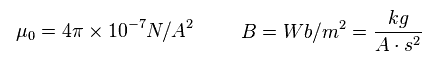
透磁率と磁束密度の SI 単位は Ap.9 のようになる。
(Ap.10)
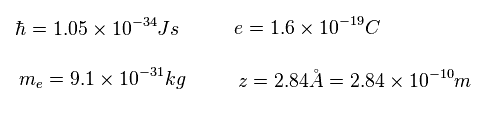
Ap.9 と Ap.10 を用いて、Ap.8 を計算する。
結果は、
(Ap.11)
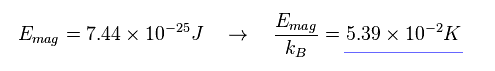
このエネルギーを ボルツマン定数 kB で割ると、この スピン・スピン相互作用というのが 非常に小さい ( 0.0539 ケルビン ) ことが分かる。
つまり もし 強磁性が スピン・スピン相互作用によって生じるとすると、この磁石は 室温で 簡単に 壊れてしまうことになる。
この結果は "強磁性" というのが 明らかに "スピン" とは 異なる別のものによって 起きていることを示している。

2013/9/10 updated This site is link free.