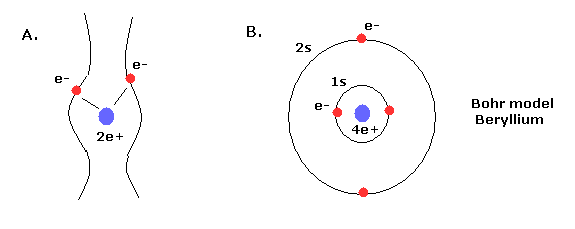
Top page (correct Bohr model including the two-electron atoms)
Schrodinger equation is only one part of Bohr-Sommerfeld model
Rigorous proof that Schrodinger equation belongs to Bohr-Sommerfeld model
Since Bohr's theory in 1913, various physicists such as Sommerfeld, Kramers, Pauli, Heisenberg, Lande, and Langmuir tried to get correct Bohr model helium structure.
The ordinary physics textbooks often say Bohr's atom radiates and loses energy due to the accelerating charge.
But this explanation is incorrect.
Because the vacuum electric (magnetic) energies around a single charged particle can NOT be expressed using classical electromagnetism theory.
The vacuum electric energy is equal to the sum of the potential energies among infinitesimal charges included in the single charged particle according to the classical theory.
But a single electron is NOT made from smaller infinitesimal charges, and NOT broken. (See this page)
So the Poynting vector and the vacuum electric energy themselves do NOT apply to the single electron's case.
Actually many great physicists aimed at getting Bohr's helium atoms in 1920s.
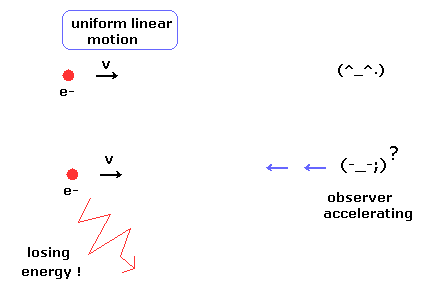
(Fig.1) Observer's supernatural power ?

According to the relativity, all phenomena must look the same irrespective of the observer's movement.
( But this very strict limitation has removed reality in the relativistic quantum field theory and string theory )
In the upper panel of Fig.1, a single charged particle is moving linearly at the constant velocity (= uniform linear motion ).
And the observer is at rest, so the moving charged particle does NOT lose energy according to the ordinary textbooks.
But in the lower panel of Fig.1, the observer starts to accelerate.
According to the relativity, from the observer's viewpoint, the charged particle is accelerating instead of the observer.
So the charged particle is losing energy (= kinetic energy ), though its motion does NOT change from the upper panel of Fig.1 !
This means observer's supernatural power ? It is very strange.
(Fig.2) Old Bohr's helium atom
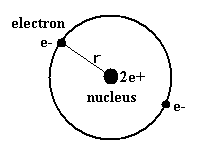
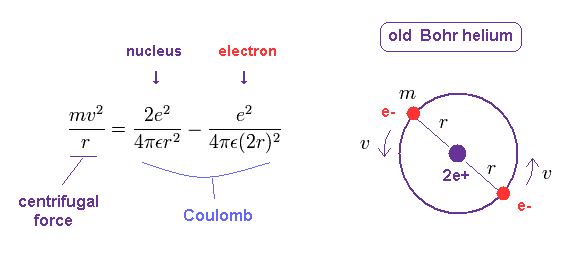
In the helium atom which Bohr first thought up, two electrons are moving on the same circular orbit at the opposite sides of the nucleus (Fig.2).
But as shown in this page, the ground state energy of this old Bohr's helium is -83.33 eV, which is different from the experimental value -79.005 eV ( by about 5.5 % ).
And this simple helium model has magnetic moment , and always gives an integer times Bohr magneton ( too simple ! ).
Of course, this old model contradicts the Davisson-Germer experiment, because their opposite phases cancel each other out, which expels one of the electrons from the orbit.
( See also Pauli exclusion principle by Bohr model is more useful. )
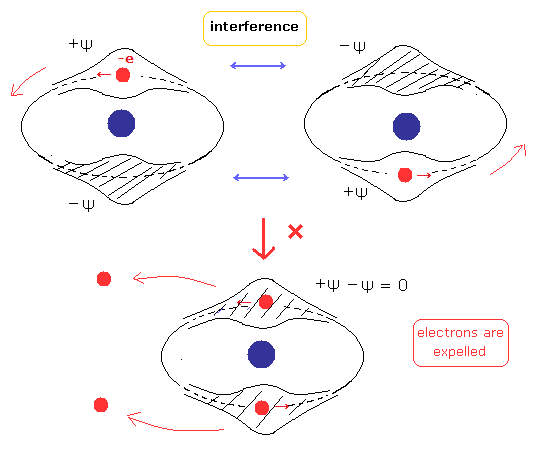
(Fig.3) Two de Broglie waves of electrons interfere with each other.
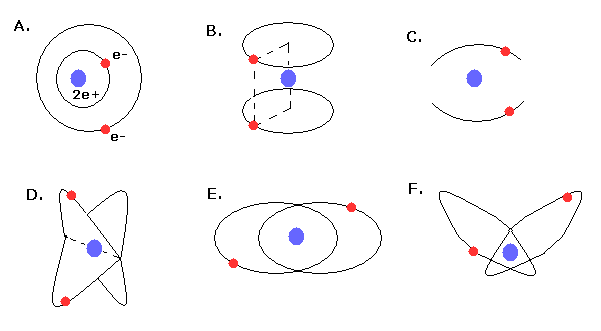
In 1910s - 1920s, Lande (= outer and inner orbits, Fig.4A), Langumuir (= two parallel orbits, Fig.4B, two linear oscillating orbits, Fig.4C), Kramers (= 120 degree angle crossed orbits, Fig.4D ), and Heisenberg (= coplanar and inclined orbits, Fig.4E,F ) were trying to get better Bohr's helium atom.
But No old helium models could explain the correct ground state energy, stability, and closed shell property of helium atom.
(Fig.4) Various old Bohr's helium atom.
Even after 1980s, various Bohr's helium models were thought up ( See also arxiv 0705.4321v2 ).
For example, two electrons are moving on the same orbit, but they are permitted to move relative to each other around the orbit.
( Fig.5A, J Phys.B, At.Mol.Phys. 16, 2647-2657, 1983, Bohr orbit theory revisited. ).
And Fig.5B shows coplanar Bohr's beryllium atom ( http://www.users.csbsju.edu/~frioux/stability/BohrAtoms.pdf ).
But they could not replace the quantum mechanical variational methods in the calculating results.
Semiclassical "WKB" method is one of the quantum mechanical methods, which is different from original Bohr model.
See also ( Theoretical and Mathematical Physics, 151, 659-680, 2007, semiclassical quantization of Bohr orbits in the helium atom ).
This result differs by 6% from the experimental values of ground state energy.
(Fig.5) Some examples of Bohr's helium atoms
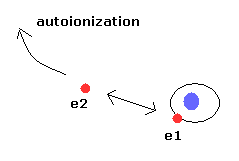
Using computers, in the three-body problems including repulsive Coulomb force between electrons, the electrons' orbits show a chaotic behavior by any slight change of initial conditions, and lead to an escape of one electron (= autoionization ).
(See Phys. Rev. Lett. vol.70, 13, 1928, 1993, Helium atom as a classical Three-Body Problems )
This means almost all cases show unstable autoionization (= one of the two electrons goes to infinity ) in the classical helium atoms.
(Fig.6) Autoionization in the classical helium atoms
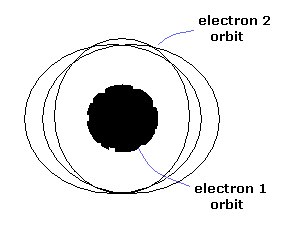
Only three patterns (tori) are stable.
One of them is a model of the inner and outer double rings (Fig.7).
When the two electron's orbits are apart from each other, they are like two elliptical orbits.
As the two electrons get closer, the torus orbit is deformed strongly.
(Fig.7) Classical helium atoms
In the second pattern, one electron revolves twice in the inner side, while the other revolves once at the outer circle, and then exchange their positions.
And the third pattern shows the inner and outer electrons are oscillating asymmetrically.
Of course, if we apply some external forces to these classical helium models, they become unstable and easily cause autoionization.
And it is impossible that we consider an integer times de Broglie wavelength in these complicated asymmetric classical helium.
(Fig.8) Quantum mechanical helium is also unstable.
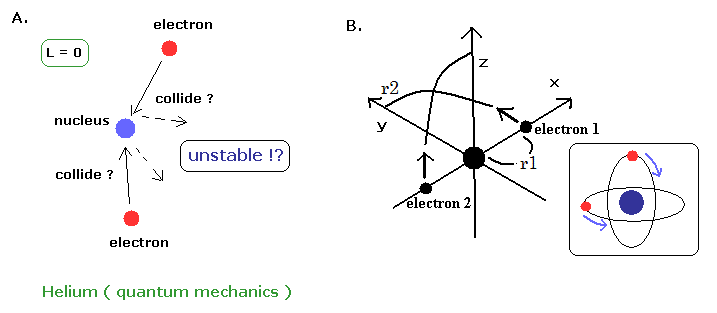
If the classical helium such as Fig.7 is unstable, the quantum mechanical helium (Fig.8A) is also unstable.
Because the angular momentum of both two electrons are zero ( L=0 ), which means the two electrons always collide with the nucleus and rebound from it !.
( The wave phases of this quantum mechanical helium become chaotic, I think. )
On the other hand, in the new Bohr model helium, their wave phases are stable, NOT cancel each other, because their orbits are just perpendicular to each other. (= NOT contradict Davisson-Germer experiment. )
And in this new model, the orbit is just one de Broglie wavelength like the hydrogen atom.
( Computed ground state energy -79.0035 eV is more accurate than the latest quantum mechanical methods. )
As shown in this page, it is very important that the two electrons have definite and stable orbits due to de Broglie wave interference.
If the two electron's orbits easily change under some external Coulomb forces, their wave phases become chaotic and cancel each other.
( Because two electrons are at almost opposite positions. )
But as you know, the helium atom is very stable and inactive in all atoms.
So Fig.8B helium model is very reasonable.
(Fig.9) New Bohr's helium (= A.) is not polarized.
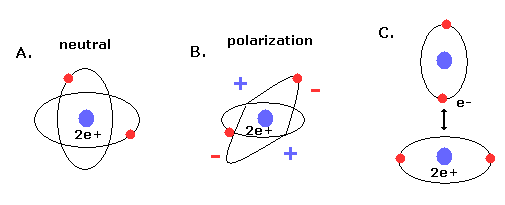
Furthermore, if the two electrons are just symmetric and perpendicular to each other, there are no imbalance of the minus charged electrons around the nuclues (= neutral, Fig.9A ).
If the two orbits are asymmetric, the space around the nucleus is polarized (= plus or minus charges in Fig.9B).
The polarized atoms tend to interact with each other and form weak binding (see also Fig.9C).
So in this case, the helium easily becomes "liquid", which contradicts the fact.
(Fig.10) Old Bohr's helium. Two de Broglie waves cancel each other.
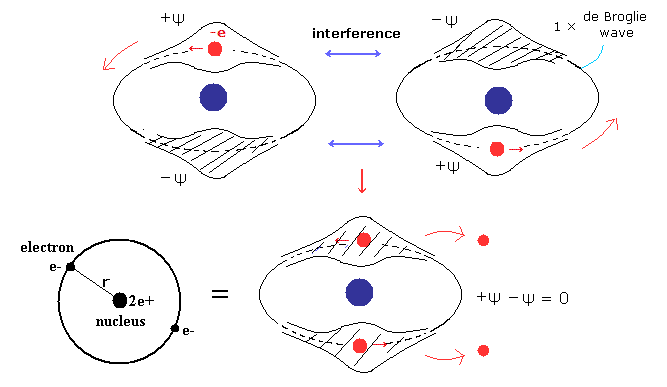
In old Bohr's helium (Fig.10), two electrons are moving on the opposite sides of the nucleus in the same circular orbit (= one de Broglie wavelength ).
Considering Davisson-Germer experiment, two electrons of old Bohr's helium are clearly unstable due to de Broglie wave destructive interference. ( Opposite wave phases, ±ψ exist on the other sides in 1 × wavelength orbit.)
Actually, old Bohr's helium of Fig.41 gives wrong ground state energy of helium.
In circular orbit of helium, equating the centrifugal force to the Coulomb force, we have
(Fig.11) Old Bohr helium.
where r is the circular orbital radius (meter), e is the electron charge
The circular orbital length is supposed to be an integer (n) times de Broglie's wavelength of the electron, we have
(Fig.12) Circular orbit = 1 × de Broglie wavelength.
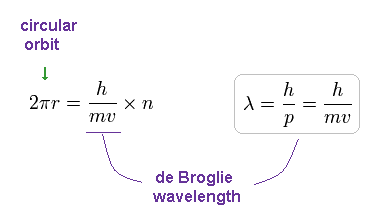
where h/mv means the de Broglie's wavelength.
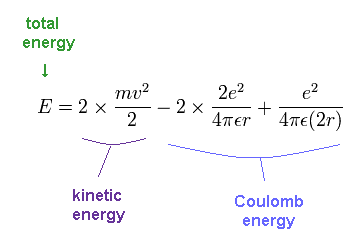
The total energy E of the helium is the sum of the kinetic and the Coulomb potential energy of the two electrons, so
(Fig.13) Energy of old Bohr's helium.
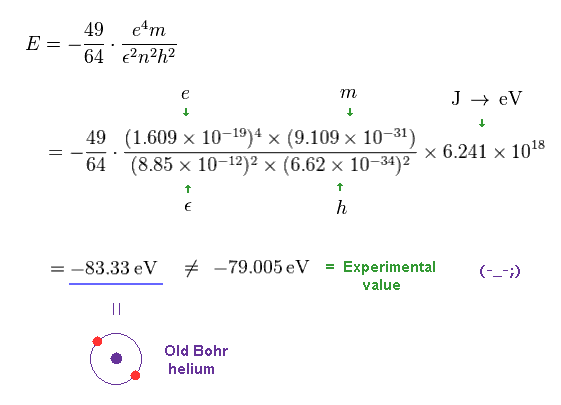
Solving the above three equations ( Fig.11-13 ), the ground state energy ( n=1 ) becomes - 83.33 eV.
This value is lower than the experimental value -79.005 eV.
(Fig.14) Old Bohr's helium does NOT agree with experiments.
Furthermore when some atoms such as oxygen come close to old Bohr's helium, its wave phases easily become chaotic due to the external force of other atoms, which is inconsistent with strong stability and closed shell property of helium atoms.
(Fig.15) Old Bohr's helium can NOT keep 1 × de Broglie wavelength
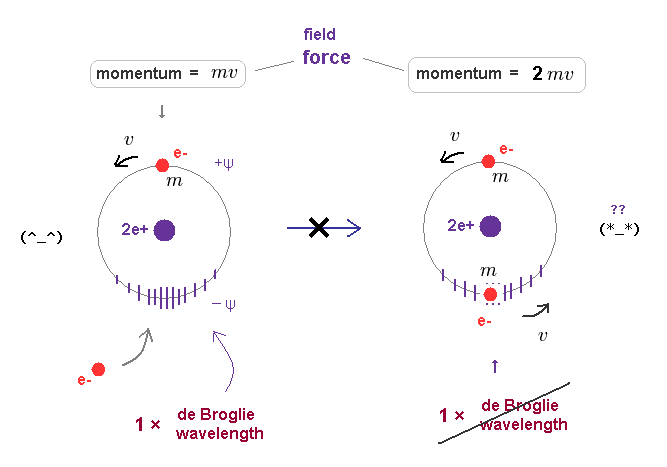
In Fig.15 left, only one electron is moving around helium nucleus.
This orbital length is just 1 × de Broglie wavelength, which means "stable".
Of course, the field in this orbit is affected by the electron's momentum (= mv = pressure ) and contracts depending on its strength.
In old Bohr's helium model, two electrons are moving in the same one orbit on opposite sides of nucleus.
When another moving electron enters the same orbit, the force (= pressure ) acting on their surrounding field becomes twice ( mv → 2mv ).
As a result, the original 1 × de Broglie wavelength cannot be kept as it is in Fig.46 right.
See mechanisms of de Broglie wave and all atomic structures.

2012/8/28 updated. Feel free to link to this site.