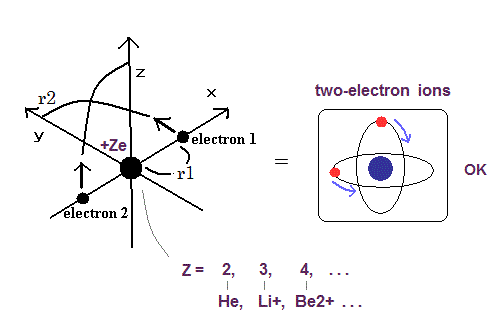
Top page (correct Bohr model including the two-electron atoms)
Electron spin is an illusion !
There are no stable chemical compounds of helium atom.
Quantum mechanics says that the closed 1S shell with spin up and down electrons causes this stable and solid property.
But it doesn't say anything more about this reason.
For example, also in the hydrogen molecule (H2), the spin up and down electrons form one stable bond structure.
But H2 molecules react with the oxygen easily and explosively.
The magnetic moment of the electron spin is too small to prevent the helium atoms from forming compounds.
So why can't the helium atom form compounds with other elements (or helium itself) ?
The helium's boiling and melting points are the lowest among the elements.
Of course, the four fundamental forces of nature can not explain this reason.
In this page, we explain this reason properly using our new Bohr's helium model.
The ground state of the hydrogen atom has an orbit of just one de Broglie's wavelength.
(This corresponds to Bohr model and Schrodinger's hydrogen, as shown on this page.)
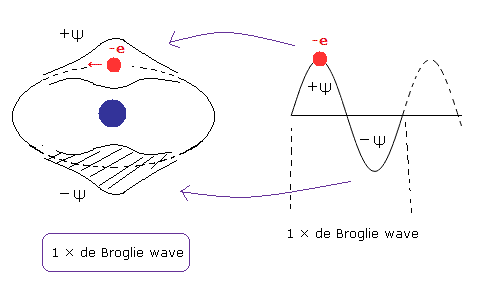
(Fig.1) One de Broglie wavelength orbit contains only one electron.

If this ground state orbit can contain more than one electrons, the orbital length of one electron can be shorter than the original one, which makes the ground state energy lower.
And the two slit or Davission-Germer interference experiments showed that the electrons are always pushed to some limited spaces (phase) in one de Broglie wavelength region.
Here we call this limited spaces (phase) +Ψ as shown in Fig.1.
(Of course, +Ψ can interfere with -Ψ and +Ψ itself.)
(Fig.2) Old Bohr's helium atom.
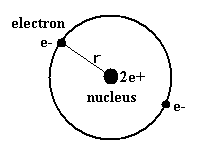
As shown on top page, old Bohr's helium model of Fig.2 gives incorrect energy value. (= -83.33 eV.)
(Experimental value of the neutral helium atom is -79.005147 eV.)
In Fig.2 orbit, the two electrons are packed in one orbit of one de Broglie's wavelength.
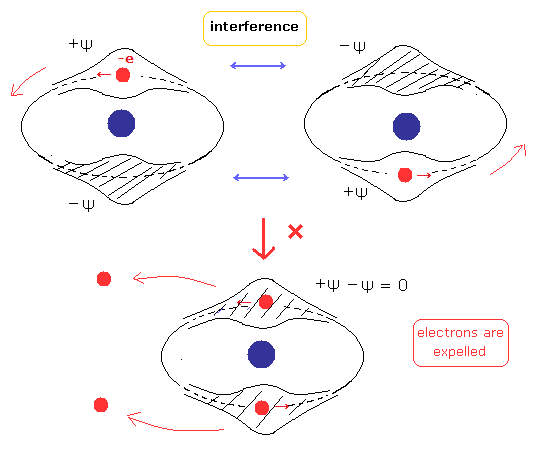
So considering Fig.1, the phaes of +Ψ and -Ψ interefere with and cancel each other.
As a result, there are no spaces for electrons to enter in Fig.2 orbit. (See also Fig.3.)
(Fig.3) There are no electron spaces in old Bohr's helium atom.
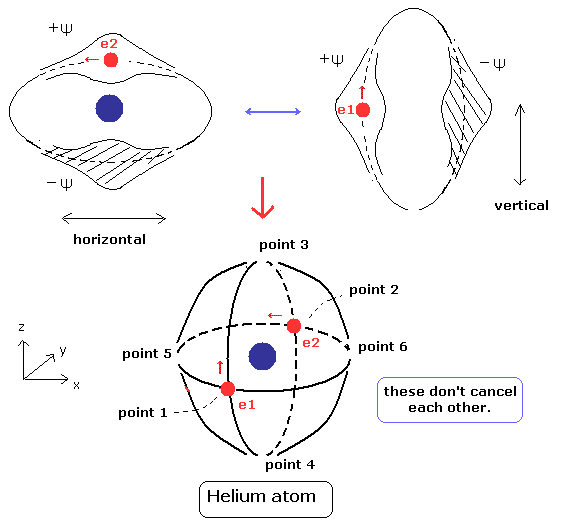
But if two orbits of helium are perpendicular to each other like Fig.4, the two de Broglie waves don't interfere with each other.
As a result, the two de Broglie's waves, which are independent from each other can oscillate stably and periodically.
(Fig.4) Stable and independent two de Broglie waves. (= perpendicular to each other.)
As shown on top page, Fig.4 helium model gives the most accurate result. (= -79.0035 eV, relativistic correction is -0.001647 eV).
(Of course, this result is more accurate than the latest variational method based on Schrodinger equation.)
And Fig.4 model can explain the closed shell property and Pauli exclusion principle of the helium atom correctly, which are written in later section in detail.
There are two intersection points in Fig.4 helium. (points 1 and 2.)
(Fig.5) State of intersection point 1 in Fig.4.
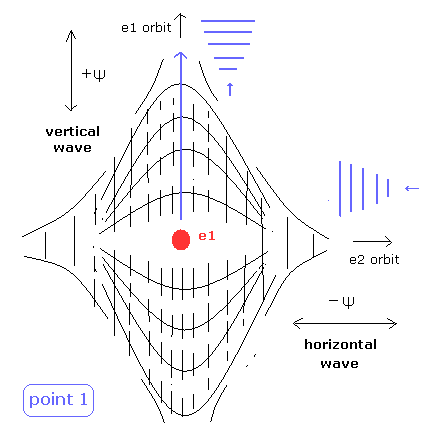
In Fig.5, the vertical de Broglie wave is electron 1, and the horizontal wave is electron2.
The phases of +Ψ and -Ψ are perpendicular to each other.
So they don't cancel each other, which gives electron 1 space, as shown in Fig.5.
When the horizontal component of electron 1 velocity is not completely zero in Fig.5, this means that there is a +Ψ space of the electron 1 in the horizontal direction.
But the phase in the horizontal direction of point 1 is opposite (-Ψ), so there is no space of it.
(+Ψ × 2 is needed. +Ψ × 2 - Ψ = +Ψ. But of course, it doesn't exist.)
As a result, the two de Broglie waves need to be just perpendicular to each other.
(Fig.6) State of intersection point 2 in Fig.4.
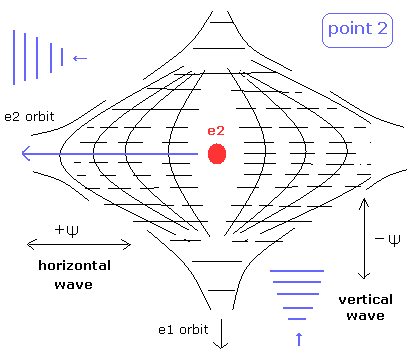
Also in the point 2 of Fig.4, the two de Broglie waves are perpendicular to each other.
So there is electron 2 space in the intersection point.
It is thought that the states at the intersection points are changing periodically among Fig.5, intermediate state, and Fig.6.
(Fig.7) Two de Broglie waves "always" need to be perpendicular to each other.
For example, according to Davisson-Germer interference experiment, the width of de Broglie wave needs to be more than at least 0.091 nm (= 9100 MM).
Because it uses the nickel, which spacing is d = 0.091 nm.
As shown on top page, the radius of our new Bohr's helium is about 3100 MM.
This means that not only intersection points but also all other spaces of a helum atom need to have two de Broglie waves, which are perpendicular to each other.
The helium is a small atom. So if the width of one de Broglie wave is smaller than helium radius, we can not observe the electron's interference in the actual experiments with the crystals of various elements.
(Fig.8) Electron 2 wave cancels itself at point 3 of Fig.4.
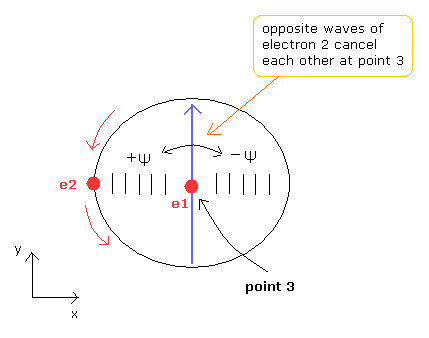
As Fig.4 helium model has symmetrical structure, the opposite phases of electron 2 de Broglie waves (see Fig.8) cancel each other at point 3 of Fig.4.
As a result, the electron 1 de Broglie's wave keeps stable and independent also at point 3.
(Fig.9) Two orbital planes can cross at the angles other than 90 degrees ?
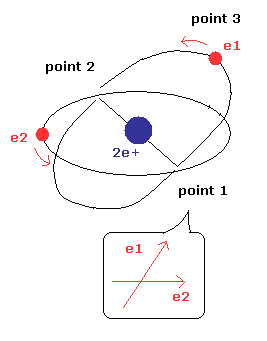
In Fig.9, the two orbital planes cross at the angles other than 90 degrees.
But as I said above, this case is impossible, because there are no spaces in which two electrons are moving in the same directions in the helium atom.
In Fig.9 model, both the two orbital planes includes nucleus.
Due to the repulsive force between electrons, the two orbital planes become parallel to each other.
But as I said above, this parallel state means Fig.2, and Fig.3 state, which contains two electrons in one orbit.
(Of course, this is impossible, and doesn't agree with the experimental result.)
So in Fig.9, the "wall" of electron 2 de Broglie wave needs to block the repulsive Coulomb force.
But as shown in Fig.10A, de Broglie wave's wall of Fig.9 is very unnatural.
(Fig.10) "Unnatural" de Broglie wave's wall.
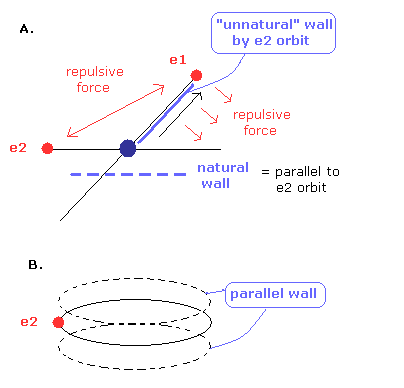
If there are any "walls" of de Broglie's waves, it is natural that the walls become parallel to the orbit like Fig.10B.
Because de Brolie's waves are generated by the electron's orbit.
So oblique walls are unnatural.
(Fig.10-2) Electron can NOT make U-turn.
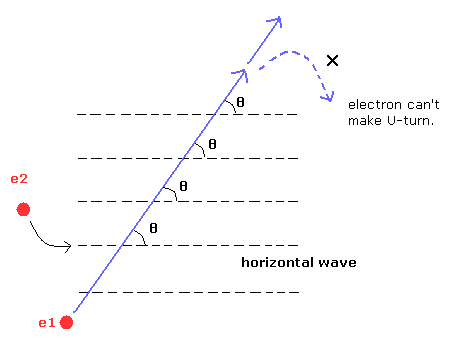
If the angle between the electron 1 (e1) and electron 2 (e2) de Broglie's waves is definite value (= θ), which is different from 90 degrees, the electron can NOT return.
In this state, the electrons would fly away somewhere.
Because this θ must be zero for the electron to make U-turn, as shown in Fig.10-2.
If this angle θ is 90 degrees, electron 1 can make U-turn through point 3, as shown in Fig.4 and Fig.8.
(Fig.11) Electron's orbits become undefined and unstable.
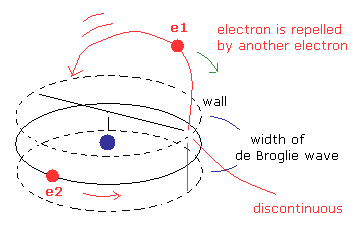
In Fig.11, we suppose the width of de Broglie wave is very narrow, though it is inconsistent with the interference experiments such as Davisson-Germer experiment.
If the wall of de Broglie waves is parallel to e2 orit like Fig.11, e1 orbit becomes very complicated and unstable.
Because, the influence by another electron is discontinuous between inside and outside the wall, as shown in Fig.11.
In conclusion, there are no other stable helium models than Fig.4
On this top page, we have succeeded in computing the most accurate ground state energy using Fig.4 helium model and sample JAVA program.
(Fig.12) Starting points - 1/4 orbit of new Bohr's helium model
(Fig.13) The two electrons have moved 1/4 orbits.
In the top page, we use the new convenient unit 1 SS = 10-25 second.
But this takes a little time (about one minute) to compute.
So here we use 1 SS = 10-23 second, which gives almost same results as top page quickly.
(Eq.1) New units of time and length.
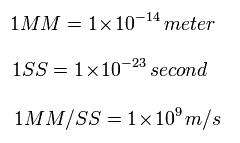
From Eq.1, the accelaration is
(Eq.2)
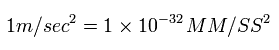
sample JAVA program 1 SS = 1 × 10-23
C language program
(In this program, we can choose the usual mass or reduced mass in the electron.)
If you copy and paste the above program source code into a text editor, you can easily compile and run this.
(This class file name is remass, so save this text editor as "remass.java", and compile it.)
In this program, we first input the number ( 1-3 ) of reduced mass conditions.
In "Normal" condition (= 1 ), we use the redeuced mass except when the center of mass is at the origin.
In "Not reduced mass" (= 2 ) condition, we always use the usual mass (NOT reduced mass).
In "All reduced mass" (= 3 ) condition, we always use the reduced mass even when the center of mass is at the origin.
Next we input the initial x-coordinate r1 (in MM) of electron 1 (see Fig.12), and the absolute value of the total energy E (in eV) of Helium.
From the inputted values, we calculate the initial velocity of the electron 1 at Fig.12.
In "Normal" and "Not reduced mass" conditions, we use the usual mass when we compute the initial velocity, because the center of mass is at the nucleus in Fig.12.
In "All reduced mass" condition, we use the reduced mass even in calculating the initial velocity ignoring this situation.
And at intervals of 1 SS, we compute the Coulomb force among the two electrons and the nucleus.
When the electron 1 is at (xx, yy, 0), the electron 2 is at (-xx, 0, yy) (in MM). (See Fig.12 and Fig.13.)
Change MM to meter as follows; x (m) = xx × 10-14. y (m) = yy × 10-14.
So the x component of the acceleration (m/sec2) of the electron 1 is,
(Eq. 3) x component of the acceleration.
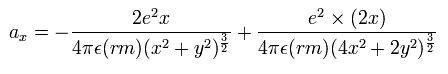
where the first term is by the Coulomb force between the nucleus and the electron 1, and the second term is by the force between the two electrons.
Considering the helium nuclear mass (= alpha particle), we use here the reduced mass ( rm =1/2 × (2me × nucleus)/(2me + nucleus) = 9.10688561 × 10-31 kg. See Eq.4.) except when the center of mass is at the origin.
(Eq. 4)
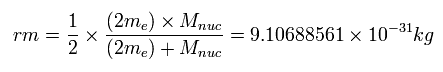
See also reduced mass of three-body helium.
In "Not reduced mass" condition (= 2 ), we always use the usual mass (NOT reduced mass) in computing the acceleration and de Broglie wave.
In the same way, the y component of the acceleration (m/sec2) is,
(Eq. 5) y component of the acceleration.
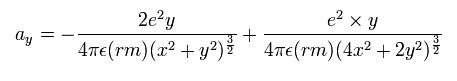
Based on that calculation value, we change the velocity vector and the position of the electrons.
We suppose electron 1 moves only on the XY-plane, so the z component of the acceleration of the electron 1 is not considered.
If we consider all components of the Coulomb force against the electrons, the electron's motion becomes as shown in Fig.2 and Fig.3.
But in Fig.2 and Fig.3, the two electrons are packed in one orbit of one de Broglie's wavelength.
So there is no space for two electrons.
We also calculate de Broglie's wavelength of the electron from the velocity (λ = h/mv) at intervals of 1 SS.
The number of that wave (λ in length) contained in that short movement section (the sum of them is WN) is,
(Eq. 6) number of de Broglie's wave contained in the short movement segment for 1SS.
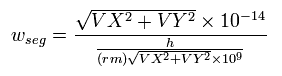
where (VX, VY) are the velocity of the electron 1 (in MM/SS), the numerator is the movement distance (in meter) for 1 SS. the denominator is de Broglie's wavelength (in meter).
Here, the estimated electron's orbit is divided into more than one million short segments for the calculation.
When the electron 1 has moved one quarter of its orbit and its x-coordinate is zero (Fig.13), this program checked the y-component of the electron 1 velocity ( last VY ).
When the last VY is zero, two electrons are periodically moving around the nucleus on the same orbitals as shown in Fig.12 and Fig.13.
So, only when -0.00001 < last VY < 0.00001 (MM/SS) is satisfied, the program displays the following values on the screen, r1, VY, preVY (VY 1 SS ago), and (mid)WN (the total number of de Broglie's waves contained in one quarter of the orbit).
Table 1 shows the "Normal condition" results in which the last VY is the closest to zero.
| E (eV) | r1 (MM) | WN | WN x 4 |
|---|---|---|---|
| -78.9900 | 3075.0 | 0.250022 | 1.000088 |
| -79.0000 | 3074.0 | 0.250006 | 1.000024 |
| -79.0037 | 3074.0 | 0.250000 | 1.000000 |
| -79.0100 | 3074.0 | 0.249990 | 0.999960 |
| -79.0300 | 3073.0 | 0.249958 | 0.999832 |
Table.1 Results of r1 and WN (number of de Broglie's waves) in which y component of electron 1 velocity in Fig.13 is zero at various energy levels of Helium.
WN × 4 is the total number of de Broglie's waves contained in one round of the orbital.
This result shows the relativistic correction to the energy = -79.005147 - (-79.0037) = -0.001447 eV.
The theoretical ground state energy value of the helium ion (He+) can be gotten from usual Bohr model or Schrodinger equation using the reduced mass.
This value is -54.41531 eV.
And the experimental value of He+ ground state energy is -54.41776 eV (Nist).
So the relativistic correction to the energy in He+ ion is -54.41776-(-54.41531) = -0.00245 eV.
The theoretical ground state energy value of the hydrogen atom (H) can be gotten from usual Bohr model or Schrodinger equation using the reduced mass, too.
This value is -13.5983 eV.
And the experimental value of H ground state energy is -13.59844 eV (Nist).
So the relativistic correction to the energy in hydrogen atom is -13.59844-(-13.5983) = -0.00014 eV.
The electron's velocity of the neutral helium atom is slower than helium ion, but faster than hydrogen atom.
So the relativistic correction in neutral helium atom should be between -0.00245 eV and -0.00014 eV.
The above calculation value of -0.001447 eV is just between them !
Table 2 shows the "Not reduced mass condition" results.
| E (eV) | r1 (MM) | WN | WN x 4 |
|---|---|---|---|
| -79.0037 | 3075.0 | 0.250071 | 1.000284 |
| -79.0300 | 3074.0 | 0.250030 | 1.000120 |
| -79.0485 | 3073.5 | 0.250000 | 1.000000 |
| -79.0600 | 3073.0 | 0.249982 | 0.999928 |
| -79.0800 | 3072.0 | 0.249950 | 0.999800 |
As shown in Table 2, if we don't use the reduced mass in the neutral helium atom, the calculation result becomes -79.0485 eV, which is different from the experimental value (-79.005147 eV).
(The error is -79.0485 - (-79.005147) = -0.04335 eV. Compare this with Table 1 result of 0.001447 eV.)
This result means we have to use the reduced mass to get the correct ground state energy in helium.
Table 3 shows the "All reduced mass condition" results.
| E (eV) | r1 (MM) | WN | WN x 4 |
|---|---|---|---|
| -79.0037 | 3075.0 | 0.250037 | 1.000148 |
| -79.0200 | 3074.5 | 0.250011 | 1.000044 |
| -79.0268 | 3074.0 | 0.250000 | 1.000000 |
| -79.0300 | 3074.0 | 0.249995 | 0.999980 |
| -79.0500 | 3073.0 | 0.249963 | 0.999852 |
As shown in Table 3, if we always use the reduced mass even when the center of mass is at the nucleus, the calculation result becomes -79.0268 eV, which is different from the experimental value (-79.005147 eV).
(The error is -79.0268 - (-79.005147) = -0.021653 eV. Compare this with Table 1 result of 0.001447 eV.)
As shown on this page, when the reduced mass is always effective (even when calculating the initial kinetic energy), the two electrons need to stick to each other like hydrogen atom.
(Fig.14) Two-body hydrogen atom.
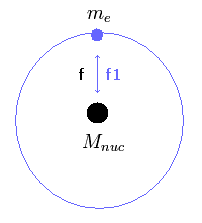
In the hydrogen-like atom, the force influencing the electron's kinetic energy is just equal to that influencing the nuclear kinetic energy.
But the two electrons of the helium can NOT stick to each other due to the repulsive force.
(Fig.15) Reduced mass of Helium atom.
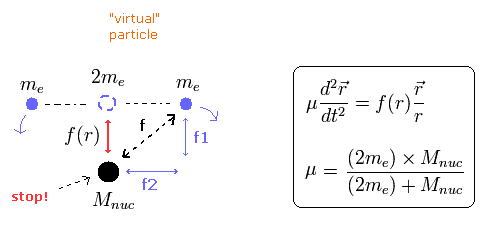
The force f2 of Fig.15 is influencing only electron's kinetic energy, but NOT nuclear kinetic energy.
The nuclear kinetic energy is influenced only by the force f1, which becomes zero when the center of mass is at the nucleus.
(Of course, the electron's kinetic energy is influenced by the forces f1 and f2.)
So when we calculate the kinetic energy (or velocity) of the electron, we can not use the reduced mass like hydrogen atom.
This fact causes the calculation error in Table 3.
(Fig.16) Nuclear movement in neutral Helium atom.
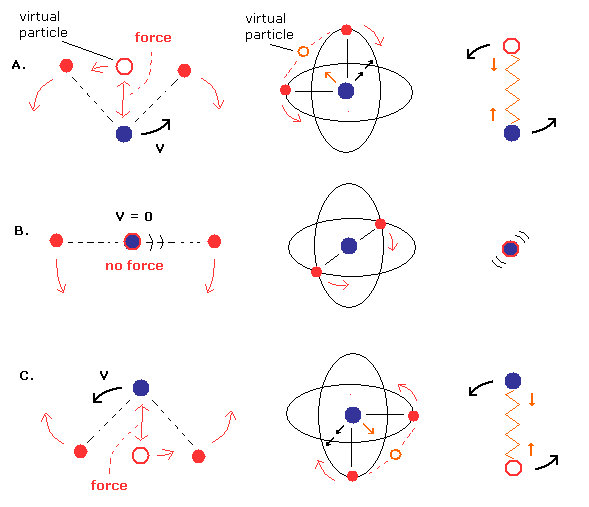
As shown in Fig.16, the nucleus is rotating by the attractive force between the "virtual" particle, which is supposed to be at the center of the two electrons.
As the center of the two electrons becomes closer to the nucleus, this attractive force becomes weaker, and the rotating speed of the nucleus becomes slower.
The middle panel (= B.) of Fig.16 shows the state in which the center of mass agrees with the nucleus.
In this state, the nuclear rotating velocity is zero. so we need to use the usual mass (Not reduced mass) when calculating the initial electron's velocity in Fig.12.
In Fig.16, the nuclei of the upper (= A.) and lower (= C.) panels have the maximum rotating velocity.
The "virtual" particle and the nucleus are coming close to (or moving away from) each other while rotating.
Fig,16 is "natural" movement pattern of the nucleus.
But we can suppose another "special" case of this movement pattern, as shown in Fig.17.
(Fig.17) Nucleus is "oscillating" instead of rotating. (= special case)
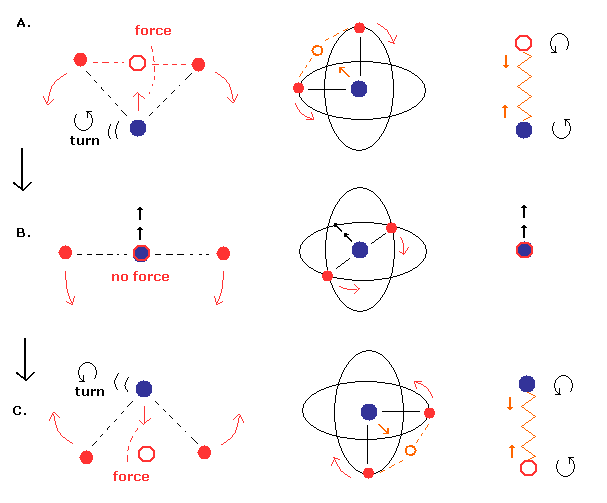
In Fig.17, the nucleus is oscillating like a spring. (= straight-line motion )
Different from Fig.16, the nuclear velocity (not rotating) becomes maximum, when the center of mass is at the nucleus (middle panel B.).
And in the upper (= A. ) and lower (= C.) panel of Fig.17, the nucleus turns back, so its velocity becomes zero at these points.
By the way, does the energy result of Fig.17 pattern become the same as Fig.16 (= Table 1) ?
Next we compute the ground state energy of the neutral helium when its movement pattern is Fig.17.
sample JAVA program (= the nucleus is oscillating like Fig.17)
C language program
If you copy and paste the above program source code into a text editor, you can easily compile and run this.
In this program, we first input the initial y-coordinate r2 (in MM) of electron 1 (see Fig.18), and the absolute value of the total energy E (in eV) of Helium.
From the inputted values, this program outputs the x component of electron 1 velocity in Fig.19, and WN (the number of de Broglie's waves contained in one quarter of the orbital). Here 1 SS = 1 × 10-23 second.
(Fig.18) Starting positions of Fig.17 model.
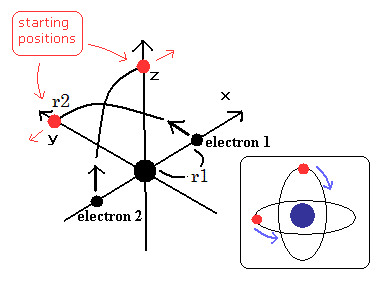
(Fig.19) Electrons have moved one quarter of their orbits.

We choose the positions of Fig.18 as the starting points.
Because in Fig,17 moving pattern, the helium nucleus stops when the electrons are at the positions of Fig.17 A and C.
So we use the usual electron mass (NOT reduced mass), when we calculate the initial velocity of Fig.18.
(After starting, we use the reduced mass.)
Table 4 shows the result of "nuclear oscillating model" of Fig.17. ( last VX = 0 )
| E (eV) | r2 (MM) | WN | WN x 4 |
|---|---|---|---|
| -79.0000 | 3137.0 | 0.250011 | 1.000044 |
| -79.0037 | 3137.5 | 0.250005 | 1.000020 |
| -79.0069 | 3136.5 | 0.250000 | 1.000000 |
| -79.0100 | 3136.0 | 0.249996 | 0.999984 |
| -79.0300 | 3135.5 | 0.249964 | 0.999856 |
As shown in Table 4, r2 is a little longer than r1 due to the repulsive force between electrons.
And the result of Table 4 is -79.0069 eV, which is a little different from -79.0037 eV of Table 1.
Of course, this result is more accurate than Table 2 and Table 3.
But only the relativistic correction can not be explained in Fig.17 (= Table 4) model.
The nuclear linear motion in Fig.17 model is very "special" case, which doesn't occur naturally.
For example, the planets which attract each other usually rotate (not oscillate).
If we always use the usual electron mass in Fig.17 even after starting, the calculation result becomes -79.0485 eV, which is completely the same as Table 2 (NOT reduced mass condition).
And if we always use the reduced mass in Fig.17 even at starting positions, the calculation result becomes -79.0268 eV, which is completely the same as Table 3 (All reduced mass condition).
This results shows that we can not discriminate between nuclear linear motion and rotating motion when we ignore the relative mass condition.
And the calculating results show that the nuclear rotating model of Fig.16 (= Table 1) is correct.
As shown in Fig.4 and Fig.7, for the two electrons to move stably aroud the helium nucleus, the two orbits always cross at 90o angle.
If this symmetric structure is broken a little, this means there are no space in which the two electrons are moving.
The radius of 2S orbit (= 2 de Broglie wavelength) is 4 times longer than 1S orbit according to Bohr model.
So if only one of the two electrons exists in 1S orbit, the ground state energy becomes much higher than the original value.
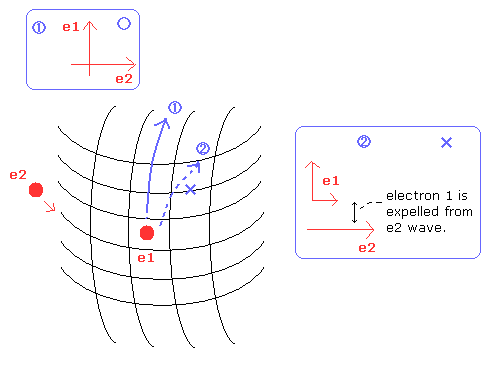
(Fig.20) Forming compounds means destruction of "symmetric" structure.
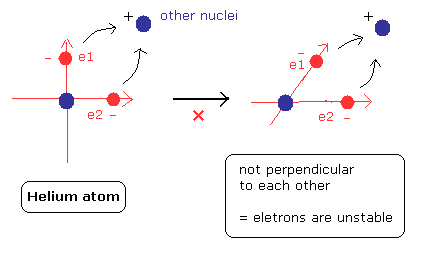
When a atom forms compounds with other elements, the electrons are a little attracted to the other positive nucleus.
This change of the structure causes the binding energy.
But as shown in Fig.20, if the neutral helium form compounds with other elements, the right angle relation between the two orbits is broken.
This means one of the two electrons are expelled from 1S orbit into 2S orbit.
As a result, the ground state energy becomes much higher (= unstable) than the original value.
So instead of being bound to other elements (or helium itself), the neutral helium chooses the "isolated" state to keep symmetric structure.
This is the reason why the helium compounds have not been found until now.
In Fig.4 helium model, the two orbits cross at the right angle, which keeps each de Broglie's wave phase stable.
Other angles are not allowed to keep each wave phase independent.
So there are no more space for the third electron to enter in 1S state.
This means that we can explain Pauli exclusion principle correctly using Fig.4 helium model.
By the way, are there any models, which contains three electrons in the orbits crossing perpendicularly ?
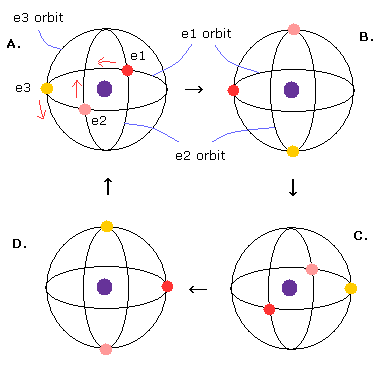
In Fig.21, the three 1S orbits are perpendicular to each other.
This means there are more spaces for the third electron to enter in 1S state ?
This pseudo-lithium model with three same perpendicular orbits of 1 × de Broglie wavelength is impossible.
First, three electrons of Fig.21 are electrically unstable and unbalanced with respect to Coulomb repulsion, because these three electrons are Not located on three vertices of equilateral triangle ( instead, right-angle triangle distribution, which is Not symmetrical distribution of three electrons ).
When three electrons are distributed around the nucleus just on the three vertices of equilateral triangle, these three electrons are just equally distributed around the nucleus, so stable and balanced in terms of Coulomb repulsions, which is Not the case of Fig.21.
(Fig.22) Lengths are different in three 1S orbits.
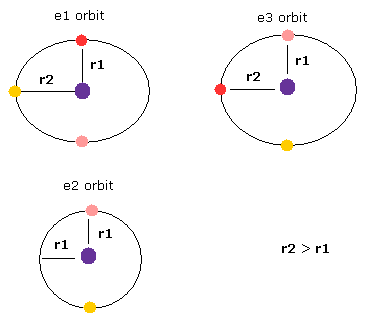
Furthermore, three orbits of Fig.21 are Not symmetrical or same with each other, which means motions of three electrons are chaotic and irregular, Not synchronizing with each other.
If you look at Fig.21 model carefully, you would notice only e2 orbit contains two electrons. (e1 and e3 contains three electrons.)
This means the three orbits of Fig.21 are asymmetric, as shown in Fig.22.
So the time periods are different in them, which is inconsistent with Fig.21.
(This breaks each stable "closed" orbits.)
In conclusion, there are only two stable "symmetrical" orbits in 1S state.

2011/7/23 updated. Feel free to link to this site.