Top page (correct Bohr model including the two-electron atoms)
Electron spin is an illusion !
In this page, we have proved that Schrodinger equation belongs to Bohr Sommerfeld model and furthermore Schrodinger's hydrogen atom is a wrong and unreal thing.
Here we estimate Schrodinger's hydrogen atom more rigorously.
First, Schrodinger himself objected to the concept of the probability density in Schrodinger equation, which is proposed by Max Born.
Schrodinger had a similar idea to Einstein, who strongly objected to the quantum mechanics based on Copenhagen interpretation.
So Schrodinger tried to make new model using "vibrating electrons", but he could not succeed.
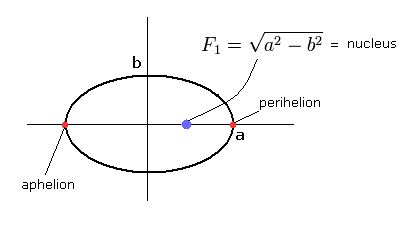
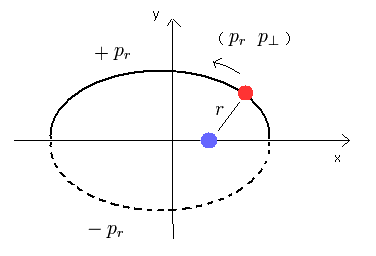
(Fig.1) Bohr-Sommerfeld's "elliptical" hydrogen atom.

In Bohr-Sommerfeld hyrogen model, the relation among the kinetic energy (T), Coulomb potential energy (V) and total energy (E) is
(Eq.1)
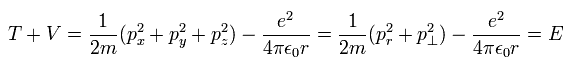
(Of course, this relation is the same as that of Schrodinger's hydrogen atom.)
And "radial" part of Bohr-Sommerfeld quantization conditions is
(Eq.2)
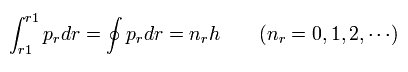
If we suppose the momentum (pr) is
(Eq.3)
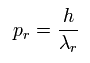
(where λr means "radial" de Broglie's wavelength.)
Eq.2 can be expressed as
(Eq.4)
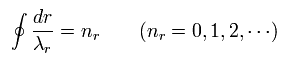
Eq.4 means "radial region" of one orbit is a integer (nr) times de Broglie wavelength.
Here we replace the momentum (pr) by the operator of
(Eq.5)
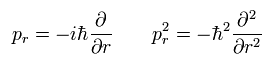
Using the wavefunction (ur) of
(Eq.6)
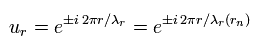
we can get
(Eq.7)
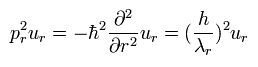
Eq.7 is equal to Eq.3.
And Eq.6 means the wavefunction, which wavelength is λr.
Usually, the momentum (pr) or λ changes at each r, so the wavelength λr is the function of coordinate r.
We can suppose that when a region is very short, its wavelength λ (of Eq.6) is constant in it.
So Eq.4 can be divided into short segments, as follows,
(Eq.8)
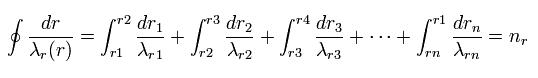
From the relation of Eq.1, we can confirm that the hydrogen's electron belongs to only one plane (for example, x-y plane.)
(Fig.2) Hydrogen's electron belongs to only one plane.
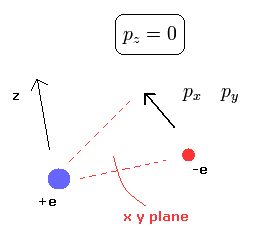
If we define the x-y plane, which contains the electron's momnetum vector at some point and the nucleus, the z component (pz) of the momentum becomes zero.
(At every point, we can define the x-y plane like this.)
(Eq.9)
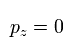
In Fig.2, the Coulomb potential energy (V) is
(Eq.10)
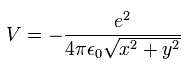
So the gradient in the z direction of the potential energy becomes zero, as follows,
(Eq.11)
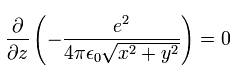
This means the kinetic energy in the z direction is conserved.
The initial value of the z component of the momentum is zero, so the hydrogen's electron always belongs to only x-y plane.
(Schrodinger's hydrogen violates this basic rule a little, which is explained later.)
The x and y directions in one plane can be replaced by "radial" and "tangential" directions.
(Of course, even in 3 dimensional system, it can be divided into radial and tangential parts.)
The remaining quantization condition is
(Eq.12)
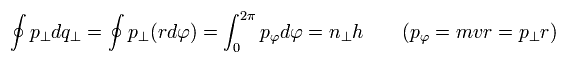
If we replace the "tangential" momentum by "tangential" wavelength, Eq.12 becomes
(Eq.13)
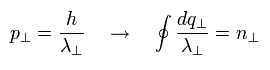
Here we use the tangential wavefunction of
(Eq.14)
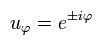
Eq.14 means one round "tangential" orbit is one wavelength.
So in the orbit which radius is r, one round tangential orbit is one wavelength of
(Eq.15)
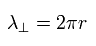
Using the wavefunction of Eq.14 and the tangential momentum operator, we get
(Eq.16)
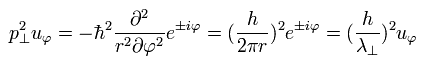
So Eq.15 is satisfied.
As a result, Eq.1 of "classical" Bohr-Sommerfeld relation can be expressed using the wavefunction and momentum operators, as follows,
(Eq.17)
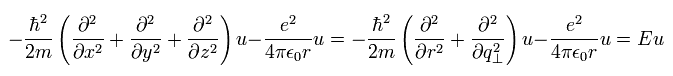
The form of Eq.17 is the same as Schrodinger equation.
In both Bohr-Sommerfeld and Schrodinger equation, the wavefunctions can be divided into the "radial" and "tangential" parts, which are perpendicular to each other.
There is only one total energy (E) value, which satisfies the above three conditions (Eq.1, Eq.4 and Eq.13), as follows,
(About the detailed calculation method, see this page.)
(Eq.18)
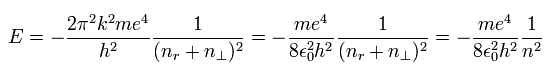
where
(Eq.19)
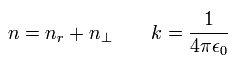
The energy solution of Eq.18 is just same as Schrodinger's hydrogen.
Next we explain why there is only one energy value, which satisfies the above three condition (Eq.1, Eq.4 and Eq.13).
From Eq.1, radial kinetic energy is
(Eq.20)
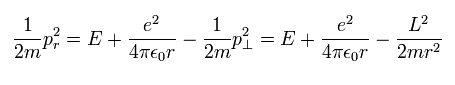
So the radial momentum (pr) is
(Eq.21)
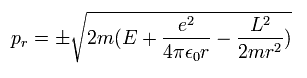
The square value of total angular monetum (L2) is conserved both in Bohr-Sommerfeld and Schrodinger hydrogens.
In Bohr-Sommerfeld model, the value of L2 is gotten from the quantization condition of Eq.12 (or Eq.13).
Also in Schrodinger's equation, "constant" total angular momentum L of L(L+1) is determined by the condition of Eq.12, which is explained later.
And Eq.21 contains the radial condition of every r.
Unknown constant value E can be determined by inserting Eq.21 into the remaining quantization condition of Eq.2 (or Eq.4)
So we can determine only one total energy E value of Eq.18, based on three equations (Eq.1, Eq.4 and Eq.13).
From Eq.21, the radial momentum ( pr ) at each r is determined when E and L2 are conserved.
(This means "radial wavefunction" is determined in both Bohr-Sommerfeld and Schrodinger hydrogen atoms.)
And the momentum (or wavefunction) is "continuous".
Of course, the tangential momentum is determined, as follows,
(Eq.22)
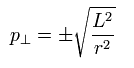
From Eq.21 and Eq.22, the momentum vector at each r is decided.
In the bound state, the electron which is going away from the nucleus needs to turn back.
Considering these facts, the hydrogen's orbit is "closed", as shown in Fig.3.
(Fig.3)
Schrodinger equation of the hydrogen atom is
(Eq.23)
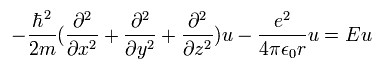
which is the same as Eq.17.
In the Schrodinger equation, we use the polar coordinate of
(Eq.24)
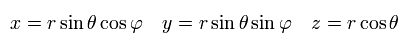
For example, the partial differentiation by x can be expressed as
(Eq.25)
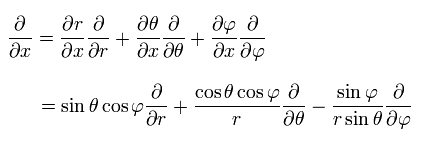
So Eq.23 is equal to
(Eq.26)
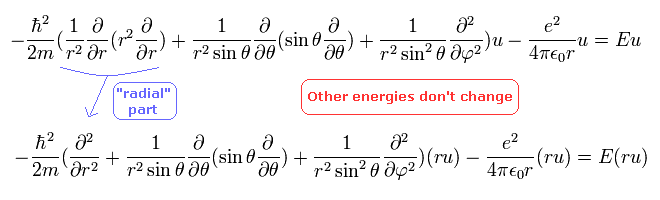
in the second line, we use "ru" instead of "u" as the wavefunction, which makes "radial part" simpler form.
The wavfunction "ru" is divided into "radial" and "tangential" parts, as follows,
(Eq.27)
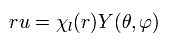
Inserting Eq.27 into the second line of Eq.26, and dividing Eq.26 by
(Eq.28)
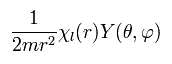
we get
(Eq.29)
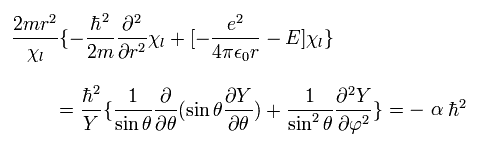
where α is a constant.
From Eq.29, we can divide Eq.26 into "radial" and "tangential" equations of
(Eq.30)
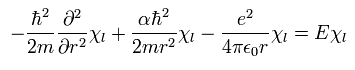
and
(Eq.31)
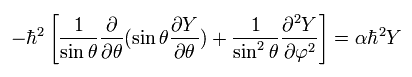
From Eq.26, we pick out the tangential kinetic energy of
(Eq.32)
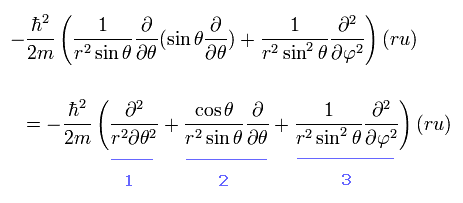
We can easily understand that number "1" term of Eq.32 is the kinetic energy in the θ direction.
And number "3" term of Eq.32 is the kinetic energy in the φ direction, when θ is fixed at 90 degrees, as shown in Eq.33
(Eq.33)
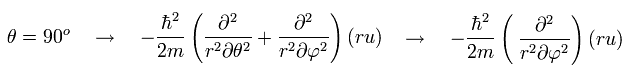
When θ is fixed at 90 degrees, the "strange" number "2" term of Eq.32 vanishes. ( cos 90o = 0)
To compare with Bohr-Sommerfeld model, it is better that we choose only one plane in Eq.17 or Eq.23.
The variable θ is unsuitable for this purpose, as shown in Eq.32.
The variale φ is suitable, but we need to fix θ at 90 degrees. (Eq.33.)
(Fig.4)
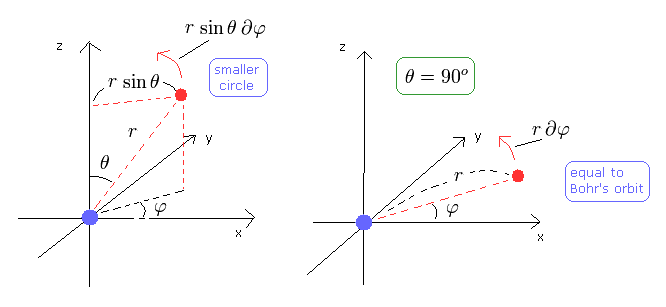
The left panel of Fig.4 is the case where θ is not 90 degrees.
In this case, the circle in the φ direction becomes smaller than the Bohr's orbit, and kinetic energy in the φ direction is smaller, too.
To make up the deficit, the number "2" term of Eq.32 becomes important when θ is not 90 degrees.
So we consider the case where the angular momentum in the z direction is the maximum in each l. (For examle, l=2, m=2 ).
(Eq.34) The cases of ( l=1, m=1 ) ( l=2, m=2 ), and ( l=3, m=3 ).

In these cases of Eq.34, the hydrogen's orbit should belong to x-y plane.
So basically, the variable θ must not be included in these spherical harmonics.
But Schrodinger equation neglects this fact, which makes the square value of the total angular momentum a little bigger. ( = L(L+1) ).
(Though it is quite natural that the square value of L becomes L2, like Bohr-Sommerfeld model.)
In Eq.34, we substitute θ = 90 degrees into the solution of Schrodinger equation.
Of course, if we substitute θ = 90 degrees into Eq.31 of Schrodinger equation before getting the solution, we arrive at the same results, as follows,
(Eq.35)
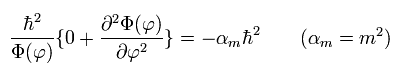
(Eq.36) Solution of Eq.35.
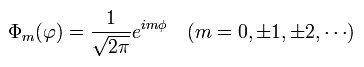
The same results of Eq.34 and Eq.36 can be gotten also from Bohr-Sommerfeld model, which orbit we suppose belongs to x-y plane.
(In this case, we suppose the solution u of Eq.17 is the function of x and y (not z).)
As a result, when the quantization condition of Eq.34 is satisfied, it means one of Bohr-Sommerfeld quantization conditions is satisfied.
(So one of three importatnt conditions which determine the energy value proves to be common in Schrodinger and Bohr's hydrogens.)
Even when the angular momentum vector points to other directions, the "tangential" kinetic energy is common in the same l.
So when one of these states is equal to Bohr-Sommerfeld condition, it applies to other states, too.
Also in Bohr-Sommerfeld hydrogen, there are various patterns in which the angular momentum vectors point to various directions.
Of course, they have the common energy value.
And it is the easiest way that we consider the orbit, which belongs to x-y plane as a representative.
For example, in the case of l=2, the solutions of spherical harmonics always contain sin2θ or cos2θ, which is two de Broglie's wavelength in the θ direction.
But as I said, the θ variable is a little complicated, which is different from φ direction.
Number "1" term of Eq.32 gives "original" angular momentum (and tangential kinetic energy) in the θ direction.
But Eq.32 includes "artifact" (= number "2" term) even when the hydrogen's solution doesn't have φ variable (m=0).
This causes the strange phenomenon in which the square value of the total angular momentum is L(L+1) instead of L2.
Originally, we need to erase the number "2" term of Eq.32, when m = 0. (But again Schrodinger equation neglects this fact.)
Schrodinger's solution χ (= rR ) contains "radial" kinetic energies (= Tr ) as shown in Eq.30 or Eq.37.
(Eq.37)
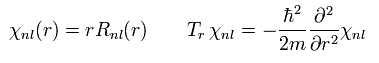
These Schrodinger's solutions are
(Eq.38)
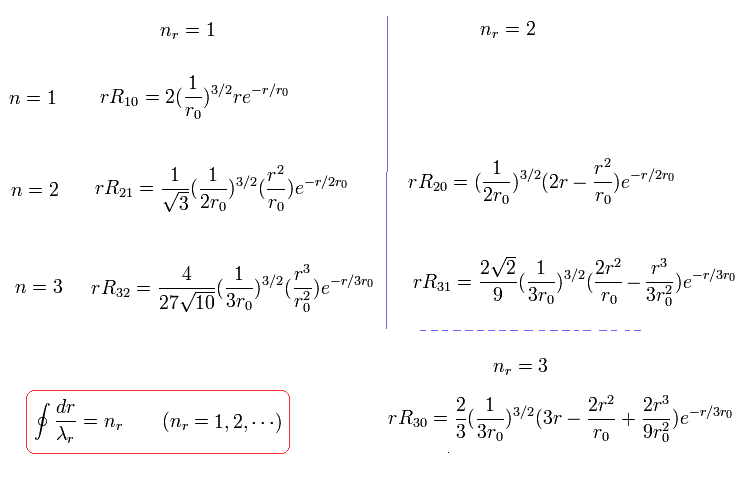
where r0 is "Bohr radius".
For example, when nr = 1, which means the amount of "radial" kinetic enegy is "1", one round orbit in the "radial" direction is one de Broglie's wavelength, as follows,
(Eq.39)
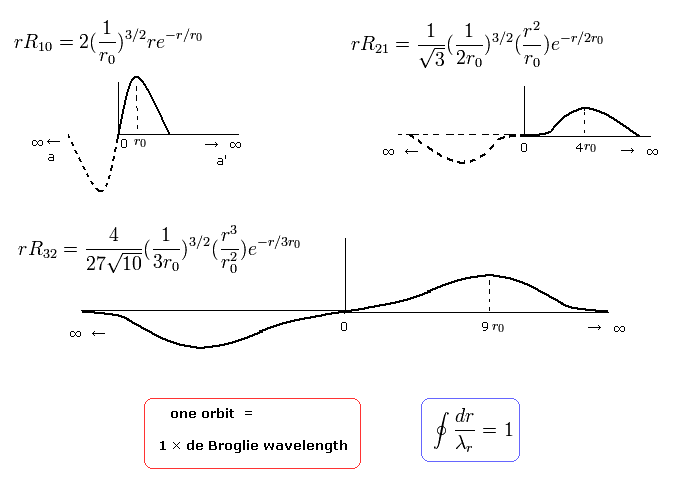
These are what we call "wave phases", which satisfy de Broglie's relation.
when nr = 2, which means the amount of "radial" kinetic enegy is "2", one round orbit in the "radial" direction is two de Broglie's wavelength, as follows,
(Eq.40)
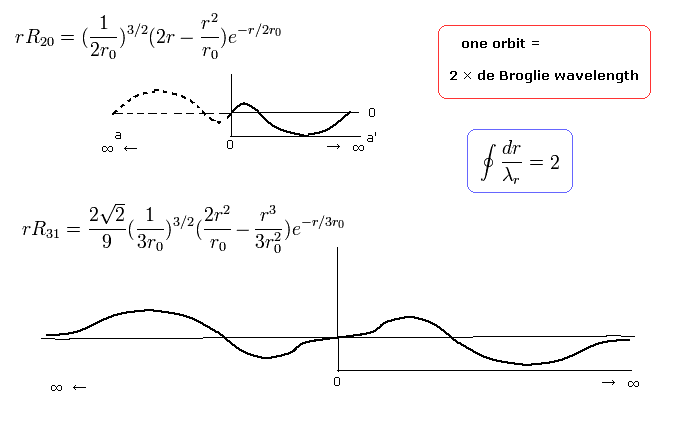
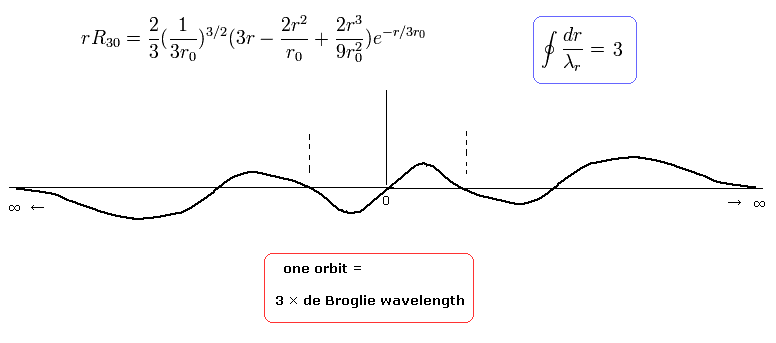
when nr = 3, which means the amount of "radial" kinetic enegy is "3", one round orbit in the "radial" direction is three de Broglie's wavelength, as follows,
(Eq.41)
From Eq.34 and Eq.38, we can get the energy levels, which are the same as Bohr-Sommerfeld model of Eq.18.
For example, in the energy level of n=1, Shorodinger's solution doesn't have the angular momentum (l=0), but has the "radial" kinetic energy ( nr= 1, ).
On the other hand, in the n =1 Bohr-Sommerfeld model, the angular momentum is 1 (l=1), and "radial" kinetic energy is zero ( nr = 0 ).
As a result, the sum of them becomes 1 in both cases ( n = 1 + 0 = 0 + 1 = 1 ), according to Eq.18 and Eq.19.
(Eq.18)
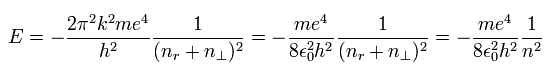
where
(Eq.19)
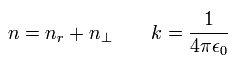
So the energy levels in both Schrodinger's and Bohr-Sommerfeld's hydrogens are the same with the same n. (Eq.42)
(Eq.42) Schrodinger = Bohr-Sommerfeld.
Next we try to prove that the radial quantization conditions are the same in Both Schrodinger and Bohr-Sommerfeld model.
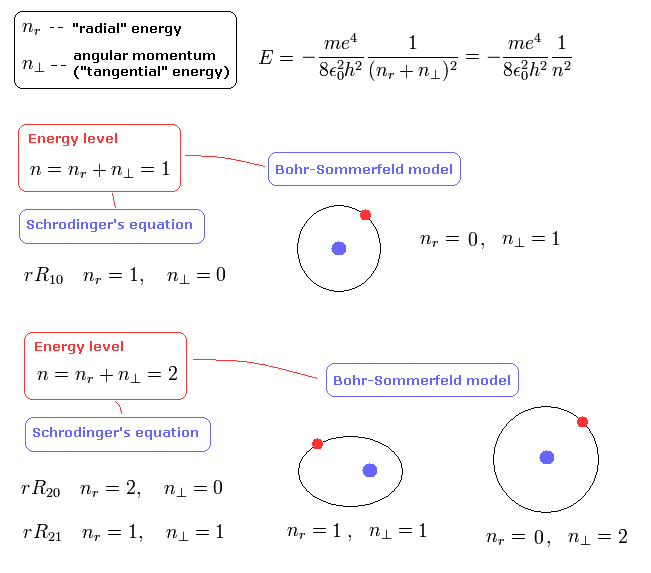
(Fig.5) "Radial" de Broglie's wave (= phase).
In the upper panel of Fig.5, a half of the orbit in Bohr-Sommerfeld model contains 0.5 "radial" de Broglie's wave.
(So one round orbit contains 1 × "radial" de Broglie's wave. (= 1 de Broglie wavelength in the radial direction.))
a1 and a2 are perihelion and aphelion, respectively, as shown in Fig.6.
(Fig.6) Sommerfeld's 2S "elliptical" orbit (upper panel of Fig.5).
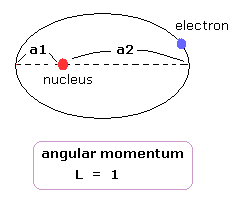
So the upper panel of Fig.5 state can be expressed as
(Eq.43)
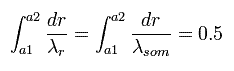
As shown in Fig.6 at the perihelion and aphelion, the "radial" momentums become zero, which means the de Broglie wavelength is infinite.
So at the ends of the upper panel of Fig.5, the slope is zero (= λ is infinite.)
In fact, by change of variables, we can prove that the upper panel of Fig.5 (=Sommerfeld's model) is equal to the lower panel of Fig.5. (= Schrodinger's solution.)
Here we explain about this.
In Eq.43, we change the variable r into r', as follows,
(Eq.44)
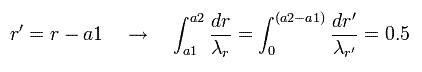
Eq.44 means "translation" of Eq.43.
Next we change the variable, as follows,
(Eq.45)
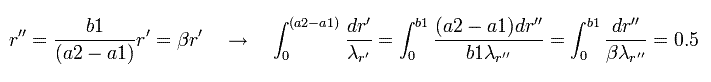
And changing r'' into r,
(Eq.46)
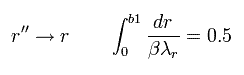
where β is "arbitrary" value.
Eq.45 means the enlargement or reduction of the figure itself.
When β is infinite, as follows,
(Eq.47)
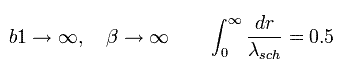
Eq.47 expresses the lower panel of Fig.5 (= Schrodinger's "radial" solution.)
This means the Bohr-Sommerfeld "radial" quantization condition is just equal to Schrodinger's solution in Fig.5.
To be precise, we need to divide the Sommerfeld's radial orbit into the short segments, and translate and enlarge each segment properly.
In this method (= change of variables, see Fig.7), we can prove Bohr-Sommerfeld quantization conditions are equal to those of Schrodinger's equation. (Fig.7)
(Fig.7) Change of variables.
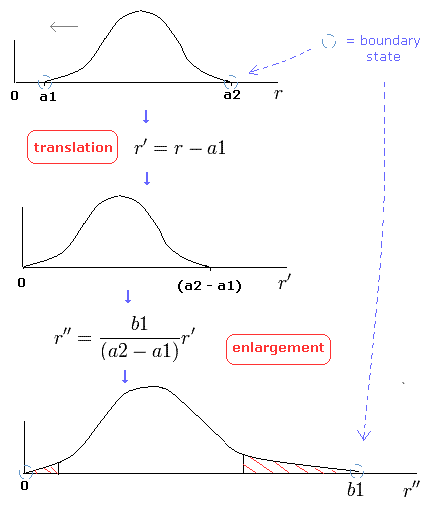
But there is one point which we have to pay attention to.
Only at the ends of Sommerfeld's "radial" wave phase of Fig.5, the wavelength is infinite, which means the radial momentum is zero at the ends.
(See Eq.48 or "boundary" state of Fig.7.)
We can not change these "infinite" wavelength into some "finite" wavelength by the above method such as translation and enlargement (or reduction). (See Eq.49.)
(Eq.48) At both ends, the wavelength is infinite.
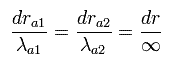
(Eq.49) We can not change boudary states.
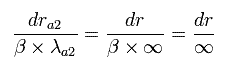
So to get the same energy value, the bounary states in both Sommerfeld's and Schrodinger's wavefunction need to be the same. (Fig.7).
Fortunately, all boundary states of Schrodinger radial wavefunctions have infinite wavelength, as shown in Eq.39 and Eq.40.
The exceptions are 1S (rR10), 2S (rR20), and 3S (rR30) states.
In these states, the angular momentum is zero (l=0), so the radial momentum is infinite at the origin.
(The momentum is in inverse proportion to a square root of r, so its slope is finite value, which is not zero.)
If Bohr-Sommerfeld model has this angular momentum zero orbits (which means "oscillating" instead of rotating), these states would be just the same as those of Schrodinger's "S" wavefunctions.
Because both of them satisfy the same energy relation.
(Of course, the angular momentum zero state is "unreal", because the electron collides with the nucleus.)
As a result, Schrodinger's wavefunction satisfy the three conditions of Eq.1, Eq.2, and Eq.12, which is the same as Bohr-Sommerfeld's ortbis with the same energy.
-----------------------------------------------------------------------
By the way, can we express Sommerfeld's "radial" de Broglie's wave phase of Fig.5 by another figure ? (Fig.8 red line.)
(Fig.8) Sommerfeld's wave phase.
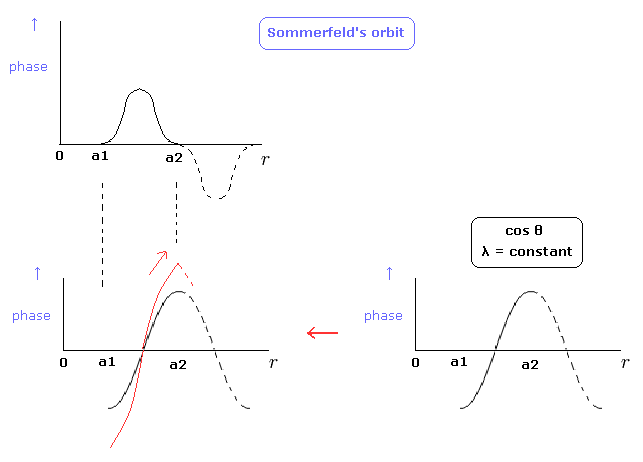
In the lower panel of Fig.8, the slopes at the points of a1 and a2 are not zero.
"Original" cosine curve has the zero slope, so to make λ at these points infinite, the slope must not be zero.
So the slople at these points are discontinuous, which means wave phases change becomes infinite.
As a result, we can not choose the lower panel of Fig.8 as Sommerfeld's radial wave phase.
------------------------------------------------------------------------
We explain why Schrodinger equation is wrong in this page.
Again we summarize these reasons.
(Fig. 9) Schrodinger's 2P "radial" wave function (angular momentum = 1).
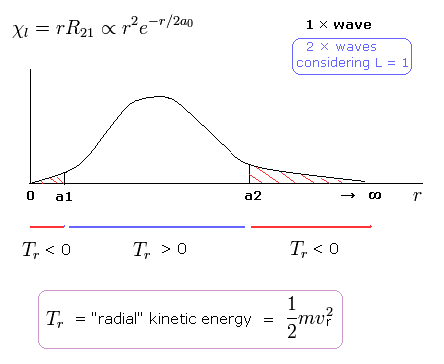
As shown in Fig.9, the 2P "radial" wave function ( χ = rR21 ) contains the regions of the minus kinetic energy ( r < a1, a2 < r ).
In the "real" Bohr-Sommerfeld model, the electron's orbital radius (r) can not be shorter than some "minimum" value ( a1 ), when the angular momentum is not zero (Fig.6).
(When the angular momentum is zero, the electrons is oscillating, and the r can be "theoretically" close to zero.)
But the probability density of the Schrodinger equation must be from zero to infinity.
Strange to say, in the region of ( r < a1 ), the "radial" kinetic energy becomes minus ( 1/2 mv2 < 0 ! ) in the Schrodinger equation.
Also in the Schrodinger equation, Kepler's law of the constant areal velocity is satisfied, which means the angular momentum (L) is constant (L = 0, 1, 2, ..) in each orbital.
So the "tangential" kinetic energy can not be minus. Instead, "radial" kinetic energy beomes minus in some region (Fig.9).
(Because, the "tangential" kinetic energy becomes closer to infinite, as r is closer to zero.)
When the r is bigger than a2, the Coulomb potential energy becomes higher than some maximum value.
In this region, to keep the total energy (E < 0) constant, the "radial" kinetic energy must be minus !
These unreasonable and unreal states shows that Schrodinger equation is wrong.
But why we have to make probability density regions of Schrodinger's atoms from zero to infinity ?
For example, in the Helium atom, Schrodinger's variational method can not give the "concrete" orbital image, so the boudary states can not be known.
So by a convenient means, we set the probability region from zero to infinity.
It causes "unreal" states such as 1S, 2S , and 3S, which have zero angular momentum.
If the radial wavefunction is constant, that constant must be zero to prevent divergence when integrating the probability density in all space.
So Schrodinger's wavefunction always needs to include radial wavefunction, which is not constant.
As a result, in the n=1 energy state, nr need to be 1 instead of the angular momentum.
You can not make "actual" electron's moving region smaller than the above region from zero to infinity in Schrodinger's hydrogen.
In this case, "radial" wave phase becomes discontinuous on the way.
So the Schrodinger's electron needs to move from zero to infinity, and return !

2011/7/10 updated. Feel free to link to this site.