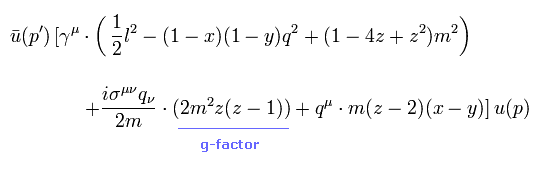
Top page ( quantum mechanics is false. ← 6/30/2024 )
Strange "spin" is NOT a real thing
Special relativity is wrong !
Detailed calculation of anomalous magnetic moment in QED.
The high precision tests of quantum electrodynamics (QED) supports the present quantum theory, though the quantum mechanical world is very strange.
As you know, the anomalous magnetic moment (g-2) is the most accurate QED test.
But in fact, QED calculations depends on wrong mathematics ! ( See this page. )
And if special relativity is wrong, QED is wrong, too.
Lamb shift is "vague" and difficult to measure to high-order.
( And Lamb shift calculation in QED uses various "ad hoc" methods to match the experimental results.)
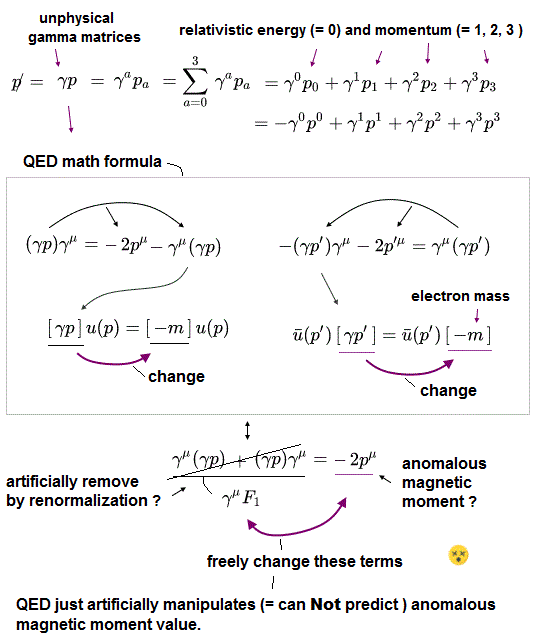
In this page, we show that the anomalous magnetic moment values can be manipulated artificially.
Basically, if you use simple Dirac equation ( free particle, mass shell ) and γ matrices, you can control the g factor value.
This page deals with the electron. But if you change the mass, you can apply these methods to other particles' g factors.
(Eq.1) Standard g-factor.
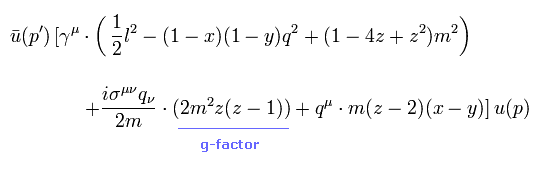
(Eq.2) Manipulated g-factor !
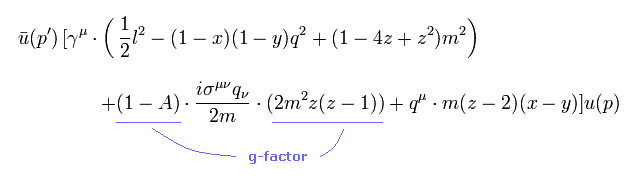
The blue line of Eq.2 is a manipulated part of g factor ( the value "A" can be arbitrary ).
As a result, g factor can be manipulated artificially.
As shown in this page (Eq.5-12), Dirac equation of free particle (= mass shell ) is
(Eq.3)
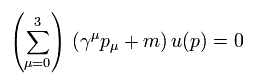
When the same index (= μ) is used twice in one term, this means the sum of four vectors (0-3).
And here the natural unit of ħ = 1, c=1 and ( -1, 1, 1, 1, ) version metric tensor is used.
So Dirac equation can be expressed as
(Eq.4)
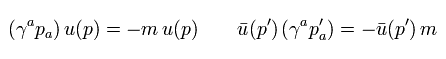
where we sum from 0 to 3 with respect to the index "a".
As shown in appendix, Dirac gamma matrices satisfy
(Eq.5)
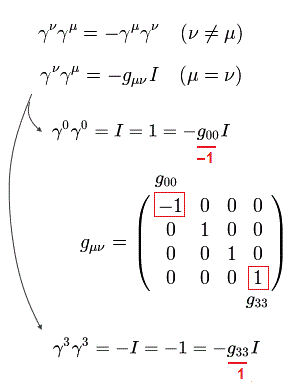
Eq.5 means
(Eq.6)
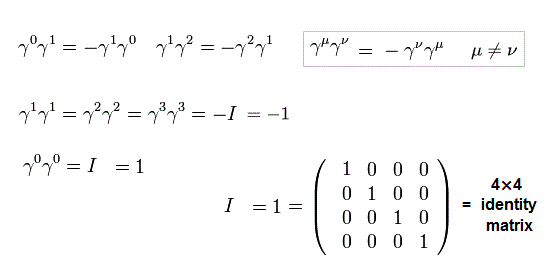
For example, γ0γ0 = I ( = 4× 4, identity matrix ),
(Eq.7)
And γ matrices satisfy anticommutation relation like,
(Eq.8)
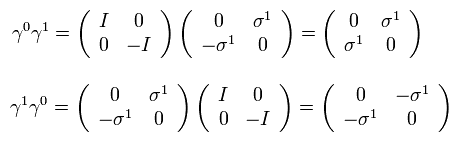
Using the relation of Eq.5, Dirac equation of Eq.3 proves to be equal to Klein-Gordon equation.
(Eq.9)
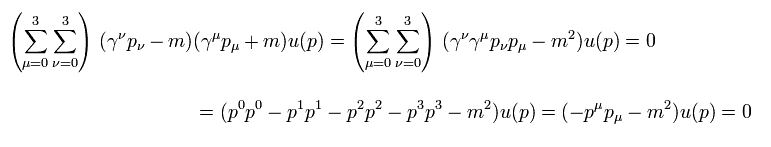
This webpage uses ( -1, 1, 1, 1 ) metric tensor.
Due to the anticommutation relation of gamma matrices, other terms vanish.
As shown in this page, the following relation among two electrons ( in and out ) and one photon is used here.
(Eq.10)
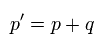
Satisfying Eq.10 and Eq.4 means this photon is virtual photon, which does NOT obey Einstein mass shell condition.
So this virtual photon q is tachyon.
Like Eq.9, Dirac equation of Eq.4 is just equal to Kelin-Gordon equation of
(Eq.11)
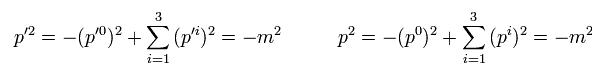
Each electron ( p' and p ) satisfies Einstein energy and momentum relation.
From Eq.10 and Eq.11, we obtain
(Eq.12)
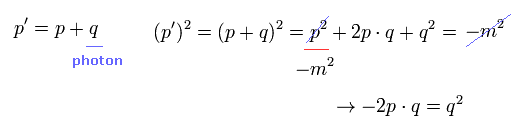
In QED g-factor calculation, we MUST choose q2 = 0 (= photon mass is zero ) to get g-factor value.
So "pq" is also zero,
(Eq.13)
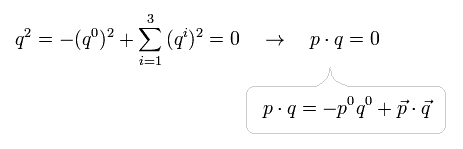
where "pq" also means Einstein's formula.
In this case, electron and virtual photon satisfy Einstein mass shell, like
(Eq.14)
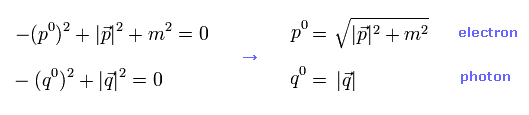
So "pq" can be expressed as
(Eq.15)
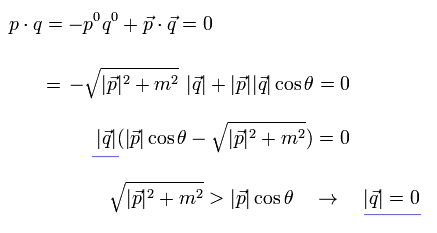
From Eq.15, all components of "q" becomes zero, so p' = p.
(Eq.16)
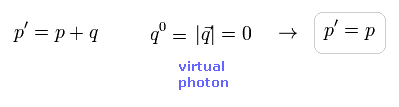
In these very easy conditions (= virtual particles satisfy mass shell ), QED can manipulate various values also in other things.
In the next section, we explain this fact clearly.
So law of "nature" does NOT obey QED to determine various values.
Because if law of nature obeys QED, g-factor MUST be deterimined at a single value.
( And QED violates basic math rules. )
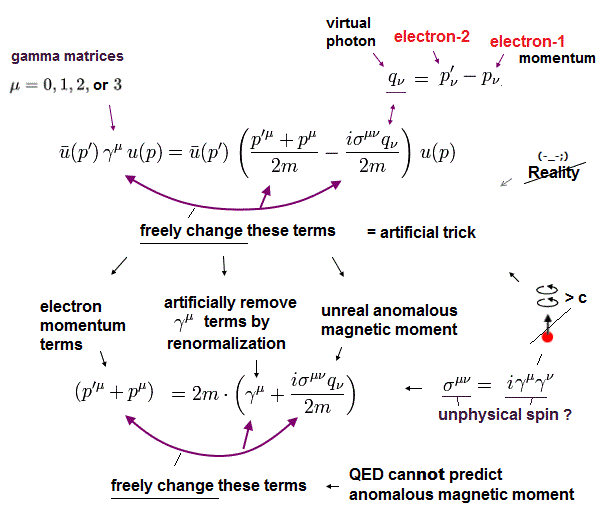
In addition to usual Dirac equation, we use the key relation of
(Eq.17)
Eq.17 is very important when we try to transfer excessive values of g factor to the γ vertex part and artificially remove them.
For exmaple, when μ of Eq.17 is zero,
(Eq.18)
Using the relations of Eq.5 and Eq.6, the left side of Eq.18 is
(Eq.19)
where the anticommutation relation is used.
Eq.19 is equal to
(Eq.20)
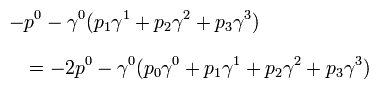
where
(Eq.21)
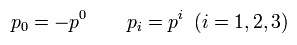
As a result, we can prove Eq.18.
( In the same way, Eq.17 proves to be true. )
As shown in this page, we get
(Eq.88)
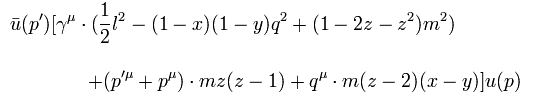
If we use the following relation in Eq.88, we get Eq.1.
(Eq.22)
So the most important is the change in the term of
(Eq.23)
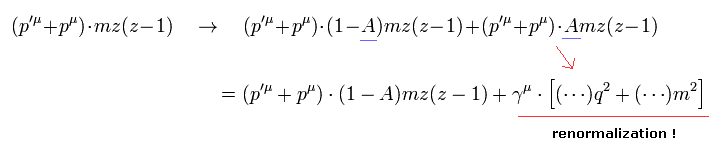
where the value "A" can be arbitrary.
If we can do the manipulation of Eq.23, the g factor can be changed as we like.
( q2=0 and the renormalization of γ term. )
Using the important relation of Eq.17,
(Eq.24)
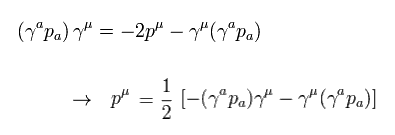
we have
(Eq.25)
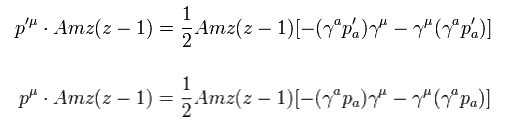
Using the usual Dirac equation of Eq.4,
(Eq.4)
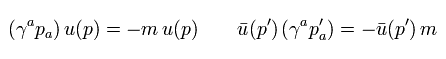
the first term of the upper equation in Eq.25 is
(Eq.26)
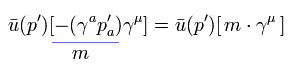
(Eq.27) Transfer p' of right side to left side.
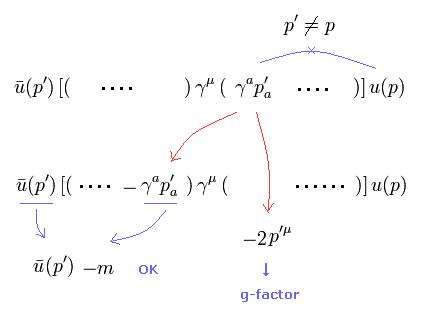
In Eq.27, when p' is at the right, it cannot be changed into -m using Eq.4.
So they transfer p' to the left side and change it to -m.
Also in this process, one of the g-factor is generated.
But when the virtual photon q = 0, as shown in Eq.16, we can change it to "-m" freely without transferring it,
(Eq.28)
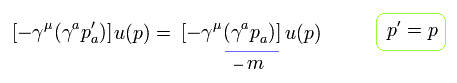
As a result, we can change all terms of Eq.25 upper into " γμ m " terms.
This means we succeeded in manipulating g-factor.
(Eq.29) Virtual photon q = 0 → g-factor can be manipulated freely.

In the same way, we can change the lower terms of Eq.25 into " γμ m " terms.
As a result, we can change the original equation like
(Eq.30)
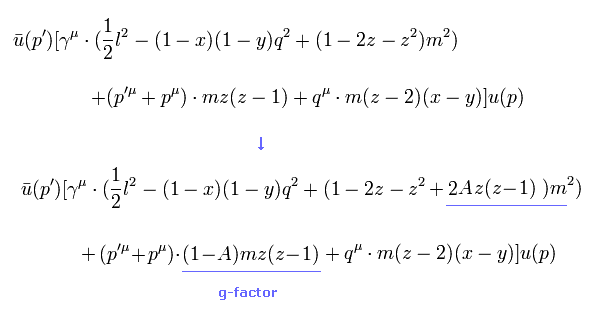
Using the replacement of Eq.22 in Eq.30, we obtain the manipulated g-factor of Eq.2.
(Eq.2) Manipulated g-factor !
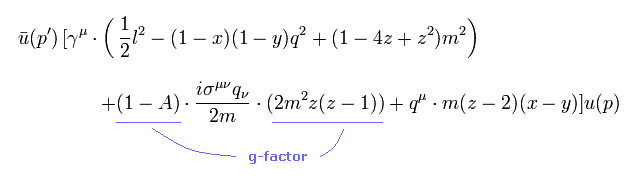
The important key player is "virtual photon", as shown in this page.
( Of course, the moment virtual photon appears in g-factor, QED itself is wrong, because it disobeys relativity. )
(Fig.1) p' = p + q. ( q = 0 )
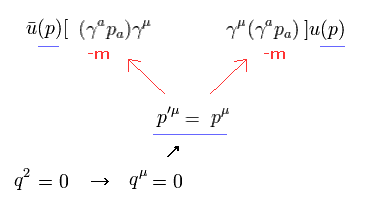
As shown in Fig.1, if q = 0, the difference between p' and p is gone.
So, both left (p') and right (p) sides become "p", and g-factor can be easily changed.
And vertex (spin) correction value of Eq.1 is used also in one part of Lamb shift.
So Lamb shift value cannot be fixed at a single value.
( Though Lamb shift calculation by QED is much more artificial and complicated. )
As shown in this page.
(Eq.99)

(Eq.100)
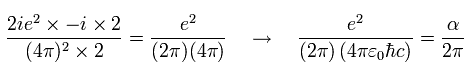
(Eq.103)
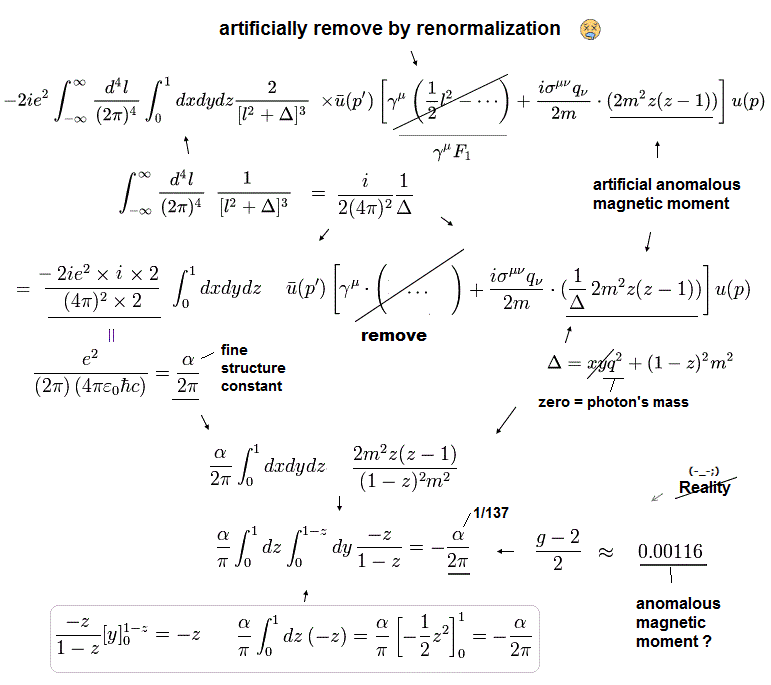
(Eq.107)
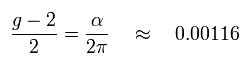
So in Eq.2, this value of Eq.107 becomes 0.00116 × (1-A) !
This A can be arbitrary.
Of course, in every order level, "Bohr magneton" is used, this manipulation is possible.

2012/9/9 updated. Feel free to link to this site.