Top page ( quantum mechanics, Einstein relativity is wrong )
QED is false.
Particle physics, QCD is false
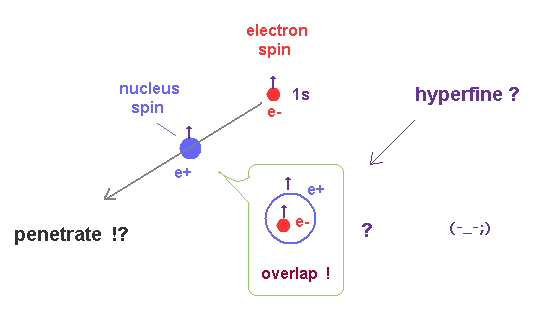
(Fig.1) Quantum mechanical unrealistic interpretation of tiny hyperfine structure energy splitting ↓ = an electron must penetrate a tiny nucleus !?

Hyperfine structure is a tiny atomic energy levels' splitting (= only about 5.9 × 10-6 eV splitting ) allegedly caused by magnetic interaction between nuclear (or proton ) tiny magnetic moment and electron's spin.
But first of all, the electron spin is unrealistic, Not actual spinning.
Second, quantum mechanical interpretation of this tiny hyperfine structure needs the unrealistic assumption that an electron with (fictitious) spin must penetrate or get inside a tiny proton or nucleus to generate this small energy splitting.
Quantum mechanical hyperfine structure is said to occur only when an electron is at the position of a nucleus or proton (= |ψ(0)|2, r = 0, this p.2, this p.3, this p.2 ) in hydrogen 1s ground state that has No orbital angular momentum ( l = 0 ) where an electron must always unrealistically crash into or penetrate the central nucleus, which is impossible.
(Fig.2) QED contradicts experimental results.
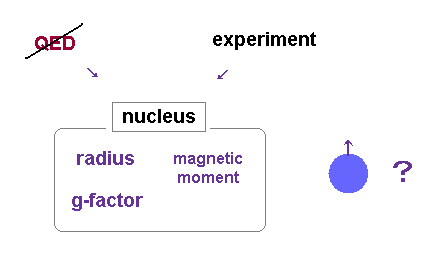
It is known quantum electrodynamics (= QED ) cannot handle any nuclear phenomena (= imaginary quark, gluon strong force ) such as nuclear spin (= hyperfine structure ) and nuclear mass.
So physicists created an ad-hoc quantum chromodynamics (= QCD ) with unreal imaginary time, which cannot obtain analytical nuclear values, and QCD also depends on many freely-fitting parameters with No power to predict any physical values.
So in the hyperfine energy splitting and nuclear (or proton ) spin's magnetic momnet (= or g-factor ), physicists have to use experimentally-observed values instead of obtaining them from (useless) quantum mechanical theory.
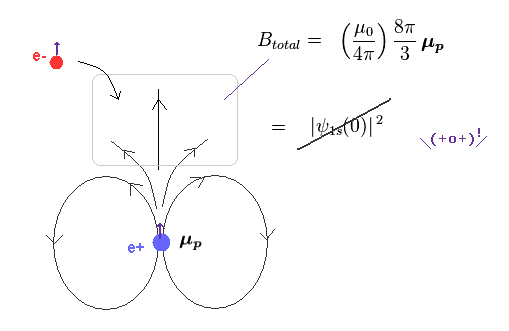
(Fig.3) Fermi contact accounts for the leading order of hyperfine structure.
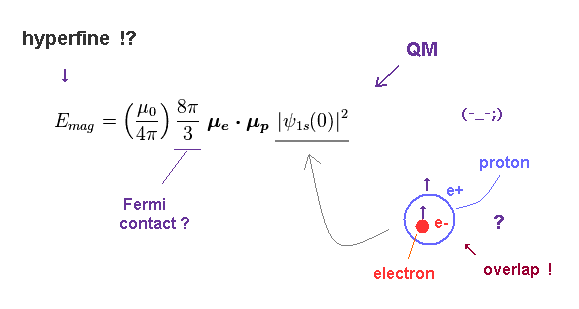
It is said that Fermi contact interaction is the main cause of hyperfine structure where an electron must unrealistically penetrate and enter a tiny proton or nucleus ( this p.19-left, this 4.1.5 ).
The important point is that this Fermi contact value used in quantum mechanical hyperfine structure was derived by semi-classical model (= though unrealistic assumption of electron penetrating the nucleus and fictitious spin is needed, this p.10-2nd-paragraph ), Not by quantum mechanics
In Fig.3, μe and μp are magnetic moments of electron and proton.
The probability of ψ(0) means 1s electron can interact with nucleus only when it exists inside proton !
The problem is how this 8/3 π coefficient is obtained.
Unfortunately, there are NO convincing reasons for this value, as I say later.
(Fig.4) Quantum mechanics (QM) argues magnetic field exists only inside proton !
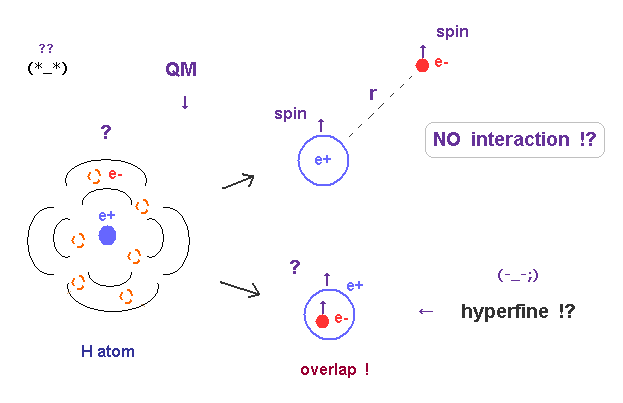
The reason why quantum mechanics unrealistically insists hyperfine structure or very weak nuclear-electron spin magnetic interaction happens only inside the tiny proton or nucleus is that this (fictitious) spin magnetic interaction vanishes when an electron is outside of a nucleus.
As shown in this page ① and ②, the magnetic interaction between a nuclear spin and an electron spin becomes the opposite, positive or negative depending on an electron's position outside the nucleus.
When an electron with up (or down ) spin spreads in spherically symmetric way like in hydrogen's s orbital, the magnetic dipole-dipole interactions between nuclear spin and electron spin (= outside the nucleus ) consist of the opposite plus and minus energies (= total zero ), because the magnetic field caused by the spin going around and returning to the original position have the same amount of the opposite up and down (or left and right ) directions
This means the total magnetic interaction between the nuclear and electron spin-spin magnetic interaction is canceled out to be zero ( this p.10-last-paragraph, this p.1-(5.3)-p.2-upper ), when the electron is outside the nucleus.
↑ This shows quantum mechanical hyperfine structure is wrong due to its violation of energy conservation law.
Because when an electron is outside the nucleus, there is no energy difference depending on electron spin (= nuclear electron spin-spin magnetic interaction is canceled out to be zero outside the nucleus ).
And only when the electron (unrealistically) enters the tiny nucleus, the nuclear-electron spin-spin magnetic interaction suddenly occurs and splits the energy levels depending on electron's spin up or down direction.
↑ If the total energy is conserved, if there is no energy splitting outside the nucleus, there should be No energy splitting also inside the nucleus (= hence, No hyperfine energy splitting ), because electron's kinetic energy should cancel the mangetic interaction or potential energy difference to conserve the same constant total energy.
It means quantum mechanical hyperfine structure violating total energy conservation law is wrong and unrealistic.
(Fig.5) Electron spin enters proton → spinning speed is faster than light.
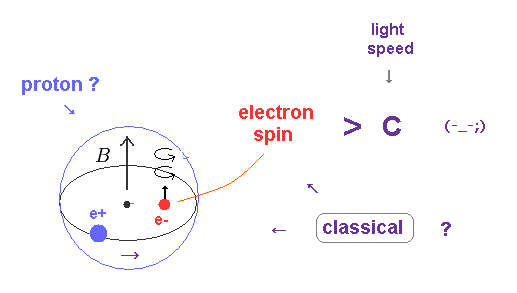
The quantum mechanics argues the whole electron must enter the proton, and interact with proton's magnetic field (= B ).
As shown on this, electron spinning speed becomes 1644 × 108 m/s (= more than 500 times light speed ! ) inside proton !
So the quantum mechanical idea that electron inside proton causes hyperfine structure is unrealistic and impossible.
(Fig.6) Electron's probability at the origin (= nucleus ) is zero.

Electron's probability is given by electron's wavefunction × volume, which volume becomes zero in the point of nucleus.
So quantum mechanical hyperfine structure depending only on the electron at the position of r = 0 (= nucleus ) is unrealistic ( this p.3 ).
(Fig.7) Magnetic field near the origin (= proton ) becomes infinite.
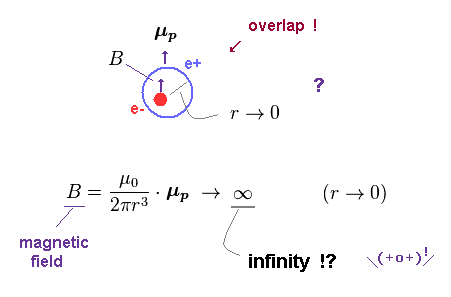
According to this and this page, the magnetic field (= B ) generated by the magnetic moment (= μp ) is inversely proportional to the third power of r (= distance, this p.8(or p.7) ).
When the electron comes near the proton, the distance between them is closer to zero ( r → 0 ).
As a result, their magnetic energy ( field ) diverges to ± infinity ! = Nuclear and electron spin-spin magnetic energy also becomes infinite unrealistically in quantum mechanical hyperfine structure.
(Fig.8) Unrealistic magnetic field in hyperfine structure.
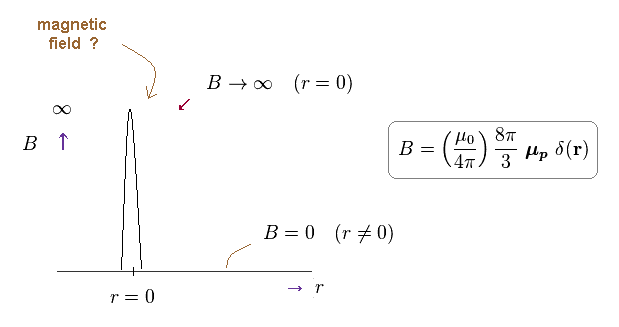
As shown on this site (p.2), the magnetic field in the hyperfine structure is expressed using Dirac delta function (= δ(r) ).
So the magnetic field diverges to infinity at the origin (= nucleus ) !
They argue this infinite magnetic field B can cancel the zero probability of electron at the origin (= Fig.6 ).
Because ∞ (= B ) × 0 (= probability ) at the origin becomes some "finite" value.
As you see, this idea of quantum mechanical hyperfine structure is very ad-hoc and too good to be true.
(Fig.9) Magnetic energy becomes ±∞ only at the origin !?
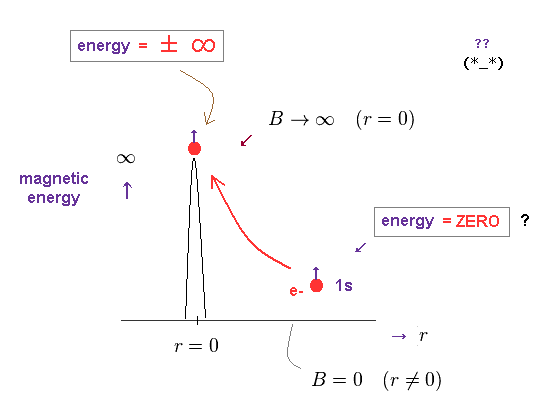
Using the magnetic field (= B ) based on delta function, we can know magnetic energy distribution in the hyperfine state.
Surprisingly, this magnetic energy diverges to ±∞ at the origin.
In all other places (= outside the nucleus ), this magnetic energy always becomes zero !
How this electron can absorb or emit high energy photons depending on its position !? ← Impossible.
↑ And this quantum mechanical hyperfine structure clearly violates the energy conservation law, so false.
Because there is no spin-spin magnetic energy or hyperfine energy splitting outside the nucleus, but only inside the nucleus, the hyperfine energy splitting happens (= violation of total energy conservation law due to its lack of kinetic energy canceling the magnetic potential energy change )
(Fig.10) Magnetic dipole energy becomes 3 × 108 eV inside proton ! Impossible !
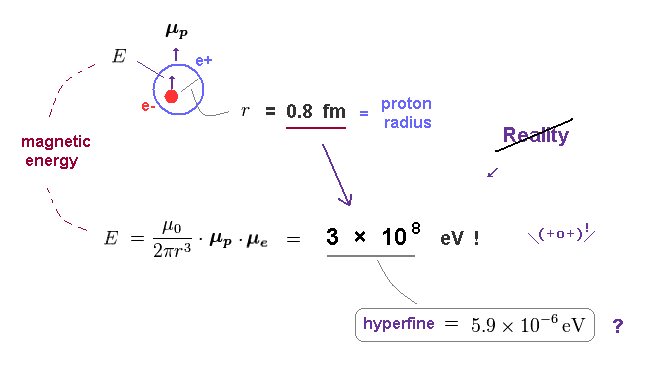
Using the proton's radius (= 0.8 fm = 0.8 × 10-15 m ), the magnetic dipole energy ( see Fig.7 ) becomes as big as 3 × 108 eV inside proton !
It is impossible that such a big magnetic energy (= 3 × 108 eV ) suddenly appears and is given to ( or emitted from ) electron within a range of extremely small hyperfine state (= 5.9 × 10-6 eV )
(Fig.11) 1s hydrogen wavefunction contains Bohr radius (= a0 ).
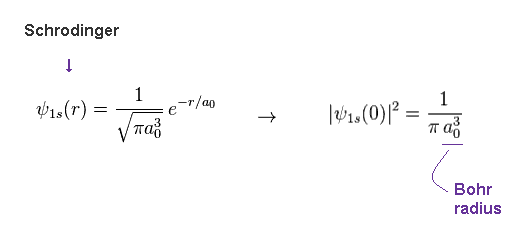
As shown on this site (p.3), the hydrogen 1s wavefunction contains the reciprocal of the third power of Bohr radius (= 1/a03 ).
So, in fact, the probability at the origin possesses the information of the mean distance between electron and nucleus, like classical model of this.
This is the important trick in hyperfine structure by quantum mechanics.
(Fig.12) Magnetic interaction between nuclear spin and realistic electron's orbital motion related to Bohr radius causes actual hyperfine energy splitting.
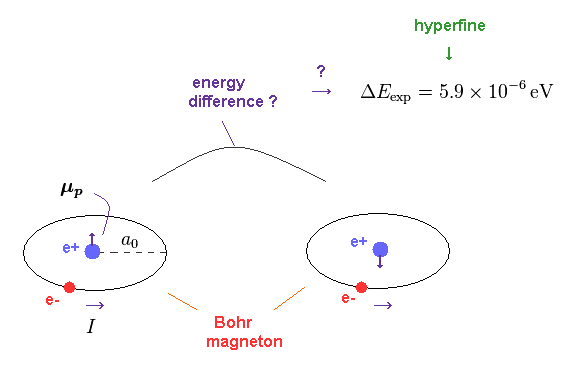
In fact, realistic electron's orbital motion in successful Bohr's atomic model without unrealistic electron spin can reasonably explain the tiny hyperfine energy splitting or nuclear spin-electron's orbital magnetic energy.
(Fig.13)
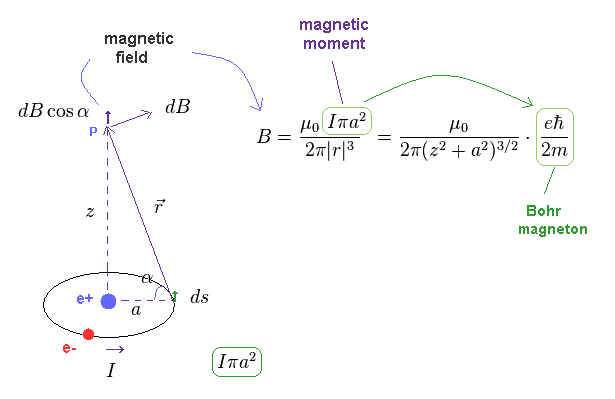
As shown on this page, the magnetic field (= B ) generated by classical magnetic moment (= Iπa2 ) becomes like Fig.13. Magnetic moment is given by the area × current I.
Here, electron (= e- ) is moving in the circular orbit, which generates electric current I.
"B" is the magnetic field at the point "p".
In the hydrogen's ground state of orbital angular momentum = ℏ, the magnetic moment by electron's orbital motion becomes Bohr magneton
(Fig.14) Magnetic field caused by circular current I
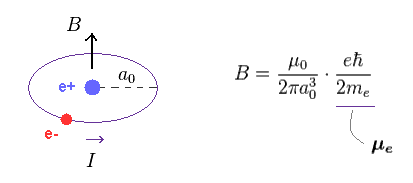
When z = 0 in Fig.13, the magnetic field B at the nucleus (= e+ ) becomes Fig.14.
As I said, this magnitude is inversely proportional to the third power of the distance (= a0 ).
(Fig.15) Bohr magneton = electron magnetic moment.
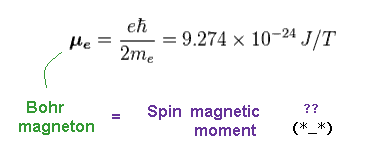
"μe" is Bohr magneton, which is just equal to electron ( spin ) magnetic moment.
(Fig.16) Bohr radius.
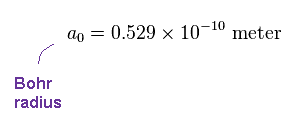
"a0" is Bohr radius (= 0.529 Å ), which is the mean radius of hydrogen ground state.
(Fig.17) Proton spin magnetic moment (= μp ) is much smaller

Proton's magnetic moment (= μp ) is much smaller (= 1/700 ) than electron due to its heavy mass (= mp ).
The important point is that proton's g factor (= 5.58 ) is an experimental (= NOT QED ) parameter assuming ad-hoc Fermi contact interaction equation was right, which is different from Dirac equation. Dirac equation gives only "2"
(Fig.18) Hyperfine magnetic interaction between electron-nuclear spins by simple realistic model without unreal electron spin.
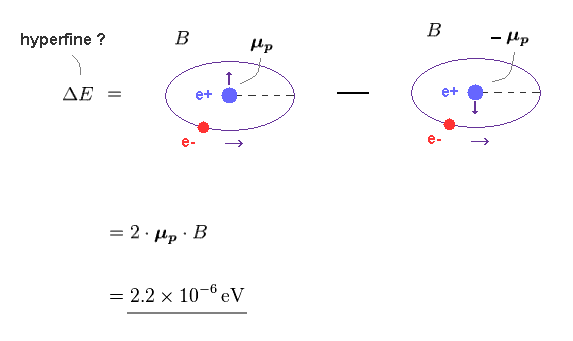
Using Fig.14 - Fig.17, we can know the energy difference between "up" and "down" nuclear spins.
This energy interval becomes 2.2 × 10-6 eV
↑ This realistic hyperfine structure based on electron orbital motion's magnetic field interacting with nuclear spin without electron spin can be derived from this classical magnetic energy equation where distance (between the orbiting electron and nucleus ) is Bohr radius, and two magnetic moments are electron's Bohr magneton and nuclear magnetic moment
(Fig.19) Hyperfine structure.
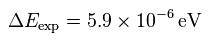
Experimental value of hyperfine structure is 5.9 × 10-6 eV.
So this calculated hyperfine structure value from the realistic electron's orbital motion has almost same order ( ~ 10-6 eV ), which is good agreement, and No violation of energy conservation like the paradoxical quantum mechanical hyperfine structure.
Nuclear magnetic moment is too weak to measure precisely ( this 3rd-paragraph ).
Experimental value of nuclear magnetic moment must be based on various fitting free parameters ( this p.29,31, this p.4-left-2nd-paragraph, this p.3-right-top ).
This p.4-Fig.4 seems to just artificially choose only some frequency change allegedly related to (fictitious) proton spin flip (= there were many frequency shifts irrelevant to proton spin ), which result is unreliable.
And we used the simple atomic model to derive realistic hyperfine magnetic energy, but actually, various factors such as nuclear position's fluctuation can affect the measured values.
(Fig.20) Very weak hyperfine structrue is susceptible to other small effects.
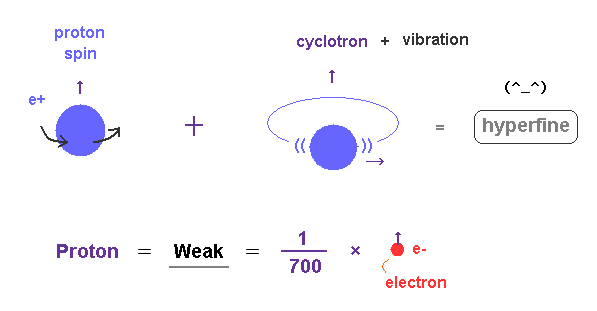
Proton's magnetic moment is extremely small ( about 1/700 × electron magnetic moment ).
So the very weak hyperfine structure is easily affected by other small effects such as nuclear cyclotron and vibration.
First, proton itself is always rotating and moving by the electron's attractive force (= reduced mass ).
It is quite natural that the proton has small energy difference depending on its rotating directions due to "Magnus" effect or something.
(Fig.21) Only when electron is inside proton, it can interact with proton ?
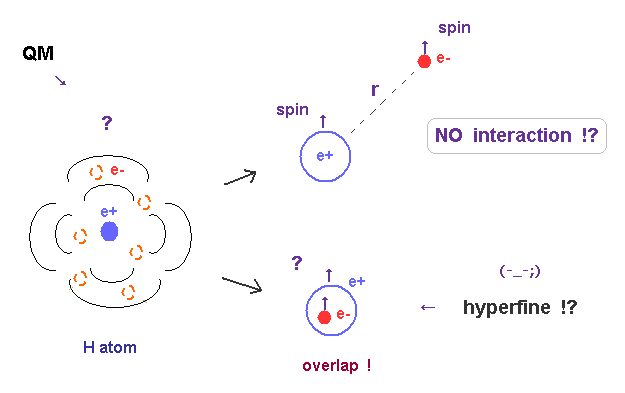
On the other hand, the hyperfine model by quantum mechanics is crazy.
They argue that the electron can interact magnetically with proton, only when it exists inside proton !
(Fig.22) Fermi contact is the leading term.

According to quantum mechanics and this site, Fermi contact interaction (= part of delta function ) is the main factor of 1s hyeperfine, they insist.
(Fig.23) Magnetic field (= B ) created by circular current I.
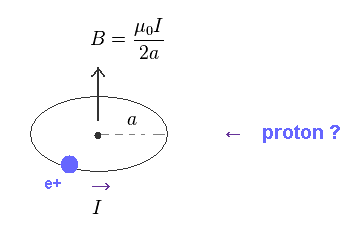
The important point is that there are NO clear reasons for this Fermi contact value (= 8/3π ).
For example, relativistic Dirac equation can only give g-factor = 2 (← NOT proton ) in all fermions.
Surprisingly, "Classical Electrodynamics" ( J.D. Jackson ) says this Fermi contact is based purely on classical electromagnetism ! See this site. So quantum mechanical "spin" is illusion ?
As shown on this site, the magnetic field B produced by circular electric current I is given by Fig.23.
(Fig.24) The total magnetic field included inside proton's sphere ?
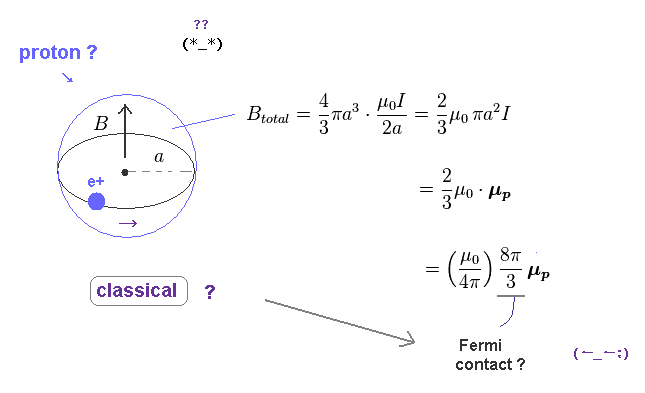
Next, they integrate the magnetic field of Fig.23 over the volume of the sphere (= 4/3πa3 ) to get total magnetic field.
This value of "4/3" related to sphere is the key point.
As a result, this total magnetic field inside the proton's sphere gives Fermi contact
term of Fig.22, they insist.
As you see, this calculation is based purely on classical ( NOT quantum ) mechanics.
(Fig.25) Other magnetic field is cancelled out.
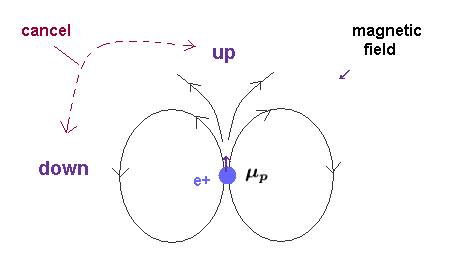
Basically the magnetic field is "closed" system.
So the total magnitudes of "up" and "down" magnetic fields are the same in all space.
If you integrate the magnetic field outside the proton's sphere, you will find the total magnetic field becomes zero.
This means "spin-spin" magnetic interaction ( ex. triplet, singlet ) cannot happen according to this logic.
(Fig.26) Dirac delta function (= δ ).
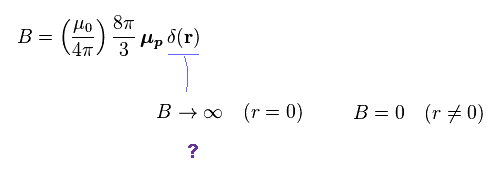
More suprisingly, they concentrate that total magnetic field into the one single point ( r = 0 ) !
So, the magnetic density (= B ) at the origin becomes infinite !
There are No magnetic fields in other places, they insist.
Of course, this situation is completely out of touch with reality.
(Fig.27) Magnetic field B is given by the curl of vector potential A.
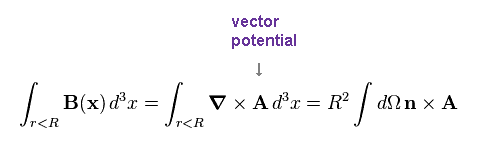
As shown on this site, the magnetic field B is defined by the curl of vector potential A.
This vector potential is defined to be consistent with classical Ampere's ( Biot-Savart ) Law.
They integrate the magnetic field B over the volume of proton's sphere. (← Trick ! )
"R" is the radius of the proton's sphere.
(Fig.28)
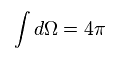
"Ω" is solid angle (= 4π ) in the spherical coordinate.
(Fig.29) Biot-Savart law = "classical" electromagnetism !?
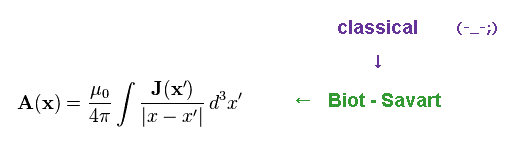
They use the definition of vector potential "A" based on classical electromagnetism.
The relation of Fig.29 gives classical Bio-Savart law. See this site (p.11)
(Fig.30) Total magnetic field.
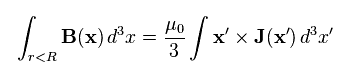
After the long complicated calculation using Fig.27 - Fig.29, they get Fig.30.
The important point is that this method completely depends on the assumption that the proton is a pure sphere.
(Fig.31) Magnetic moment μp of proton.

The magnetic moment μ is given by the area × current.
The integral of Fig.31 expresses the total magnetic moment inside proton.
(Fig.32) Total magnetic field → Fermi contact ?
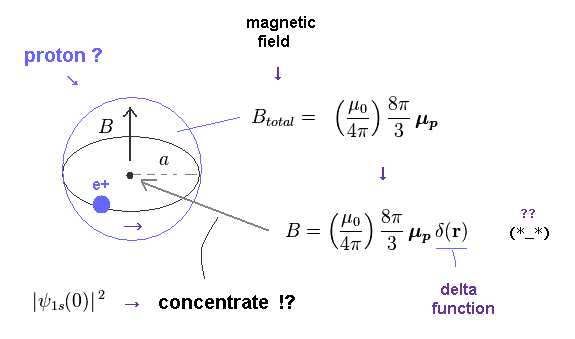
From Fig.30 and Fig.31, we obtain the total magnetic field of Fig.32.
And they concentrate this total B only into the single point ( r = 0 ) using Dirac delta function.
This is also one of artificial tricks.
As a result, they can get Fermi contact term of Fig.22.
(Fig.33) Tiny electron spinning speed is superluminal !?

They derived the Fermi contact term using purely classical mechanics (= circular current + Biot-Savart ).
If classical mechanics dominates even inside proton, the electron spin magnetic moment must be classical, too.
But as shown on this page, the electron spinning speed is much faster than light ( > c ), when its rotating radius is equal to that of a proton.
( Of course, an electron is much smaller, so its speed becomes much faster ! )
(Fig.34) Magnetic field outside proton is cancelled out.

As I said, the integral of the magnetic field over the space (= sphere ) outside the magnetic moment becomes zero.
Because the magnitudes of "up" and "down" magnetic field are just the same.
So the total magnetic field in all space becomes Fig.32.
Of course, this value changes depending on the electric current's shape. ex. circular → elliptic.
This means this obtained value is "model-dependent".
(Fig.35) We can arbitrarily choose the magnetic field area.
In Fig.34, I said the total magnetic field outside proton is cancelled out.
But of course, the magnetic density in each area is NOT zero.
So if we choose other areas as contributing to the total magnetic field of Fig.32 instead of the origin, the probability density of electron's wavefunction (= ψ ) in those areas changes. (= NOT ψ(0) ! )
As a result, the resultant hyperfine structure changes depending on this chosen area.
This means that this method cannot give the definite value as a hyperfine structure, and we can arbitrarily change that value by designating magnetic areas.
(Fig.36) Calculated value is still different from experimental value.
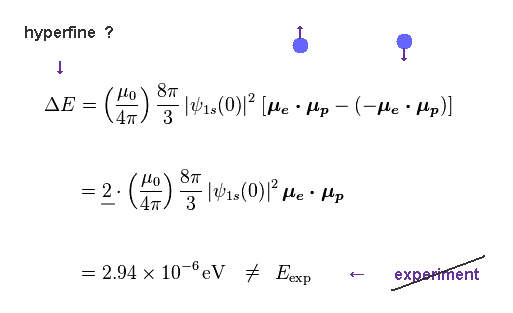
The hyperfine structure expresses the energy difference between "up" and "down" nuclear spins.
As shown in Fig.36, this value based on classical Biot-Savart law cannot give correct hyperfine structure.
So, they had to use other artificial tricks after classical calculation.
(Fig.37) Electron (= S ) and nuclear (= I ) spins.
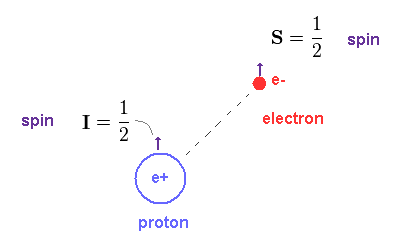
Here "S" is electron spin angular momentum (= 1/2 ), and "I" is nuclear spin (= 1/2 ).
The ratio of magnetic moment to angular momentum (= 1/2 ) is called "quantum" g-factor. See this site.
(Fig.38)
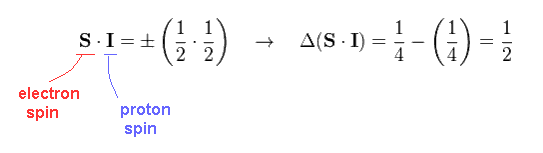
So the product of S mutiplied by I is 1/2 × 1/2 = 1/4.
The different between ±1/4 becomes 1/2, in this case.
(Fig.39)
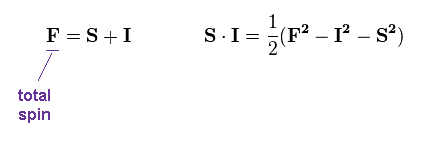
Here they define total spin (= F ).
(Fig.40) ↓ Quantum effect ?
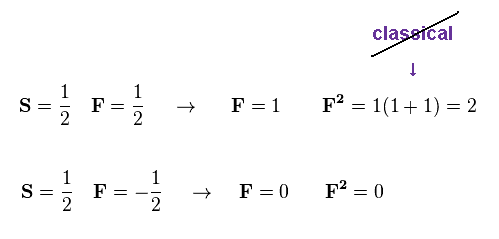
According to the quantum mechanics, the square of F becomes "2", even when F = 1.
(Fig.41)
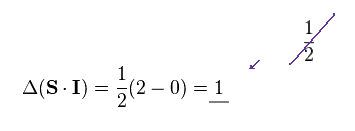
As a result, the difference in ±"SI" becomes twice (= 1 ) the classical value.
( Compare "1" in Fig.41 with "1/2" in Fig.38. This is the last trick. )
(Fig.42) Artificial trick.
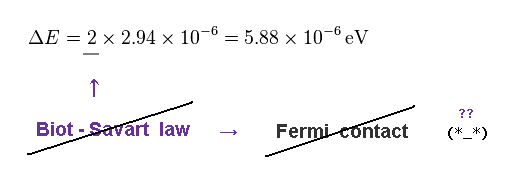
As a result, they can get the value close to experimental hyperfine structrue.
But this method is very ad-hoc, and inconsistent.
As shown in Fig.29, they get the total magnetic field value, depending on purely classical Biot-Savart law.
In spite of this, they completely ignore this definition, and intentionally double the magnetic field using quantum's trick.
Thinking commonsensically, if the last manipulation based on quamtum mechanics is right, calculation using classical electromagnetism itself becomes invalid and cannot be used in the first step.

2014/10/13 updated. Feel free to link to this site.