Top page (correct Bohr model including the two-electron atoms)
Strange "spin" is NOT a real thing
Metallic coordinates inside body.
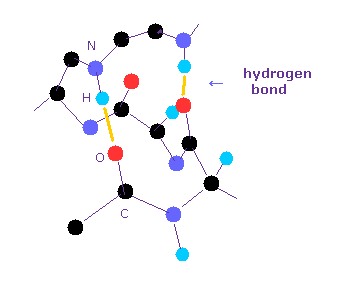
(Fig.1) Hydrognen bonds inside protein.

Hydrogen bonds are so weak that short amino acids cannot usually form hydrogen bonds with each other.
Inside long proteins, hydrophilic parts tend to form hydrogen bonds to be stable surrounded by hydrophobic proteins.
And other hydrophilic residues form hydrogen bonds with water.
In general, the forms of hydrogen bonds are " O -- H-O ", " N -- H-N ", and " O -- H-N ".
Of course, all these hydrogen bonds include hydrogen atom in the middle of them.
Why is hydrogen atom preferable to these bonds ?
(Fig.2) N --- H - N hydrogen bonds.
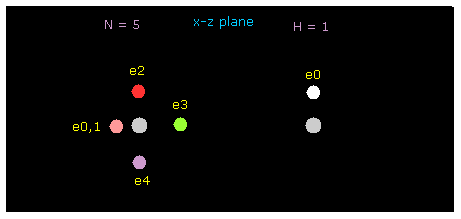
In this section, we use this sample program to investigate hydrogen bonds.
Save this program as "twobin.java" and compile it, neglecting note, "--Xlint: unchecked ---".
Manipulating methods are the same as this page.
(Fig.2') Force = 1000.
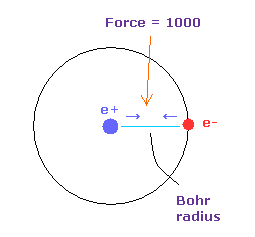
In this page, the force between electron and nucleus in H atom ground state is supposed to be "1000".
So when the distance between electron and +e nucleus is Bohr radius, its force becomes 1000.
For example the force of 1468 is 1.468 times that in H atom ground state.
And new unit of 1 MM = 1.0 × 10-14 meter is used.
(Fig.3) N --- H - N (= nitrogen ) hydrogen bonds
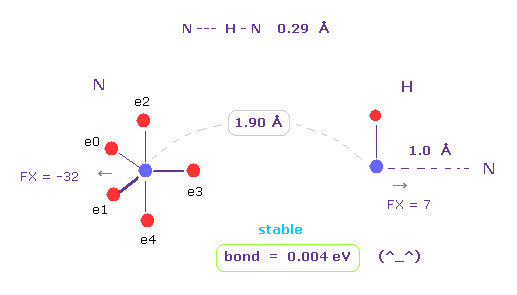
Running the above program, choose "N" (= nitrogen ) and "H" as A and B atoms.
N -- H-N length is about 0.29 - 0.30 Å, so we choose 1.90 Å (= 19000 MM ) as internuclear distance between N and H (= click "internuc" button ).
Because we subtract 1.0 Å N-H covalent bond length from it.
As shown in Fig.3, the binding ( bond ) energy becomes slightly positive (= 0.004 eV ), so this bond is stable.
( Here we don't contract or move hydroen electron, so this binding energy is slightly smaller than the actual value. )
Each nucleus are slightly repulsive to each other, but they are almost zero.
( FX = -32, and FX = 7. )
(Fig.4) If we change "H" atom into "C" atom ? → "unstable".
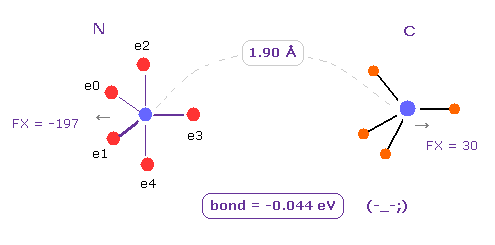
Next we change H atom into carbon (= C ) atom.
Choose "C" and click "Atom B" button.
In this case, binding energy becomes negative (= -0.044 eV ), which means this bond is unstable.
In this program, "A-tV", abd "B-tV" mean total potential energies only inside A or B atoms.
"ABen" ( "ABne" ) mean potential energy among A-electrons (nucleus) and B-nucleus (electrons).
"ABee" ( "ABnn" ) mean potential energy among A-electrons (nucleus) and B-electrons (nucleus).
In N-C bond, repulsive energy among A and B electrons (= ABee ) is much bigger than N-H bond, so it becomes unstable.
(Fig.5) If we change "H" atom into "O" atom ? → "unstable".
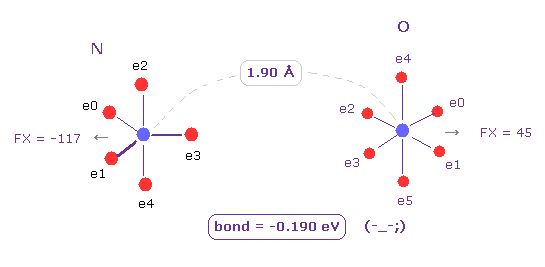
Next we change C atom into oxygen (= O ) atom.
Choose "O" and click "Atom B" button.
Also in this case, binding energy becomes negative (= -0.190 eV ), which means this bond is unstable, too.
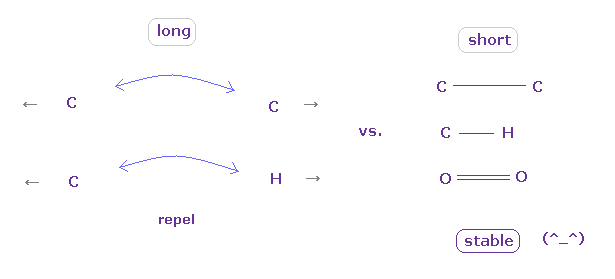
As you see, in the long bond length such as 1.90 Å, repulsive forces among electrons become dominant in N-C and N-O bonds.
This is the main reason why hydrogen atom, which exposes positive nucleus, is chosen as hydrogen bond.
| N - A length | 2.20 Å | 2.10 Å | 2.00 Å | 1.90 Å | 1.80 Å | 1.70 Å | 1.60 Å |
|---|---|---|---|---|---|---|---|
| N - H | -0.006 | -0.004 | -0.001 | +0.004 | +0.013 | +0.029 | +0.055 |
| N - C | -0.133 | -0.117 | -0.09 | -0.044 | +0.031 | +0.154 | +0.355 |
| N - O | -0.197 | -0.199 | -0.197 | -0.190 | -0.173 | -0.138 | -0.069 |
As shown in Table 1, other atoms such as carbon and oxygen have stronger repulsive forces of their valence electrons. So they cannot form stable hydrogen-like bonds with N.
On the other hand, hydrogen with only one electron can form stable hydrogen bonds with N atom even in such a long bond length (= 1.90 Å ).
( Carbon is often surrounded by 4 atoms, so N cannot come close to this carbon. )
Basically, as bond length becomes shorter, and close to its actual covalent bond length, binding energy becomes bigger.
( Covalent bond length, N-C is 1.47 Å, and N-O is 1.40 Å ).
So to form stable covalent bonds, each atom need to come closer to each other than some threshold.
(Fig.6) H -- O-H hydrogen bond.
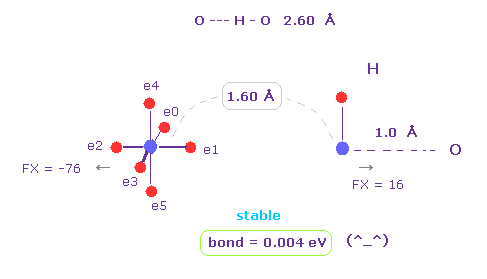
H -- O-H hydrogen bond length is about 2.60 - 2.70 Å.
We choose "O" and "H" as A and B atoms, and make internuclear distance "1.60 Å" (= 16000 MM ).
And rotate "O" atom by 45 degree on x-y plane ( input "45", and click "x-y ang" button. )
Also in this case, binding energy becomes positive (= 0.004 eV ), and O-H bond becomes stable.
And repulsive force between nuclei is almost zero ( FX = -76, FX = 16 ).
( These are almost zero, but slightly "repulsive", so O-H or N-H bond length doesn't become shorter. )
(Fig.7) O - C bond is "unstable" in the long bond length.
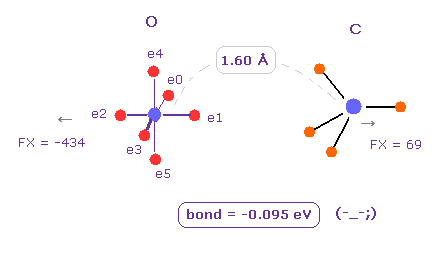
Next we change H atom into C atom. ( Choose "C", and click "Atom B" button. )
In this case, binding energy becomes negative (= -0.095 eV ).
So as I said above, repulsive forces among valence electrons are stronger in such a long O-C bond length.
( Of course, oxygen cannot come close to carbon, which is surrounded by 4 other atoms. )
(Fig.8) O - O bond is "unstable", too.
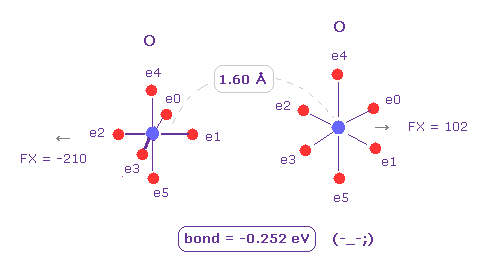
Next we choose "O" (= oxygen ) as Atom B ( choose "O" and click "Atom B" button ).
Also in this case, binding energy becomes negative (= -0.252 eV ), which means unstable.
So in this long bond length, repulsive forces among electrons become dominant in O-C and O-O bonds.
| N - A length | 1.90 Å | 1.80 Å | 1.70 Å | 1.60 Å | 1.50 Å | 1.40 Å | 1.30 Å |
|---|---|---|---|---|---|---|---|
| O - H | -0.011 | -0.009 | -0.004 | +0.004 | +0.022 | +0.054 | +0.113 |
| O - C | -0.205 | -0.190 | -0.158 | -0.095 | +0.020 | +0.232 | +0.612 |
| O - O | -0.261 | -0.266 | -0.265 | -0.252 | -0.215 | -0.122 | +0.092 |
As shown in Table 2, O-H bond becomes stable even in the long bond legnth (= 1.60 Å) due to its exposed nucleus.
In other atoms such as C and O, repulsive force aomg valence electrons are dominant.
Also in this case, as bond length becomes shorter, its bond become covalent-like and stable.
(Fig.9) When they choose steric hindrance or covalent bonds.
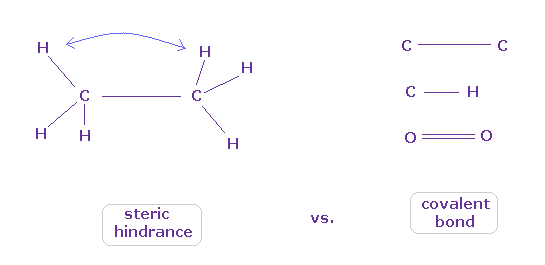
You often see the explanations such as " six hydrogen atoms of ethane tend to avoid each other." or "protein structures are very limited due to their steric hindrance".
So this means each atom "always" avoids other atoms ?
On the other hand, various atoms except for noble gases can form stable covalent bonds.
Though each atom "avoids" each other, why they can form stable and tight covalent bonds ??
These differences depend on their bond length, as I said in above section.
(Fig.10) C-C = 1.5400 Å is an equilibrium length.
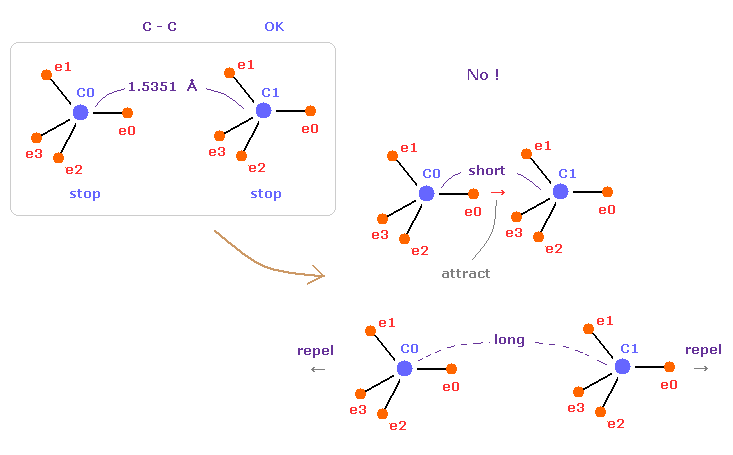
In this page, we show C-C bond length (= 1.5351 Å ) is indispensable for the stability of both C nuclei.
If C-C bond length is shorter than 1.5351 Å, attractive force between e0 and C1 becomes too stronger, and it's unstable (= binding energy becomes bigger. ).
And if C-C bond length is longer than this, repulsive force between two C nuclei becomes dominant, and it's unstable (= binding energy becomes negative ).
This is the true mechanism of C-C bond length.
(Fig.11) When C-C bond becomes stable ?
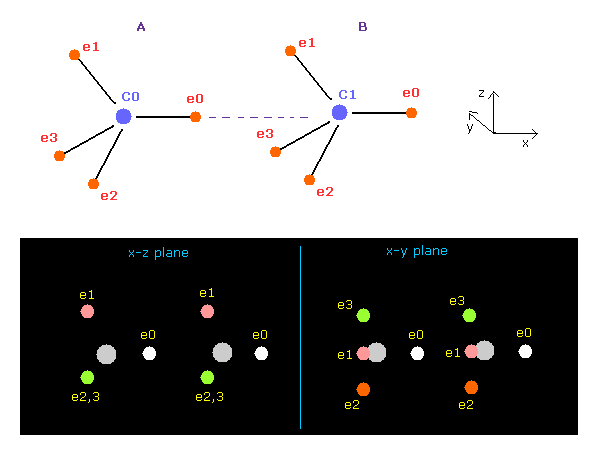
Using above program, we compute forces acting on each C nucleus.
Choose "C" and "C" as A and B atoms.
| internuc (MM) | A nuc force | B nuc force | Difference |
|---|---|---|---|
| C-C 15351 | FX = -340 | FX = -341 | = -1 |
As shown in Table 3, when the internuclear distance of C-C is the experimental value (= 1.5351 Å ), the forces x component (FX) acting on A and B nuclei becomes -340 and -341, which keeps stable internuclear distance.
| C-C (MM) | A nuc FX | B nuc FX | Difference |
|---|---|---|---|
| 12000 | -856 | -1703 | -847 |
| 13000 | -633 | -1013 | -380 |
| 14000 | -479 | -627 | -148 |
| 15000 | -370 | -399 | -29 |
| 15351 | -340 | -341 | -1 ← |
| 16000 | -292 | -258 | +34 |
| 17000 | -234 | -168 | +66 |
| 18000 | -191 | -109 | +82 |
| 19000 | -158 | -69 | +89 |
If you enter the value of C-C internuclear distance (MM) into the designated textbox and click "internuc" button, you can change bond length freely.
Table 4 shows the difference between force component FX acting on A and B nuclei.
When the internuclear distance becomes shorter, this difference becomes negative.
( This means each C nucleus and valence electrons are too much attracted, and covalent bond becomes unstable. )
(Fig.12) C-C bond length is experimental value = 1.5351 Å
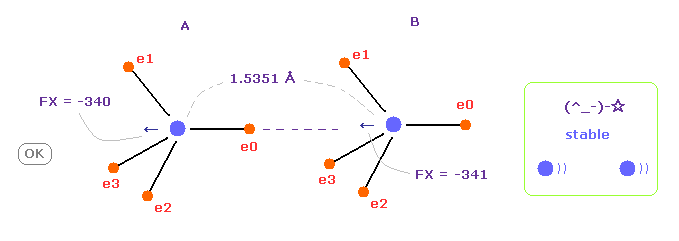
When C-C bond length is experimental value, forces acting on A and B nuclei are almost same.
( FX = -340 and -341 ).
This means C-C bond length is in equilibrium and stable.
And this result shows Coulomb and de Broglie relations are effective also in actual C-C bond.
(Fig.13) C-C bond length is shorter = 1.4000 Å
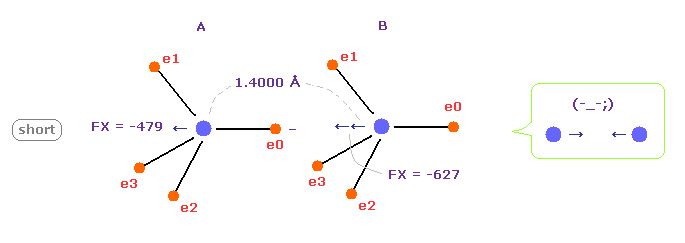
When C-C bond length becomes shorter (= 1.4000 Å ) than experimental value, B nucleus is attracted too strongly to electron e0 of A atom.
This means C-C bond length becomes unstable and tries to be much shorter in this case.
(Fig.14) C-C bond length is "longer" = 1.7000 Å → they "repel" each other.
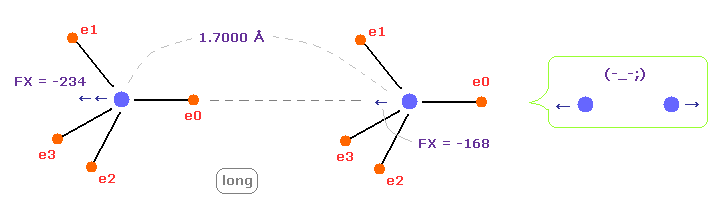
When C-C bond length becomes longer (= 1.7000 Å ) than experimental value, repulsive force between two nuclei ( electrons ) becomes stronger.
This case corresponds to above section of hydrogen bonds.
Generally, bond length becomes longer. binding energy tends to be negative, as I said avove.
This means C-C bond length becomes unstable also in this case.
As a result, when C-C bond length is experimental value, its distance is stable.
(Fig.15) Repeat upper and lower states.
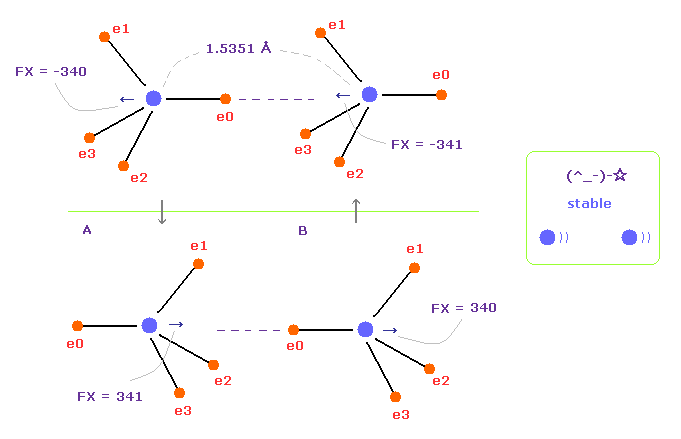
Overall forces of Fig.12 is toward minus x direction.
But valence electrons are moving around each nucleus, so upper and lower states of Fig.15 repeat.
Summing upper and lower states of Fig.15, total force acting on nuclei becomes almost zero.
(Fig.16) "Long" or "short" bond length determines their property.
In conclusion, to form stable covalent bonds, two atoms need to come close to each other than some threshold length.
When it is longer than the threshold length, repulsive forces among electrons or nuclei become dominant and causes steric hindrance.
In usual proteins, almost all distances between two atoms are longer than covalent bond length, so they tend to cause steric hindrance.
(Fig.17) Infinite bare charge and mass + "wrong" math = QED.

It is said quantum electrodynamics (QED) achieves full agreement between quantum mechanics and special relativity, and is one of most successful theories in the physical history.
But as shown in this page, QED neglects infinity to get very tiny value, and completely depends on virtual photons, which disobey special relativity.
Furthermore, QED completely depends on "wrong" math.
In this page, we confirm QED uses wrong math again.
If g-factor of QED is wrong, its computed g-factor value is also used in a part of Lamb shift, so QED Lamb shift is wrong, too.
(Eq.1) "Artificial" trick in QED.

Eq.1 is the fundamental mistake in calculation in QED g factor (= anomalous magnetic moment )
In Eq.1 upper, the integral of odd function "k" becomes zero.
( The interval of integration is from -∞ to +∞ to satisfy Lorentz invariant. )
After the change of variables ( k = l - β ), The part of " l " becomes zero due to odd function.
As a result, only "-β" is left, which includes the information of g-factor.
This math is indispensable for getting g-factor in QED.
Of course, the math of Eq.1 is wrong, because the "change of variable" cannot change the result itself !
(Eq.2) Right math.
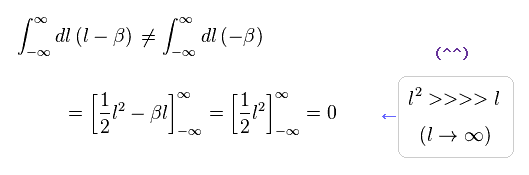
If we use a right mathematical method, the part of "-β" becomes zero, too.
Because after the integral, " l2 " term diverges much faster than " βl " term.
As a result, only " l2 " term is left, and becomes zero.
( It is quite natural that "change of variable" is just a "method", and cannot change the result itself ! )
So QED mathematical method of Eq.1 violates basic math.
(Eq.3) Application of "wrong" math in actual QED calculation.
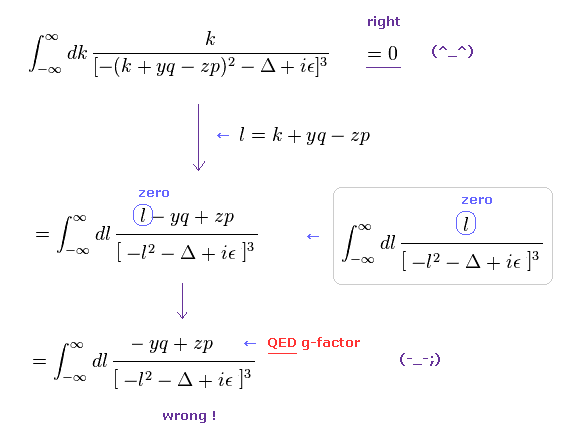
As shown in this page, we apply wrong math of Eq.1, like Eq.3.
The equation of the first line is zero in the "right" math.
( Other values (= y, q, z, p, Δ ) excluding "k" are finite. )
But if you use this "right" math, you cannot get QED g-factor.
In QED g-factor, you must use "change of variable" ( k + yq - zp → l ), and use wrong math cleverly for ordinary people NOT to notice its mistake so easily.
In the second line of Eq.3, the denominator is an even function of l2, and "l" in numerator is an odd function, so they make only "l" in the numerator zero, and treat the remaining "- yq + zp" as a part of g-factor.
( Of course, this math is wrong. )
(Eq.4) Integration by parts.
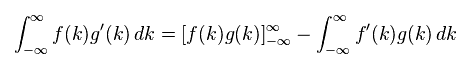
Here we prove Eq.3 is zero, using the integration by parts of Eq.4.
( Or you can prove Eq.3 is zero, if you use formula of rational function directly. )
(Eq.5)
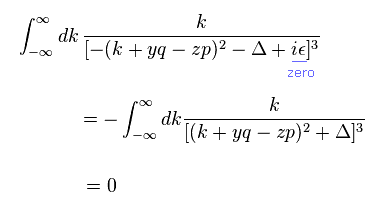
Here, infinitesimal value of ε is zero.
Using integration by parts of Eq.4 in Eq.5,
(Eq.6)
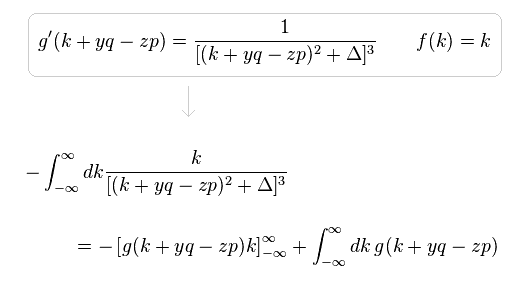
In Eq.6, when "k" is close to ±∞, the difference between "k+yq-zp" and "k" is gone, as follows,
(Eq.7)
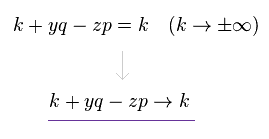
So we can change variables like Eq.7 in g(k+yq-zp), keeping the same calculating results.
As a result, Eq.6 is equal to
(Eq.8)
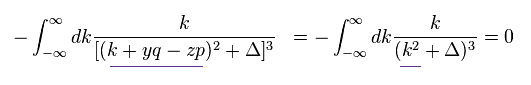
The denominator of Eq.8 is an even function of "k".
The numerator of Eq.8 is an odd function of "k".
So Eq.8 is zero, which means Eq.3 (= Eq.5 ) proves to be zero, too.
This means QED calculation in Eq.3 is wrong, because, it doesn't become zero to leave g-factor value "artificially".
Eq.5 can be expressed as Eq.9.
(Eq.9)
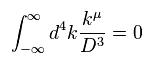
where
(Eq.10)
In Eq.10, x, y, z satisfies x + y + z = 1, and each value is from 0 to 1.
( See also this page (Eq.74). )
(Eq.11) Numerator of g-factor equation.
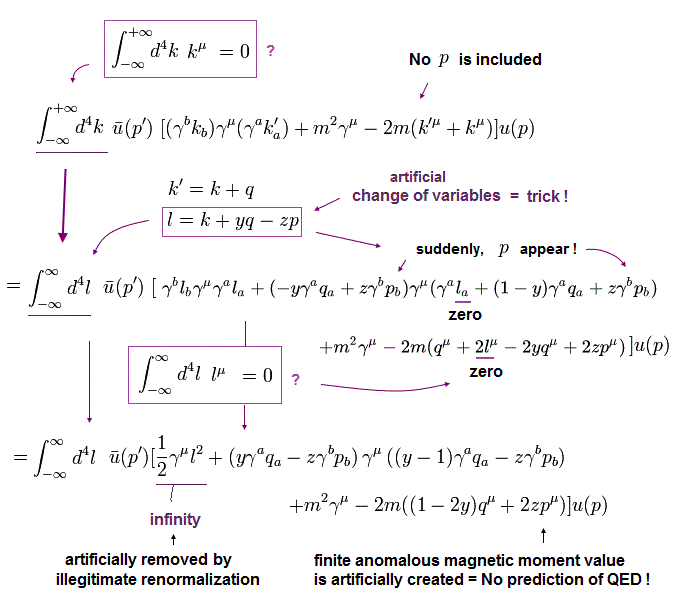
As shown in this page (Eq.3), we must get the second line of Eq.11 as a numerator to obtain correct g-factor value.
But of course, this math is wrong.
If you adopt right math of Eq.5, this result becomes completely different.
Here we prove it.
In Eq.11, "q" is photon, "p" is electron, and "k" is in the electron's propagator.
And as shown in this page ( Fig.18 and Eq.36 ), Eq.12 is satisfied.
(Eq.13)
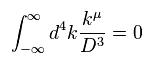
Using Eq.10, Eq.12 and Eq.13 (= Eq.6 ), we can change Eq.11 into Eq.14.
(Eq.14) "Right" math.

In the first line of Eq.14, the integral of odd function of "k" becomes zero, as I explained in Eq.5 and Eq.6.
Furthermore if we use Eq.13 and Eq.15, almost all values becomes zero except for infinity (= l2 part ).
(Eq.15)
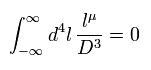
Even if you change ( k + yq - zp ) of the denominator in Eq.5 into just "k", this result becomes zero, too.
Because infinity absorbs finite change.
So if Eq.13 is satisfied, Eq.15 is also satisfied. ( See Eq.8. )
(Eq.16) "Right" math = g-factor is "gone" somewhere.

As a result, if we use "right" math of Eq.3 upper, we cannot get correct g-factor value at all.
Because it does NOT include "p" (= electron entering vertex ) at all, as shown in the last line of Eq.16.
As a result, QED g-factor, which is said to be one of successful precision tests, is just a mistake in calculation.
(Eq.17)
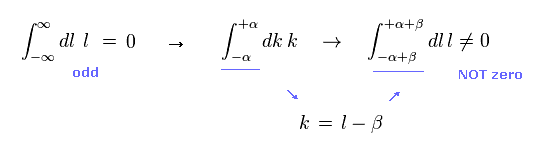
QED g-factor uses only Eq.15, and consider right math of Eq.13 is wrong.
But this idea is self-contradictory.
Because, to use Eq.15, we have to neglect finite change when we change variables in the integral.
Though they neglect finite change to get Eq.15, they don't neglect it in Eq.13.
This is clearly one of self-contradictions and "artificial" tricks.
In addition to this trick, they have to make virtual photon "zero" to get g-factor.
But in this case, g-factor ( and Lamb shift ) can be arbitrary values, and cannot be determined as a single value.
( See also this page ( Fig.11 - Eq.18 ). )
(Fig.18) Why they "blindly" reject new inportant results ?
The recent interesting experiments showed that various phenomena disobey QED.
(Pohl, R. et. al. Nature 466, 213-216 (2010), J. K. Webb, et.al. Phys. Rev. Lett. 107, 191101 (2011), C. T. Chantler, et.al. Phys. Rev. Lett. 109, 153001 (2012) ).
I imagine it was very hard task to publish experimental results, which are inconsistent with the conventional quantum theory and relativity.
So they were courageous and respectable.
First, as shown in this page, special relativity includes fatal paradoxes.
So it is quite natural that more experimental results, which are inconsistent with conventional QED, should appear.
Various journals should abandon "preconceived" ideas and try to judge the results more fairly, I think
We should not be misled by preconceived notions that special relativity is absolutely right, and should not give up various true experimental results such as faster-than-light neutrino so easily.

2013/6/6 updated. Feel free to link to this site.