Home page
Quantum computer is dead.
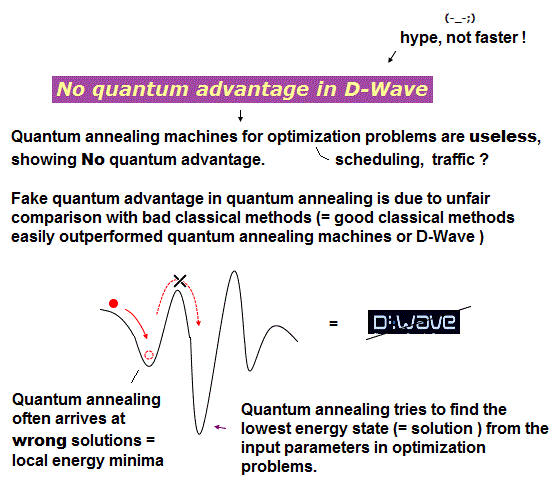
(Fig.1) Quantum annealing or D-Wave for optimization problems is useless, showing No quantum advantage.
Quantum annealing machines or quantum adiabatic computers are said to solve optimization problems finding the lowest energy states ( this p.2-4 ) encoding the fastest route, efficient scheduling, logistics, traffic flow under given conditions.
But these quantum annealing machines represented by D-Wave are Not real quantum computers, so No quantum advantage nor speed-up in this fake quantum annealing computer ( this 6th-paragraph, this p.2-right-1st-paragraph, this p.4,p.16 ).
This 1st-paragraph says
"But despite D-Wave’s confidence, scientists and academics say the company has never proved its advantages over normal computers. And, more damningly, that using the company's current methodologies, it never will."
This p.2-left-last-paragraph (11/7/2024) says
"Unfortunately, there is No clear evidence
that quantum annealers would provide quantum advantage" ← No quantum advantage.
This 6th-last-paragraph (11/1/2024) says
"So far, though, most quantum optimization algorithms offer less than exponential speed-ups. Because quantum hardware operates much slower than current transistor-based electronics (= classical computers are faster )"
This paper (2024)
p.10-2nd-last-paragraph says "quantum annealers are too small and too prone to errors"
p.12-conclusion-1st-paragraph says "we have not yet demonstrated
a quantum advantage"
Many overhyped claims that these annealing machines might be faster than ordinary classical computers are based on unfair comparison with bad classical methods (= good classical computer's methods easily outperformed quantum annealing or D-Wave ).
(Fig.1') Good classical computer's methods (= Selby ) outperformed quantum annealing or D-Wave.
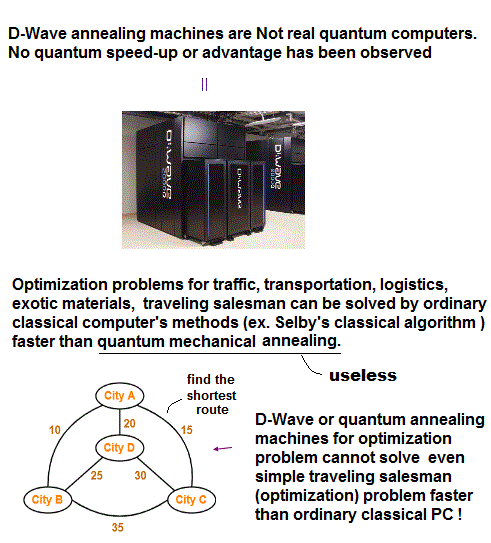
It is known that these quantum annealing machines are slower and more error-prone than ordinary classical computers using best classical calculation methods such as (classical) Selby's algorithm ( this 6th-paragraph, this 2nd-paragraph, this p.6-left-c ).
This 3rd-pagagraph says
"on every instance tested so far, Selby's (classical) annealing algorithm outperforms the D-wave machine,... they strategically included an unfair benchmark so that the news media could take the 100M speedup figure to fuel the hype machine"
This 15th, 19th paragraphs say
"So besides (classical) simulated annealing, there are two more classical algorithms that are actors in this story. One of them is quantum Monte Carlo, which is actually a classical optimization method (= simulated annealing and Monte Carlo are bad slower classical computer's methods )"
"What the Google paper finds is that Selby's algorithm, which runs on a classical computer, totally outperforms the D-Wave machine on all the instances they tested"
↑ The faster classical computer's method called Selby outperformed D-Wave annealing machines.
This 2nd-last-paragraph says
"The VW research team also notes that their primary goal is.. not to prove supremacy over every existing classical clustering algorithm." ← Because quantum annealing is slower than the good classical computer's method.
↑ So all the overhyped ( fake ) quantum advantage claims in quantum annealing (= QA ) optimization problems is due to unfair comparison with slower bad classical methods such as simulated annealing (= SA ) and Monte Carlo (= MC ), as shown in this p.1-right-1st-paragraph, this p.5-left benchmark against simulated annealing, this p.47-X (= all of which did Not compare quantum annealing with faster classical methods such as Selby ).
Classical computer's best faster algorithm such as Selby can easily outperformed quantum annealing machines (= classical Selby gave more accurate results than the error-prone D-Wave (= DW ), this p.16-Table.2, p.15-lower ).
In some tasks, even against slow classical simulated annealing, quantum annealing could not show quantum advantage ( this p.1-abstract-lower ).
As a result, contrary to many (unfounded) hypes, (fake) quantum computers or quantum annealing are slower and showing No quantum advantage over ordinary classical computers ( this p.1-last ).
Actually, despite extremely longtime research and hypes, still Nobody and No companies use these overhyped D-Wave annealing machines for practical optimization problems (= Only a tiny number of companies use D-Wave only for fruitless researches or spreading hypes to get investment money or research funds ).
This p.2-4th-paragraph (9/9/2024) says
"the current implementations of quantum annealing in optimisation are limited in size and Not yet upscaled
to real-world situations" ← Quantum annealers or D-Wave are still useless.
This 8th-paragraph (5/23/2023) says
"but to date, No quantum computer has outperformed a classical supercomputer in practical tasks"
Also in one of optimization problems called travelling salesman problem finding shortest route, quantum annealing machines showed No advantage over classical computers ( this p.1-abstract, this abstract ).
This 5th-last-paragraph says
"In fact, it hasn't been proved yet that quantum annealing gives an advantage over classical optimization algorithms"
(Fig.2) Classical electric current difference induced by applied magnetic field generates D-Wave's flux qubit-0 and 1 states.
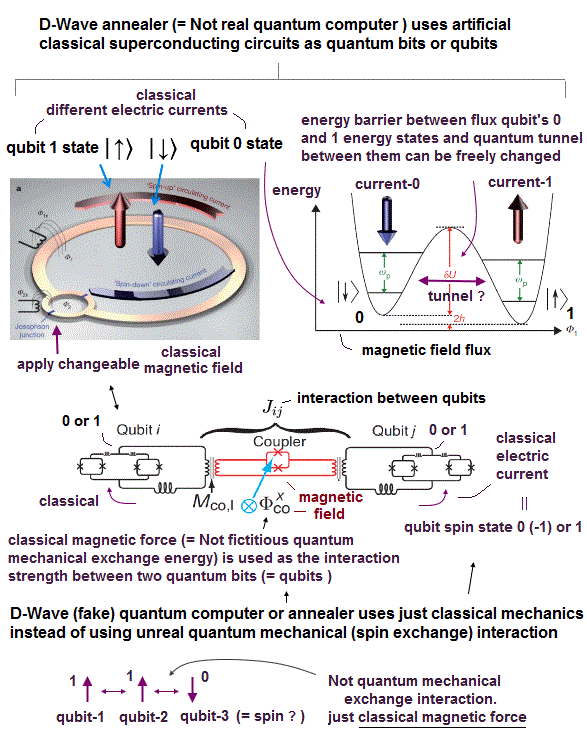
D-Wave annealing machines use the direction of classical electric current flowing through the superconducting circuit as their ( flux ) qubit state 0 or 1. No quantum mechanics is used.
Electron's current tends to be quantized due to the (classical) electron's ( an integer times ) de Broglie wavelength in D-Wave's superconducting flux qubit or circuit that can be manipulated by external magnetic field ( this p.6-7 ).
↑ By adjusting applied magnetic field (= flux ) in qubits (= classical superconducting circuits ) and couplers connecting qubits, D-Wave can optimize the final lowest-energy stable solution.
Quantum tunneling is a realistic classical phenomena (= electric current over only very short distance ) irrelevant to unrealistic quantum mechanical negative kinetic energy
(Fig.3) One of bad time-consuming classical methods called path integral Monte-Carlo (= PIMC ) ↓
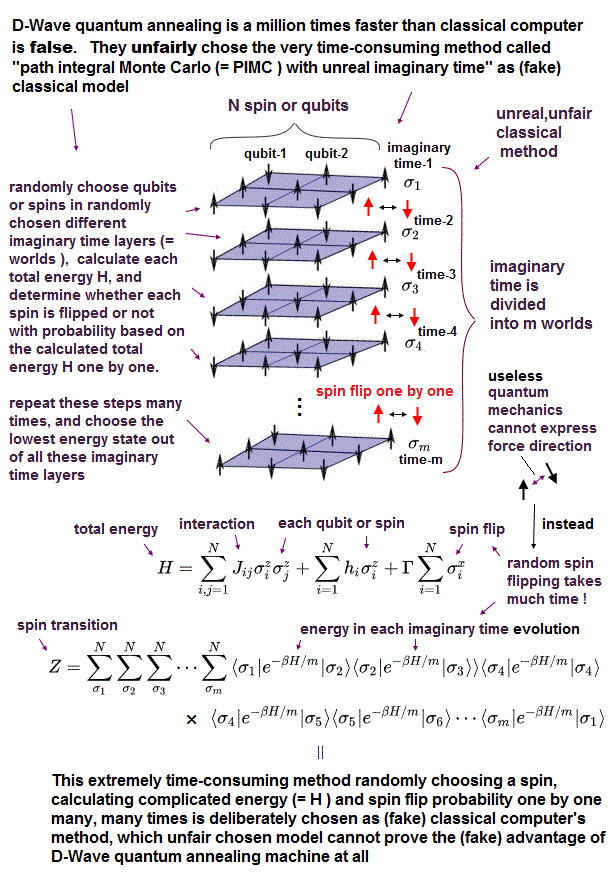
The (fake) quantum advantage of quantum annealing or D-Wave is caused by comparison with the artificially-chosen bad slow classical computer's methods such as simulated annealing and Monte-Carlo.
One of those bad classical methods is path integral Monte Calro (= PIMC ) method or quantum Monte Carlo (= QMC, this Fig.1B ) using the unreal imaginary time, which means PIMC can Not represent the realistic classical calculation method at all.
In this unrealistic very time-consuming classical method called path integral Monte Carlo, they first divide the process of annealing into many fictitious imaginary time periods (= σ1, σ2, σ2 .. σm, this p.2 ).
And then, they randomly chose an arbitrary qubit representing "spin direction" included in random imaginary times one by one, calculated the total energy (=H ) before and after the qubit (or spin ) flip ( 0 ↔ 1, this p.2 ), and decided whether this chosen qubit is flipped or not based on the calculated imaginary-time probabilities (= function of total energy, this p.30-40 ), until the system may reach the lowest energy state ( this p.20, this p.8, this p.9, this p.9 ).
↑ This impractical Monte Carlo classical method takes extremely much time, because it must randomly calculate each qubit's energy or flipping probability one by one without knowing the real forces by which all qubits naturally decide whether they flip or not simultaneously to lower the total energy.
Whether quantum or classical, all things and particles in the nature are gradually evolving into the lowest energy state by interacting and exerting real forces on each other simultaneously, which real classical process in the nature is completely different from these impractical extremely time-consuming artificial classical methods such as path integral Monte Carlo and simulated annealing unfairly chosen for comparison with the quantum annealing.
(Fig.4) Setting the right prime numbers (= 5 and 3 ) as the lowest-energy qubit state for factoring 15 = 5 × 3 using (impractical) quantum annealing.
Quantum annealing machines for optimization problems are said to be able to factor numbers.
They encode solutions of factorization into the lowest energy state (= expressed as binary qubit states ) in D-Wave annealing machines.
The problem is quantum annealing or D-Wave often give wrong answers stuck in one of local energy minima instead of the lowest energy state (= right answers, this p.3 ).
Even in factoring the simplest 15 = 3 × 5, D-Wave annealing machines are known to often give wrong answers ( this p.55, this p.7-Figure 1, this p.34 ).
So it is impossible to use the error-prone quantum annealing or D-Wave for practical factoring or some calculations. Only hypes remain.
Feel free to link to this site.
