Top page (correct Bohr model including the two-electron atoms).
Electron spin is an illusion !
Our new Bohr model has succeeded in calculating the Helium ionization energy more correctly than the quantum mechanical variational methods as shown in the Top page.
In this new successful Bohr model, the two electrons of the helium atom (He) are moving on the orbits of just one de Broglie's wavelength which are perpendicular to each other.
This model can explain the phenomena of Pauli exclusion principle correctly, because there is no space for the third electron to enter this new two-electron Bohr atom.
Surprisingly, this new atomic structure of the Bohr model can be applied to other atoms (ions ), Lithium, Carbon, too.
(For example, see Bohr's Lithium page.)
Methane is a chemical compound with the chemical formula CH4.
Methane is a colorless, odorless, and nonpolar gas due to its "tetrahedral" structure. (Bond angle is 109.5 degrees.)
The ordinary quantum chemstry says that
for the C-H bond of methane, the sp3 hybrid orbital must be formed instead of 2s and 2p orbitals.
But the quantum mechanics doesn't have the power to say more concrete and detailed structure about this chemical bond.
Because the quantum mechanics (chemistry) can not express the "real" physical images.
(It only shows the "mathematical" model). (See also this page)
Bohr model was able to express the hydrogen atom correctly as well as the Schroedinger equation.
(And Bohr-Sommerfeld model could express the relativistic effects of the hydrogen atom correctly as well as the Dirac equation. See also this page.)
Furthermore, we can compute the approximate orbits of carbon using the Bohr- model based methods.
In this carbon model, four valence electrons of carbon atom are arranged "tetrahedrally" around the nucleus.
(See also this page.)
So, here we try to explain the methane molecule (CH4) by this new Bohr model, and seek "real" electron's motions of CH4.
In the methane molecule, 435 kJ/mol is required to break a single C-H bond.
But breaking all four C-H bonds for a mole requires 1663 kJ ( = 17.235 eV ).
Thus the average bond energy is 1663/4 = 416 kJ/mol, which is not equal to 435 kJ/mol.
So the ground state energy of methane (4 carbon's valence electrons + 4 hydrogen atoms) becomes -148.024 -54.416 -17.235 = 219.675 eV.
The neutral carbon has six electrons (2 × 1S electrons + 4× valence electrons), in which two 1S electrons are very close to the nucleus.
So approximately we suppose these four electrons are moving around one +4e central nucleus (+6e-2e = +4e).
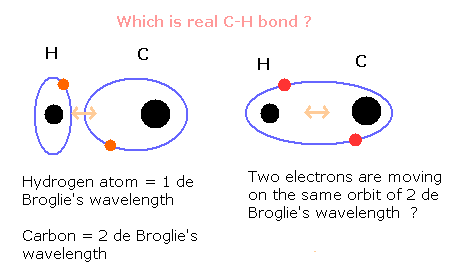
The important point is the relation between the hydrogen's and the carbon's electrons.
Originally, the hydrogen atom has one orbit of 1 de Broglie's wavelength.
On the other hand, the outer shell electrons of carbon moves the orbit of 2 de Broglie's wavelength.
(This fact is confirmed by the energy calculation of carbon ion (C3+). See Bohr's Carbon.)
When C-H bond is formed, how do these two orbitals change?
The hydrogen atom can keep the orbital of 1 de Broglie's wavelength ?
Or two electrons of the hydrogen and the carbon's outer shell electron form one "hybrid" orbitals of 2 de Broglie's wavelength ?
Fig. 1. Which is a "real" C-H bond of methane (CH4) ?

To answer this question, we investigate the motions of methane's electrons by computing the Coulomb forces among the particles at short time intervals using the next sample JAVA program.
Sample JAVA program (CH4)
Fig. 2. Estimated methane (CH4) "real" structure
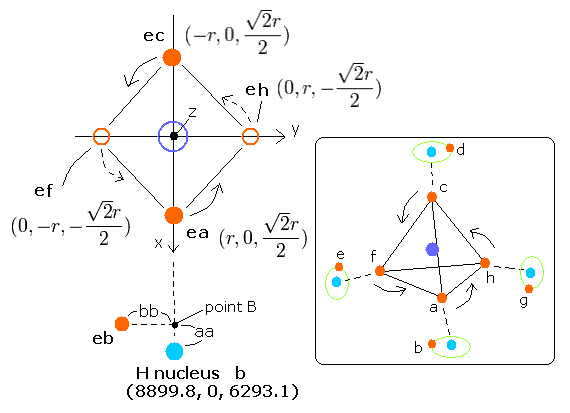
In this program, the carbon nucleus (it is supposed to be +4e =+6e-2e) is at the origin, and the four hydrogen nuclei are arranged "tetrahedrally".
The average bond length of C-H bond is 1.09 × 10-10 meter (=10900 MM).
For calculation, here we use the new units as follows,
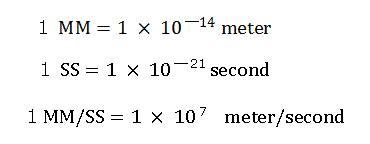
We fix hydrogen nuclei as follows (in MM);
Hydrogen b nucleus --- (hbx, hby, hbz) = (8899.8, 0, 6293.1)
Hydrogen d nucleus --- (hdx, hdy, hdz) = (-8899.8, 0, 6293.1)
Hydrogen e nucleus --- (hex, hey, hez) = (0, -8899.8, -6293.1)
Hydrogen g nucleus --- (hgx, hgy, hgz) = (0, 8899.8, -6293.1)
In this program, we first input the initial x-coordinate r (in MM) of electron a (ea).
And about the electron b (eb) of hydrogen atom, we input the initial coordinates aa and bb (in MM);
aa = distance between the hydrogen b nucleus and the point B (=projection of electron b's coordinate onto the line connecting the origin (=carbon nucleus) and hydrogen b nucleus.
(When the aa is minus, this point B and the origin are on the opposite sides of hydrogen b nucleus from each other.)
bb = distance between this point B and electron b. (When bb is positive, y coordinate of electron b becomes minus.)
From the inputted values, the four carbon's outer shell electrons (ea,ec,ef,eh) and four hydrogen electrons (eb, ed, ee, eg) are arranged tetrahedrally like Fig. 2.
When the electron a (ea) has moved its orbit of 1.0, 1.9, and 2.0 de Broglie's wavelength, and the electron b has moved its 1 de Broglie's wavelength orbit, this program outputs the following values on the screen:
coordinate of each electron,
initial and last distance between nucleus of carbon (or hydrogen) and electron a (or b),
longest and shortest distances between nucleus and electron a in the orbit.
Probably, the directions of the initial velocity vectors are changing slowly due to the precession.
But it is very complicated, so we fix the condition of the initial velocity vectors as follws,
Ratio of each component of the velocity vector of electron a is ( 0, 8, -1 )
Ratio of each component of the velocity vector of electron b is ( 0, 0, vb )
When the initial x coordinate (r) of electron a is 5500 MM (= 0.5500 × 10-10 meter), and
initial aa and bb are -700 and 3750, respectively,
all electrons can be back to the nealy initial condition when the number of de Broglie's waves contained in the ea's orbits (wa) becomes 1.9 ˜ 2.0 (with a little precession).
Initial distance between electron a and nucleus is 6736 MM, and its last distance is 6535 MM.
Initial y coordinate of electron a is 0 MM, and its last y coordinate is 422 MM ˜ 2328 MM.
The longest distance between the nucleus and electron in the orbit is 7169 MM (= nealy initial distance), and its shortest one is 4805 MM .
In case of electron b (eb), when the wa becomes 2.0, the number of de Broglie's waves contained in eb's orbit becomes almost 1.0.
Initial distance between electron b and hydrogen b nucleus is 3814 MM, and its last distance is 3588 MM.
Initial y coordinate of electron b is -3750 MM, and its last y coordinate is -2286 MM ˜ -1269 MM.
If we suppose the electron a and electron b are moving on almost same orbit of 2 de Brogli's wavelength and execute the program , the electron b can not reach the carbon's nucleus, because the carbon's positive nucleus desn't have the attracting power enough to make electron b orbit around carbon's nucleus.
(And in this case, total energies of electron a and b must be the same.)
This result shows that the hydrogen atom keeps the orbital of 1 de Broglie's wavelength which is different from carbon's orbital in Fig. 1.
See also this page (Virial theorem of CH4).
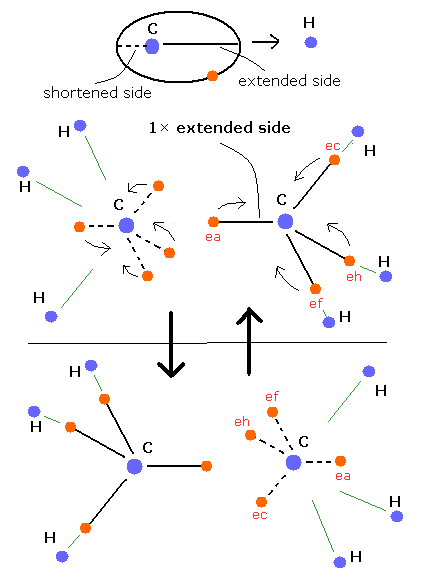
As shown in the upper methane section, when there are other atoms' positive nuclei, the carbon's electron orbit is extended by the attractive Coulomb force on these other atom's side like Fig. 3.
(On the opposite side from these atom's nuclei, the carbon's electron orbit tends to be shortened.)
Fig. 3. Estimated ethane (CH3-CH3) model
The C-C bond length of the ethane (CH3-CH3) is about 1.54 × 10-10 meter (=15400 MM)
The above value of the methane (=longest distance between carbon nucleus and electron a) is 7169 MM, which is about half of this C-C bond length ( 15400/2 = 7700 MM )
So this calculation value is thought to be proper, though H and C are different things.
According to the ordinary chemistry, a single bond is said to be formed between two carbon atoms in the ethane.
By the way, what on earth is this "single" bond ??
From this new Bohr model point of view, this C-C single bond can be explained by the existence of one extended carbon's orbit between these two carbon's nuclei like Fig. 3.
The carbon's electron is periodically moving around the nucleus, so it goes back and forth between the "extended" side and "shortened" side of its orbit.
The ethane has six hydrogen's positive nuclei, so only one extended side can exist between two carbon's nuclei at the same time like Fig. 3.
(On the other hand, due to the repulsive Coulomb forces among electrons, when one side orbit is extended, another side orbit is shortened avoiding each other between two carbon's nuclei like Fig. 3.)
The electron on the extended orbit is closer to another carbon's nucleus than that on the shortened orbit.
So, the more "extended" orbits exist between two carbon's nuclei, the stronger the binding force between two carbon's nuclei becomes.
In ethane (CH3-CH3), the "staggered" conformation is a little more stable than "eclipsed one.
But the reason why the "staggered" conformation is more stable is still in controversy.
There are two hypotheses about this reason.
When the ethane is twisted into staggered conformation, the distance between the adjacent hydrogen atoms increases.
So one hypothesis is that the "weakend" repulsive Coulomb interaction between the C-H bonding paris of electrons makes "staggered" conformation more stable.
(But on the other hand, the attractive Coulomb interaction between hydrogen's positive nuclei and electron pairs is also weakened ?)
Another hypothesis is that the interaction between C-H bonding orbital of one carbon and the C-H anti-bonding orbital of another carbon makes the "staggered" conformation more stable.
In both cases, the distance between the hydrogen atoms of different carbons is much longer in comparison to the C-C bond length.
So here we try to seek this reason using the new Bohr's ethane model.
Fig. 4. "Staggered" vs. "Eclipsed" conformations in ethane.
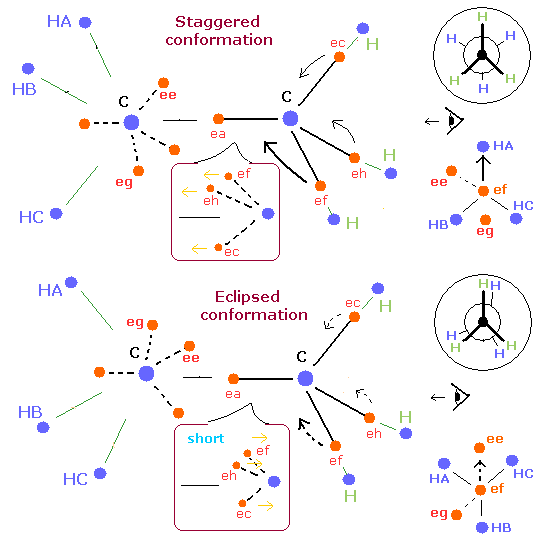
Fig. 4 shows the "staggered" and eclipsed "conformations" of ethane using the new Bohr model and Newman projection.
First, we pay attention to one electron (ef).
In the "staggered" conformation, each hydrogen nucleus of one carbon is arranged in the moving direction of each electron of another carbon.
( ef → HA, eh → HB, ec → HC ).
So, in the "staggered" conformation, the electron ef are moving toward the hydrogen nucleus (HA).
(And the electron eh are moving toward the hydrogen HB.)
On the other hand, in the "eclipsed" conformation, this electron (ef) is not moving toward the hygrogen,
or rather moving away from the hydrogen nucleus (HB).
So, in the "eclipsed" conformation, each electron's orbit between C-C nuclei becomes shorter than that of the "staggered" confomation due to the weaker attractive forces of hydrogen's nuclei.
As a result, these shortened orbits between C-C nuclei make ethane's binding state more unstable.
(It is thought that the influence of these electrons between C-C nuclei are bigger than the interaction between hydrogen atoms which are far away from each other.)
In case of ethane which has six hydrogen atoms, only one extended side can exist between two carbon's nuclei at the same time like Fig. 3.
How about the ethylene (CH2=CH2) ?
The ethylene has four hydrogen atoms which are arranged on the same plane ( x-z plane ).
Usin this new Bohr model, we can express the ethylene correctly like Fig. 5.
Fig. 5. Estimated Ethylene (CH2=CH2) model.
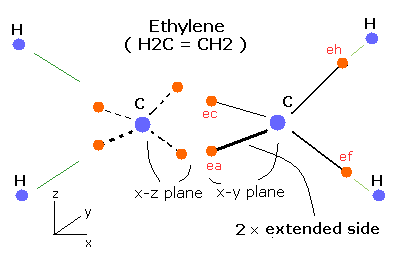
As shown in Fig. 5, the two "extended" orbits can exsist in C=C bond at the same time, which makes the binding energy bigger than C-C bond of ethane.
The four electrons between the two carbon's nuclei are repelling each other.
(Two of them are on the x-z plane, and other two electrons are on the x-y plane like Fig. 5).
In the same way, we can express the acetylene ( HC ≡ CH ) using this Bohr model like Fig. 6.
Fig. 6. Estimated Acetylene (CH ≡ CH) model.
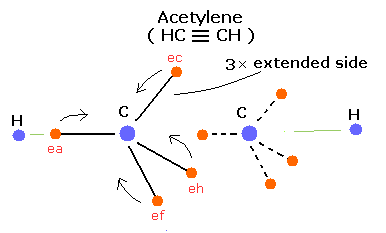
The acetylene has only two hydrogen atoms, so carbon's electrons tend to gather between the two carbon's nuclei.
(In this case, three extended orbits can exist in C ≡ C bond, so the bonding energy becomes more larger.)
It is thought that in C=C bond and C ≡ C bond, "tetrahedral" symmetrical structures change a little, because the two or three electrons are attracted by a single nucleus of another carbon.
So the ethane is more symmetrical than the ethylene and acetylene.
This is why the ethylene and acetylene are more "reactive" than the ethane, though the bonding energies are larger.
For example, the C=C bond of ethylene, H-C-H angle is 117.4 degrees (not 109.5 degrees).
Fig. 7. C=C bond of Ethylene (CH2=CH2).
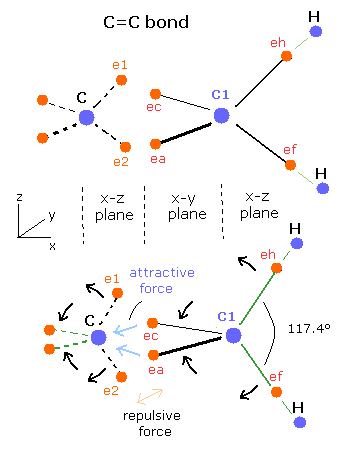
In the C=C bond, the 2 × extended electron (ea, ec) orbits between C=C bond are attracted by a single carbon nucleus (C) as shown in Fig. 7.
So the two electrons (e1, e2) of another side are repelled by the repulsive Coulomb forces, which changes "tetrahedral" symmetrical structure a little.
As a result, the ( eh-C1-ec ) and ( ef-C1-ea ) angles are larger than 109.5 degrees, and to restore its equilibrium, the ( eh-C1-ef ) angle becomes larger than 109.5 degrees, too.
Unfortunatedly, the quantum mechanics can not show as concrete description as our Bohr model.
For example, How do they explain the repulsive forces between C-H bond electrons of both carbons ?
(If we consider this, four hydrogens can not be on the same plane due to the repulsive Coulomb forces like the "staggered" conformation of ethane ?)
And how about the repulsive forces between the π bond electrons and C-H bond electrons ?
And if we consider the repulsive forces between C-H bond electrons (or between the two hydrogen nuclei) of one carbon, H-C-H angle must become larger than 120 degrees ?
The most important thing is that the bonding energy is caused by the fact that electrons are attracted by other atoms' positive nuclei avoiding other electrons.
When the Coulomb attractive forces are stronger than the repulsive forces, the "stable" binding state is formed.
(The energy difference between these attractive and repulsive interactions means "bonding energy".)
But in the ordinary textbooks, the electrons of the π and σ bonds in C=C bond are arranged on the same plane.
(When π and σ bonds are on the x-y planes, all C-H bonds are on the x-z plane in the ordinary quantum chemistry.)
To come near other carbons' positive nuclei avoiding other electrons as much as possible, it is natural that the four electrons of C=C bond are arranged on different planes as shown in our Bohr model.

2010/8/20 updated. Feel free to link to this site.