Estimated Noble gas structure of Bohr model version.
Top page (correct Bohr model including the two-electron atoms).
Strange "Spin" is NOT a real thing.
Bohr model can explain the quantum mechanical variational methods.
The noble (inert) gases such as helium (He), neon (Ne) and argon (Ar), are colourless, odourless and very inactive atoms.
So their atomic structures (configurations) seem to be "symmetrical" and nonpolar.
But only "symmetrical" atomic structure can not explain chemically inactive properties enough.
For example, hydrogen molecule (H2) and methane (CH4) are also colourless, odourless and nonpolar due to their symmetrical structure.
And their melting and boiling points are also low.
But they are highly flammable. (They react with molecules such as oxigen actively.)
So their characteristics can be said to be "active", which is different from the noble gases.
This means that the inactive property of the noble gas in the group 18 of the periodic table needs more explanation other than the symmetrical structure.
(Of course, the "symmetrical" structure is also indispensable. Because if the electrons of the outer shell are unequally distributed, this causes the opening in the shell of the negative charges, which allows this atom to react with other atoms.
The charge of the whole atom is zero, because the magnitude of the nuclear positive charge is equal to that of the sum of the electron's negative charges.
So, to cancel the nuclear positive charge out, the electrons with the same magnitude charge need to be just equally distributed around the nucleus..
If the influence of the nuclear positive charge leaks out, it tends to react with other atoms.)
The standard quantum chemistry (quantum mechanics) says that when the outer shell of valence electrons is considered to be full, it becomes inactive in these elements.
But the quantum chemistry doesn't explain more detailed reason why the outer shell full of electrons causes the inactive property of the noble gas.
In 1920's Bohr model could not explain the ground state ionization energy of the three-body helium atom.
On the other hand, in 1929 Hylleraas succeeded in calculating the approximate value using the variational methods in the Schrodinger equation [1].
His work was the turning point of the history of the quantum mehcanical theory.
But recently we have succeeded in computing the helium ground state energy by the Bohr model based methods using the computer.
(See Top page (correct Bohr model including the two-electron atoms. !)
Now, using the very complicated variational methods, the quantum chemists claim that they have succeeded in calculating the helium ground state energy correctly.
But there are several problems in them.
First, it is very difficult to say that the more than one thousand basis functions express the "real" helium atomic structure.
Second, the latest experimental value of the helium ground state energy (the sum of the ionization energies) is -79.005147 eV ( = 2.903385428 Eh) according to the Nist data.
But the results (-79.01434) of these variational methods are a little different from this correct experimental value.
Because the Shroedinger equation doesn't have the concrete electron orbits, so it can not calculate the nuclear movement correctly.
(In the three-body helium atom, the Schroedinger equation can not judge whether the center of the two electrons is consistent with the nucleus or not due to the lack of the clear orbits.)
Third, in the Schroedinger equation, the probability density near the point at infinity of the ground state electron is NOT zero. ( even in the stable helium atom !).
When the distance between the nucleus and electron becomes longer than some points (in which the potential energy is equal to the total energy), the Coulomb potential energy becomes higher than the ground state energy.
This causes the serious problem. Because at these points, the kinetic energy becomes minus (= 1/2 mv2 < 0 ) !
It is ridiculous ! But the probability density of the electron at these strange points is NOT zero!
(Can you actually imagine these states of MINUS kinetic energy ?)
Next Table shows various works of the calculations of the ground state energy of the helium atom [6].
| Author | Number of basis function | Calculation results (Eh) |
|---|
| Godman, 1998 [2] | 8066 | -2.903724377034119594 |
| Chuluunbaatar et al. 2001 [3] | 5669 | -2.90372437703411959829 |
| Sims and Hangstrom [4] | 4648 | -2.9037243770341195982999 |
| Drake et al. 2002 [5] | 2358 | -2.903724377034119598305 |
| Vladimir I. Korobov 2002 [6] | 5200 | -2.903724377034119598311159 |
| extrap | --- | -2.903724377034119598311 |
As shown in this Table, the variational methods using the Shroedinger equation can not give more correct results than -2.903724377034119598311 ( = -79.014347... eV ). ( The correct experimental value is -79.005147 eV. )
Because these methods can not calculate the effect of the nuclear movement correctly. ( > +0.011eV )
In the helium ion (He+), the relativistic correction to the energy is -0.0028 eV.
The electrons of the neutral helium atom are slower than that of the helium ion. ( and faster than the hydrogen atom. )
So the relativistic correction to the energy is between He+ ( -0.0028 eV ) and the hydrogen atom (-0.000.. eV ).
Our Bohr model based methods have succeeded in getting the more correct results than these complicated variational methods. ( It gives -79.0035..eV. and the relativistic correction is -0.001647 eV !)
Furthermore, the atomic model in which two symmetrical orbits are crossing perpendicularly can explain the stability and closed shell property of the helium atom. (See Top page .)
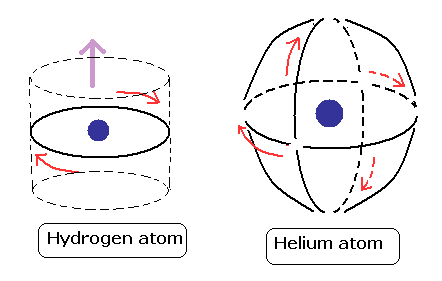
By a computational method, these orbits proved to be just one de Broglie's wavelength.
According to the Pauli exclusion principle, the third electron of the Lithium atom can not get into 1s orbital.
As shown in this figure, there are no more space for the third electron to enter in the Bohr model of helium, because the two orbital planes are just perpendicular to each other.
And Bohr model can solve the various problems of the strange electron spin (See this page !)
In the standard helium atom, the two electrons of 1s orbital are said to have zero angular momentum.
But if so, the two electrons of helium rebound from ( or penetrate through ) the nucleus each time they collide with the nuclues ?
It is a very "unstable" helium atom!
And the standard Helium model has the spin-up and spin-down electrons, so it seems to generate no magnetic fields. But to be precise, the magnetic fields are produced in almost all space, because the two electrons stay apart from each other by the repulsive Coulomb force. So it contains "self-contradiction".
As shown in the methane (CH4), just because the atomic structure is symmetrical and non-polar doesn't mean the strong stability.
The helium atom is NOT only an atom which has two electrons.
To explain this stability, the atom needs other reasons.
See also Why "solitary" helium doesn't form compounds ?.
As shown in the upper figure, the two electrons of our Bohr model are moving periodically in the shell of the stable de Broglie's oscillatory waves.
And the rigorous caluculation results actually indicate the existence of these de Broglie's waves.
In the neon (Ne) and the argon (Ar), it is said that all s and p orbitals are full of electrons.
(The atomic numbers are 10 (Ne) and 18 (Ar), respectively. So both these atoms have just 8 valence electrons in the outer shell.)
But the shape of these s and p orbitals in the Schroedinger equation can not be experimentally confirmed. (This means the shape of these s and p orbitals are only a "mathematical" (not real) thing. )
In the molecules of the ammonia (NH3) and the methane (CH4) (See also this page), the single 2s and the three 2p orbitals mix into four sp3 hybrid orbitals.
By the way, what is this sp3 orbital ?
In NH3, the fourth of the sp3 hybrid orbitals contains the two remaining outer-shell electrons of nitrogen which form a non-bonding lone pair.
These sp3 orbitals are tetrahedral, and geometrically identical due to the repulsive Coulomb force between the pairs of the electrons.
This "tetrahedral" arrangement are very reasonable and can be experimentally confirmed. (This means that this is a "real" thing. )
There is one quention here.
Is the non-bonding electron pair of NH3 originally arranged "tetrahedrally" due to the repulsive Coulomb force ? ( Is it possible that the sp3 hybrid orbitals "originally" exist instead of the "imaginary" 2s and 2p orbitals ? ( especially in the noble (inert) gas such as Ne and Ar ?))
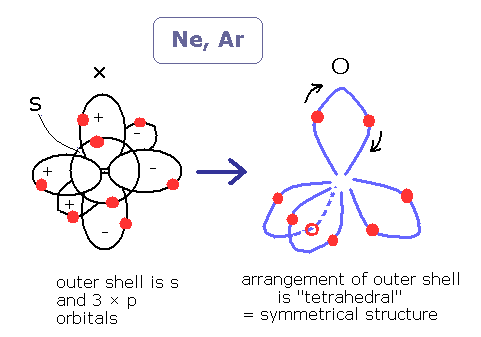
In the noble gas such as neon (Ne) and argon (Ar), the number of the valence electrons is just 8.
So, it is quite natural to think these eight valence electrons (the four electron pairs ) are arranged tetrahedrally in "almost elliptical" orbits.
(2 × tetrahedron becomes hexahedron. ( See also Bohr model Neon page. Neon is a little complicated.)
This structure is just consistent with the Coulomb force condition.
(In the neon and argon, the outer shell orbital is twice or more de Broglie's wavelengh, which is different from the helium atom. So it can be thought that there is space for two electrons. )
As I said, to explain the inactivity of the noble gas, we need to use some forces other than the Coulomb force.
In the noble gas, the stable and symmetrical de Broglie's oscillatory waves (which means it is a integer times de Broglie's wavelength) can be thought to be wrapping the whole atom beutifully.
And considering the number of the valence electrons ( He = 2, Ne and Ar = 8) and the Coulomb force, the above structures are very natural.
[1] E.A. Hylleraas, Z. Physik 54, 347 (1929).
[2] S.P. Gordman, Phys.Rev.A 57 R677 (1998).
[3] O. Chuluunbaatar, I.V. Puzynin, and S.I. Vinitsky, J.Phys.B: At, Mol.Opt.Phys.34,L425 (2001).
[4] J.S. Dims and S.A. Hagstrom, Int. J. Quantum Chem.
[5] G.W.F Drake, N.M. Cassar, and R.A. Nistor, Phys.Rev.A 65, 054051 (2002).
[6] Vladimir I. Korobov, arxiv 0204079v2 (2002)

2010/7/15 updated. Feel free to link to this site.


