
Youhei Tsubono
Top page ( quantum mechanics is false. ← 6/30/2024 )
Bohr Sommerfeld fine structure is right. ← 2023
Pauli exclusion principle by Bohr model is more useful.
Bohr model is the same as the quantum mechanics in all energy levels of the hydrogen atom.
The ordinary textbooks often say that this is only a "accidental" coincidence.
In fact, Schrodinger's hydrogen is one of Bohr-Sommerfeld models also from the "mathematical" viewpoint.
See this page about detailed calculation.
And Schrodinger's hydrogen includes "unreal" states (= minus radial kinetic energy ), which means Schrodinger equation itself is wrong.
(Eq.1) Bohr-Sommerfeld quantization condition.

If we use the de Broglie relation ( wavelength λ = h/p = h/mv , p = momentum ), you can easily find that Bohr Sommerfeld's elliptical orbit is just an integer times de Broglie wavelength.
( Caution: in Eq.1, pr is radial momentum, and "p" means constant angular momentum ( p = r × mv ) ).
To make the ends of wave phases the same in one-round orbit, in both tangential and radial directions, de Broglie waves included in one round must be just integers ( Eq.1 upper = tangential, lower = radial ).
As shown in this section, total de Broglie wave's number is the sum of radial and tangential waves.
(Fig.1) Schrodinger's radial wavefunction is a integer de Broglie wavelength = Sommerfeld's model.
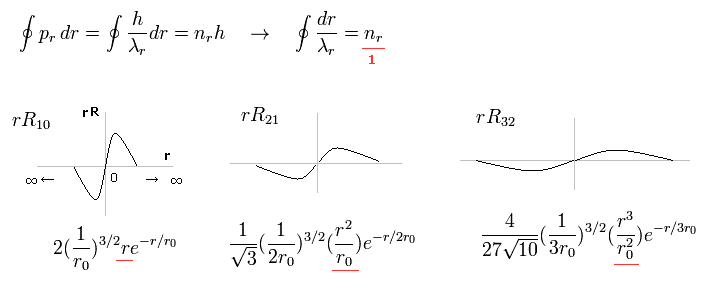
Fig.1 shows the examples of Schrodinger's wavefunctions including one de Broglie wavelength in radial direction of one orbit.
( One orbit means from one point to the same point, ∞ → 0 → ∞ )
For example, R32 wavefunction is "3" principal number ( n = 3 ) and "2" angular (= tangential ) momentum ( l = 2 ).
So the radial wave's number is 3-2= 1.
These wave's numbers have the same meaning as Bohr-Sommerfeld model, which also has an integer de Broglie waves.
( See this page about detailed calculation. )
(Eq.2) de Broglie wave's form in Schrodinger's hydrogen.
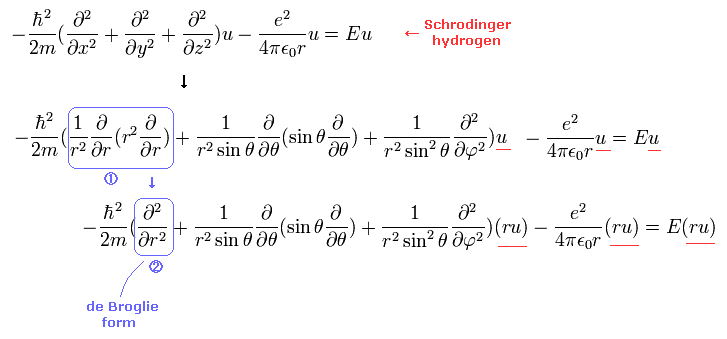
The important point is that we need to express Schrodinger equation as de Broglie wave's form in radial and tangential directions.
(Eq.3)
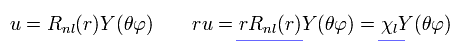
As shown in Eq.2 and Eq.3, if we use χ = rRnl instead of Rnl, this radial wavefunction comes to express de Broglie waves, as shown Fig.1.
(Eq.4)
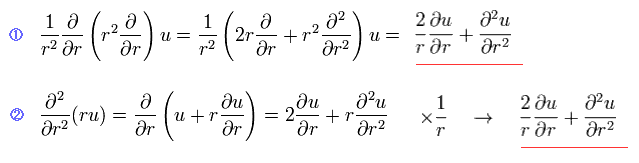
We can easily show Eq.2 transformation is right, using Eq.4.
(Fig.2) Schrodinger's radial wavefunction, two or three waves.
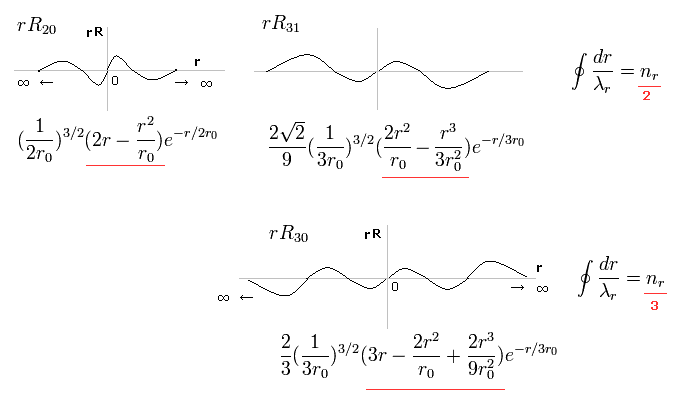
In the upper line of Fig.2, the radial one-round orbits are just two de Broglie wavelength.
For example, in R31, the principal quantum number is "3" and the angular momentum (= tangential ) is "1".
As a result, the radial wave becomes 3-1 = 2 ( which reason is explained later ).
And in the lower wavefunction, n = 3 and l = 0, so the radial wave is 3-0 = 3.
(Fig.3) Schrodinger's tangential wavefunction (= angular momentum ) = Sommerfeld model.

In Fig.3, the angular moementum of Spherical Harmonics in Schrodinger's hydrogen shows the tangential de Broglie wave's number in one orbit.
As a result, the total number of radial and tangential de Broglie waves means the principal quantum number ( n = energy levels ), in both Bohr-Sommerfeld and Schrodinger's models.
(Fig.4)
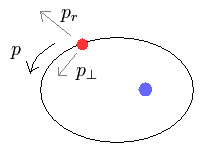
In the elliptical orbits, we can divide the particle's motion into radial and tangential directions at each point.
(Eq.4)
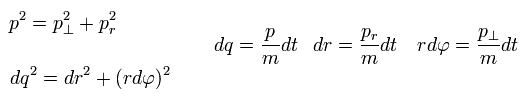
where p means "momentum", and "m" means the particle's mass.
( Only in this section ,"p" means total momentum, which is different from angular momentum of Eq.1 )
And "dq", "dr" and "rdφ" means the distance travelled for the short time dt in each direction.
Of course, the radial and tangential vectors satisfy Pythagorean theorem.
Using de Broglie relation ( wavelength λ = h/p = h/mv ) and Eq.4, the number of de Broglie waves included in the infinitesimal section in each direction is
(Eq.5)
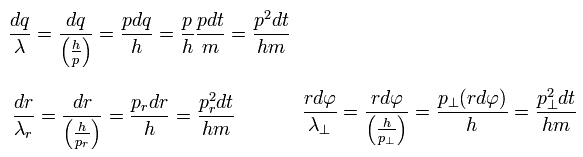
As a result,
(Eq.6)
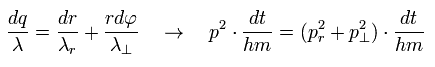
So the total number of de Broglie wave in one orbit is just the sum of radial and tangential waves, ( see also Eq.1 )
(Eq.7)
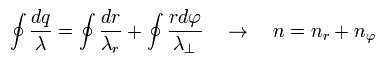
In this section, we review ordinary Bohr model.
First, as shown in this page, Bohr's single electron does NOT fall into nucleus just by acceleration.
(Eq.8)
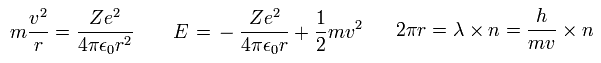
In Eq.8, the first equation means that the centrifugal force is equal to Coulomb force.
The second equation is the sum of Coulomb potential energy and kinetic energy.
The third equation means one circular orbit is an integer (= n ) times de Broglie wavelength.
Substituting the first equation into the second one,
(Eq.9)
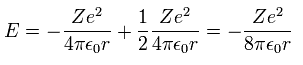
Inserting v of the third equation into the first equation of Eq.8, we have
(Eq.10)
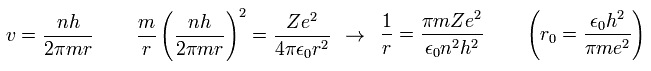
where r0 ( n = Z = 1 ) means "Bohr radius".
Substituting Eq.10 into Eq.9, the total energy E of Bohr model is
(Eq.11)
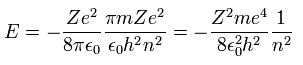
which is the same as Schrodinger's hydrogen.
From Eq.10, the ratio of the particle's velocity v ( n=Z=1 ) to the light speed c is
(Eq.12)
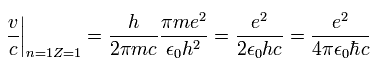
This is the famous fine structure constant α
Bohr-Sommerfeld solution is valid also in the Schrodinger's hydrogen.
The radial quantization number (= nr ) means the number of de Broglie waves included in the radial orbits.
And the nφ means quantized angular momentum (= de Broglie tangential wave's number).
(Eq.13)
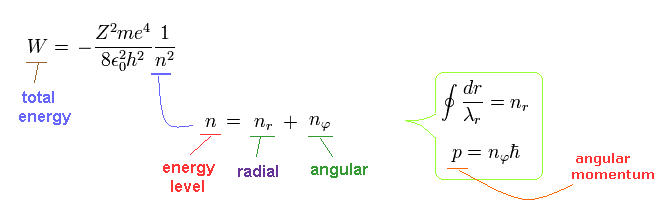
Going back to Fig.1 and Fig.2 of Schrodinger's wavefunction,
(Fig.5) Schorodinger's hydrogen = Bohr Sommerfeld model.
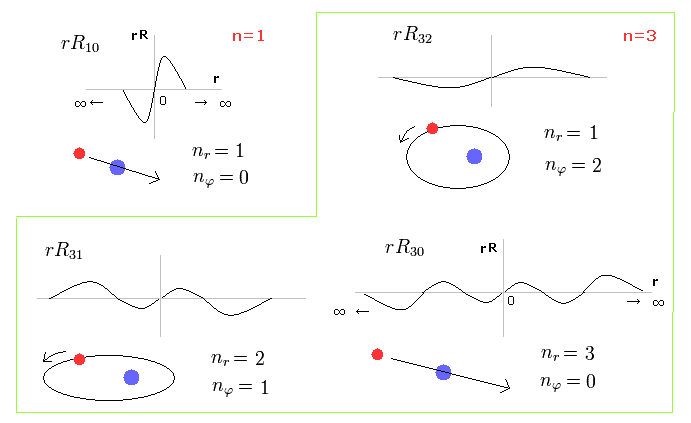
Fig.5 shows the energy levels of Schrodinger's wavefunctions just obey Bohr-Sommerfeld quantization rules.
The most important difference is that Schrodinger's solutions are always from zero to infinity, which is unreal.
If Schrodinger's hydrogen is just circular like Bohr's 1s orbit, its radial wavefunction becomes constant.
In this case, when we normalize it, that wavefunction becomes divergent, when that constant is not zero.
So Schrodinger's wavefunction does NOT include circular orbits, instead, "unreal" zero angular momentum appears.
The fine structure of Bohr-Sommerfeld model is the same as the Dirac equation as shown in this page and this page.
(Fig.6) Accidental coincidence ?
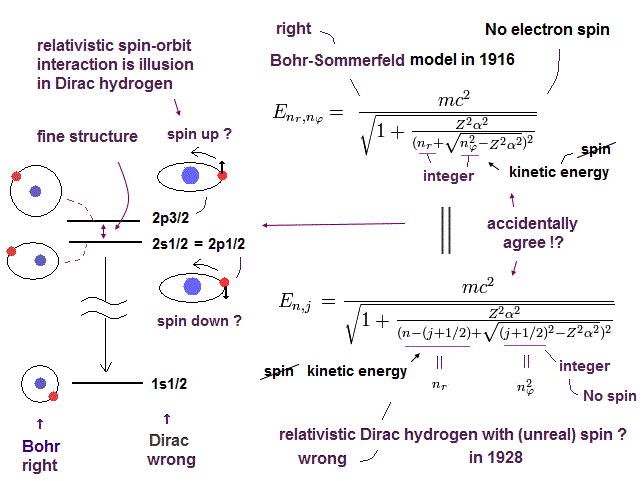
And as shown in this page, fine structure was first explained by Bohr-Sommerfeld model.
Later Dirac's hydrogen was just consistent with Bohr-Sommerfeld model (= Fig.6 ).
Of course, the meanings and mechanisms included in Dirac's hydrogen and Bohr Sommerfeld model are completely different.
But their solutions are completely the same. Why?
Because, they tried to aim at the same solutions as Bohr-Sommerfeld, which was consistent with experimental results, when they thought about Dirac's hydrogen.
Strange to say, Dirac's hydrogen includes many accidental coincidences such as 2S1/2 = 2P1/2, 3S1/2 = 3P1/2, 3P3/2 = 3D3/2 ....
( Dirac's hydrogen needs many "fictional" states. )
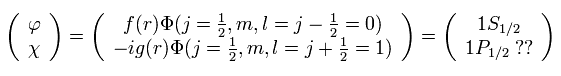
And in fact, Dirac's hydrogen model needs many fictional states to get the solutions (= 1p1/2, 2d3/2, 3f5/2 .... )
( See this page. )
This is clearly inconsistent with the standard quantum mechanics, and shows Dirac's hydrogen is wrong.
If Dirac's hydrogen is wrong, the interpretations such as Lamb shift need to change.
Because the calculation of Lamb shift in QED completely relies on the assumption that Dirac's hydrogen is correct.
If you compare the equations in Fig.6 carefully, you will notice these solutions are the same things.
For example, in the energy level n = 2 of the hydrogen-like atom, the Bohr-Sommerfeld model has the two kinds of the orbitals as follows,
2S orbital = nφ=1, nr=1 ----- elliptical (angular momentum=1)
2P orbital = nφ=2, nr=0 ----- circular (angular momentum =2)
On the other hand, also in the energy level n = 2 of the Dirac hydrogen model, there are two patterns as follows,
2S1/2 , 2P1/2 orbitals----- j = 1/2, n = 2
2P3/2 orbital---- j = 3/2, n = 2
So, the 2S orbital of the Bohr-Sommerfeld model is the same as the 2S1/2 and 2P1/2 orbitals of the Dirac hydrogen model in the energy level.
And the 2P orbital of the Bohr-Sommerfeld model is the same as the 2P3/2 orbital of the Dirac model.
This means that the fine structure is completely the same in both the models. (Only the interpretation of the fine structure is different.)
[1] A. Sommerfeld., Annalen der Physik 1916 [4] 51 p1-94
[2] P.A.M. Dirac., The Principle of Quantum Mechanics (Fourth edition)

2010/4/24 updated. Feel free to link to this site.