3次元トーラス , 四元数多様体 , etc.
3次元トーラスは、トーラスの3次元版です。2次元トーラスは、2次元空間の中では作れず、3次元(以上の)空間の中で
作ることができました(平坦トーラス 参照)。
同様に、3次元トーラスは、3次元空間の中では作れず、4次元(以上の)空間の中で作ることができます。
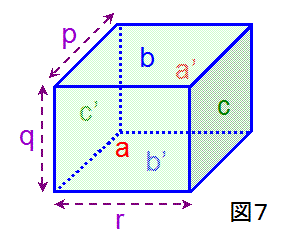
3次元トーラスは、直方体において、対向する面どうしを貼り合わせたものになります。具体的には、図7の直方体において、
面aと面a'を、面bと面b'を、面cと面c'を、それぞれ貼り合わせると、3次元トーラスになります。
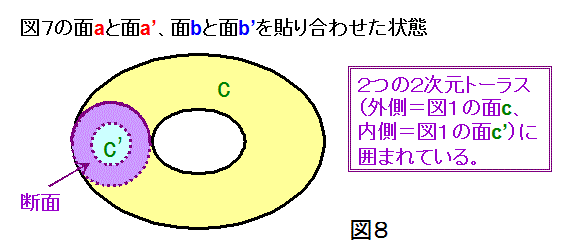
3次元空間の中では、位相を維持しながらの変形を可とするなら、図7の直方体の、面aと面a'、面bと面b'の貼り合わせを
行うことができます。その結果、図8に示すように、2つの2次元トーラスに囲まれた立体が得られます。ここで、外側の
2次元トーラスは図7の面c、内側の2次元トーラスは図7の面c' になっていることがわかります。なお、内側のトーラスは、
ちょっとわかり難いですが、断面で示したように、外側のトーラスとは同心円状になっています。
あと、面c と面c' の貼り合わせを行えば、3次元トーラスができあがります。しかし、図8からわかりますように、面c と面c'
の貼り合わせは、3次元空間ではできません。従って、3次元トーラスは、4次元(以上の)空間の中でしか実現できません。
3次元トーラスは、3次元球面などと同じく、3次元閉多様体の一種です。3次元トーラス中の任意の点は、その周囲に、
3次元的な広がりを持っています。すなわち、3次元トーラスは、3次元球面などと同様、閉じた3次元空間になっており、
3次元的な境界は存在しません。
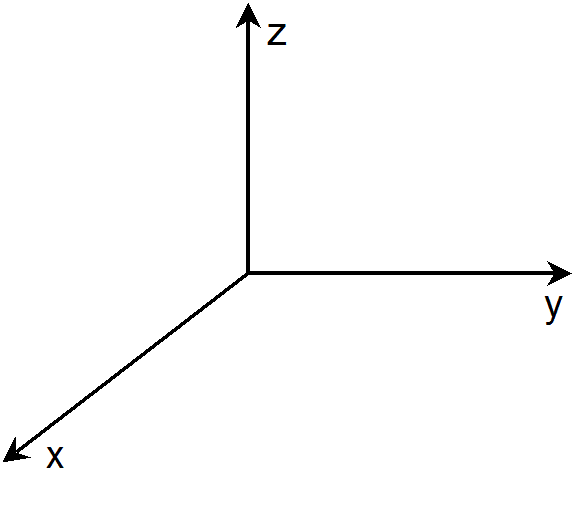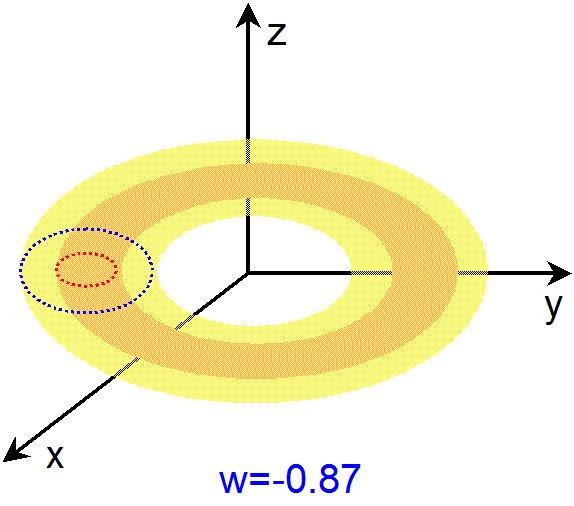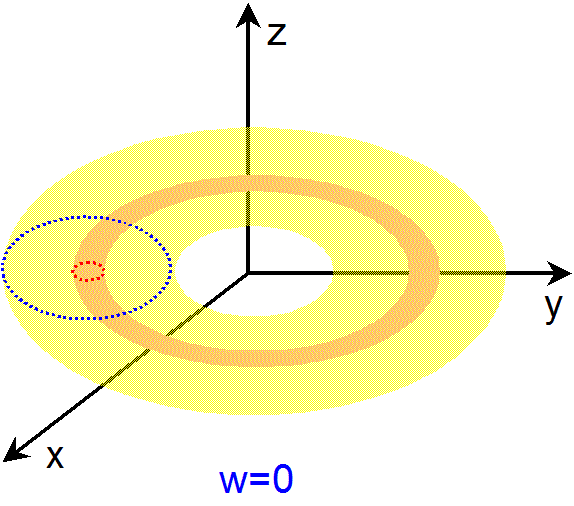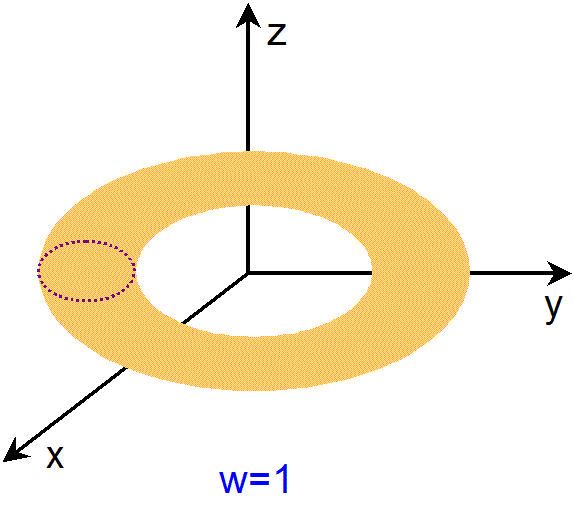
3次元トーラスのGIFアニメーション(GIF animation)を、作ってみました。右のアニメーションです。
まず、アニメーションを構成している各々の図は、4次元空間内にある3次元トーラスを、wをある値に固定した3次元空間で切った断面です。
普通、『断面』と言うと、面(2次元空間)を連想しますが、ここでの断面は、3次元空間です。このアニメーションは、w を -1 から
1 まで変化させながら、各 w での断面(=3次元空間)を次々に示しています。すなわち、右のアニメーションの中で、次々に現れて来る2次元
トーラスは、3次元トーラスの各 w での断面(=3次元空間)を示しています。
アニメーションをご覧になるとわかる様に、まず、w=-1 や w=1 での3次元トーラスの断面は、ともに1個の2次元トーラスで、同じ形をして
います。また、w=a(-1<a<1)での3次元トーラスの断面は、2個の2次元トーラスで、一方の2次元トーラスが他方の2次元トーラスを囲むように
配置されています。そして、w=0 で、2個の2次元トーラスの間の距離が最大になっています。なお、w=-1 や w=1 は、2個の2次元トーラスの
間の距離が 0 になり、1つの2次元トーラスになった状態に他なりません。
ところで、w=-1 から w=0 までの3次元トーラスの各断面は、図8に示した『2つの2次元トーラスに囲まれた立体』を、w=-1 から w=0 までの
4次元空間内に引き伸ばしたものの断面、と考えることができます。同様に、w=0 から w=1 までの3次元トーラスの各断面も、図8に示した
『2つの2次元トーラスに囲まれた立体』を、w=0 から w=1 までの4次元空間内に引き伸ばしたものの断面、と考えることができます。
従って、3次元トーラス(右のアニメーション)は、図8に示した『2つの2次元トーラスに囲まれた立体』を2つ用意して、w=0 において、
その表面どうしを貼り合わせれば、実現できることがわかります。なお、言うまでもありませんが、3次元トーラスの w=0 での断面に現れる2つの
2次元トーラスは、図8の面c と面c' に対応していることがわかります。
ところで、2つの『種数3のハンドル体』の表面どうしを貼り合わせると、3次元トーラスが出来上がります
(*)。『種数3のハンドル体』とは、1個の球体に3個の把手(ハンドル)を付けた形のこと
です。あるいは、穴が3つあるドーナツのような形、と言っても良いでしょう。
(*) 参考書籍 : 『トポロジカル宇宙 [完全版]』 根上生也 著 日本評論社 2007年
次に、3次元平坦トーラスについて考えてみましょう。2次元平坦トーラスは
4次元空間の中で実現できました(平坦トーラス 参照)。同様に、3次元平坦トーラスは、
6次元空間の中で実現することができます。
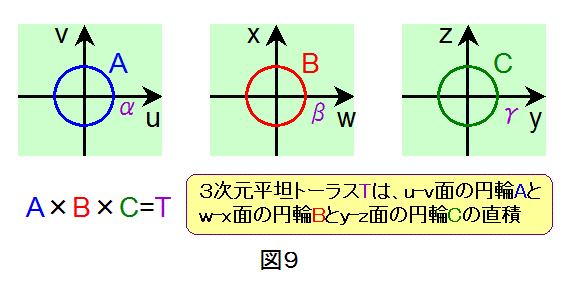
6次元空間を表す6つの座標軸を、u軸、v軸、w軸、x軸、y軸、z軸とします。すると、図9のように、u-v座標系の平面での
円型の輪(1次元)と w-x座標系の平面での円型の輪(1次元)と y-z座標系の平面での円型の輪(1次元)の直積が
2次元平坦トーラスになります。この3次元平坦トーラスを数式で表すと、次式のようになります。
u2+v2=α2, w2+x2=β2, y2+z2=γ2
もし、図9で表した3次元平坦トーラスが、図7の直方体を、伸縮することなく、面a-a'、面b-b'、面c-c'の貼り合わせで
作られているなら、図9の各円輪の半径α、β、γは、図7の直方体の各辺の長さp、q、rの 1/(2π)になります。すなわち、
次式のようになっています。
p=2πα, q=2πβ, r=2πγ
そして、図9の3次元平坦トーラスの体積は、図7の直方体の体積(=pqr)と等しいことがわかります。
なお、平坦な3次元閉多様体は、3次元平坦トーラスだけではありません。例えば、図7の直方体において、q=r とし、
6次元空間の中で、面b-b'、面c-c'の貼り合わせを3次元平坦トーラスと同様に行い、面aを90度回転させて面a'と貼り合わせると、
3次元平坦トーラスとは別の平坦な3次元閉多様体になります(後述の図11 参照)。また、これ以外の貼り合わせ方もあり、結果として、
3次元平坦トーラスを含めて10種類の平坦な3次元閉多様体が構成できます(*)。なお、この10種類のうち、
6種類が向き付け可能な多様体(**)となり、4種類が向き付け不可能な多様体(例えば、後述の図12)となり
ます。
(*) 参考書籍 : 『体験する幾何学』 ヘンダーソン+タイミナ 著 鈴木治郎 訳 ピアソン・エデュケーション社 2010年
(**) この6種類の向き付け可能で平坦な3次元閉多様体は、幾何化予想における8種類の幾何構造の1つである
E3 に分類される多様体です。
さて、冒頭の図7では直方体の対向面の貼り合わせを考えていましたが、これからは、立方体(正六面体)の対向面の貼り合わせを考えることにします。
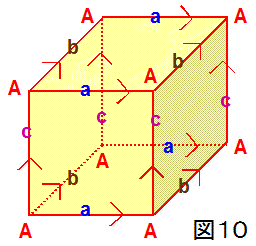
まず、図7の直方体において p=q=r とおくと図10の立方体と等しくなりますから、図10に示すように、この立方体がもつ3組の対向面をそれぞれ
貼り合わせ、その際、対向面の組における各辺の向きが一致するように貼りあわせると、やはり、3次元トーラス(=3次元平坦トーラス)が得られます。
なぜなら、図10からわかるように、8個あった頂点は貼り合わせをすることで1個(図10のA)だけになるからです。具体的に言うと、貼り合わせ後は
8つの頂点立体角が1つの点(図10のA)を囲むことになります。また、立方体の頂点立体角は、π/2 (sr) です。よって、1つの点を囲む8つの頂点立体角
の和は、π/2×8=4π (sr) となります。すなわち、頂点立体角の和が 4π (sr) であることから、この3次元トーラスの幾何構造は平坦であり、
E3 の一種であるとわかります。
なお、3次元トーラスの基本群は、Z×Z×Z ( ただし、Z={ 0, ±1, ±2, ±3, ・・・ } : 整数全体の加法群 )となります。
参考資料: ・Wikipedia 『立体角』
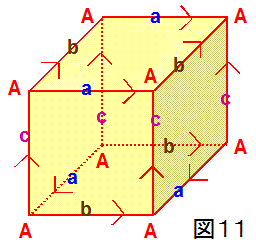 また、前述したように、立方体(または正方形の対面を含む直方体)の対向面の貼り合わせにおいて、1組の対向面(図11における上面と下面)だけ
時計周りに90度回転させて貼り合わせることでも、3次元トーラス(=3次元平坦トーラス)の一種が得られます。
また、前述したように、立方体(または正方形の対面を含む直方体)の対向面の貼り合わせにおいて、1組の対向面(図11における上面と下面)だけ
時計周りに90度回転させて貼り合わせることでも、3次元トーラス(=3次元平坦トーラス)の一種が得られます。
なぜなら、図11からわかるように、図10と同様に、8個あった頂点は貼り合わせ後は1個(図11のA)だけになり、頂点立体角の和が 4π (sr) に
なるからです。よって、この3次元閉多様体も、幾何構造は平坦であり、E3 の一種であることが
わかります。
なお、図10や図11に示した3次元閉多様体の辺の個数に注目すると、もともとあった12本の辺は貼り合わせ後、4分の1の3本(図10、図11の
a、b、c)だけになります。すなわち、貼り合わせ後は、4つの辺が1辺になり、その1辺の周囲を4つの直角(=π/2 rad )が囲むことになるため、
その平面角の和は、π/2×4=2π (rad) となります。よって、このことからも、これらの3次元閉多様体の幾何構造が平坦であるとわかります。
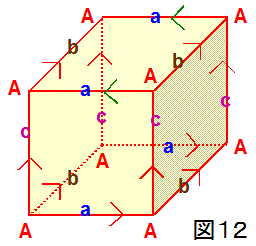 つぎに、立方体において、4つの側面は図10と同様の貼り合わせをするが、上面は裏返してから下面と貼り合わせる場合について、考えてみましょう。
この場合、図12に示したように、上面の辺aの向き(=『緑色』の矢印)と下面の辺aの向き(=『赤色』の矢印)が逆になるため、貼り合わせにより
得られる3次元閉多様体は『クラインの壺の3次元版』になります。すなわち、3次元トーラスと同じく平坦な3次元閉多様体ではあるが、向き付けが
不可能な多様体となります。なお、向き付けが不可能であることは、図12において、正四面体を3次元多様体(立方体)の内部→上面→下面→内部へ
移動させることで確かめることができます(『ギーゼキング多様体 と レンズ空間』 参照)。
つぎに、立方体において、4つの側面は図10と同様の貼り合わせをするが、上面は裏返してから下面と貼り合わせる場合について、考えてみましょう。
この場合、図12に示したように、上面の辺aの向き(=『緑色』の矢印)と下面の辺aの向き(=『赤色』の矢印)が逆になるため、貼り合わせにより
得られる3次元閉多様体は『クラインの壺の3次元版』になります。すなわち、3次元トーラスと同じく平坦な3次元閉多様体ではあるが、向き付けが
不可能な多様体となります。なお、向き付けが不可能であることは、図12において、正四面体を3次元多様体(立方体)の内部→上面→下面→内部へ
移動させることで確かめることができます(『ギーゼキング多様体 と レンズ空間』 参照)。
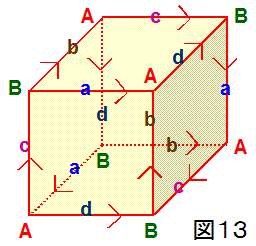
ところで、立方体の貼り合わせにおいて、1組だけでなく3組の対向面を全て90度回転させて貼り合わせた場合、どんな3次元多様体が得られるで
しょうか? この点について考えてみましょう。
具体的には、立方体の3組の対向面のそれぞれについて、時計回りに90度回転させて順に貼り合わせて行くと、図13のような3次元多様体が得られます。
すなわち、貼り合わせにより、8個あった頂点は2個(図13のA、B)だけにになり、12本あった辺は4本(図13のa、b、c、d)だけになります。
よって、頂点の個数は貼り合わせによって8個の4分の1の2個になるから、貼り合わせ後の頂点1個の周囲を4つの頂点立体角が囲むことになります。
また、立方体の頂点立体角は、π/2 (sr) です。よって、1つの点を囲む4つの頂点立体角の和は、π/2×4=2π<4π (sr) となります。すなわち、
頂点立体角の和が 4π (sr) より小さいことから、この3次元多様体は球面幾何をもつ多様体(S3等 の
一種)であるとわかります。
なお、図13の3次元多様体の辺の個数に注目すると、もともとあった12本の辺は貼り合わせ後、3分の1の4本(図13のa、b、c、d)だけに
なります。すなわち、貼り合わせ後は、3つの辺が1辺になり、その1辺の周囲を3つの直角(=π/2 rad )が囲むことになるため、その平面角の和は
π/2×3=3π/2<2π (rad) となります。よって、このことからも、この3次元多様体の幾何構造が球面的であるとわかります。
また、この3次元多様体は、基本群が四元数群 Q8 (={ ±1, ±i, ±j, ±k } : 四元数の単位の乗法群(位数8))
となるので、四元数多様体と呼ぶこともできるでしょう。
参考資料: ・下記URLに掲載のPDFファイル
http://www2.itc.kansai-u.ac.jp/~wakui/sotsuron_syouji.pdf#search=%27%E6%AD%A3%E5%A4%9A%E9%9D%A2%E4%BD%93%E3%81%AE%E5%9B%9E%E8%BB%A2%E3%81%AB%E3%82%88%E3%82%8B%E5%95%86%E7%A9%BA%E9%96%93%E3%81%AE%E5%9F%BA%E6%9C%AC%E7%BE%A4%27
・下記URLに掲載のPDFファイル
https://pi.math.cornell.edu/~hatcher/AT/AT.pdf#search=%27Allen+Hatcher+Algebraic+Topology%27
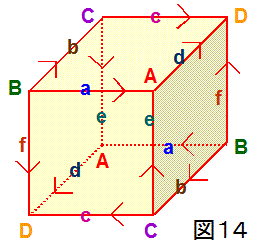
さらに、立方体の3組の対向面を全て180度回転させて貼り合わせた場合を考えると、上記のいずれとも異なる別の3次元多様体が得られます。
具体的に言うと、立方体の3組の対向面のそれぞれを180度回転させて順に貼り合わせて行くと、図14のような3次元多様体が得られます。すなわち、
貼り合わせにより、8個あった頂点は4個(図14のA、B、C、D)だけにになり、12本あった辺は6本(図14のa、b、c、d、e、f)だけに
なります。よって、頂点の個数は貼り合わせによって8個の2分の1の4個になるから、貼り合わせ後の頂点1個の周囲を2つの頂点立体角が囲むことに
なり、立方体の頂点立体角が π/2 (sr) であるから、1つの点を囲む4つの頂点立体角の和は π/2×2=π<4π (sr) となります。すなわち、
頂点立体角の和が 4π (sr) より小さいことから、この3次元多様体は球面幾何をもつ多様体(S3等 の
一種)であるとわかります。
そして、このように立方体の3組の対向面を180度回転して貼りあわせた3次元多様体は、3次元実射影空間(=レンズ空間 L(2,1) )に他ならないことも
わかります(『ギーゼキング多様体 と レンズ空間』など 参照)。
なお、図14の3次元多様体の辺の個数に注目すると、もともとあった12本の辺は貼り合わせ後、2分の1の6本(図14のa、b、c、d、e、f)だけ
になります。すなわち、貼り合わせ後は、2つの辺が1辺になり、その1辺の周囲を2つの直角(=π/2 rad )が囲むことになるため、その平面角の和は
π/2×2=π<2π (rad) となります。よって、このことからも、この3次元多様体(=3次元実射影空間)の幾何構造が球面的であるとわかります。
また、この3次元実射影空間(=レンズ空間 L(2,1) )の基本群は、Z2 (={ ±1 } : 位数2の巡回群 )となります。





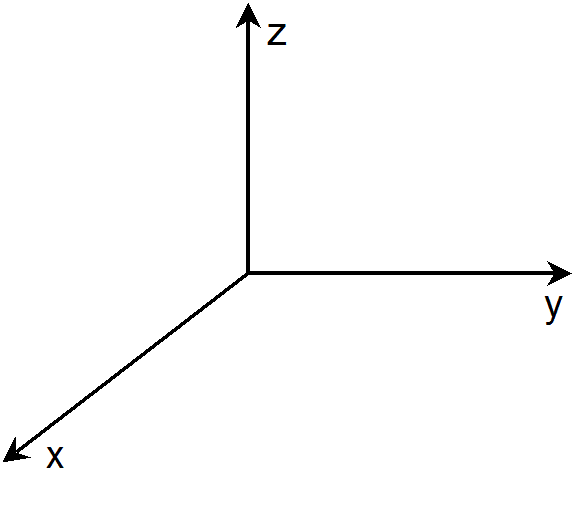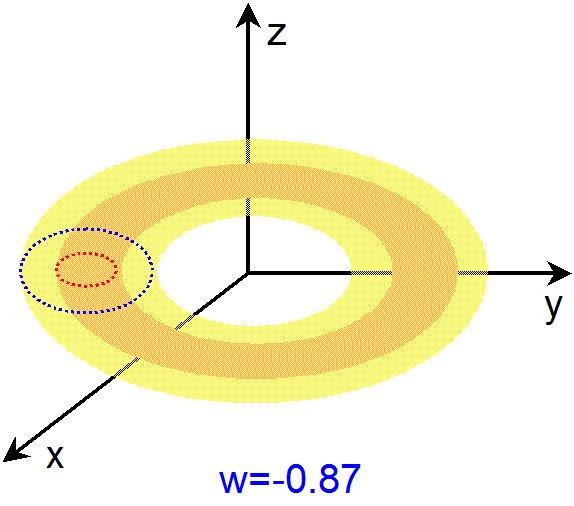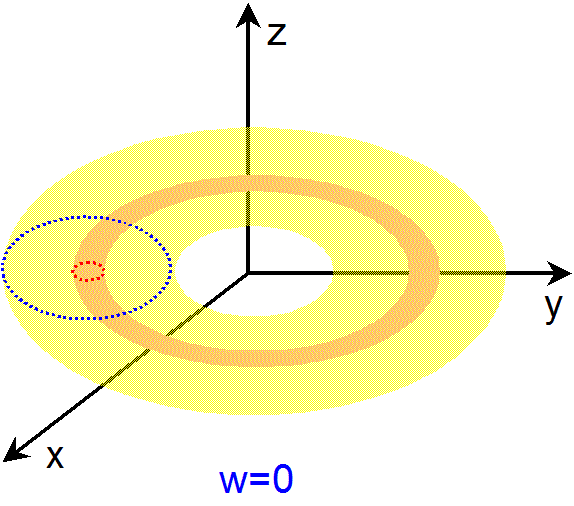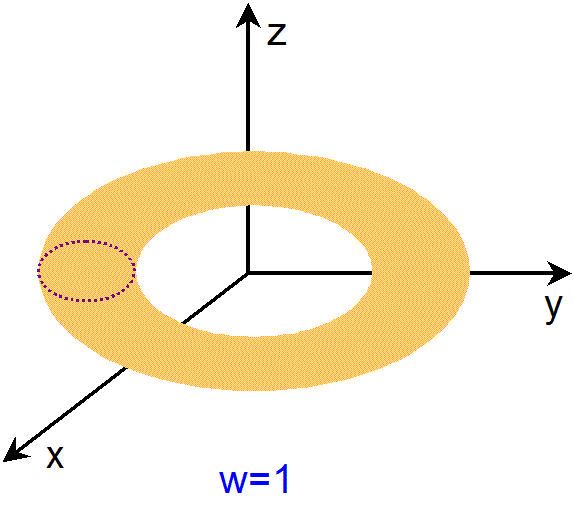


 また、前述したように、立方体(または正方形の対面を含む直方体)の対向面の貼り合わせにおいて、1組の対向面(図11における上面と下面)だけ
時計周りに90度回転させて貼り合わせることでも、3次元トーラス(=3次元平坦トーラス)の一種が得られます。
また、前述したように、立方体(または正方形の対面を含む直方体)の対向面の貼り合わせにおいて、1組の対向面(図11における上面と下面)だけ
時計周りに90度回転させて貼り合わせることでも、3次元トーラス(=3次元平坦トーラス)の一種が得られます。
 つぎに、立方体において、4つの側面は図10と同様の貼り合わせをするが、上面は裏返してから下面と貼り合わせる場合について、考えてみましょう。
この場合、図12に示したように、上面の辺aの向き(=『緑色』の矢印)と下面の辺aの向き(=『赤色』の矢印)が逆になるため、貼り合わせにより
得られる3次元閉多様体は『クラインの壺の3次元版』になります。すなわち、3次元トーラスと同じく平坦な3次元閉多様体ではあるが、向き付けが
不可能な多様体となります。なお、向き付けが不可能であることは、図12において、正四面体を3次元多様体(立方体)の内部→上面→下面→内部へ
移動させることで確かめることができます(『ギーゼキング多様体 と レンズ空間』 参照)。
つぎに、立方体において、4つの側面は図10と同様の貼り合わせをするが、上面は裏返してから下面と貼り合わせる場合について、考えてみましょう。
この場合、図12に示したように、上面の辺aの向き(=『緑色』の矢印)と下面の辺aの向き(=『赤色』の矢印)が逆になるため、貼り合わせにより
得られる3次元閉多様体は『クラインの壺の3次元版』になります。すなわち、3次元トーラスと同じく平坦な3次元閉多様体ではあるが、向き付けが
不可能な多様体となります。なお、向き付けが不可能であることは、図12において、正四面体を3次元多様体(立方体)の内部→上面→下面→内部へ
移動させることで確かめることができます(『ギーゼキング多様体 と レンズ空間』 参照)。


