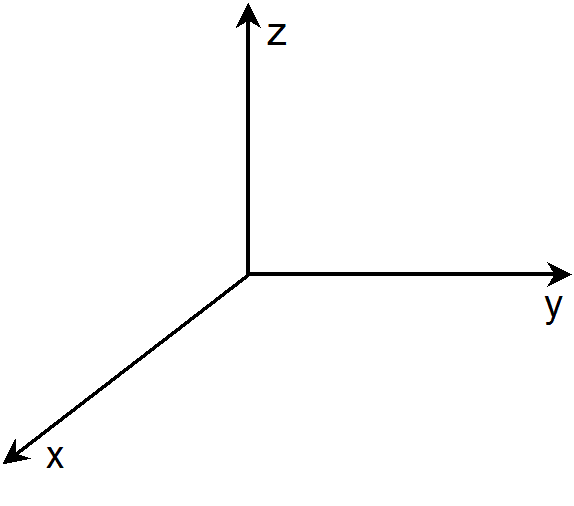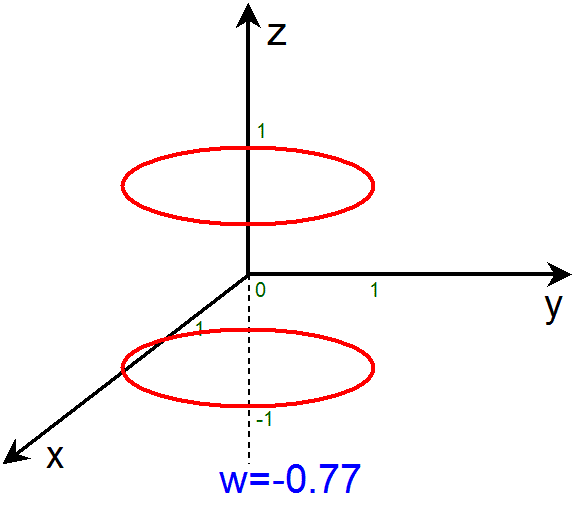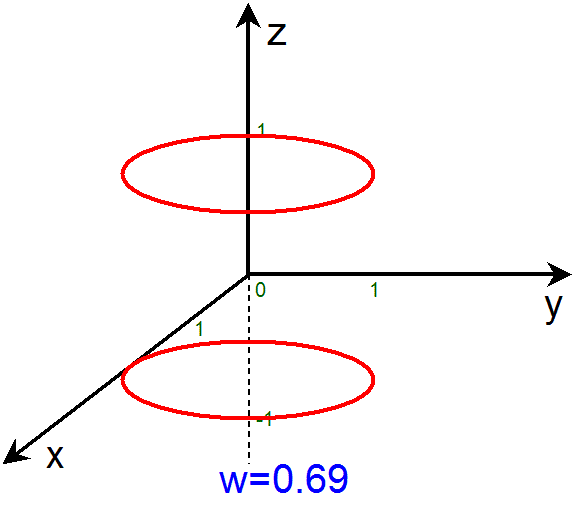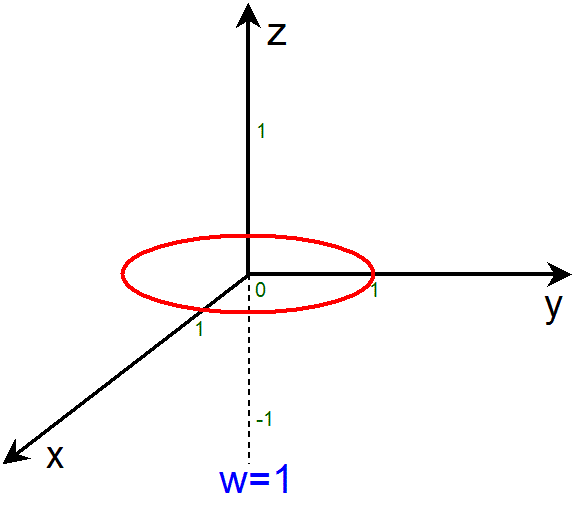平坦トーラス
いわゆるドーナツや浮き輪のような形を、トポロジー（位相幾何学）では、トーラス（torus）（正確には２次元トーラス）と
呼んでいます。ご存知のように、ふつう我々が目にしているトーラス（ドーナツや浮き輪のような形）は、ぐにゃりと曲がって
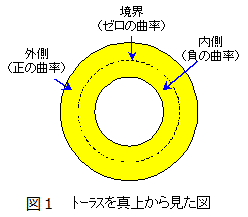
います。少し数学的に言うと、外側で正の曲率、内側で負の曲率、その境界でゼロの曲率になっています
（図１参照）。
また、容易にわかることですが、２次元トーラスは、２次元空間の中では作れず、３次元（以上の）空間の中で作ることができます。
ところで、すべての場所でゼロの曲率になっているトーラスのことを、平坦トーラス（flat torus）と呼んでいます。
残念ながら、我々が生活している３次元空間の中では、ゼロの曲率を維持したトーラス（＝２次元平坦トーラス）を作ることが
できません。実は、２次元平坦トーラスは、４次元（以上の）空間の中でしか、実現できないのです。
まず、２次元トーラスを作ってみましょう。図２に示した長方形において、
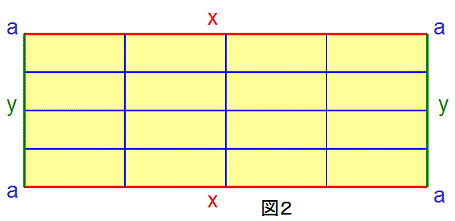
４つの点“a”が、同一の点になるように、
２つの線“x”が、同一の線になるように、
２つの線“y”が、同一の線になるように、
折り曲げると、２次元トーラスができあがります。しかし、３次元空間の中で、このような折り曲げを行うと、
どうしても、面の伸縮をせざるを得ません。そして、面の伸縮を行った結果、図１のように、曲率がゼロでなくなってしまいます。
面の伸縮なしで折り曲げられた曲率ゼロのトーラス、すなわち、２次元平坦トーラスは、３次元空間の中では実現できないことが
わかるかと思います。
では、４次元空間の中で、２次元平坦トーラスを作ってみましょう。
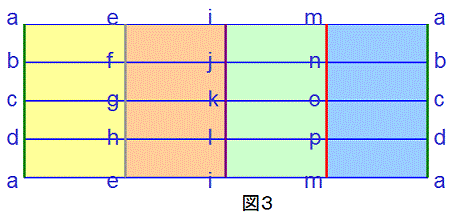
図３は、前述の長方形（図２）と基本的には同じものですが、以下の説明のために、記号や色分けを変えたものです。
まず、この長方形を、色分けされた領域で縦に４分割し、各領域の上辺と下辺を接合すると、４つの角柱状の筒型ができます。
次に、これらの４つの角柱状の筒型を、４次元空間の中でつなぎ合わせてみましょう。なお、４次元空間（より正確に言うと、
４次元ユークリッド空間）を表す４つの座標軸を、x軸、y軸、z軸、w軸とします。
図４−１は、図３の左端の領域から作った筒型を、w=w0 での x-y-z座標系に配置していることを示しています。
なお、筒型の両端のy座標は、y=y0、y=y1 となっているとします。
図４−２は、図３の左から２番目の領域から作った筒型を、y=y1 での x-z-w座標系に配置していることを示しています。
なお、筒型の両端のy座標は、w=w0、w=w1 となっているとします。
図４−３は、図３の左から３番目の領域から作った筒型を、w=w1 での x-y-z座標系に配置していることを示しています。
なお、筒型の両端のy座標は、y=y0、y=y1 となっているとします。
図４−４は、図３の左から４番目の領域から作った筒型を、y=y0 での x-z-w座標系に配置していることを示しています。
なお、筒型の両端のy座標は、w=w0、w=w1 となっているとします。
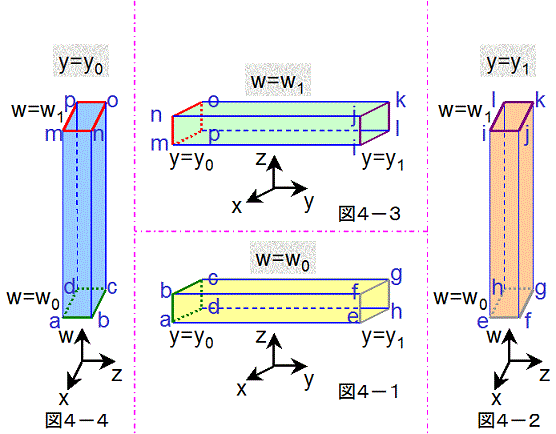
図４−１〜図４−４を見比べると、４つの筒型の端は、順番につなぎ合わされていることがわかると思います。まず、図４−１の
筒型の右端（点e、f、g、hを結ぶ、灰色の閉曲線）では y=y1, w=w0 ですが、図４−２の筒型の下端でも
y=y1, w=w0 なので、２つの端どうしの位置が一致しています。すなわち、この２つの端はつなぎ合わされて
いることがわかります。そこで、図４−２の筒型の下端も、e、f、g、hを結ぶ、灰色の閉曲線として表しています。同様に、図４−２の
筒型の上端と図４−３の筒型の右端（i-j-k-l：紫色）も、ともに y=y1, w=w1 なので、この２つはつなぎ合わ
されています。さらに、図４−３の筒型の左端と図４−４の筒型の上端（m-n-o-p：赤色）も、ともに y=y0, w=w1
なので、つなぎ合わされています。最後に、図４−４の筒型の下端と図４−１の筒型の左端（a-b-c-d：緑色）も、ともに y=y0,
w=w0 なので、つなぎ合わされています。
結局、図４の４つの筒型の端どうしは順番につなぎ合わせれているので、２次元トーラスを形成していることがわかります。しかも、
面の伸縮なしで実現されているので、２次元平坦トーラスとなっています。
なお、図４−１〜図４−４の４つの筒型がどのように接続されているかと言うと、図４−１の筒型の外側の面が図４−２の筒型の内側の面
とつながり、図４−２の筒型の内側の面が図４−３の筒型の内側の面とつながり、図４−３の筒型の内側の面が図４−４の筒型の外側の面と
つながり、図４−４の筒型の外側の面が図４−１の筒型の外側の面とつながっています。
すなわち、このようにして構成されたトーラスは、表と裏の区別のある閉曲面となっていることがわかります。
したがって、図４−１の筒型の外側の面上のある点から筒型の長手方向に線を引いていくと、その線は、一回りの閉じた線となり、
図４−１と図４−４では筒型の外側の面上にあり、図４−２と図４−３では筒型の内側の面上にあります。
このように、４次元空間内の２次元平坦トーラスは、図１のような３次元空間内の２次元トーラスと同様
に表と裏の区別のある閉曲面となりますが、外側の面と内側の面の区別がないと言う点では図１のような
トーラスと異なります。
ところで、４次元空間内の２次元トーラスについては、２次元トーラスに囲まれた３次元または４次元の領域は存在しません。例えば、
図４−１の筒型について、左側から筒型の内側の空間を通過して右側へ抜ける経路を考えてみましょう。その経路は、トーラスの内側の空間
を通過しますが、トーラスを横切りません。このように、４次元空間では、我々が生活している３次元空間では有り得ないことが起こります。
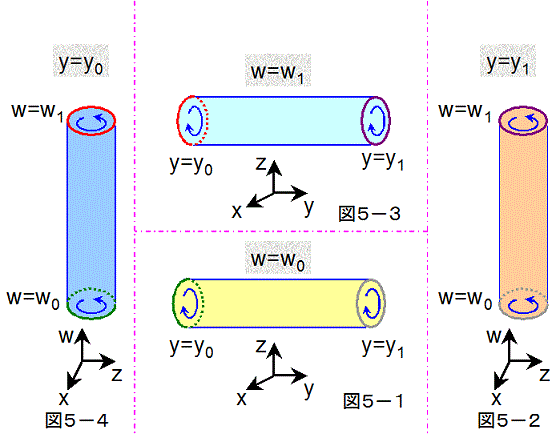今度は、円柱状の筒型を用いて、上述と同様の方法で、２次元平坦トーラスを作ってみましょう。
図５では、図４のそれぞれの筒型を、角柱状から円柱状に変えただけです。４つの筒型のつなぎ合わせ方は、今回も同様です。
同じ色の端どうしを、図中の青い矢印の向きに合わせてつなげば、２次元平坦トーラスができあがります。
また、図４と場合と同様、図５−１の筒型の外側の面が図５−２の筒型の内側の面とつながり、図５−２の筒型の内側の面が図５−３の
筒型の内側の面とつながり、図５−３の筒型の内側の面が図５−４の筒型の外側の面とつながり、図５−４の筒型の外側の面が図５−１の
筒型の外側の面とつながっていることがわかります。
なお、参考までに、図４（図５）における４つの角柱（円柱）のつなぎ方を１箇所だけ変えると、平坦トーラスではなく
平坦なクラインの壺になります。
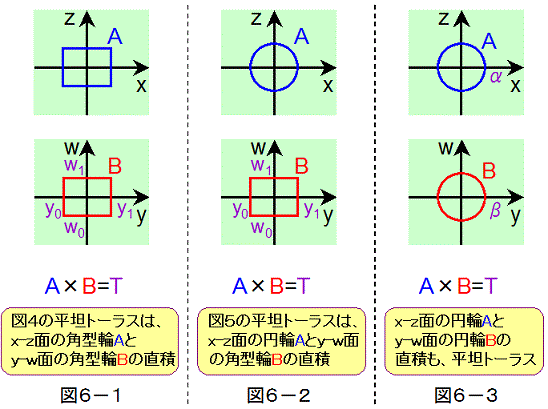
ところで、図４の２次元平坦トーラスは、図６−１のように、x-z座標系の平面での角型の輪（１次元）と、y-w座標系の平面での
角型の輪（１次元）の直積で表すことができます。また、図５の２次元平坦トーラスは、図６−２のように、x-z座標系の平面での
円型の輪（１次元）と、y-w座標系の平面での角型の輪（１次元）の直積で表すことができます。
同様に考えると、図６−３のように、x-z座標系の平面での円型の輪（１次元）と、y-w座標系の平面での円型の輪（１次元）の直積も、
２次元平坦トーラスになることがわかります。この２次元平坦トーラスを図４や図５のような図で表すのは難しいので、数式で表すこと
にすると、次式のようになります。
x2+z2=α2, y2+w2=β2
なお、図６−３を拡張することで、３次元平坦トーラスを表すことができます。
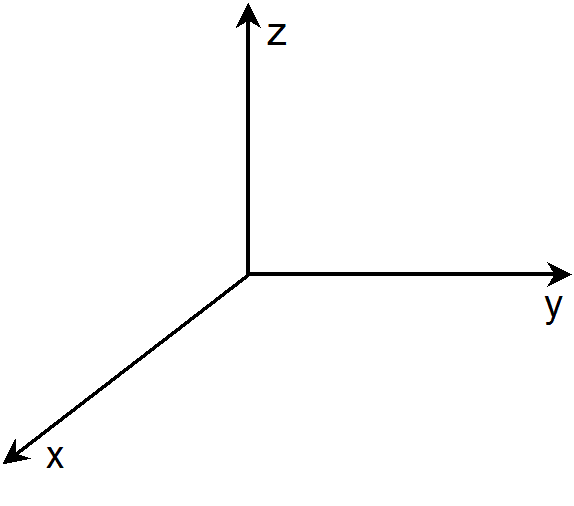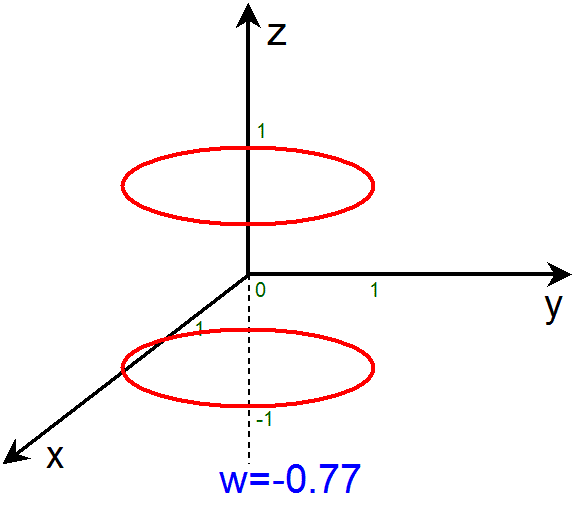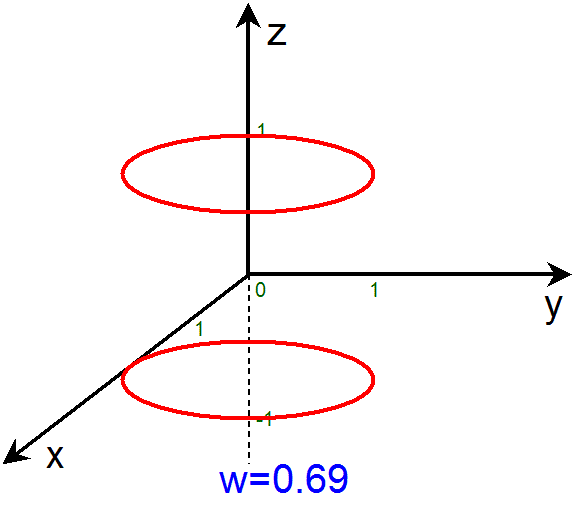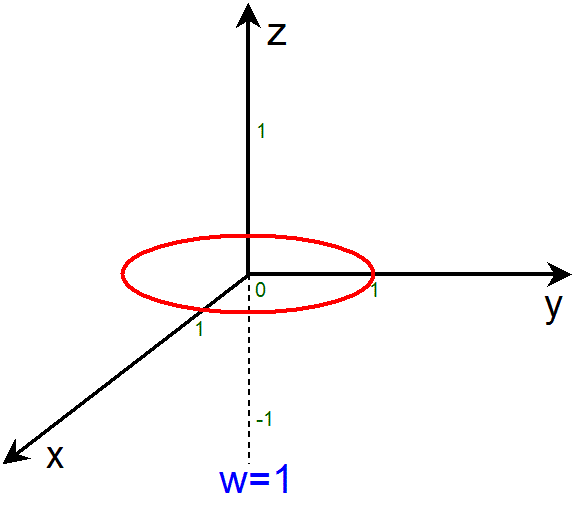
図６−３の２次元平坦トーラスのＧＩＦアニメーション（GIF animation）を作ってみました。右のアニメーションです。
w軸を時間軸に置き換えて、アニメーションにしてみました。２次元平坦トーラスの形状をイメージするのに、少しは役に立つのでは、と思います。
なお、このアニメーションは、図６−３で y軸と z軸を入れ換えた場合に対応しています。軸の入れ換えを行っても、本質的には同じなので、特に
気にする必要はありません。
では、このアニメーションについて、説明します。
まず、アニメーションを構成している各々の図は、４次元空間内にある２次元平坦トーラスを、wをある値に固定した３次元空間で
切った断面です。普通、『断面』と言うと、面（２次元空間）を連想しますが、ここでの断面は、３次元空間です。
このアニメーションは、w を -1 から 1 まで変化させながら、各 w での断面（＝３次元空間）を次々に示しています。そして、各断面での
赤い輪は、２次元平坦トーラスの各 w での断面です。この赤い輪は、いずれも、z がある値に固定された x-y平面の上にある、半径１の円です。
アニメーションをご覧になるとわかる様に、例えば、w＝-1 や w＝1 での２次元平坦トーラスの断面は１つの輪で、z＝0 での x-y平面の上に
ある円です。また、w＝0 での断面は２つの輪で、z＝-1 での x-y平面の上にある円と、z＝1 での x-y平面の上にある円です。
そして、w＝a（-1＜a＜1）での断面は２つの輪で、z＝-(1-a2)1/2 での x-y平面の上にある円と、
z＝(1-a2)1/2 での x-y平面の上にある円です。
ここで、z と w の関係に注目すると、z2＋w2＝1 の関係を保ちながら、z と w は変化していることがわかります。
すなわち、z-w平面の上にある、半径１の円の上を動いていることになります。従って、２次元平坦トーラスは、x-y平面の上にある円が、z-w平面
の上にある円の上を動いた軌跡に他なりません。
ところで、x軸の代りに z軸、y軸の代りに w軸、z軸の代りに x軸に、それぞれ置き換え、w軸ではなく y軸を時間軸とするアニメーションを
作った場合でも、右のアニメーションと全く同じ様に、赤い輪が動きます。すなわち、２次元平坦トーラスは、z-w平面の上にある円が、x-y平面の
上にある円の上を動いた軌跡にもなっているのです。
なお、４次元空間内で、１辺が 2π の正方形（図２の長方形で、辺 x と辺 y の長さを 2π
にした場合）を、伸縮することなく、かつ、ゼロの曲率を維持したまま、向かい合った辺どうしを接合すると、右のアニメーションが表す
２次元平坦トーラスになります。
