幾何化予想とポアンカレ予想

　サーストンの幾何化予想によれば、素分解（prime decomposition）後に得られる向き付け可能な閉３次元多様体 （oriented prime closed 3-manifold）は、下記の８種類の幾何構造（geometric structure）を有する多様体のいずれかになります。 （*）
  1. S3等　　 ：　３次元球面（S3）、ポアンカレ球面、レンズ空間、等 （関連ページ）　３次元球面 と Ｓ2ＸＳ1 多様体 　ポアンカレ球面・ザイフェルトウェーバー多様体 etc.
  2. E3　　　 ：　３次元トーラス（S1×S1×S1）、等 　　　　　　　　 （関連ページ）　３次元トーラス , 四元数多様体 , etc.
  3. H3　　　 ：　３次元双曲多様体　　　　　　 　　　　　　　　　　 （関連ページ）　ポアンカレ球面・ザイフェルトウェーバー多様体 etc.
  4. S2×R　　：　球面と輪の直積（S2×S1） 　　　　　　　　　　　　 （関連ページ）　３次元球面 と Ｓ2ＸＳ1 多様体
  5. H2×R　　：　双曲面と輪の直積（H2×S1）
  6. SL2(R)　 ：　ブリースコーンホモロジー球面
  7. Nil　　 　：　２次元トーラスのデーンツイストの写像トーラス
  8. Sol　　　：　２次元トーラス上のアノソフ写像の写像トーラス

　　　（*） 参考資料　：　Wikipedia　『幾何化予想』


Ｓ３と他の３次元多様体の違い 　サーストンの幾何化予想は、1982年に米国の数学者サーストンが発表したもので、その後、多くの数学者により その証明が試みられ、最終的には 2003年発表のペレルマンの論文により証明されました。このように、幾何化予想は、 正しいことが証明されているので、幾何化定理と呼んでも良いものです。

　なお、1904年にフランスの数学者ポアンカレが予想した、有名なポアンカレ予想は、サーストンの幾何化予想から 派生的に導かれるので、ペレルマンの論文は、ポアンカレ予想をも証明したことになります。

　なぜ、ポアンカレ予想も証明されたことになるかと言うと、素分解後の３次元多様体のうち、Ｓ３（＝ 1 の S3 ） と それ以外 の多様体（＝ 1 の S3以外 と 2 〜 8 ） では、基本群が異なるからです。Ｓ３の基本群は自明な群（群の元は単位元のみ） ですが、Ｓ３以外の３次元多様体の基本群は自明な群ではない（群の元は単位元を含む複数の元からなる）からです。

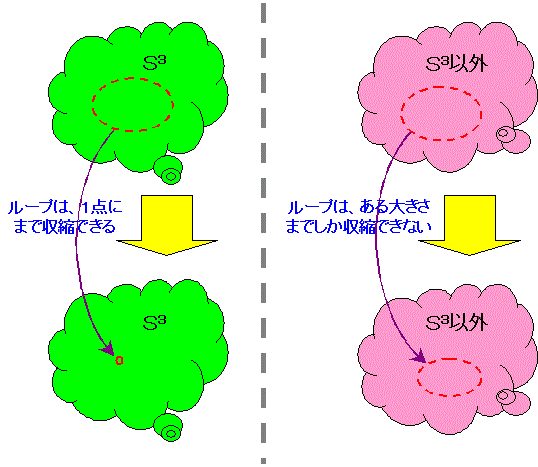
　このことを、簡単な図で説明します。右図のように、Ｓ３の内部にある任意のループは、１点に収縮することが できます。１点に収縮できるループとは、単位元を意味します。しかし、Ｓ３以外の３次元多様体では、 １点に収縮できないループ（※）が必ず存在します。このようなループは、単位元ではない元を 表します。
　　（※） 例えば、S2×S1多様体には、１点に収縮できないループが必ず存在します。 → 関連ページ

　すなわち、Ｓ３とそれ以外では、基本群が異なります。

　ポアンカレ予想は、『基本群が自明な群である３次元多様体はＳ３のみ』と言う内容だったので、以上から、 幾何化予想はポアンカレ予想を包含していることがわかります。

　ところで、ペレルマンの証明により、全ての次元において成り立つことが証明された「一般化されたポアンカレ予想」とは、「位相同相（Topological 同相） を前提とした一般化されたポアンカレ予想」のことであり、「ＰＬ同相（Piecewise Linear 同相）を前提とした一般化されたポアンカレ予想」や「微分可能同相 （Differentiable 同相）を前提とした一般化されたポアンカレ予想」ではありません。ちなみに、各前提条件での一般化されたポアンカレ予想について現在 わかっている事をまとめると、下表のようになっています（〇：予想の成立が証明済、×：予想の不成立が証明済、？：成立するか否かが不明、※：次元により 成立・不成立・不明のいずれか）。（**）

次元 位相同相 ＰＬ同相 微分可能同相
１ 〇 〇 〇
２ 〇 〇 〇
３ 〇 〇 〇
４ 〇 ？ ？
５ 〇 〇 〇
６ 〇 〇 〇
７ 〇 〇 ×
８以上 〇 〇 ※

（**） 参考書籍：　『宇宙が見える数学』　小笠英志 著　講談社ブルーバックス　2024年
　　　　参考資料：　Wikipedia　『Generalized Poincare conjecture』

トップへ戻る