ギーゼキング多様体 と レンズ空間
ギーゼキング多様体（Gieseking Manifold）は、正四面体の各面を右図のように貼り合わせることで得られる開３次元多様体です。
この多様体は、向き付け不可能な双曲３次元多様体です。
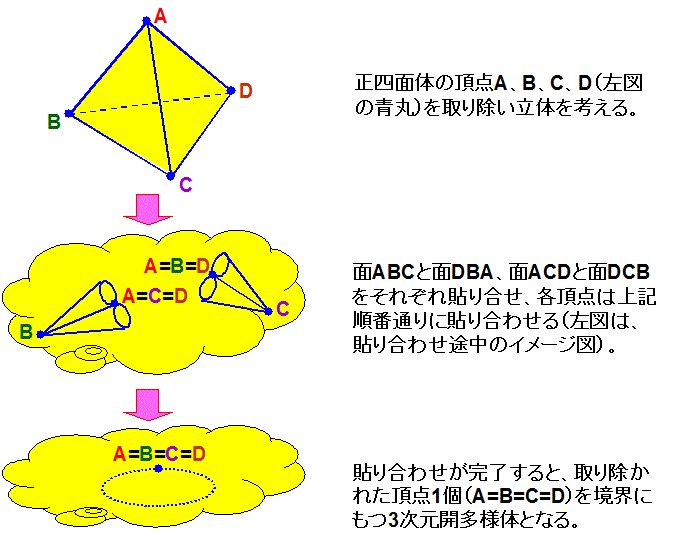
まず、右図（上）のように、正四面体の頂点A、B、C、D（図の青丸）を取り除いた立体を考えます。
つぎに、面ABCと面DBA、面ACDと面DCBをそれぞれ貼り合せますが、このとき、各頂点は記号順の通りに貼り合わせます。
すなわち、面ABCと面DBAの貼り合わせでは、AとD、BとB、CとAが重なるようにし、面ACDと面DCBの貼り合わせでは、AとD、CとC、
DとBが重なるようにします。なお、右図（中央）は、面ABCと面DBAを貼り合わせた状態と、面ACDと面DCBを貼り合せた状態を別々に
描いたもので、貼り合わせの途中を表すイメージ図です。
結果として、貼り合わせが完了すると、取り除かれた頂点1個（A=B=C=D）を境界にもつ3次元開多様体となり、ギーゼキング多様体
が完成します。そのイメージ図を、右図（下）に示します。
参考資料： ・Wikipedia 『ギーゼキング多様体』
前述のように、ギーゼキング多様体は向き付け不可能な多様体ですが、この向き付け不可能であることは、以下のようにして
確かめられます。
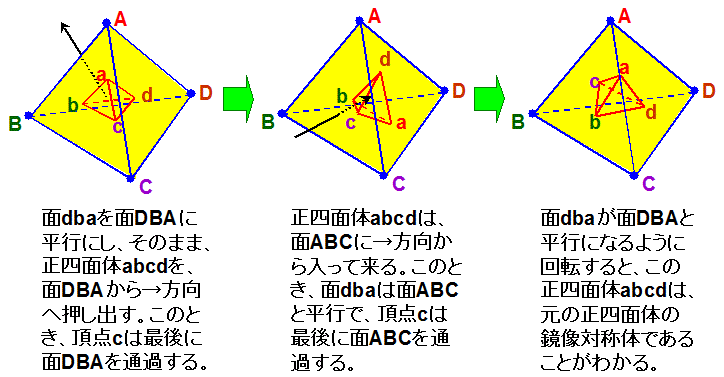
まず、下図（左）のように、ギーゼキング多様体の中に、ある正四面体abcdを配置します。なお、わかり易くするため、ここでは、
ギーゼキング多様体は正四面体ABCDの形で表しています。
下図（左）では、面dbaを面DBAに平行になるように正四面体abcdを配置し、その平行状態を維持しながら、正四面体abcdを、
面DBAから→方向へ押し出します。このとき、面dbaは、面DBAに対して平行のまま、面DBAを通過します。また、頂点cは最後に
面DBAを通過します。
すると、前述のように、ギーゼキング多様体では面DBAと面ABCが貼りあわされているので、下図（中央）のように、正四面体abcdは、
面ABCに→方向から入って来ます。このとき、面dbaは、面ABCに対して平行の状態を維持しながら、面ABCを通過します。また、
頂点cは最後に面ABCを通過します。
次に、下図（右）のように、面dbaが面DBAと平行になるように正四面体abcdを回転します。すると、この正四面体abcdは、
下図（左）にあった元の正四面体abcdの鏡像対称体となっていることがわかります。
すなわち、ギーゼキング多様体の中では、元の立体とその鏡像対称体は区別できないのです。したがって、ギーゼキング多様体は
向き付け不可能な多様体であることがわかります。
ところで、前述の正四面体の貼り合わせにおいて、ギーゼキング多様体の場合とは異なる貼り合わせ方をすると、
３次元球面が得られます。具体的に言うと、冒頭の図に示した正四面体ABCDにおいて、各頂点は
取り除かず、面ABCと面DBC、面CADと面BADをそれぞれ貼り合せる（各頂点は記号順の通りに貼り合わる）と、３次元球面となります。
なお、３次元球面は向き付け可能な３次元閉多様体ですが、この向き付け可能であることは、ギーゼキング多様体の場合における
上図と同様の図を用いて、正四面体abcdを移動させることにより確かめることができます。
また、冒頭の図に示した正四面体ABCDにおいて、各頂点は取り除かず、面ABCと面BCD、面CDAと面DABをそれぞれ貼り合せる（各頂点は
記号順の通りに貼り合わる）と、レンズ空間の一種で、L(4,1) と言う記号で表される多様体と
なります。なお、L(4,1) の基本群は位数４の巡回群となります。なぜなら、一般に、L(p,q) （※ p、q は整数）の基本群は、p≠0 のとき、
位数 p の巡回群となるからです。
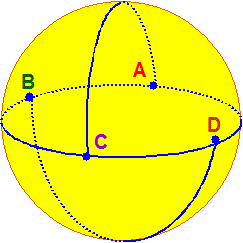
正四面体のこの様な貼り合わせにより L(4,1) が得られることは、次のようにして確かめられます。まず、右図のように、正四面体を
変形して球体にします。ただし、このとき、正四面体の各面は、４つの頂点 A、B、C、D が球の赤道（球の中心を通る平面と球面の
交線）上に来るようにします。すると、前述の貼り合わせは、赤道より上の半球上の面ABC、面CDAをそれぞれ π/2 回転して、赤道
より下の半球上の面BCD、面DABにそれぞれ貼り合わせることに相当します。すなわち、p＝4、q＝1 のとき、2qπ/p＝π/2 となるから、
この貼り合わせにより生じた３次元閉多様体はレンズ空間 L(4,1) であるとわかります（→ レンズ
空間についての記述と図 参照）。
なお、右図から容易にわかるように、回転角を変えることにより、別のレンズ空間も得られます。すなわち、赤道より上の半球上の
面ABC、面CDAをそれぞれ 3π/2 回転して、赤道より下の半球上の面DAB、面BCDにそれぞれ貼り合わせると、
p＝4、q＝3 → 2qπ/p＝3π/2 であるから、レンズ空間 L(4,3) となります。
ただし、上記の L(4,1) と L(4,3) は、p＝4 、q＝1 、q'＝3 、k＝1 → qq'＝3＝4−1＝kp−1 であるから、位相同形となります
（→ レンズ空間についての記述と図 参照）。
また、このレンズ空間 L(4,1)（＝L(4,3)）は向き付け可能な３次元閉多様体ですが、向き付け可能であることは、前述の様に
小さい正四面体を移動させて確かめることができます。さらに、一般に、レンズ空間 L(p,q) （※ p、q は整数）は、向き付け可能な
多様体となります。
ところで、レンズ空間は、立方体（正六面体）の各面を次のようにして貼り合わせることでも得られます。
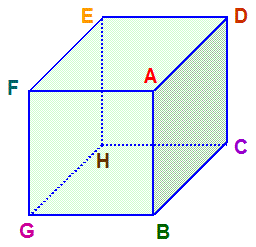
はじめに、右図のような立方体ABCDEFGHを考えます。
すると、面ABCDと面HCDE、面ADEFと面HEFG、面AFGBと面HGBCをそれぞれ貼り合せる
（各頂点は記号順の通りに貼り合わる）と、レンズ空間 L(6,1) が得られます。
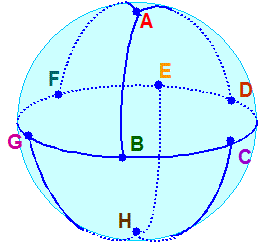立方体のこの様な貼り合わせにより L(6,1) が得られることは、正四面体のときと同様の方法で確認できます。まず、右図のように、
立方体を変形して球体にします。ただし、このとき、立方体の各面は、６つの頂点 B、C、D、E、F、G が球の赤道（球の中心を通る
平面と球面の交線）上の等間隔の点、２つの頂点 A、H が北極点と南極点（球の中心を通り赤道面に垂直な直線と球面の交点）に
来るようにします。すると、前述の貼り合わせは、赤道より上の半球上の面ABCD、面ADEF、面AFGBをそれぞれ π/3 回転して、赤道
より下の半球上の面HCDE、面HEFG、面HGBCにそれぞれ貼り合わせることに相当します。すなわち、p＝6、q＝1 のとき、2qπ/p＝π/3 と
なるから、この貼り合わせにより生じた３次元閉多様体はレンズ空間 L(6,1) であるとわかります。
なお、右図から容易にわかるように、回転角を変えることにより、別のレンズ空間も得られます。すなわち、赤道より上の半球上の
面ABCD、面ADEF、面AFGBをそれぞれ π回転して、赤道より下の半球上の面HEFG、面HGBC、面HCDEにそれぞれ貼り合わせると、p＝2、
q＝1 → 2qπ/p＝π であるから、レンズ空間 L(2,1) （＝３次元実射影空間）となります。また、赤道より上の半球上の
面ABCD、面ADEF、面AFGBをそれぞれ 5π/3 回転して、赤道より下の半球上の面HGBC、面HCDE、面HEFGにそれぞれ貼り合わせると、
p＝6、q＝5 → 2qπ/p＝5π/3 であるから、レンズ空間 L(6,5) となります。
ただし、上記の L(6,1) 、L(2,1) 、L(6,5) のうち、L(6,1) と L(6,5) は、p＝6 、q＝1 、q'＝5 、k＝1 → qq'＝5＝6−1＝kp−1 で
あるから、位相同形となります。
一方、右上図の立方体ABCDEFGHにおいて、面ABCDと面AFED、面BGHCと面FGHE、面AFGBと面DEHCをそれぞれ貼り合せる（各頂点は
記号順の通りに貼り合わる）と、レンズ空間 L(0,1) （＝Ｓ2ＸＳ1 多様体）が得られます。なお、L(0,1) の
基本群は、Ｚ＝｛ 0, ±1, ±2, ±3, ・・・ ｝ ： 整数全体の加法群 となります。
また、以上の正四面体や立方体と同様に、正八面体、正十二面体、正二十面体のそれぞれについて、各面を適宜に貼り合わせることでも、
レンズ空間は実現できます。具体的には、正八面体からは L(1,0) （＝３次元球面）、L(4,1)（＝L(4,3)）、L(2,1) （＝３次元実射影
空間）、正十二面体や正二十面体からは L(10,1)（＝L(10,9)）、L(10,3)（＝L(10,7)）、L(2,1) （＝３次元実射影空間）と言った
レンズ空間がそれぞれ得られます。
なお、正十二面体において、各面の貼り合わせ方を変えると、レンズ空間とは異なる３次元多様体である
ポアンカレ球面やザイフェルトウェーバー多様体が
得られます。
