| 絞りとボケ(被写界深度.1) 華室 夷蔵 |
全体 |
|||||||||||||||||||
| 本ページ |
||||||||||||||||||||
| 筆者へのメール | ||||||||||||||||||||
| 2014年9月24日、改定しました。 別ページの被写界深度グラフをこのHPに挿入し、エアリーディスクの説明図と文章を変えました。 |
トップへ | |||||||||||||||||||
| カメラの絞りとボケの関係(被写界深度)について解説しています。 最近のレンズでは無くなってしまった被写界深度目盛りに代わる被写界深度グラフを作りました。 過焦点距離で共通化することによりズームレンズ数本分を1枚のグラフにまとめています。 絞り過ぎ時の回折効果によるボケ(小絞りボケ)も解説しています。 カメラの絞りとボケに関して (1)絞りを絞った(数値を大きくした)方が、ボケは小さくなる。 (2)絞りを絞り過ぎるとボケがおおきくなる。 (3)同じ絞りの場合、フィルムカメラに比べてデジカメの方がボケない。 (4)同じ絞りの場合、フィルムカメラと比較するとデジカメの方がボケが大きい などと言われています。 (1)と(2)、(3)と(4)はそれぞれ全く逆のことを言ってますが全てが正しいことを言ってます。 全く逆のことが正しいのはそれぞれ、観点・視点や比較条件が異なるためです。 これらについて説明します。 なお、(1),(3)のボケと(2)、(4)ののボケとは原因は異なるのですが、最近は(2)、(4)は小絞りボケと言われることも多くなっています。 (1)絞りを絞った(数値を大きくした)方が、ボケは小さくなる。 は写真A1〜写真A7をご覧ください。 |
||||||||||||||||||||
|
||||||||||||||||||||
| 絞りの数値が大きくなるにつれて、写真の上と下の花(夏椿)の部分はボケが小さくなっています。 厳密な意味で写真のピントが合っているのは下から2つ目の花だけで、上下の部分のピントは合っていませんがボケが小さいので特に写真A6,A7は全体にピントが合っているように見えます。 理論的な説明に入ります。 簡単な解説では、レンズは薄い1枚の凸レンズで表され、レンズから被写体までの距離と、レンズから撮像面(フィルムや撮像素子ある位置)までの距離はレンズの中心から測るようになっていますが、実際のレンズは複数枚の凸レンズ・凹レンズの組み合わせで構成されおり、単純にレンズ群の中央から測ることはできなくなっています。そこで距離を測る基準点を決め、被写体までの距離を測る基準点を第1主点、撮像面までの基準を第2主点といいます。第2主点は公称の焦点距離です。第1・第2主点は通常実際のレンズの最前面や最後面とは異なる仮想的な位置にあります。詳しくはレンズの部屋で解説しています。 |
||||||||||||||||||||
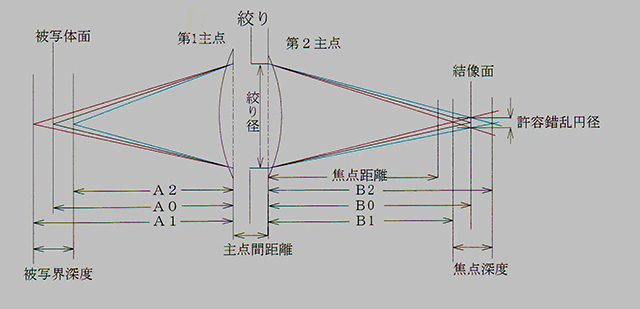
図1:結像図 |
レンズの基本式 1 1 1 −+−=− A B f A:レンズの第1主点から被写体までの距離 B:レンズの第2主点から結像面(フィルム,CMOSやCCD)までの距離 f:レンズの焦点距離 撮像倍率 B K=− A F値:絞り f F=− D D:絞りの直径 ※分母の絞りの穴が小さいほどF値は大きい |
|||||||||||||||||||
| 上の図1のように、A0にある被写体は撮像面B0にピントが合っていますが、A0より遠い被写体A1はB0の少し前のB1にピントが合い、B0の位置では少しボケています。A0より少し近いA2はB0より後ろのB2にピントが合ってB0では少しボケています。 絞りの数値を大きくすると、絞りの穴の直径は小さくなり、B0の位置でのA1やA2のボケが小さくなります。 絞りの数値(f値)を大きくすると穴の直径が小さくなるということがややこしく混乱する方がいらっしゃるようですが、雑巾を絞るとき力を入れると雑巾の直径は小さくなると覚えてください。2段分絞ると直径は半分になります。 ボケの大きさを錯乱円径と言いますが、これが小さいと、写真A6、写真A7の様にある範囲に入っている被写体の全部にピントが合っているように見えます。 ピントが合っているように見えるボケの大きさを許容錯乱円と言い、ピントが合っているように見えるまでの距離範囲(図の1のA1からA2まで)を被写界深度と言います。一般的には、35mmフィルムの場合で許容錯乱円の大きさは30ミクロン(約30分の1mm)とされています。 図1でA0を無限遠,、すなわち非常に遠方にピントを合わせたとき、結像面はレンズの焦点距離の位置になります。このとき、A2すなわち、ぎりぎりでピントが合ったように見える最も近い位置は焦点距離より少し後ろに焦点を結ぶので、結像面では少しボケますが、無限遠からA2までピントが合っているように見えます。このA2を過焦点距離と言います。逆に過焦点距離にピントを合わせると、無限遠にはぎりぎりでピントが合い、過焦点距離の半分の位置がピントが合う最も近い距離になります。 すなわち、過焦点距離の位置にピントを合わせると、無限遠は少しボケ、過焦点距離にピントが合い、過焦点距離の半分で少しぼけてはいるが、無限遠から過焦点距離の半分までピントが合ったように見える写真が撮れます。これをパンフォーカス撮影といいます。 過焦点距離Hは、レンズの焦点距離をf、絞りをF、許容錯乱円径をdとすると H=f2/(F*d) となります。 ここで、例えば、焦点距離と絞りの組み合わせに着目すると、 24mm/F2,28mm/F2.8,35mm/F4、50mm/F8、70mm/F16、100mm/F32 は大体同じ過焦点距離(この例では約10m)になります。すなわち焦点距離が2倍のときは絞りの数値を4倍にすると過焦点距離が等しくなります。 さらに、一眼レフの絞りは、通常数値の大きい方から32,22,16,11,8,5.6,4,2.8,2,1.4・・・のような数列になっており、dは前述のように30μmですが、これを概算で1/32mmとすると H=f2*(32/F)となって計算が楽になります。 すなわち絞りを32にすると、過焦点距離は、焦点距離の2乗、絞り16でその2倍、絞り22ではこれも概算で過焦点距離の1.5倍となり、計算が容易になります。 過焦点距離はマジックナンバー |
||||||||||||||||||||
|
||||||||||||||||||||
| 写真B−1は焦点距離24mmの単焦点レンズ、距離0.7m弱位で、絞り16のとき0.5m弱から1.5m程度まで、f=8なら57cm〜90cmまでが被写界深度であることが分かります。写真B−2は17−35mmのズームレンズですが、被写界深度目盛りは焦点距離17mmでのみ有効になっています。写真B−3は直進式ズームレンズで全ズーム範囲の被写界深度メモリが刻まれていましたが大きく重いレンズでした。 また、焦点距離を短くすると全長が長くなるズームレンズもあります。このようなレンズでは下図の写真B−3のような目盛が描けません。 |
||||||||||||||||||||
| 被写界深度は上記のように計算できますが、必要になる度に計算するのは面倒なのでグラフを作りました。 被写体までの距離を測る基準は前述のように第1主点から測るように作成してありますが、現実には第1主点の位置は公開されいないので、基準があいまいになります。しかしある程度離れた位置なら、主点位置は無視しても誤差は十分に小さいと考えられます。例えば数メートル遠方なら主点位置が不明であっても数センチから数10センチ位は目測の誤差に含まれると思います。そのため1m以上で使うようにグラフを作りました。 下図の上段はフルサイズ用、下段はAPSCサイズ用です。 |
||||||||||||||||||||
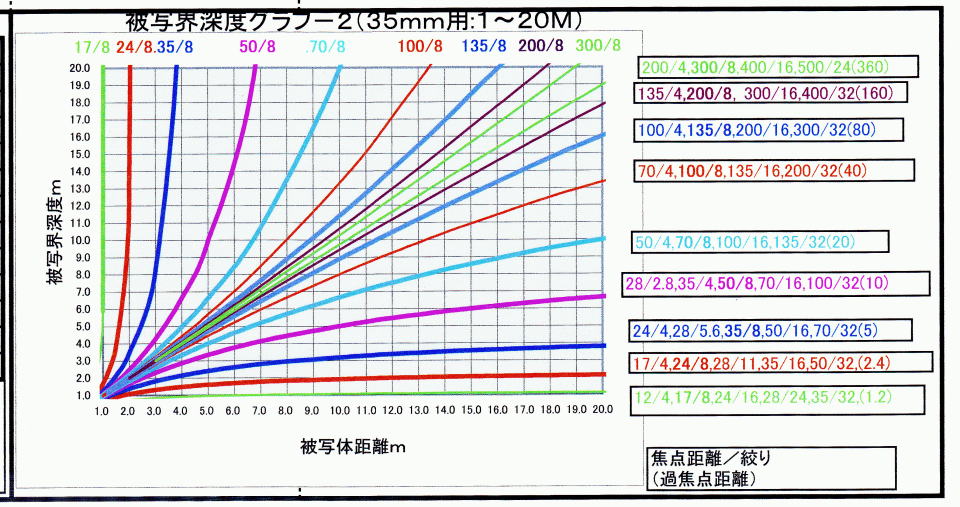 図2A フルサイズ用対数目盛(1m〜10m) |
||||||||||||||||||||
| 横軸は被写体までの距離。縦軸は被写界深度です。ともに基点はレンズの第1主点です。 上段はレンズの焦点距離、右は焦点距離とF値の組み合わせ、及び過焦点距離です。 |
||||||||||||||||||||
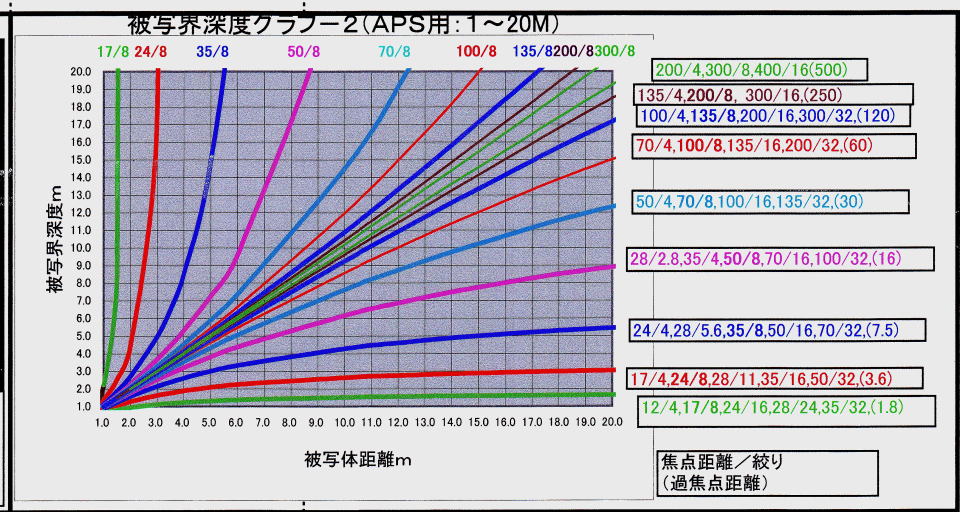 図2B APSCサイズ用対数目盛(1m〜10m) 横軸はレンズの主点から被写体までの距離。縦軸は被写界深度です。ともに基点はレンズの第1主点です。 上段はレンズの焦点距離、右は焦点距離とF値の組み合わせ、及び過焦点距離です。 |
||||||||||||||||||||
| 計算式には焦点距離が含まれていますが、個々の焦点距離毎に対応するのは非常に複雑で実用性が無いので、各過焦点距離に対応させて代表値(f=100mm)で計算しています。計算上は若干の誤差が含まれますが、距離の目測の誤差よりは小さく、まず問題はないと思っています。 過焦点距離が同じグループ(例えば35mm/F4,50mm/F8,70mm/F16,100mm/F32)でどの程度の違いができるかは 計算式でご確認ください。この誤差が大きいと思われる方は被写界深度グラフは使わないでください。 私はグラフを紙幣と同じ大きさにプリントして財布に入れておき必要なときに使っています。 実際のレンズの被写界深度に関しましては、例えば下記で公開されています。 http://www.tamron.co.jp/data/depth/index.htm 本グラフとの差をご確認ください。 実レンズでは、同じ焦点距離でもレンズが異なれば若干の差が出ています。これは、上記のタムロンのHPのデーターはカメラの基準位置から測定することになっており、レンズの第1主点位置が異なることが主な原因です。 グラフはレンズの第1主点からの距離で作成していますから、マクロ撮影や近傍の撮影など被写体距離が短い時は誤差が大きくなります。大まかな目安として1m以上で使っています。 今回はある程度離れた位置から撮影するために過焦点距離でまとめた被写界深度を紹介しました。マクロ・近傍の被写界深度は別の基準でまとめることが必要です。別途紹介する予定です。 次に、 (2)絞りを絞るとボケがおおきくなる。 については、写真C1〜C7を見てください。 |
||||||||||||||||||||
|
||||||||||||||||||||
|
理論的な説明 上の図1では、A点から出た光は全てa点に集まるように書いていますが、絞りの縁に当たった光は少し広がってa点以外にも当たるようになります。これを回折現象といい、回折現象によって画像の鮮鋭感が低下します。ピントずれによるボケとは原因は異なりますが最近は小絞りボケと言われることも多くわかりやすい言葉だと思います。 フィルムの時は、写真のプリントで大きく延ばすことが少なくこの現象自体は知られていましたが、初心者の間では大きくは問題になっていなかったのですが、デジタルカメラが普及して誰でもが簡単にA4〜A3までプリントで延ばしたり、ディスプレイで見る機会が増えたのでこの問題が取り上げられるようになりました。 |
||||||||||||||||||||
|
||||||||||||||||||||
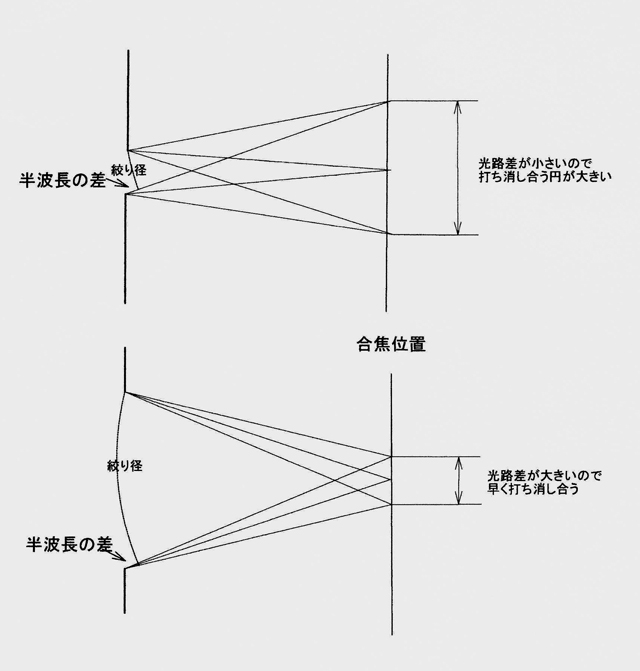
| 回折現象が発生するのは光が波動の性質を持っているためです。以下は正確さよりわかりやすさに重点を置いて概念的な解説です。 厳密な計算は三角関数の積分等複雑な理論になります。詳しく知りたい方は例えばこちらで知ることができます。 一点に集まる光の波動のずれ方(位相)によって光の強度が強くなったり、打ち消しあって弱くなったりします。 中心は、絞りの各周辺からの位置が全て等しいので、全ての位相が等しくなり最も明るくなります。焦点の極近くでは絞りの穴が大きくても小さくても、絞りの直径の上端で回折された光と下端で回折された光路のずれが小さいので図D2の中央の白い円になります。少し離れた点(図D1参照)で見ると絞りのの一端で回折された光と、反対の端で回折された光路のずれが大きくなります。絞りの穴が大きいほど光路差ずれも大きいのでボ図D2の最初の黒い早くできるようになり、中央の白い部分の直径が小さくなります。 更に離れた点でも絞りの両端で回折された光が1波長分ずれると再び強め合って、図D2の白い弱いリングが発生します。すなわち同心円状のボケを発生しますが通常は外側のリングは弱いので中央の白い円だけに着目すればOKです。 このボケをエアリーディスクといいます。 絞りをF、光の波長をλとすると、エアリーディスクの半径rは r=1.22λF λ:光の波長 となります。 絞りを絞ってF値を大きくすると、エアリーディスクも大きくなります。 また、F値は絞りから合焦位置までの距離を絞りの直径で割ったものですから、合焦点からみた画角は焦点距離に関係なく一定になることが主因でエアリーディスクの直径は、絞りの値だけで決まり、レンズの焦点距離には無関係です。 更に、回折効果で合焦点に向かう光が、それ以外に達することは逆に合焦点以外に向かう光が合焦点に達するはずです。例えば絞りを F=8からF=32まで絞ると、本来の光は絞り円の面積に比例して1/16になりますが、合焦点以外に向かう光が合焦点に達する成分は円周に比例しますから1/4になるに過ぎません。すなわち本来の画像信号は絞りの面積(2乗)に比例しますが、偽信号は絞りの円周(1乗)に比例し、信号と偽信号の比が低下します。この現象が画面のいたるところで発生します。これが絞りすぎるとエアリーディスク以外にコントラストが低下し、混色が発生する理由です。 小絞りボケは被写体のエッジ部のボケで、混色は被写体の平坦部のボケです。F=11位ではエッジ部のボケが目立ち始めますが、混色はまだ目立たず、F=22位で認識できるのだと思っています。 これは、概念的にはレンズのMTF特性で、30本/mmは解像度、10本/mmのコントラストに影響があるとされるのに似ており絞り過ぎによるボケは鮮鋭感とコントラストの双方に影響があるためです。 その他に、レンズの収差による画像の劣化も存在し、これはレンズの周縁部をいっぱいまで使う開放絞りよりは1〜2段絞った方が画質が良いといわれています。カメラ用ではなく顕微鏡用のレンズですが レンズの収差 をご参照ください。 (1)、(2)をまとめると、絞りを絞ると被写界深度が深くなりますが、必要以上に絞ると回折効果のためピントを合わせた位置での画像の鮮鋭感が劣化する。特に望遠系のレンズでは、被写界深度が浅いので、回折効果による劣化と被写界深度のボケとの優先度・バランスを考慮する必要がある。そのためには被写界深度の目安となるものが必要なので、被写界深度グラフがあると便利だと思います。ズームレンズの小型・軽量化に伴いレンズ自体に刻まれていた被写界深度目盛りがなくなったように、必須ではないですが、単焦点レンズには今でも刻まれているように全く無用ではなくあると良い便利グッズだと思います。 (3)同じ絞りの場合、デジカメの方がボケ難い。 これは、フィルムとデジカメの違いよりは、受光面サイズの違いです。フィルムカメラでも35mmフルサイズとAPSCサイズのフィルムでも同じことが言えます。 デジタルの場合は、撮像素子の前に付いているローパスフィルタの影響が皆無ではありませんが、ここで議論している被写界深度や回折効果による小絞りボケに比べて影響が小さいのでフルサイズの場合にはデジタルもフィルムも同じとしています。 フィルムカメラにはもっとサイズの大きいカメラもあり、デジタルもボツボツ大きいサイズが出始めています。 前述のように35mmフルサイズで許容錯乱円は30ミクロンでしたが、APSCサイズはプリントするときに35mmフルサイズより約1.5倍大きく引き伸ばされますから、許容錯乱円は20ミクロンになります。それによって35mm換算で同じ焦点距離と同じ絞りでも被写界深度が変わってきます。 被写界深度グラフの下段がAPS用になっています。これを参考にして、 例えばフルサイズの焦点距離50mmとAPSの焦点距離35mmで比べると
|
||||||||||||||||||||
| となって撮像素子サイズの小さいほうが被写界深度が深くなります。すなわちボケにくくなります。 フォーサーズや更に撮像素子の小さい多くのコンパクトデジカメでは更に焦点深度が深くパンフォーカスに近い写真になります。 |
||||||||||||||||||||
| (4)同じ絞りの場合、デジカメの方が(小絞り)ボケが大きい 前述のように、絞りのF値が同じならエアリーディスクの径は同じです。すなわち35フルサイズでもAPSCサイズでもF値が同じなら撮影素子上のエアリーのボケは同じです。プリントすると(パソコンのモニターで見る場合でも)APSCサイズは35mmに比べて約1.5倍大きく引き伸ばされるので撮像素子の小さい方が合焦点での小絞りボケ(エアリーディスク)が見かけ上大きくなります。すなわち焦点の合っている被写体においては撮像素子の小さい方がボケが大きくなります。この観点からは、コンパクトデジカメや携帯電話のカメラの画素数はエアリーボケの限界を超えており意味のない競争になっていますが素人にわかりやすい「画素数」は営業政策上は重要なようです。 (3)、(4)を、まとめると撮像素子の小さいデジカメでは35mmフルサイズに換算した焦点距離と絞りが同じでも、被写界深度が深くなるのでボケが小さくなるが、ピントをあわせた位置での回折効果の影響は受けやすくなることになります。 |
||||||||||||||||||||
| 補足その他 | ||||||||||||||||||||
| (1)許容錯乱円(ボケの許容値)の根拠:後付の理屈のようですが以下の説が受け入れやすいと思います。 ※1)視力検査”C”のリングの切れ目が視力1.0用で3mのとき約1mm 2)写真は対角線の距離離れて見ると仮定すると、35mmフィルムで対角線の長さは43mmですから、許容されるボケは、14μmになりますが 3A)視力検査は凝視するが、写真は全体を鑑賞する。 3B)視力検査はコントラスト100%だが、写真のコントラストはもっと低い ⇒約2倍として30μmまで許容とするとします。 一方で、2つの点が分離して識別できるためにはエアリーディスクの直径分だけ離れていることが必要になりますが前述の式から エアリーディスクの直径は D=2.44λf となってλ=0.5μm(緑の波長)とすると、 f=11の時に、D=13μmになりますから主役となる被写体を意識して凝視する場合には、f=11が限界で、視力の良い方や赤っぽく長波長が多いときにはf=8でもよく見れば劣化がわかることになります。 |
||||||||||||||||||||
| (2)3分の1の距離に合わせればよいのだが・・・・・、 被写界深度は手前に狭く奥側が広くなっています。これを拡大解釈して写したい範囲の3分の1の所にピントを合わせればバッチリだとするネットや雑誌の記事をたまに見かけそれを信じている方もいます。 例えば被写界深度グラフで、50mm/f8で4m、APS用の場合35mm/f8で3m位の所をご覧ください。確かに手前と奥の比は約1:2になっています。スナップ写真で2〜5m付近の物をf8で撮るときには、写したい範囲の3分の1の所にピントを合わせればほぼ全体にピントが合います。これを覚えておくと便利です。 ただし、常にこの比で良いのではないことも忘れないでください。 被写界深度グラフでわかるように近距離では被写界深度の幅は1:2より大きく、遠方では1:2より小さくなります 雑誌やネットの記事を書くときにはこのような条件付であることを同時に書いておいて欲しいものです。 (3)ローパスフィルターの塵 写真画像のボケとは異なりますが、デジタル一眼ではローパスフィルターの塵が写真に写りこむことが問題になります。多くのデジタル一眼には塵除去の機能もありますが完全ではないようです。 絞りを絞って開口を小さくすると塵の影も小さく濃く写りこむようになります。絞りを開いた方が影が大きく薄くなって目立ちにくくなので、撮影前に塵のチェックをするときは絞りを最大に絞って白い紙などを撮影すると分かり易くなります。 |
||||||||||||||||||||
| 最後までお読みいただきありがとうございました。 下の表は、このホームページの他のテーマです。
|
||||||||||||||||||||