トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは幻想である。
分子結合 ( CH4、H2O ) のページに戻る。
最初に 下記のプログラム中の ボーア模型のメタン (CH4) の計算手法について説明する。
この JAVA プログラムは ほぼすべてのブラウザで動くと思われる。
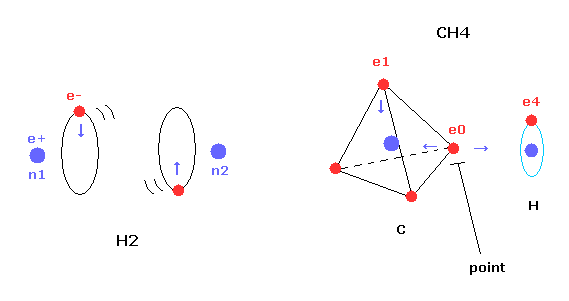
(Fig.1) CH4 における 横方向のでっぱり。

このページでは、 ボーア軌道を用いて 水素分子 (H2 を表すのに成功した。)
また 核間距離が実験値 (= 7414 MM ) のとき、H2 の結合エネルギーが最大になることを示した。
ここでは 新しい単位 1 MM = 1 × 10-14 meter を用いた。
しかし 単純な水素分子と異なり、メタン (CH4) の炭素原子は 4つの 正四面体状に分布した価電子を持つ。
そのため 炭素の1つの電子を 水素の電子軌道と平行になるようにしても、4つの中の別の電子が 必ず水素原子のほうに 突き出てしまう。
この突き出た炭素の電子は 水素原子の原子核を強く引きつけて そのポテンシャルエネルギーを低くする。
また この突き出た電子は 分子構造の不安定性を決定する際の重要な鍵となることを 後で示す。
(Fig.2) コンピュータープログラムの CH4 の構造。
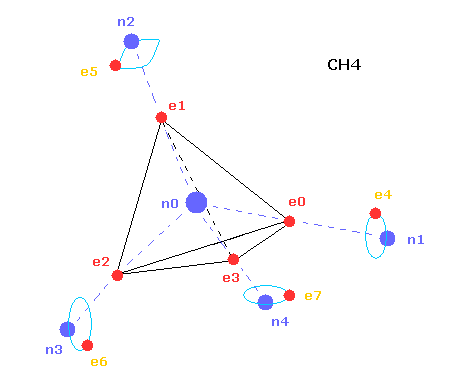
上記のコンピュータープログラムでは、Fig.2 のメタン模型を用いた。
炭素原子の4つの価電子 ( e0, e1, e2, e3 ) が 正四面体状に分布している。
また 4つの水素原子の原子核も正四面体状に分布している。
Fig.2 に示したように、 炭素の電子 e0 と 水素の n1 原子核は 同じベクトル上にある。
( 同様に e1-n2、 e2-n3、 e3-n4 も それぞれ同一のベクトル上にある。 )
(Fig.3) CH4 (= x-z 平面 ) の断面。
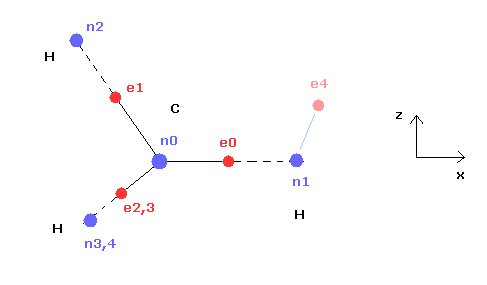
Fig.3 は Fig.2 の断面 ( x- z 平面 ) である。
上記のプログラムでは、テキストボックス上の 電子 e0 と e4 の座標のみ変更できる。
( e0 の x 座標と、 e4 の x、 z 座標のみ変更できる。)
テキストボックス上の e0 と e4 の入力座標に基づいて 残りの炭素の電子 ( e1-e3 ) と 水素の電子 ( e5-e7 ) が 自動的に正四面体状に配置される。
つまり 電子 1、2、3 ( と H の原子核 n2、3、4 ) の x 座標は 必ず同じになっている。
( このプログラムは 画面のスペースの都合上 テキストボックスだけで 絵は示していない。)
(Fig.4) プログラム実行直後の画面。
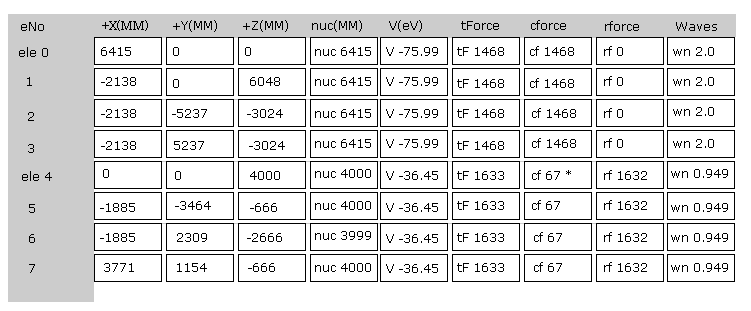
Fig.4 は JAVA プログラムを実行直後の 画面上の表示の上部分である。
ele 0, 1, 2, 3 は 炭素原子に属する電子である。
+X(MM), +Y(MM), +Z(MM) は 各電子の それが属する原子核に対する 相対的な座標である。
( ele 0-3 は 炭素の原子核 n0、 ele4 は H の原子核 n1、 ele5 は n2、 ele6 は n3、 ele7 は n4 に属する。 )
"nuc" は 各電子と それが属する原子核間の距離である。
ここでは 新しい単位 1 MM = 1 × 10-14 meter が使用されている。
"V(eV)" 各電子の位置エネルギーである。
"tForce" は 各電子に作用する トータルの力である。
"cforce" は 各電子に作用する力の 中心 (= C 原子核 ) 方向の力である。
"rforce" は 各電子 ( e4-e7 ) に作用する力の 各 C - H 原子核ライン方向 (= 垂直な ) への力の成分である。
"Waves" は 1軌道に含まれるドブロイ波の数である。
(Fig.5) Force = 1000.
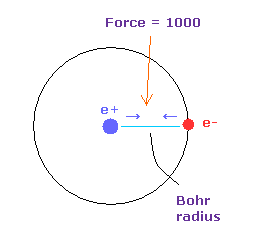
Fig.4 においては 水素原子の基底状態における 電子と原子核間に働く力の強さを "1000" としている。
そのため 電子と +e の原子核間の距離が ボーア半径のとき、その力が 1000 になる。
例えば、力 1468 は 水素原子の基底状態のときの力の 1.468 倍である。
各運動エネルギー (T) から 各ドブロイ波長を計算する。
ここでは ビリアル定理 ( -1/2V = T ) を使用している。
( "V" は ポテンシャルエネルギーである。 )
原子 (= 単一原子核 ) や H2 分子などの場合は それらの計算はシンプルである。
しかし 分子が 2つ以上で かつ 非対称的な 多電子を持つときは、少し注意する必要がある。
(Fig.6) O-H 結合と 各ポテンシャルエネルギー。
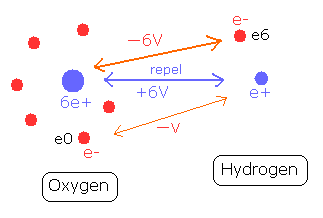
Fig.6 は 水分子の O-H 結合を示している。
水素の原子核 (e+) が 酸素原子の 6つ電子に引きつけられている。
水素原子核と 酸素の1つの電子 (e0) 間のポテンシャルは -V である。
一方で、酸素原子核は 水素原子の たった1つの電子 (e6) に引きつけられている。
そのため 酸素原子核と 水素の電子 (e6) のポテンシャルエネルギーは -6V となり、この結合力は 上のケースの 6倍も強い。
(Fig.7) 引力による V は 反発力による V でキャンセルされる。
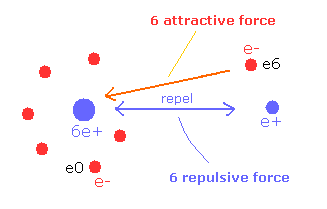
つまり e6 は 2つの反発する原子核を結合するのに 多くの仕事をすることになり、e6 のポテンシャルエネルギーを高くする。
( つまり 負のポテンシャルエネルギー -6V が 原子核間の +6V でほとんどキャンセルされることになる。)
この事実を考慮して、プログラムでは 電子-電子間、電子-原子核間のポテンシャルエネルギーを計算した後、正の原子核間 のポテンシャルエネルギーを 各電子に分配している。
例えば、この反発するポテンシャルエネルギーが +6V のとき、分配比は e6 と e0 で6:1 (= -6V: -V ) になる。
酸素は 6つの電子 e0-e5 を持つため、 +6V × 6/(1x6 +6) = +6V / 2 = +3V が e6 に分配され、 +6V × 1/(1x6+6)= +6V / 12= +3V / 6 が e0 に分配される。
( つまり ほぼ同じ +3V の反発ポテンシャルエネルギーが O-H 結合の各サイドに分配される。 )
上のプログラムでは、各電子と 他の原子核間とのポテンシャルエネルギー V (= rhp[el][6] ) を計算して、その rhp[el][6] の大きさに比例させて 原子核間の反発ポテンシャルエネルギー (= pota ) の値を 各電子に分配している。
各運動エネルギーから 各電子の速度 (= v ) と ドブロイ波長 (= h/mv ) を得ることができる。
(Eq.1) 全力 F = 遠心力。
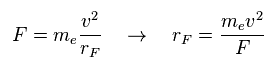
プログラムでは、各電子に作用する力の x、y、z 成分を計算する。
( rhp[el][0, 1, 2] = 力の x、 y、 z 成分。 )
ここでは それら力 F を 遠心力として扱う。
Eq.1 の関係式から ( 近似的な ) 回転半径 (= rF ) を得ることできる。
(Eq.2) 1軌道のドブロイ波。
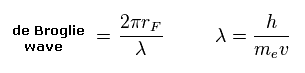
ドブロイの関係式 ( λ = h/mv ) を用いて、1軌道 (= 2πrF ) に含まれるドブロイ波の数を計算する。
炭素の外殻電子 e0-e3 のドブロイ波は "2"、水素の電子 e4-e7 のドブロイ波は "1" に近くなるべきである。
(Fig.8) 炭素の "有効" 中心電荷 = +Ze
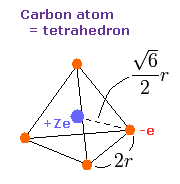
このページに示したように、炭素の 1s 電子の半径は 約 930 MM (= 0.0930 × 10-10 meter ) である。
2つの内殻の 1s 電子が 炭素原子核 +6e から少し離れていることを考慮すれば、4つの外殻の電子の 中心電荷 Z は +4e (= +6e - 2e ) よりも少し大きくなると考えるのが自然である。
Fig.8 では、正四面体の一辺の長さを 2r とする。
( Fig.8 の 4つの頂点は 炭素の4つの外殻電子を表している。)
4つの価電子の全エネルギー (E) は、-148.024 eV なので、ビリアル定理を用いて この位置エネルギー (V) は、2 × -148.024 = -296.048 eV となる。
Fig.8 の模型を使って、電子ー核、 電子ー電子の間の電位を計算していくと、全位置エネルギー V ( 単位 eV --> J ) は次のように示せる。
炭素のドブロイ波を計算する サンプル JAVA プログラム。
このプログラムでは 中心の正電荷 Z ( ほぼ 4.0 ) を入力した後、ポテンシャルエネルギー V、力、1軌道に含まれるドブロイ波を ビリアル定理 ( T = -E = -1/2 V ) や Eq.3 - Eq.7 の式を用いて計算する。
画面上には 回転半径 (MM) と 1軌道内のドブロイ波の数が 表示される。
(Eq.3)
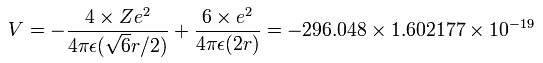
また、ビリアル定理より 4つの電子の全運動エネルギー (T) は、148.024 (eV) である。
(Eq.4)
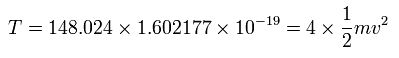
また、Fig.8 より、電子1つにはたらくクーロン力の合計 (F) は(核方向の力になるが)、次のようになる。
(Eq.5)
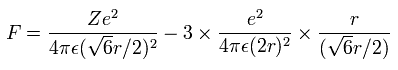
上の式の T 中の速度 (v) と、力 F の値を用いて、遠心力がこの力 (F) に等しいと仮定する。
(Eq.6)
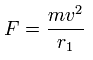
この r1 は、この関係式で初めて登場する 仮の半径である。
この r1 を用いて、次に示すように、1軌道に含まれる ド・ブロイ波の数 (wn) を計算することができる。
(Eq.7)
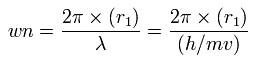
中心電荷 Z が +4.0 のとき、この wn は 1.87 (ほぼ 1.9) で 回転半径は 約 6000 MM となる。
また、Z = +4.22 のとき、この wn は、ちょうど 2.00 で、回転半径は 約 6400 MM になる。
炭素の4つの価電子を視覚化する サンプル JAVA プログラム。( 中心電荷 +4.22 )
実際に、上記のプログラムを実行して スクロールバーの中から "1.0" もしくは "2.0" をドブロイ波をして選択して "orbit" ボタンをクリックすると、Z = 4.22 のとき、1軌道が ちょうど 2.0 ドブロイ波長で、その回転半径 (= nuc ) が 約 6400 MM (= 0.6400 × 10-10 meter ) であることが分かる。
このページも参照のこと。
よって ここでは この 4.22 の値を 炭素の中心電荷として使用する (= プログラム内の "den" )。
(Fig.9) C-H 結合のドブロイ波。
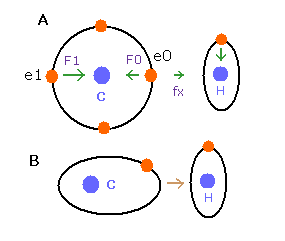
Fig.9A の e0 や e1 では、上のド・ブロイ波の計算方法を使うことはできない。
酸素 (O) の電子 0 (e0) では、水素原子核からの反対方向の引力 (fx) のため、Fig.9A に示すように 力 F0 は、電子1の力 F1 よりも弱くなる。
つまり、Eq.1 では、e0 の”仮の”半径 r1 は e1 に比べて長く なる。
これは、Eq.1, Eq.2 の計算方法を使うと、e1 (< 2.0) よりもより多くのド・ブロイ波 (> 2.0) が e0 軌道に含まれてしまう。
しかし、もし、1つのみの電子軌道に注目すると (Fig.9B)、ド・ブロイ波の数 ( = 2.0 ) はその軌道の位置や形を変化させることで維持される。
(正の電荷の水素原子核は、この電子軌道を少し平行移動させ、またそれを楕円形に変化させる。)
つまり、C-H 結合の炭素の電子の 1軌道のドブロイ波を計算するとき、近似的に 炭素内のみにおける力とエネルギーを考慮することにする。
( このプログラムでは teqq[el][3] が 炭素原子内の 各ポテンシャル V を意味している。)
(Fig.10) C-H 結合における各力。
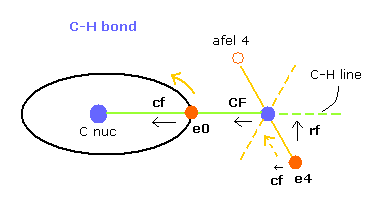
このプログラムでは "cf" は 各電子に作用する力の C 原子核方向への成分である。
"rf" は 電子 4-7 に作用する力の 各 C-H ライン方向に向かう成分である。
"afel 4" は 力の方向へ移動した後の 電子の位置の意味である。
( つまり 各電子は この場所のあたりを横方向に振動している。 )
電子軌道が ある地点で安定になるためには、この e4 の "cf" は 正になり afel 4 の "cf" は 負になる必要がある。
そして それらの絶対値は 安定のためには ほぼ同じにならなければならない。
( これは 安定な分子結合における 重要な点の1つである。)
"CF" は 各水素原子核に作用する力の C 原子核方向への力である。
つまり これら CF と cf が 正の値のとき、これらの粒子は C 原子核方向へ引きつけられていることになる。
(Fig.11) "afel 4" の位置。
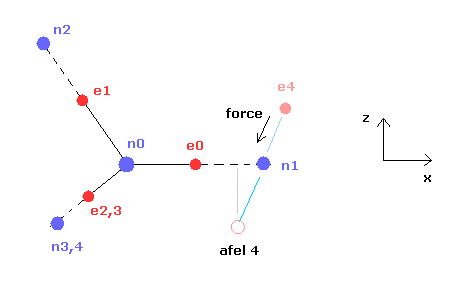
"afel 4" の x 座標を計算するとき、 "cf" の "rf" に対する力の比を用いる。
プログラムでは 力の "cf" 成分は rhp[el][4]、 "rf" 成分は rhp[el][5] で表している。
また afel 4 の z (と y ) 座標は 元の e4 に等しいとしてある。
(Fig.12) 平均の位置?

Fig.12 の分布を用いて 各粒子の力とドブロイ波を計算しようとするとき、4つの外殻電子と水素原子核が 平均的な値以上に 互いに強く引きつけられる。
( この標準的な分布のときの各座標は プログラム中で hpr[el][0-2] と表してある。 )
炭素の外殻電子軌道の半径は 約 6400 MM であり、これは 水素原子のボーア半径 5292 MM とほぼ同じである。
しかし 炭素の外殻電子軌道は 2ドブロイ波長であり、これは 水素原子の電子の 約 2倍の速さである。
そのため 水素原子との相互作用を考慮するとき、炭素原子に関して平均の分布を考える必要がある。
(Fig.13) 炭素原子の外殻電子の平均分布。
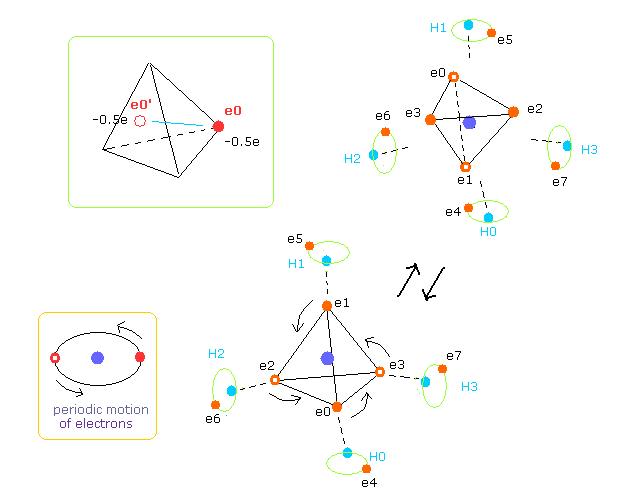
Fig.13 に示すように、炭素の 4つの外殻電子は ほぼ楕円軌道である。
そのため 各電子の逆方向の位置が 平均値をとる際に重要になる。
実際に ビリアル定理は 無限の時間周期に関する 平均値に等しい。
プログラムでは、炭素原子核に対する 電子 e0-e3 の逆の位置座標を計算する。
( この座標変数は hpr3[el][0,1,2] = hpr3[el][x,y,z] = -hpr[el][x,y,z] である。 )
そのため 速いスピードで動いている 炭素の4つの外殻電子は 半分の電荷を持つ 8つの電子を考えることができる ( -1.0e → -0.5e, -0.5e × 8 = -4e )。
( もちろん、電子 0-3 同士の反発力を計算するときは 元の4つの価電子のままで計算しないと、値が高くなりすぎてしまうので注意。)
"4-averwave" ( もしくは "0-averwave" ) は 元の ele4 と afel-4 のときの e4 ( もしくは e0 ) の平均したドブロイ波である。
これらのドブロイ波が ele4 で 1.0 ( ele 0 で 2.0 ) 近い値を得る座標を探す。
C-H 結合長を選んで "C-H ボタン" をクリックすると、メタンの C-H 長が変化する。
( C-H 結合長の実験値は 10900 MM である。)
"aCF" と "tV after" は、電子 4-7 の位置が afel 4-7 の時の H 原子核に作用する力と total V である。
このセクションでは 下のプログラムについて説明する。
( 基本的な計算手法に関しては 上のセクションも参照のこと。 )
違いは H2O は CH4 よりも非対称的な構造をしていることである。
そのため 酸素の電子 0-5 は 正八面体の構造を保てないということである。
(Fig.14) O-H 結合における "正八面体" 構造変化。
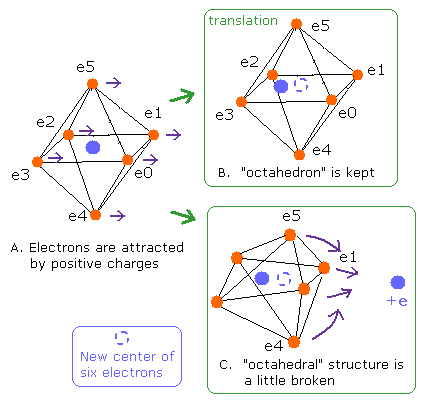
プログラム中では 酸素の電子 0-5 の 中心座標を noxx[0-2] として計算してだす。
酸素の中心電荷 ( den = + 6.273、後で説明するが ) は この中心位置にあるとして 酸素原子内でのみの 位置エネルギー、力 を用いて ele0-5 のドブロイ波をだす。
"O nuc FX, FY, FZ" は 酸素原子核に作用する力の成分である。
H0 (もしくは H1 ) の "On" と "Hn" は H0 ( もしくは H1 ) 原子核に作用する力の成分である。
( "On" は O 原子核方向 "Hn" は 他の H 原子核方向の力である。 )
"0-averwave" 電子 0-5 の 1軌道のドブロイ波の平均値である。
"6-averwave" は 電子 6 と 力に従って動いた後の 電子 6 のドブロイ波の平均値である ( Fig.10 も参照のこと )。
(Fig.15) 酸素原子の価電子。
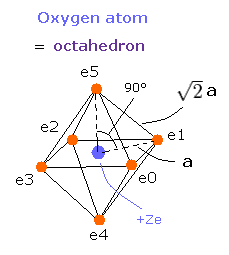
Fig.15 では、電子と中心の正電荷の距離を a とする。
ビリアル定理によれば、”平均の”全位置エネルギー (V) と運動エネルギー (T) は次の関係にある。
< V > = -2 × < T > , E = V + T
6つの価電子の全エネルギー (E) は、-433.103 eV なので、この位置エネルギー (V) は、2 × -433.103 = -866.206 eV となる。
Fig.15 の模型を使って、電子ー核、 電子ー電子の間の電位を計算していくと、全ポテンシャルエネルギー V ( 単位 eV --> J ) は次のように示せる。
(Eq.8)
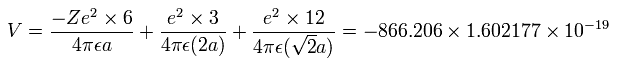
また、6つの電子の全運動エネルギー (T) は、ビリアル定理により 433.103 (eV) である。
(Eq.9)
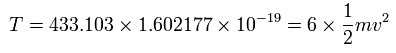
また、Fig.15 より、電子1つにはたらくクーロン力の合計 (F) は(核方向の力になるが)、次のようになる。
(Eq.10)
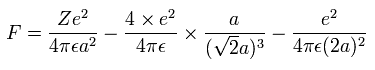
上の式の T 中の速度 (v) と、力 F の値を用いて、遠心力がこの力 (F) に等しいと仮定する。
(Eq.11)
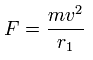
この r1 は、この関係式で初めて登場する 仮の半径である。
この r1 を用いて、次に示すように、1軌道に含まれる ド・ブロイ波の数 (wn) を計算することができる。
(Eq.12)
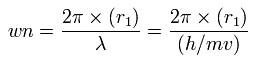
中心電荷 Z が +6.0 のとき、この wn は 1.88 (ほぼ 1.9) となる。
また、Z = +6.273 のとき、この wn は、ちょうど 2.00 になる。
この場合 2s 電子の回転半径は 約 4596 MM となる。
( ここでは 1 MM = 10-14 meter の新しい単位を使用している。)
O6+ と O5+ のページ で示されたように、2つの 1S 電子と核の間の距離は、約700 MM である。
つまり、この結果 ( 平均距離が 4596 MM) は、6つの外殻の電子が内殻の電子にぶつからず、安全に運動できることを示している。
また 700 MM の距離 原子核から離れているため 中心電荷は +6e (= +8e -2e ) よりも少し大きくなる。
例えば、水分子 (H2O) の O-H 結合長は、9584 MM である。つまり、この計算値 4596 MM はだいたい妥当な値と考えられる。

2013/3/9 updated This site is link free.