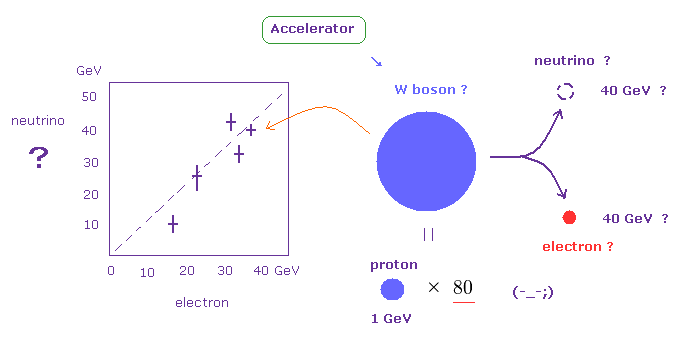
トップページ (2電子原子も含む正確な新ボーア模型)
特殊相対論は間違っている。
標準模型は間違っている。
役に立たない量子化学の原理。
(Fig.1) 加速器内の W ボソンと β崩壊の W ボソン ? とは まったくの別物。
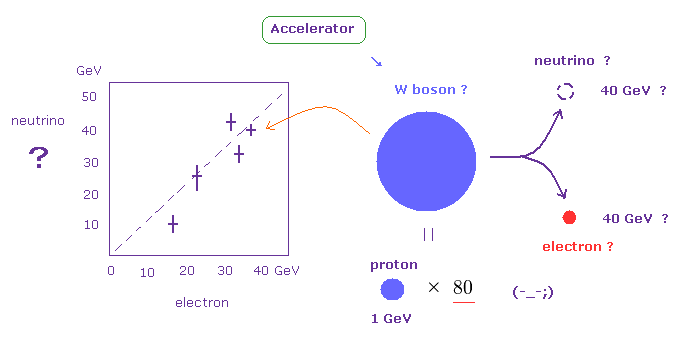
最初に、QCD の基礎となっている 非現実的な標準模型に触れなければならない。
W ( ウィーク ) ボソンは 高エネルギー加速器内での衝突によって 生じるとされている。
非実在的な W ボソンは 直接は 観測できない。
そのため 電子やニュートリノなどの最終生成物 (= 約 40 GeV のエネルギー ) を検出することによって 仮想の W ボソンの質量を推定しているにすぎない。
重要な点は、このページに示したように、肝心なニュートリノを加速器内で測定することができない。
この見えないニュートリノの存在を 最終産物のエネルギーの消失 (= 偏り ) などから 推定するしかないのである。
(Fig.2) β崩壊 では 全エネルギー ( W ボソンの ) の保存則が破れている。 ← 非実在的な粒子。
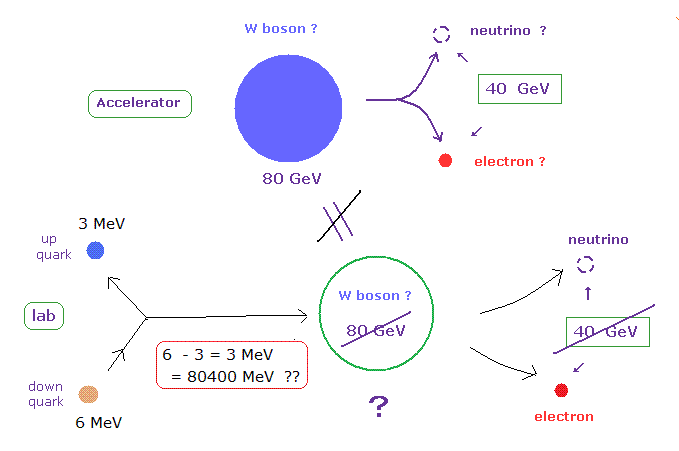
この 陽子の 80 倍もの 非常に重い W ボソン (= 80 GeV ) の質量は 高エネルギーの加速器でのデータを基に算出したものである。
つまり 加速器内での この W ボソンは 実験室内でのものをは まったくの 別物なのである。
通常の β 崩壊では、中性子内の ダウンクォーク が 負電荷の W ボソンを放出して 陽子内の アップクォークに変化するとされている。
しかし これら ダウンとアップクォーク間の質量エネルギーの違いは たったの 3 MeV であり、これは W ボソンの質量 (= 80 GeV = 80000 MeV ) よりも 比較にならないほど小さい。
つまり β崩壊の W ボソンが 高エネルギー加速器でのそれを等しいとすると、エネルギー保存則という 物理の基本的性質が 完全に破れていることになる。
これはつまり W ボソンとは 非常に非現実的な粒子なのである。
(Fig.3) 非現実的な Z ボソンは リアルなのか ? → 単なる電磁気力 ?

加速器内の 90 GeV 近くの共鳴点が Z ボソンの存在の証しだと 彼らは主張している。
重要な点は 中性の Z ボソンは 通常の電磁気力と 区別することができないのである。
なぜなら 光子 (= A ) も 同じく 中性だからである。
つまり 加速器内の Z ボソン関連の事象は 実際は 単純なクーロン散乱の1種であった可能性もあるのである。
(Fig.4) Z と W ボソンは 実は 同じもの ??

Z ボソンの質量 90 GeV は W ボソンの質量 81 GeV と非常に 近い。
つまり 最終産物であるレプトン (= 電子など ) は Z と W ボソンの両者において 約 40 GeV ほどのエネルギーを持つことになる。
W ボソンの最終産物の半分である ニュートリノが検出できないことを考慮すれば、実は 私達は Z と W ボソンの崩壊において 単に 同じ現象を 違った視点から見ていた可能性も十分にあるわけである。
( つまり 加速器内の "仮想の" 粒子 Z と W ボソンは 同一のものであった可能性がある。 )
(Fig.5) 対称性の破れ = クォーク・グルーオンの凝縮 ??

原子核質量の 98 % が カイラル対称性の破れによって生じ、 その たった 2 % が ヒッグス機構によって生じるとされている。
それなら このカイラル対称性の破れとは いったい何なのだろうか?
残念ながら、Fig.5 に示すように この カイラル対称性には まったく 物理的な イメージが ない と言っていい。
( これらは 単に 数学上の記号にすぎない。 )
物理的には、この QCD の質量は 陽子内の ( 海 ) クォーク と グルーオン間の 様々な相互作用によって生じるとされている。
しかしもちろん、これらの 想像上の状態を 実際に 視覚化することもできない。
(Fig.6) ヒッグスは "アップ"、 "ダウン" クォークに到達するために 常に陽子を破壊?

陽子の質量の ほとんどは QCD の機構によるもので ヒッグスは 関係ない。
陽子内の 非常に小さい "アップ" と "ダウン" クォークの質量は ヒッグス粒子によって与えられるとされている。
これはつまり 真空中のヒッグス粒子は 各クォークに達するために 頻繁に
陽子の殻を 破壊して 内部に侵入していることを意味しているのか?
もし このように 各陽子が ヒッグスによって 頻繁に "破壊されて" いるとすれば、非常に安定な 現実の陽子像と まったく異なる ものになってしまう。
つまり ヒッグスと QCD の組み合わせによる 質量獲得の機構は 非常に不自然極まりないのである。
一方で、ヒッグス粒子は 単一のトップクォークに 174000 MeV もの 巨大な質量を与えているとしている。
( QCD は この非常に重いトップクォークには 関与していないらしい。 非常に出来すぎの理論と思われないだろうか? )
(Fig.7) 強い力は 何も予測できない。
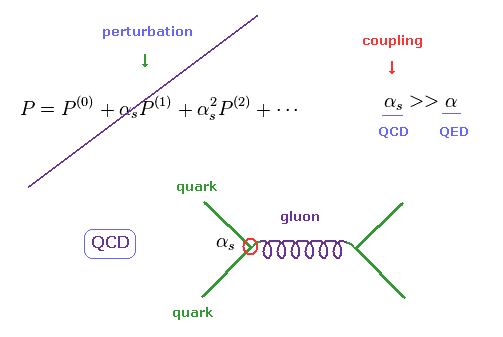
QED (= 量子電磁力学 ) の結合定数は 小さな 微細構造定数 α (= 1/137 ) に関係している。
つまり QED は 仮想の粒子と光子から生じる無限のループからの寄与の計算に 通常の摂動計算ができる。
彼らは QED は 正確な値を計算できると主張しているが、 このページに示したように、 彼らは 異常磁気モーメントや ラムシフトを得るのに 完全に間違った数学に頼っている。
一方で、強い力の 結合定数は エネルギーの値に応じて 劇的に変化する。
低エネルギーのもとでは、この結合定数が大きくなりすぎて、 クォークやグルーオン間の相互作用を計算することができなくなる。
そのため コンピューターを使った 何らかの近似的な数値計算に頼るしかないのが現状である。
これはつまり QCD は 実際の正確な値を与えることができないのである。
(Fig.8) QCD の格子ゲージ理論は ローレンツ変換不変でない。

数値計算をするには、有限の間隔 (= a ) を持つ 格子構造を用いる必要がある。
各クォークは 格子の 各頂点にあり、グルーオンは 2つのクォークを結びつける線 (= リンク ) で表される。
もちろん、この有限の間隔は 特殊相対論の ローレンツ対称性を 完全に 破っている。
( 例えば、この格子を 水平もしくは 斜め方向から眺めると 違って見えてしまう。 )
そのため まず ゼロでない "a" のときの値をいくつか数値計算し、それをつなげて a = 0 のときの 物理量を推定することになる。
これらの操作は ハドロン質量などの物理量の予測の際に 様々な誤差の要因になる。
(Fig.9) 虚数時間は リアルな世界と 等価ではない。

重要な点は QCD は 非現実的な 虚数時間 (= iτ ) に頼って 様々な物理量を出していることである。
つまり QCD は 実際の物理現象とは 根本的に 異なるものだということである。
例えば、陽子の質量の実験値は もちろん 現実的な時間 ( 虚数時間でなく ) の世界で 測定したものであることは言うまでもない。
QCD が なぜ 通常の時間の概念 (= t ) を使用できないのかというと、遷移確率 (= eiHt ) が 三角関数のように 振動して 一つに定まらないからである。
一方で、虚時間を用いると、その確率が 指数関数に変わり、振動することなく 収束するからである。
これはつまり この 虚数時間 (= QCD ) に立脚した 様々なハドロン質量は 現実の質量を 意味していないことになる。
(Fig.10) ファインマン経路積分 (= 無限の道筋 ) は リアルなのか?
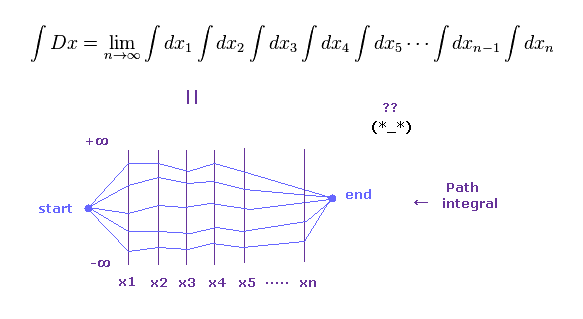
QCD の基本的な概念は ファインマンの経路積分に基づいており、各粒子は 最終状態になるのに 無限種類もの経路を 同時に通過するという奇妙なものである。
つまり これらの QCD の計算は たとえ スーパーコンピューターをたくさん同時に用いても 1つの計算値をだすのに 1年以上もの 長い時間を費やしてしまうのである。 恐ろしすぎる実態である。
経路積分の考えは 非現実的な多世界解釈に基づいている。
常識的な視点から考えて、小さな陽子の内部に 無限種類もの グルーオン、クォークを含んでいるという考えは 不自然極まりない。
( また もちろん、 "虚時間" も リアリティーがない。 )
つまり 現在の QCD の計算は まったくの時間の無駄遣いであり、多くの優秀な研究者たちの才能を 潰し続けていると言える。
(Fig.10') QCD の数値計算は 恐ろしく時間がかかる (= 1年以上 )。

QCD の格子ゲージ理論は ハドロンの近似的な質量しか得ることができない。
核の半径、磁気モーメント、ヘリシティー、クォークの運動量などでは 間違った値しか 出すことができない。
つまり QCD は すでに限界に達している学問と言える。
(Fig.11) 光子には 何の明確な実態がない。

彼らは エーテルを否定したため、電磁場を表現するのに (仮想)光子を導入する必要があった。
つまり 現在の場の量子論によれば、電場、磁場 それぞれが 光子という粒子で構成されていることになる。
さらに、光子は 電磁波 (= 光 ) に等しいと 彼らは主張している。
つまり 電磁波の単一光子は 電場の光子と 磁場の光子を合体させて生成されたのだろうか?
これはつまり 電磁波は 単一光子ではないということだろうか? ( 1 + 1 = "2" 光子 ? )
すると、現在の量子論は 最初から 自己矛盾を含んでいることになる。
(Fig.12) 光子 = 単なる 生成消滅演算子?

例え あなたがたが 場の量子論を勉強したとしても、光子の実態を知ることは不可能である。
現在の QED によれば、光子は 単なる数学上の生成 (= a† )、消滅 (= a ) 演算子 にすぎない。
これらの演算子は 非常に抽象的なため、具体的な”光子”の動きを表現することができない。
これらの演算子を用いて 光子を表現しようとすると、この単一光子は 真空中全体に生成される必要がある。
抽象的な演算子のために、光子の 特定の位置を指定することができない。
ベクトルポテンシャルの ゼロ成分 (= A0 ) は 電場ポテンシャル を表し、 1-3 成分 (= Ai, i = 1, 2, 3 ) は 磁気ポテンシャルを表している。
つまり "光子" は 単なる 数学上の記号にすぎず、物理的実態を意味していないのである。
(Fig.13) もし 電場が "光子" なら・・

もし ある荷電粒子の周りの電場が 光子で形成されているとしたら、これらの光子は 中心の荷電粒子 (= e+ ) から コンスタントに生成放出されていることになる。
これはつまり 荷電粒子内の 光子の ストックが 時間の経過と伴に なくなってしまうということだろうか?
これは 非常に奇妙である。
(Fig.14) 単一光子の大きさは? → 問うこと自体に意味がない?

相対論的な場の量子論は 単一光子が 点状粒子であると主張している。
もしそうだとすると、その点状粒子は どうやって このページに示したように 偏光することができるのだろうか? はっきり言って 不可能である。
X 線と マイクロ波 (= 両方とも単一光子 ) の波長は それぞれ 約 1 pm と 1 m と まったく異なっている。
"熱" 自身も 1種の光子だと 彼らは主張している。
(Fig.15) ビッグバンの赤方偏移で "大きな光子" に引き伸ばされる ? 仮想光子 ?

このページに示したように、彼らは 宇宙が膨張する中、単一光子の波長が 赤方変異によって 引き伸ばされるとしている。
それなら この非常に引き延ばされた 大きな光子は 2つに 切断できるぐらいになったのだろうか?
もし あなたがたが 物理学者の誰かに "単一光子の大きさって どれくらいなの?" と質問しても、おそらく 彼らは "問うこと自体に意味がない。" とか "光子には明確な物理像がない" などと繰り返すだけで はっきりとした回答は得られないだろう。
さらに 電磁場は 相対論に 反する 仮想光子から できているとされている。
実は この "光子" という曖昧で奇妙な概念は その曖昧さゆえに 現在の科学の発展を阻害している 主犯人の1つなのである。
すみやかに この光子の実態を明確にし、さもなければ 単なる電磁波であることを認めるべきである。
(Fig.16) ミュー粒子 → 電子 + ニュートリノ ← 素粒子 ?

ミューオン ( ミュー粒子 ) は 1936 年に 霧箱の中で発見された。
この ミューオンは 瞬く間に ( 寿命 = 2 × 10-6 秒 ) 電子とニュートリノに 崩壊してしまうのに、どうして 私達は このミューオンを素粒子と呼んでいいのか ?
宇宙線内のミューオンは 電子よりも 容易に 物質内を通過できるため、彼らは ミューオンは 電子の 約 200 倍の重さであると結論づけてしまった。
常識的に考えれば、この非常に不安定なミューオンは 高エネルギー状態の 電子 もしくは 陽子の姿と考えるのが自然である。
( 地上に届く宇宙線の ほとんどは ミューオンのため、それは 実は ありふれた粒子であると考えるのは自然である。 )
素粒子は 粒子の根源的な存在のため 基本的に 安定であると考えられるのに、この不安定さは おかしいと言わざるを得ない。
(Fig.17) 粒子の質量と速度を 独立に知ることはできない。

もちろん、1936 年当時 TOF (= 飛行時間測定 ) 装置なんてものは なかったため 粒子の速度を独立に求めたりはしなかった。
要するに 彼らは 霧箱内で ある磁場 (= B ) の状況下での 粒子の軌跡のパターンから ミューオンの質量を推定したのである。
Fig.17 に示したように、 ローレンツ力 (= evB ) が 遠心力に等しいと仮定すると、その動く粒子の 運動量 (= p ) を知ることができる。
重要な点は 霧箱からの情報では 粒子の質量と速度を分けて知ることは 不可能だということである。
なら なぜ 彼らは この新しい粒子ミューオンが 電子の 約 200 倍であると 結論づけることができたのだろうか?
(Fig.18) 動く粒子の エネルギー消失率 ?

彼らは Fig.18 の関係式を用いて 各粒子の質量を推定したにすぎないのである。
Fig.18 は 霧箱内を通過する 動く粒子の エネルギー消失率 を表したものである。
速度 v が 光速度 c より かなり遅いとき、
(Fig.19)

Fig.19 より、粒子の速度 (= v ) が 遅くなるにつれて、それは より多くのエネルギー (= E ) を失いやすくなると 彼らは主張している。
つまり Fig.18 の関係式が正しいとすると、奇跡の長さから 各粒子の速度を知ることができることになる。
しかし もちろんのこと、非常に高速度の粒子まで Fig.18 の関係式が成り立つ保証は まったく
ない。
( 宇宙線内の ミューオンの速度は ほぼ 光速である。)
そのため 当時の物理学者で Fig.18 の関係式は 高エネルギー領域で 破綻する可能があるため、ミューオンは 単に 高エネルギーの 電子もしくは 陽子ではないかと主張した人達も結構いたらしい。
(Fig.20) TOF 法は 必ず正確な測定ができるわけではない。

現在では 飛行時間測定 (= TOF ) 検出器が 主に 反陽子や 陽電子などの 反粒子と 電子、陽子との区別に使用される。
重要な点は、検出シグナルの機器内の伝達速度などのため TOF の検出できる速度には限界があるということである。
当然、宇宙線内、もしくは 加速器内で ほぼ光速度近い粒子の速度を正確に測ることは
不可能である。
低速度の粒子でさえ、TOF は 必ずしも正確な速度をだせるわけではない。
ある粒子の速度を測定するには、異なった時間での その粒子の正確な位置情報を検出する必要がある。
当然、その粒子が各検出器 (= d1 - d4 )にぶつかった影響で、粒子の速度や向きが 変化する可能性は十分にある。
つまり 予期できない散乱効果のために 測定誤差が生じることになる。
さらに、反粒子の数は 基本的に 電子や陽子などに比べて 各段に少ない。
つまり 他のありふれた粒子と ごっちゃになって 誤った認識の原因になる可能性も十分にある。
非常に不安定な反粒子の実在性は 疑わしいと言わざるを得ない。( このページも参照のこと。 )
(Fig.21) π中間子や ミューオンは実在するのか ?

同じことが 非常に不安定な π (パイ) 中間子に関しても言える。
彼らは 霧箱内での 粒子の軌跡の長さなどから その質量を推定したにすぎない。
つまり これらの非常に不安的な粒子は 単に 電子、もしくは 陽子 ( や イオン ) の可能性もあり得るのである。
Fig.21 は 霧箱内での 単純な散乱事象を示しているだけと思われる。
私達は そんなに容易に 新粒子を 増やすべきではない。
本当の統一理論を得るには、多すぎる素粒子の数を 大幅に 減らさなければならない。
(Fig.22) 1/3 クォークは 本当に実在するのか?
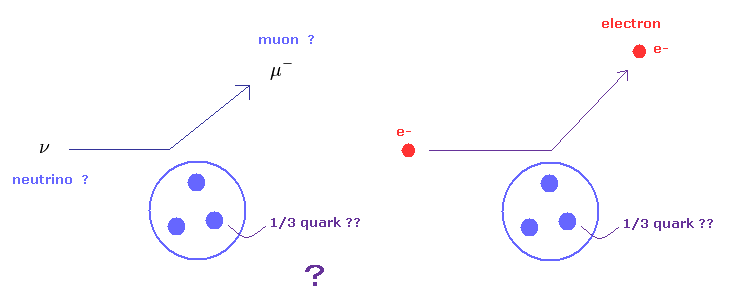
今までに +2/3e や -1/3e などのクォークの分数電荷は 実験で見つかっていない。
現在の標準模型によれば、強い力のために 各クォークは 絶対に 単離することはできないことになっている。
クォークの実在性が 非常に疑わしいのに、どうして 彼らは クォークが リアルだと主張できるのだろうか?
クォークの実在性の証拠で 最も重要なのは 原子核に対するニュートリノの深非弾性散乱である。
しかし実際は、これらの散乱実験は 原子核内部に 想像上の 海クォーク という架空の存在を仮定して 初めて成り立つという おかしなものなのである。
例えば、1つの陽子は 2つの アップクォークと 1つの ダウンクォークを含んでいる。
しかし 標準模型は 陽子には "ストレンジ" クォーク や 反クォーク などの 様々なクォークが詰め込まれていると主張している。
これらの 仮想のクォークを "海クォーク" と言う。
見てのとおり、この理論は 非常に 人為的な仮定のもとに成り立っているのである。
(Fig.23) 各クォークは 陽子の 1/3 ではない?
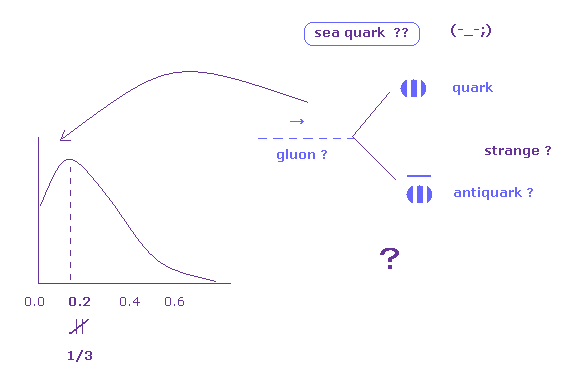
Fig.23 に示したように ( このページも参照のこと )、 電子の散乱実験では 各クォークのエネルギー ( 運動量 ) は 陽子全体の 1/3 未満であることを示している。
つまり これらの散乱実験は -1/3e や 2/3e の分数電荷の確かな証明にはなっていないのである。
この問題を解決するために 非常に人為的な "海クォーク" なるものを導入した。
"海クォーク" とは、陽子内部の クルーオンが クォークと反クォークのペアを次々に生成した結果のものであるらしい。
この 仮想の海クォークのために 各クォークの運動量は 1/3 以下になったと主張している。
もちろん この海クォークなるものは 直接観測することはできず、単なる想像上の産物にすぎない。
(Fig.24) ミューオンの 陽子もしくは 中性子との散乱。
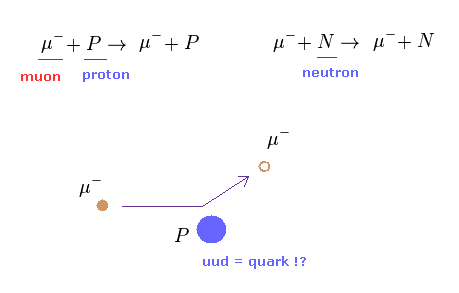
彼らは ミューオン (= μ ) が 陽子もしくは 原子核から どのように散乱されたかを調べた。
これらのミューオンは 原子核内部の クォークの電荷によって散乱されるため、通常の クーロン散乱ということになる。
このページに示したように、古典的なラザフォードの クーロン散乱では、 衝突断面積は 各電荷の二乗の和に 比例することになる。
陽子は 2つの アップクォークと 1つの ダウンクォークを含んでいるはずだが、彼らは Fig.25 に示した 非常に奇妙な 陽子構造を用いている。
(Fig.25) 陽子は これらすべてのクォークを含んでいるの ?? ↓ 海クォーク

Fig.25 は 単一陽子の 構造因子であり、陽子内部の 構造を表している。
驚くべきことに、彼らによれば 単一の陽子内部には アップ、ダウン、ストレンジ クォーク と それらの反粒子の6種類のクォークを含んでいることになっている。
( これらの 仮想粒子を "海" クォーク という。)
つまり これらの散乱実験の仮定は 最初から 間違った定義に基づいているのである。
例えば、アップクォークの電荷は +2/3e であるため、 2/3 の2乗は "4/9" となる。
また ダウンクォークの電荷は -1/3e であるため、その2乗は "1/9" となる。
(Fig.26) 中性子の構造因子 ?? これは奇妙である。

奇妙なことに、彼らは 中性子の構造因子を Fig.26 のように仮定した。
ダウンクォークは -1/3e の電荷を持っているのに、その2乗は 1/9 ではなく4/9 になってしまっている。
これらの仮定は 非現実的な "対称性" に基づいている。
(Fig.27) 原子核の 平均の構造因子。

Eq.25 と Eq.26 から、原子核の平均の構造因子は Fig.27 のようになる。
(Fig.28) ニュートリノ散乱。

最も重要な実験は ニュートリノを用いた 深非弾性散乱である。
もちろん、ほとんどすべてのニュートリノは 検出することができないので、彼らは ミューオンを 弱い相互作用の結果として用いている。
クーロン散乱では 入射した荷電粒子は 何かしらの散乱を必ず受けるが、このニュートリノ散乱は、弱い相互作用が起こらず 素通りする確率がかなり高いため、通常の散乱とは まったく意味あいが異なると言っていい。
しかし 彼らは このニュートリノ散乱の結果を 他のクーロン散乱との比較に用いているのである。奇妙としか言いようがない。
(Fig.29) ニュートリノによる構造因子 ?

仮想の 海クォークを用いて、彼らは 原子核の構造因子を Fig.29 に示すように仮定した。
弱い力では 各電荷に関係ないため、Fig.29 の係数に "4/9" や "1/9" などの数値は含まれていない。
(Fig.30) ニュートリノによる 陽子と中性子の構造因子?

奇妙なことに、 彼らは 陽子と中性子の構造因子を Fig.30 のように仮定した。
もちろん、陽子は 2つの アップクォークと 1つの ダウンクォークを含んでいるはずなので Fig.30 の仮定は 間違いである。
(Fig.31) 原子核の平均の構造因子 ?

Fig.28 と Fig.30 から、平均の構造因子は Fig.31 のようになる。
"ストレンジ" クォーク (= s ) が ほぼゼロと仮定すると、 Fig.27 (= ミューオン散乱 ) と Fig.31 (= ニュートリノ散乱 ) の比は、
(Fig.32) ミューオンとニュートリノ散乱比?

この "5/18" という比は 実験で確認されたと 彼らは主張している。
これが 分数電荷における 最も重要な実験的証拠となっているのである。
このセクションで説明したとおり、これらの仮定は 完全に非現実的な 海クォークに依存している。
陽子が 2つの アップクォークと 1つのダウンクォークで構成されている ( 中性子 = 2 × "ダウン" + 1つの "アップ" クォーク ) ことを考えると 本当の構造因子は次のように ならなければならない。
(Fig.33)
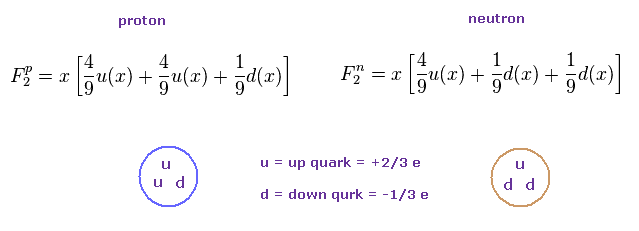
つまり 原子核の平均の構造因子は
(Fig.34)

Fig.34 は Fig.27 と 完全に 異なっている。
よって これらの散乱実験は 誤った仮定に基づいていることが分かる。
さらに 彼らは "見えない" ニュートリノを ミューオンとの比較に用いている
ニュートリノの ほとんどすべてが 弱い相互作用を 起こさず 通りすぎることを考えれば、ニュートリノが 原子核と相互作用する確率は ランダムであり、知ることは不可能である。
つまり ニュートリノに基づいた比というのは 非常に疑わしいと言わざるを得ない。
(Fig.35)

強い力 (= QCD ) の結合定数 αs は 強すぎて 通常の摂動計算が適用できない。
つまり 近似的な数値計算に頼らざるを得ないのである。
要するに QCD は 人為的な 定義や アルゴリズムに頼らなければ 何も予測することができないのである。
(Fig.36) 格子ゲージ理論は ローレンツ対称性を破る。

数値計算をするには、有限の間隔 (= a ) を持つ 格子構造を採用しなければならない。
この格子では、クォークなどのフェルミ粒子は 点、グルーオンは 2つのフェルミ粒子を繋ぐ
"リンク" で表される。
もちろん、この格子ゲージ理論は ローレンツ対称性を 破るため、様々な計算結果から 連続極限 ( a → 0 ) のときの 真の値を 推測 (= 外挿 ) する必要がある。
この不定性が 様々な 誤差を引き起こす。
(Fig.37) クォークの質量は どのように決まったのか ?

実は、アップ、ダウン、ストレンジクォークなどの 軽いクォークの質量は 実験で 測定することは できない。
それなら これらのクォークの質量は どのように決まったのだろうか?
これらの軽いクォークの質量は QCD における フリーのパラメーターで 自由に操作することができる。
これらの質量を決定するには 3つの ハドロン ( 中間子など ) の質量の実験値が必要になる。
しかし Fig.37 に示したように、これらのクォークの質量は 単一の値に決まらない。
( アップクォークの質量の範囲は 1.7 - 3.3 MeV で 2倍ほどの開きがある。 ).
これらの結果は QCD の数値計算が 様々な誤差を引き起こしていることを示している。
(Fig.38)

ご存じの通り、通常の理論では 確率振幅は eiHt のように変化する。
これはつまり 確率は 三角関数のように振動して定まらないことになる。
確率が定まらなければ、数値計算ができず ハドロンなどの質量を数値計算することができない。
Fig.38 では、 Z は 分配関数で、 L が 古典力学におけるラグランジアンである。
(Fig.39) "虚数" 時間は リアルなのか ?

そのため ウィック回転で "実時間" を "虚時間" に変える必要がある。
もちろん、虚時間は 非現実的であるため、QCD による計算結果は 根本的に 非現実的であることに変わりがない。
Fig.39 に示したように、虚時間を使うと、確率振幅が 指数関数のようになり、振動しない。
( = ユークリッド時空間 )
この変換は 計算のためだけにしたもので、リアリティーが消失してしまったと言える。
(Fig.40) 経路積分 = 多世界にリアリティーはあるのか ?

驚くことに、QCD において 彼らは 奇妙な多世界を信じており、ありとあらゆる経路を計算しようとしている。
もちろん、実際に 無限種類の経路をすべて足し合わせることは不可能なため、何らかのアルゴリズムを用いて、有限の経路を選択することになる。
つまり QCD は 第一原理というよりは、意図的な誘導ができる理論なのである。
(Fig.41) QCD の作用。

QCD の分配関数 Z は Fig.41 のように表される。
Fig.41 では、 作用 SG は グルーオンのみで構成されている。
ψDψ 部分は ディラックフェルミ粒子部分である。
後で述べるが これらの 作用 (= ラグランジアン ) は 実験結果に近づけるよう 自由に変更可能なのである。
つまり これらの部分は 所謂 フリーパラメーターと言える。
(Fig.42) 膨大な経路積分

経路積分は すべての経路を考慮することが原則であるため、この計算には 膨大な時間を
浪費してしまうことになる。
多世界自体にリアリティーがないのに 多大な貴重な時間とコンピューター資源を 無駄に使用することは 非常に 非現実的と言える。 こういった非実在的な研究を 彼らは 本当に ずっと継続していくつもりなのだろうか?
(Fig.43) グルーオンの確率?

格子ゲージ理論では 人為的に 有限の経路を選択する。
( "ハイブリッド モンテカルロ法" など 様々な選択方法がある。 )
グルーオンの経路の発生確率は Fig.43 のように与えられる。
( この SG は ある条件さえ満たせば 自由に変更可能である。 )
(Fig.44) ウィルソン・ループ。

格子 QCD は ゲージ対称性に従う必要がある。
そのため グルーオンは Fig.44 のように あるループを形成する必要がある。
このページに示したように ループを形成すると ゲージ変換のもとで 不変になる。
(Fig.45) フェルミ粒子部分。
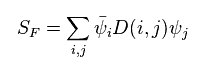
様々なハドロンの質量スペクトラムを得るには、クォークなどの フェルミ粒子が必要である。
フェルミ粒子の作用 S は Fig.45 で与えられる。
この作用は 自由に変更できるため、実際 改良型なども含めて 多くの種類の 作用が存在する。
もちろん、この作用が変化すれば、計算結果も変化してしまう。
つまり 実験値を再現し得る 適切な 作用を 意図的に選択できるのである。
(Fig.46) ウィルソンフェルミオンは カイラル対称性を満たさない。
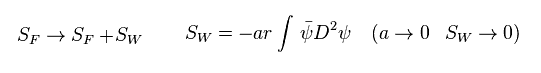
実は、通常の場の量子論と異なり、この格子理論の 作用 S の部分は 自由に変更できる。
Fig.46 に示したように、作用の形が任意でも、それが係数 "a" を持つ限り 連続極限 ( a → 0 ) で この作用はなくなってしまうからである。
フェルミ粒子の作用は "ダブラー" という深刻な問題を引き起こすことが知られている。
この ダブリング問題を解決するために、Fig.46 の項を 人為的に 元のディラックフェルミオンの項に追加した。
これを "ウィルソン・フェルミオン" と言う。
しかし このウィルソンフェルミオンは クォーク質量が ゼロの極限でも カイラル対称性を 満たさないという 別の深刻な問題を 抱えている。
(Fig.47)

これらの作用を用いて、ある ゲージ配位と クォークの伝播関数を得ることができる。
すでに述べたように、格子ゲージ理論は 摂動計算ができず 近似的な数値計算しかできないため、これらのプロパゲーターや グルーオンの配位の仕方には 任意性がある。
当然、これらの配位のパターンによって 計算結果も変わるため、格子ゲージ理論は 第一原理とは呼べない。
問題なのは、これらの計算には 高性能のスーパーコンピューターを何台も同時に使用しても 最低 1年以上の計算期間が 必要になるということである。
( 研究者たちの貴重な人生が 潰れてしまう。)
よって ありとあらゆる配位を調べて 比較するということは 不可能である。
(Fig.47') QCD の数値計算は 恐ろしく時間が かかる ( 1 年以上 ) 。

(Fig.48) π 中間子の伝播関数。
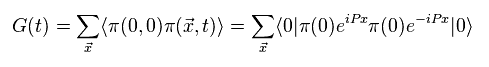
上記の クォークとグルーオンの作用を用いて、 π 中間子の質量を推定することができる。
実は、このハドロンの伝播関数の形においても 様々な異なったパターンを選択できる。
よって 実験値に合う 都合のいい形式を選べばいいことになってしまう。
(Fig.48) 虚時間に基づく π 中間子の質量は リアル なのか?

基底状態のエネルギー (= 質量、 m0 ) は 他の励起状態のものより 小さい。
そのため 虚時間 t が 無限大に近づくにつれ、基底状態の π 中間子の質量 (= 赤線 ) の部分のみが残ると 彼らは主張している。
(Fig.49) π 中間子の有効質量。

時間が十分大きいとき、Fig.48 の最初の項から Fig.49 の関係式を得ることができる。
(Fig.50) π 中間子の有効質量? t = フリーのパラメーター?

π 中間子の安定した値を得るには、 虚数時間 (= t ) を 十分に大きくする必要がある。
しかし Fig.50 に示したように、この時間 t が あまりにも大きくなると、 誤差も大きくなってしまう。
そのため 適当な部分 (= 赤く囲ったところ ) を選んで π 中間子の質量とするしかない。
要するに 時間 t の範囲も 自由なパラメーターと言える。
(Fig.51) フィッティング・パラメーター。

重要な点は QCD を用いて 本当の π 中間子の質量 (= 140 MeV ) を 直接だすことができないということである。
なぜなら 140 GeV の軽い質量をだすのに、非現実的なくらい 膨大な計算時間が かかるからである。
異なった いくつかの質量 (= 200 MeV 以上 ) の値から π 中間子の質量を推定しているにすぎない。
このテクニックを "外挿" という。
もちろん、計算時間の制限があるために すべての地点で計算をすることはできず、2〜3地点のみから、推定するしかない。
QCD の格子ゲージ理論では、軽いクォーク質量のみから すべてのハドロン質量を予想しようとしている。
係数 "A" や "B" .. は フィッティングパラメーター で 自由に調節できる。
(Fig.52)
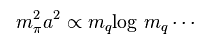
重要な点は これらのフィッティング関数 (= クォークとハドロン質量の関係式 ) は 何でもありだということである。
つまり この関数を 自由に選択できる。
( Fig.51 では 多項式で、Fig.52 では 対数関数である。 )
(Fig.53)

同じように、原子核と クォーク質量の関係式も 任意に選択することができる。
係数 "A", "B", "C" .. などは フリーのパラメーターである。
(Fig.54)

QCD では 本当の軽いクォーク質量を用いて 本当の中間子質量を得ることは不可能である。
Fig.54 に示したように、 実際の値よりも はるかに重い "アップ" もしくは "ダウン" のクォーク質量を用いて、 本当の π 中間子の質量を推定しているにすぎない。
例えば、 50, 150, 200 MeV の "アップ" クォーク質量から 様々な物理量を推定する。
( 本当の "アップ" クォークの質量は たったの 1.7 - 3.3 MeV ではあるが・・ )
もちろん、選択した格子のサイズ (= volume )も 計算結果に影響を与えることは言うまでもない。
よって、実験値を再現し得る サイズを選択できることになる。
( つまり QCD は 第一原理とは とてもじゃないが 呼べない。 )
(Fig.55)

格子間隔ゼロ ( a = 0 ) の値を 直接だすことは不可能である。
そのため、他の いくつかの地点 ( a = 0.2, 0.4 .. ) の計算値から 推定するしかない。
これを "連続極限への外挿" と呼び、様々な 誤差の原因となる。
フィッティングパラメーターを調節することによって、都合のいい計算結果を 選択することが可能となる。
この誤差を減らすために 作用 (= S ) や 計算アルゴリズムを 人為的に変更したりする。
つまり これら 作用や アルゴリズム ( 経路を決める ) も 立派な フリーパラメーターなのである。
(Fig.56)

Fig.55 では、異なったフィッテイング関数を選択すると Fig.56 のように 原子核の質量の 連続極限 ( a = 0 ) での 推定値が 変わる。
結果的に 格子 QCD は 正確な値を予測することができないのである。
単に調節しているにすぎない。
第一に "虚時間" に基づく 計算結果自体に リアリティーが ない と言っていい。
(Fig. 57) カイラル対称性の破れは 原子核質量の 98 % の起源である。

このセクションでは、カイラル対称性の破れの概念が ヒッグス機構に 非常に似ており、それらが 何の具体的な物理的イメージを 持っていないことを説明する。
原子核質量の 98 % は カイラル対称性の破れに基づくもので たった 2 % が ヒッグス機構に由来するとされている。
(Eq.1) 右巻き、左巻きの波動関数。

ディラックのフェルミ粒子の波動関数 (= ψ ) は 右巻きと左巻きの波動関数に分離できる。
"右巻き" とは、スピンと運動量の向きが 同じという意味である。
"左巻き" とは、これらの向きが 互いに逆方向だという意味である。
このページに示したように、これらの波動関数は 次を満たす。
(Eq.2)
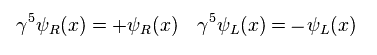
ここで γ5 行列は 次を満たす。
(Eq.3)
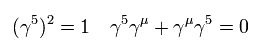
Eq.2 を用いて、 右巻き ( もしくは 左巻き ) の波動関数のみを ピックアップできる。
(Eq.4)
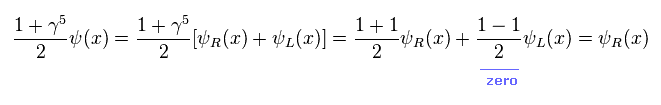
結果的に
(Eq.5)

このページに示したように、ディラック場 (= 電子やクォークなどのフェルミ粒子 ) のラグランジアンは
(Eq.6)
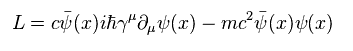
ここでは Eq.6 の質量項 (= 2項目 ) は、
(Eq.7)
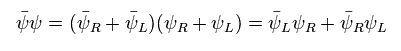
ここで Eq.7 が でた理由を説明する。
Eq.7 では 次の関数は
(Eq.8)
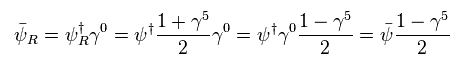
と
(Eq.9)

Eq.8 と Eq.9 から、 "RR" と "LL" の波動関数の組み合わせは ゼロになる。
(Eq.10)

一方で、Eq.6 の運動量項 (= 1項目 ) は、
(Eq.11)

ここで 次の関係式を使う。
(Eq.12)

Eq.8、 Eq.9、Eq.12 を用いて、次を得る。
(Eq.13)

すると Eq.11 を得る。
ここで 次の 位相 ( カイラル ) 変換を考える。
(Eq.14)

Eq.2、 Eq.3、 Eq.14、を用いて、 右 ( もしくは 左 ) 巻きの波動関数は 次のように変換する。
(Eq.15)
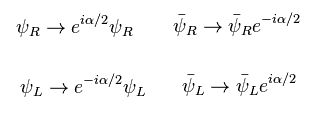
Eq.7 に示したように、質量項は 右巻き、左巻きのペアの項から成る。
つまり この質量項は Eq.15 の位相変換のもとで 変わってしまう。
(Eq.16)

つまり クォークのラグランジアンが 質量項を含んでいると、Eq.15 の変換のもとで 不変では なくなる。
これを "カイラル対称性の破れ" と呼び、原子核質量の起源だと 彼らは主張している。
(Eq.17)

一方で、ラグランジアンの運動エネルギー項は この変換のもとで 不変である。
このセクションで 示したように、このカイラル対称性の破れという概念は 非常に抽象的な 数学的記号にすぎず、何の物理的実態が ない に等しい。
(Eq.18)

このページに示したように、彼らは 左巻きのフェルミ粒子を "行列"、右巻きのフェルミ粒子を "数" と 人為的に 定義した。
質量項が 左巻きと右巻きの関数をミックスしているため、 共通の位相変換を見つけることができない。
(Eq.19)

なぜなら、1つが "行列" で、もう1つが "数" だからである。
つまり ゲージ対称性 (= 位相変換のもとでの不変性 ) を満足するには、この質量項を除去する必要があると 彼らは主張している。
これが ヒッグスボソンを必要とする理由である。
あなたがたは この非常に 抽象的な理由を 理解されただろうか ?

2013/12/5 updated This site is link free.