(Eq.1)
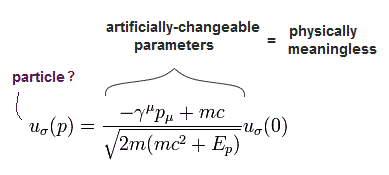
と
(Eq.2)
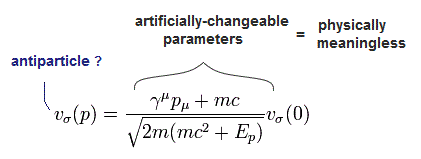
ここで
(Eq.3)
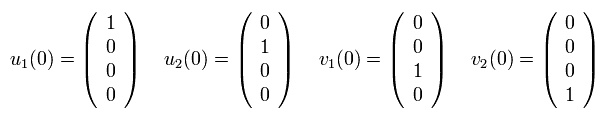
トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは実在しない。
何が実在の素粒子か?
最初に ”左巻き”と ”右巻き”のスピノルについて説明することにする。
はたしてこれらの状態を視覚化することは可能だろうか ??
このページに示したように、 ディラックスピノル u(p) と v(p ) は、
(Eq.1)
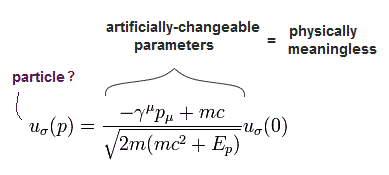
と
(Eq.2)
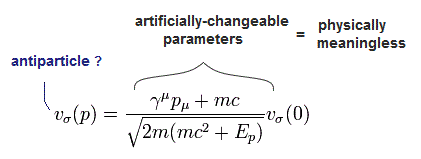
ここで
(Eq.3)
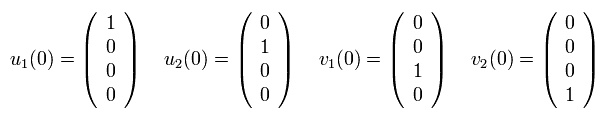
ここで パウリ行列は、
(Eq.4)

また γ 行列は、
(Eq.5)
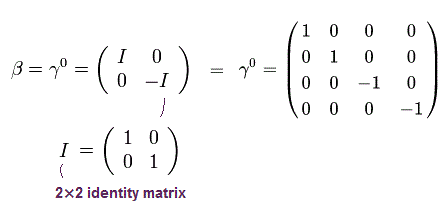
(Eq.6)
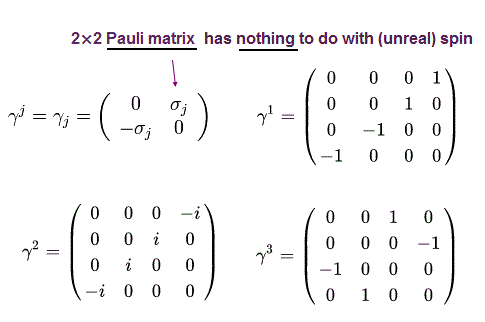
Eq.3、Eq,4、Eq.5、Eq.6 より、 Eq.1 (of u1(p) ) の分子は、
(Eq.7)
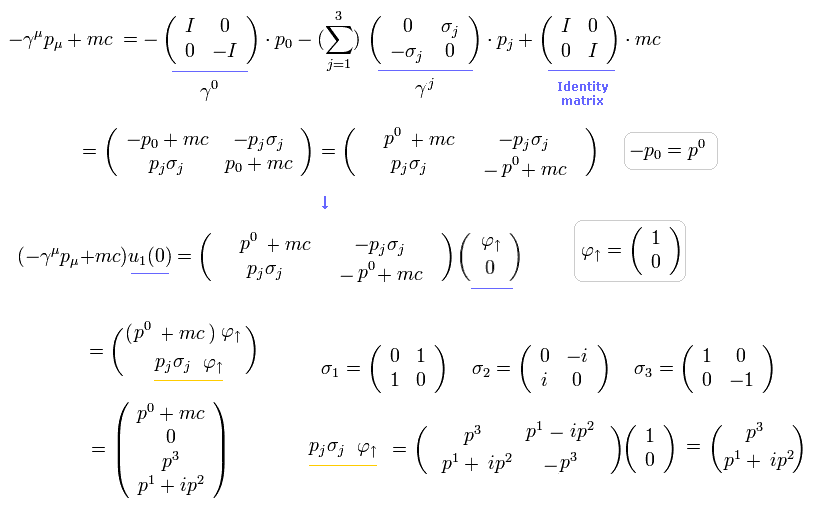
ここでは (-1, +1, +1, +1) バージョンを使用している。
つまり Eq.1 の u1(p) は、
(Eq.8)

同じように、Eq.1 の u2(p) は、
(Eq.9)
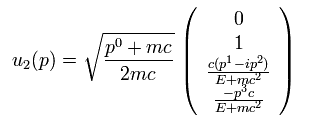
Eq.1 の v1(p) は、
(Eq.10)
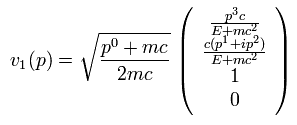
Eq.1 の v2(p) は、
(Eq.11)

ここで 次の γ 行列を使う。
(Eq.12)

この γ5 が u1(p) に作用すると、
(Eq.13)
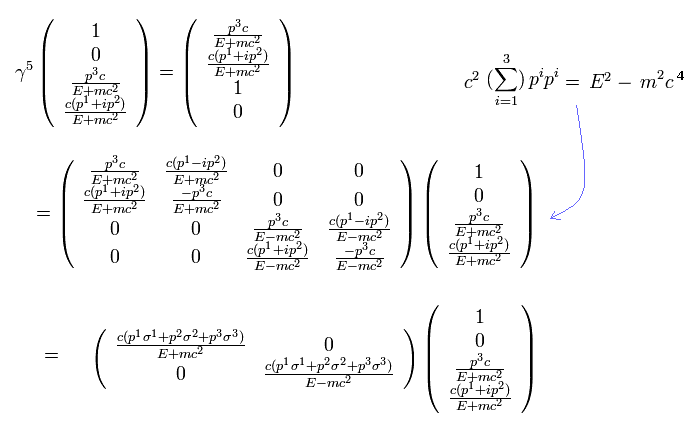
質量 m がゼロで かつ 粒子が z方向へ動いているとき、
(Eq.14)

Eq.14 を Eq.13 の最後の行に代入して、 σ3 に注意すると、
(Eq.15)
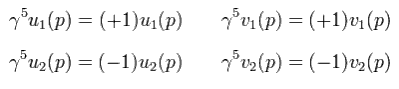
Eq.15 から、
(Eq.16)

もし次のように定義すると、
(Eq.17)

波動関数は次のように分離できる。
(Eq.18)

次の関係式を使う。
(Eq.19)
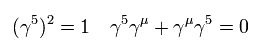
と
(Eq.20)

ディラック方程式は、
(Eq.21)

Eq.21 は、フェルミ粒子の質量がゼロのとき、左巻き (もしくは 右巻き) の粒子のみが残ることを意味している。
( フェルミ粒子が質量を持つと、左巻きと右巻きの粒子が混在した状態になるというわけである。)
しかし、残念ながら 我々は これらの 巻き状態を 具体的に描くことができない。
QED において、断面積を得るには ファインマンダイアグラムにおける確率振幅を計算する必要がある。
まず最初に これらのことは 物理的というより、非常に”数学的”な性質が強いということを言っておく。
このホームページでは、 このページ や このページ の表記を使用する。
(Ap.1)

ある状態をあらわす波束は次のように書ける。
(Eq.22)

ここで 確率すべての合計は 1 になる。
(Eq.23)

またここでは Ap.1 の | k > や 関係式を使っている。
A+B → 1+2 の遷移の確率 (= 確率振幅の2乗) は、
(Eq.24)

ここで iT は S行列の 相互作用項 を含んでいる。
S行列は ある時間の間に 遷移を生じさせる ユニタリ行列を意味している。
そのため、次のように定義することができる。
(Eq.25)

エネルギーと運動量の保存 を意味するデルタ関数は Eq.25 に含まれている。
(これは後で計算する。)
(Fig.1)
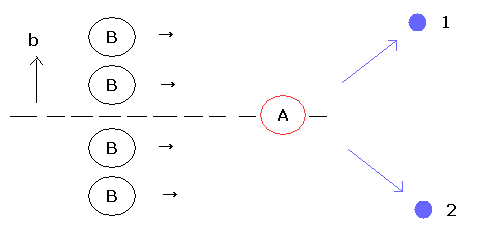
Fig.1 に示すように、B の波束は impact parameter b (=二次元平面) に応じて 均一に分布している。
そのため散乱イベントの回数 (N) と 散乱断面積 (σ) は、
(Eq.26)
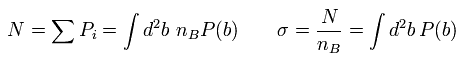
ここでは ある平面上で b によって積分している。
nB は B の数密度を意味している。
Eq.22, Eq.24, Eq.25, Eq.26 を使うと、 (微分) 断面積は、
(Eq.27)

ここで b の指数関数は b のド・ブロイ波 (= 確率振幅 ) を意味している。
Eq.27 は A と B それぞれに 6つの運動量 ( 3 × dkA, and 3 × dkA* ) を含んでいる。
最初に 次のように積分する。
(Eq.28)
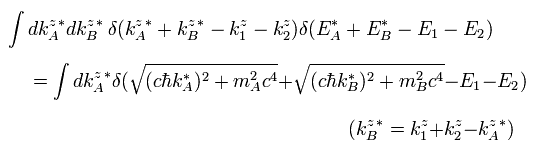
ここで 次のデルタ関数の公式を使う。
(Eq.29)

f(k) が次のとき、
(Eq.30)
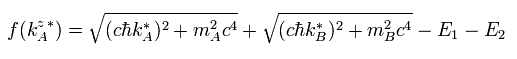
f '(k) は、
(Eq.31)

結果、近似的に E = mc2 とおいて、 Eq.29、 Eq.31 を使うと、 Eq.28 は、
(Eq.32)

ここで 速度 v = p/m、 運動量 p = ħ k である。
次に Eq.27 において、 次の積分をする。
(Eq.33)

また Eq.33 の結果を使って 次の積分をする。
(Eq.34)
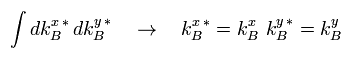
また、Eq.27 で、 次の積分をする。
(Eq.35)

Eq.32、 Eq.33、 Eq.34、Eq.35 から、 Eq.27 は、
(Eq.36)

Eq.23 を考慮すると、 Eq.36 は、
(Eq.37)
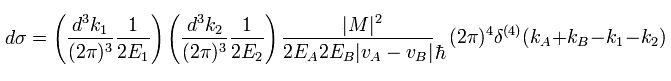
次に 最終状態 2 の運動量 (波束 k) で 次のように積分する。
(Eq.38)

最終状態 1 の dk3 の積分は 立体角を使って 次のように表せる。
(Eq.39)
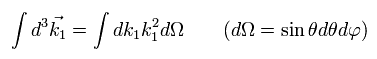
Eq.29 の公式を使って、
(Eq.40)
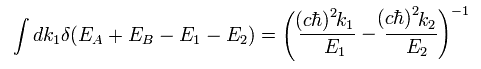
ここで 重心系を仮定する。
(Eq.41)
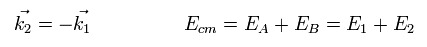
ここで Ecm は全エネルギーである。
Eq.41 から、 Eq.40 は、
(Eq.42)

Eq,38, Eq.39, Eq.40, Eq.42 から、 Eq.37 は、
(Eq.43)
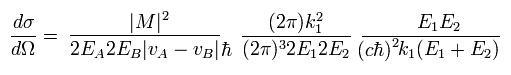
Eq.41 を使って、
(Eq.44)
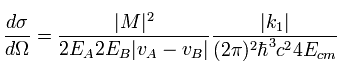
次の近似を使う。
(Eq.45)

ここで | vA - vB | は 近似的に 2c である。
Eq.45, Eq.44 を使うと、
(Eq.46)

これは 立体角に対する微分断面積である。
ここで Eq.46 の次元が メートルの二乗になっていることを確かめる。
基本的に ディラックのデルタ関数の次元は その中に含まれる数の 逆数 になる。
(Eq.47)

波数 (k), エネルギー (E), 光速 (c), プランク定数 (h) の次元は、
(Eq.48)

つまり Eq.25 の M の次元は、
(Eq.49)

ここでは S 行列は 次元なしである。
Ap.1 から、 |k> の 1ペアの次元は E/k3 である。
つまり Eq.46 の次元は、
(Eq.50)

結果的に 微分断面積の次元は メートルの二乗である。
次に QED で最も重要な反応の確率振幅を求める
(Fig.2)
Fig.2 では、高エネルギーの 電子 (e-) と 陽電子 (e+) が 互いに衝突して 仮想光子に変化する。
そして、仮想光子 (光子の伝播関数) が ミューオン (μ-) と 反ミューオン (μ+) に変化する。
この計算過程は クォークと反クォークの生成にもあてはめることができる。
もちろん、これらの最終生成物は 不安定なため、安定な 電子、γ 線、ニュートリノなどにすぐに変化する。
ファインマンダイアグラムや 具体的な計算過程については、 このページも参照のこと。
ここで 最初の状態の電子と陽電子の運動量を PA、PB とする。
(つまり それらの波数は kA と kB である。)
そして、最終産物の ミューオンと反ミューオンの運動量を P1、P2 とする。
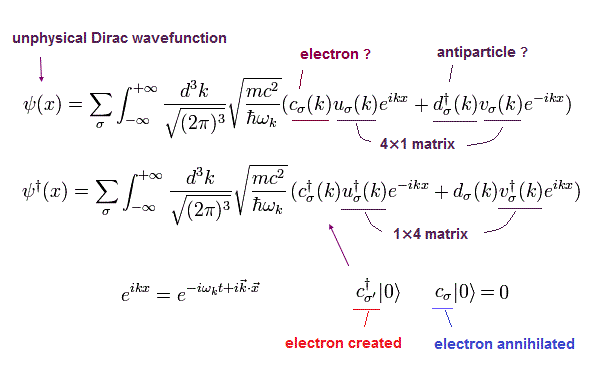
次のディラックの波動関数を使う。
(Eq.51)
これの共役な転置行列 (× γ0) は、
(Eq.52)
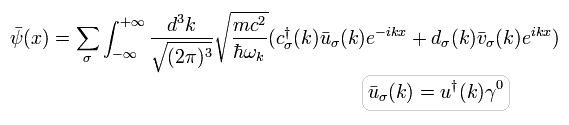
また 光子の伝播関数は、
(Eq.53)
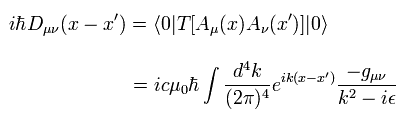
Fig.2 の 確率振幅は、
(Eq.54)

ここで Ap.1 の < k | と | k > を使用した。
Eq.25 から、 M は、
(Eq.55)
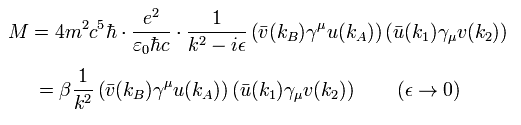
よって M の二乗 ( squared matrix element ) は、
(Eq.56)

このページの Eq.49-Eq.51 のトレーステクニックを使って、 Eq.56 は、
(Eq.57)

ここで Ap.1 の u と v の関係式を使った。
最終状態はすべてのスピン状態をとれて、最初の状態は スピンアップかダウンのどちらか一方の状態である。
よって 1/2 × 1/2 = 1/4 が付加されている。 (ここはちょっと想像するのが難しいが・・。)
Eq.55, Eq.57 から、
(Eq.58)

ここで 次の ガンマ行列のトーレス公式を使う。
(Eq.59)
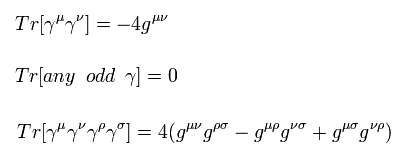
このホームページは (-1, 1, 1, 1) バージョンの軽量テンソルを使用している。
奇数個の γ 行列のトレースはゼロになるため、
(Eq.60)
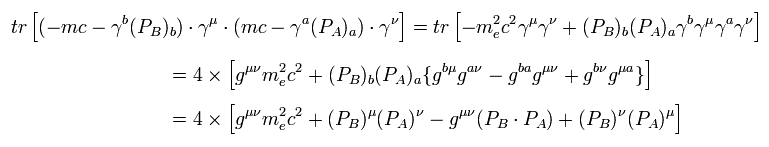
同様に、
(Eq.61)
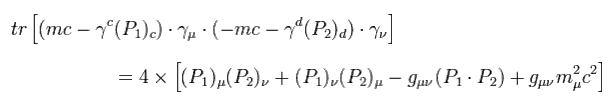
ここで 電子の質量をゼロと仮定して ( me = 0 )、次のような計算をしていく。
(Eq.62)

や

や

すると 次の結果を得る。
(Eq.63)

ここで 電子 (A) と 陽電子 (B) の運動量とエネルギーを次のように仮定する。
(Eq.64)

また ミューオン (1) と 反ミューオン (2) のものは
(Eq.65)

ここで ミューオンの運動方向とz 軸 の間の角度を θ, とする。
(Eq.66)

仮想光子の 運動量とエネルギーは 電子と陽電子のものの合計なので、Eq.64 より、
(Eq.67)

ここで k は 光子の波数である。
Eq.64 から Eq.66 までより、
(Eq.68)
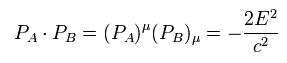

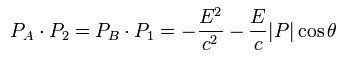
Eq.67 と Eq.68 を使って、 Eq.63 は、
(Eq.69)
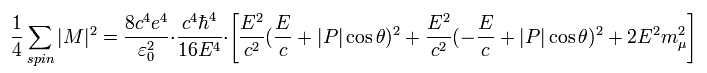
ここで 次のように定義する。
(Eq.70)

Eq.70 を使って、 Eq.44 は
(Eq.71)
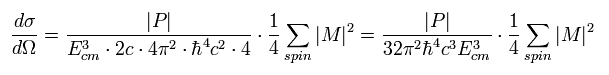
Eq.69 を Eq.71 に代入して、
(Eq.72)

ここで 微細構造定数 α を使った。
この結果は少し複雑だが、重要な点は 散乱断面積は 各電荷に比例するということで、このことは ラザフォード散乱に関しても言える。
しかし γ 行列のトレースなどからして、はっきりいって これらは 物理的性質のものというよりは ”数学上”のものと言える。

2011/12/29 updated This site is link free.