閉曲面の裏返し と ３次元球面 , レンズ空間
球面やトーラスなどの閉曲面（２次元閉多様体）は、ご存知の通り、３次元空間の中では、
裏返すことが出来ません。しかし、４次元空間の中では、簡単に裏返すことが出来ます。
では、球面の裏返しが４次元空間の中で行えることを、右の図で説明します。
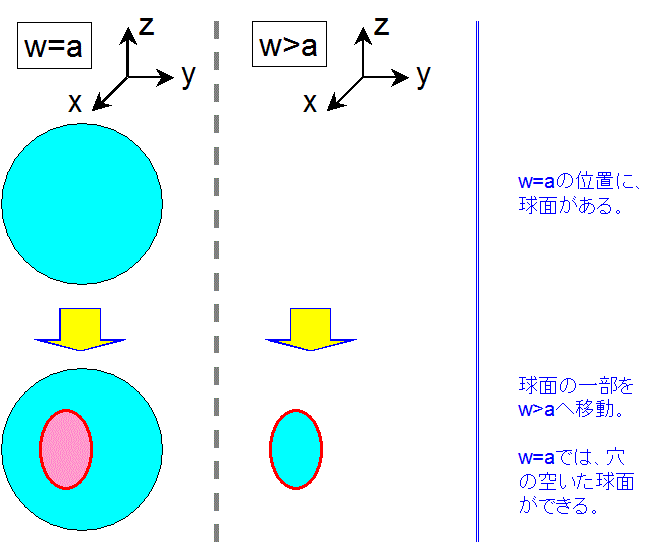
４次元空間の座標軸を、x軸、y軸、z軸、w軸とします。
そして、最初、球面は、w座標が a（w＝a）に固定された３次元空間の中にある、とします。
ここで、球面の表側は、水色で表しておきます。
次に、球面の一部だけを、w座標が aより少し大きい位置（w＞a）へ移動します。そうすると、w＝a での３次元
空間では、球面から、穴の空いた球面へ変わります。その結果、穴の向こうに、球面の裏側が見えて来ます。なお、
球面の裏側は、ピンク色で表しています。
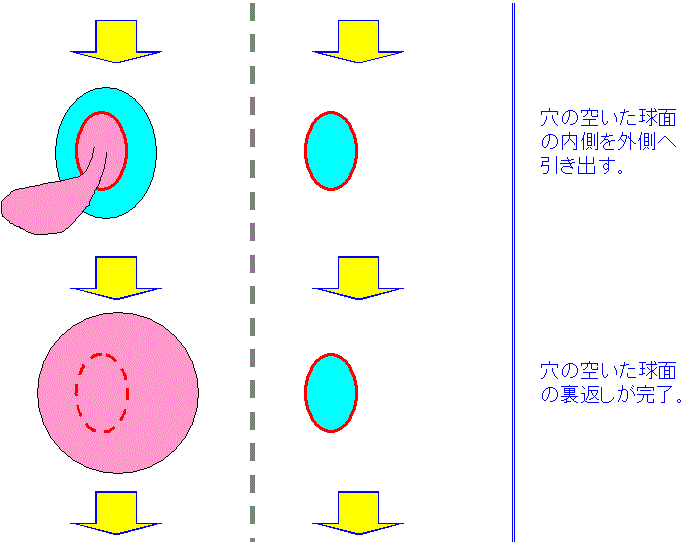
そして、穴の向こうの裏側の面をつまんで、穴の手前へ引っ張り出します。
この引っ張り出しが全て終わると、裏側（ピンク色）が表になります。すなわち、裏返しが完了します。
最後に、w＞a に移動していた球面の一部を、w＝a の位置に戻します。その結果、w＝a での３次元空間の中の
球面に戻ります。ただし、最初の球面の裏側と表側が、すっかり入れ替わっているのです。すなわち、球面の裏返し
が出来たことになります。
上述の球面の裏返しと同様に、４次元空間の中では、トーラスの裏返しやｎ重トーラス（ｎ≧２）の裏返しも、
簡単にできます。ここで、ｎ重トーラスとは、ｎ個の穴のあるトーラスのことです。
ところで、３次元球面から球体を取り除いた残りの部分は、球体に変形することが出来ます。なぜなら、上述の
ように、球面の裏返しが出来るからです。このことは、３次元球面が２つの球体に分解できることを意味します。
逆に言うと、２つの球体を貼り合わせると、３次元球面が出来ることになります。
この辺りのことを、右の図を用いて、詳しく説明します。
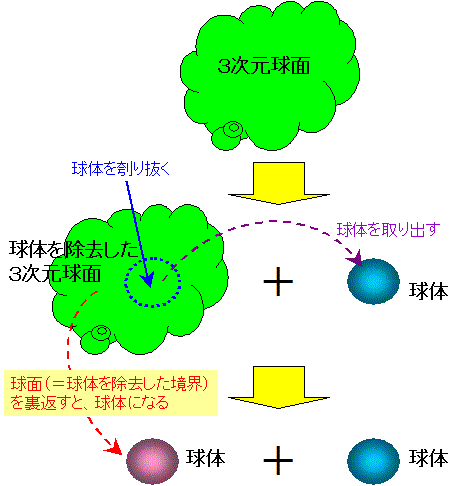
まず、１つの３次元球面があるとします。右の図では、３次元球面を、便宜的に、雲のような形に表しました。
（３次元球面の実際の形のイメージは、『
３次元球面 と Ｓ2ＸＳ1 多様体 』 を、ご参照ください。）
次に、３次元球面から、球体を刳り抜き、取り出します。すなわち、３次元球面を、球体を除去した３次元球面と、
球体に分離します。
球体を除去した３次元球面では、球体を除去した境界が球面になっています。この球面を裏返します。すると、
球面の外側の３次元領域が、球面の内側の３次元領域に変わります。すなわち、球体を除去した３次元球面は、
境界である球面の裏返しを行うことで、球体に変わります。
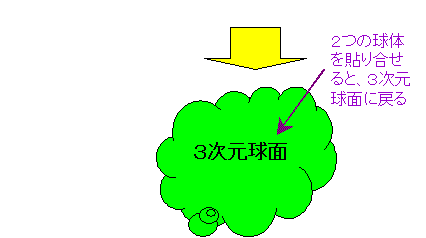
２つの球体を貼り合せることで、元の３次元球面に戻ります。（２つの球体を貼り合わせると、３次元球面になる
ことについては、『 ３次元球面 と Ｓ2ＸＳ1 多様体 』 を、
ご参照ください。）
同様にして、トーラス体を除去した３次元球面は、トーラス体に変形できることがわかります。なぜなら、トーラス
の裏返しが出来るからです。すなわち、３次元球面は、２つのトーラス体に分解できることがわかります。
さらに、ｎ重トーラス（ｎ≧２）の裏返しが出来ることから、ｎ重トーラス体を除去した３次元球面は、ｎ重トーラス体に
変形できます。そして、３次元球面は、２つのｎ重トーラス体に分解できることがわかります。
ところで、３次元多様体Ｍが２つの種数ｎのハンドル体（注）に分解できるとき、
『Ｍは種数ｎのヒーガード分解を持っている』、と言います。そして、種数ｎのヒーガード分解を持つ時、ｎ以上の任意の種数
でもヒーガード分解を持ちます。なお、ヒーガード分解の出来る最小の種数を、ヒーガード種数と呼んでいます。また、
一般に、任意の向き付け可能な閉３次元多様体は、ヒーガード分解を持っています。
（注） 球体は種数０のハンドル体、トーラス体は種数１のハンドル体、
ｎ重トーラス体（ｎ≧２）は種数ｎのハンドル体です。
では、いくつかの３次元多様体について、ヒーガード分解やヒーガード種数を紹介しておきます。
まず、３次元球面は、任意のｎ（ｎ≧０）に対して種数ｎのヒーガード分解を持っており、ヒーガード種数は０です。
次に、Ｓ2ＸＳ1 多様体や３次元実射影空間などは、
種数１のヒーガード分解を持っており、ヒーガード種数は１です。また、ポアンカレ球面は、種数２ののヒーガード
分解を持っており、ヒーガード種数は２です。そして、３次元トーラスは、種数３のヒーガード分解を持っており、
ヒーガード種数は３です。
ところで、種数１のヒーガード分解が出来る３次元多様体のことを、レンズ空間と呼んでいます。
そして、レンズ空間は、L(p,q) と言う記号で表されます。なお、この p や q は整数で、２つのハンドル体の貼り合わせ方を表すものです。例えば、
３次元球面は L(1,q)、Ｓ2ＸＳ1 多様体は L(0,1)、３次元実射影空間は L(2,1) と表すことが出来ます。なお、レンズ空間 L(p,q) の
基本群は、p≠0 の場合は位数 p の巡回群となり、p＝0 の場合は Ｚ＝｛ 0, ±1, ±2, ±3, ・・・ ｝ ： 整数全体の加法群 となります。
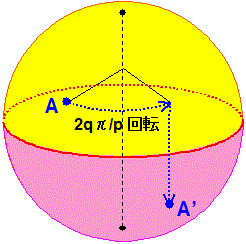
なお、レンズ空間 L(p,q) は、右図のように、球の赤道（球の中心を通る平面と球面の交線。右図の赤線）より上の半球面（右図の黄色の部分）
を 2qπ/p 回転したものを、赤道より下の半球面（右図のピンク色の部分）と貼り合わせることでも得られます。すなわち、右図において、
上半球面上の点 A は、下半球面上の点 A' と重なることになります。
また、一般に、ある整数 k について qq'＝kp±1 が成り立つとき、レンズ空間 L(p,q) とレンズ空間 L(p,q') は位相同形となります。例えば、
L(4,1) と L(4,3) は、p＝4 、q＝1 、q'＝3 、k＝1 → qq'＝3＝4−1＝kp−1 であるから、位相同形となります。このように位相同形となることは、
右図を用いることでも理解できます。まず、L(4,1) は、上側半球面を π/2 回転して下側半球面と貼り合わせた多様体です。また、L(4,3) は、
上側半球面を 3π/2 回転して下側半球面と貼り合わせた多様体ですが、上側半球面を右図とは逆方向に π/2 回転して下側半球面と貼り合わせた
多様体と考えることもできます。すなわち、4次元ユークリッド空間内で考えると、L(4,3) は L(4,1) の鏡像対称体となっています。また、4次元
ユークリッド空間内において 3次元多様体を適宜に移動すると、元の多様体とその鏡像対称体の区別は付かなくなります。すなわち、4次元ユークリッド
空間内で考えると、L(4,1) と L(4,3) は位相同形となります。
参考資料： ・下記URLに掲載のPDFファイル
http://www.komazawa-u.ac.jp/~w3c/lecture/pdf/waseda.pdf#search='%E3%83%AC%E3%83%B3%E3%82%BA%E7%A9%BA%E9%96%93'
・下記URLに掲載のPDFファイル
http://tunnel-knot.sakura.ne.jp/3-manifolds.pdf
