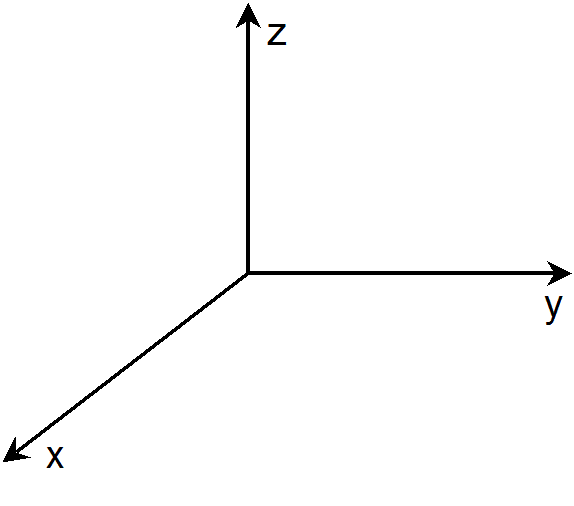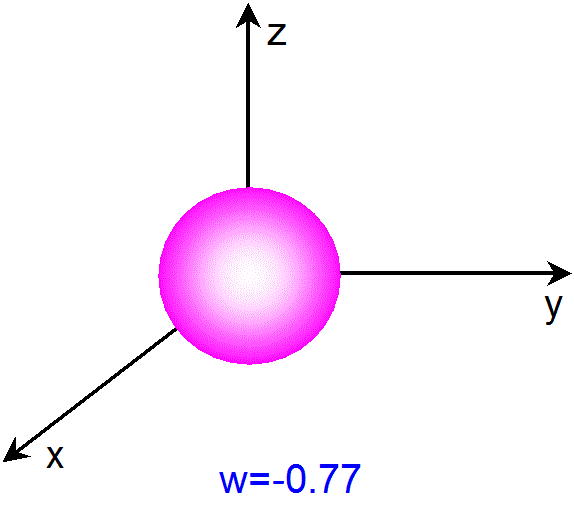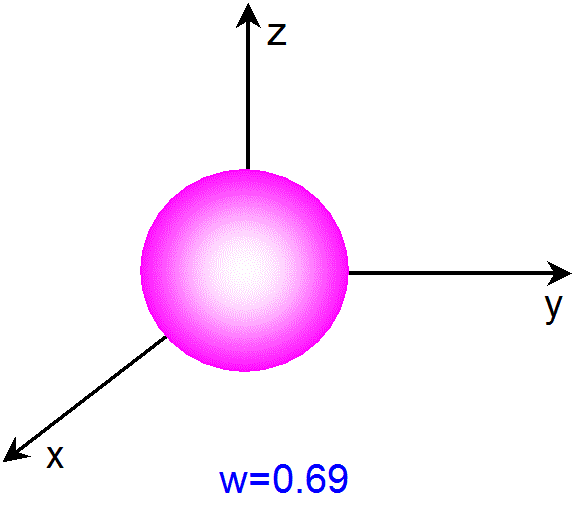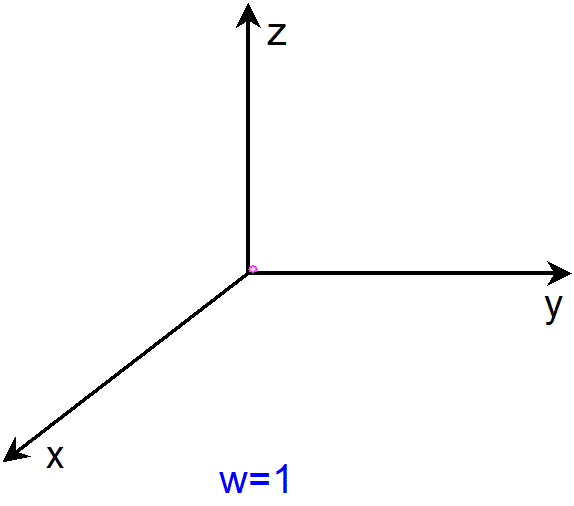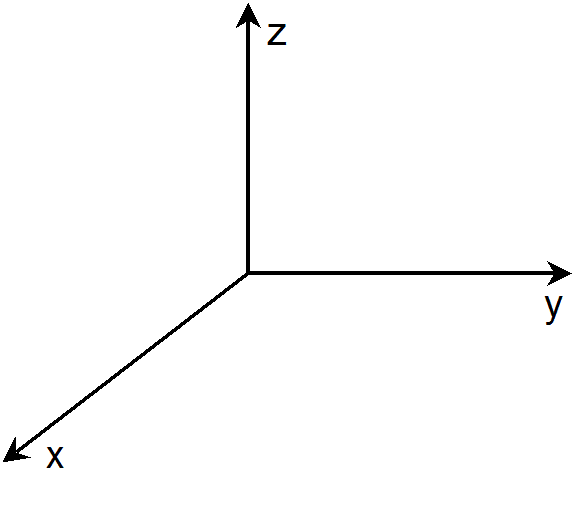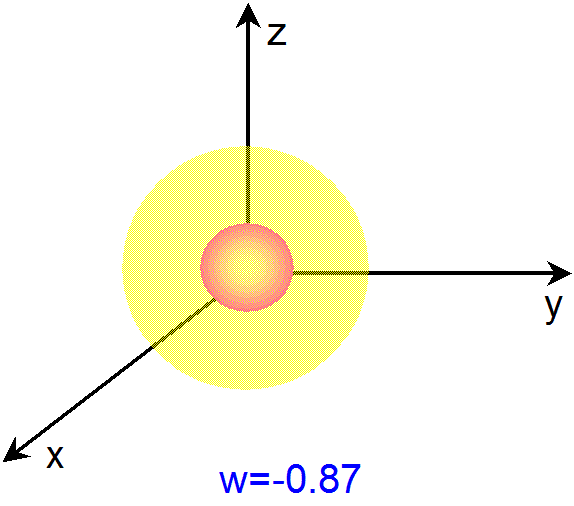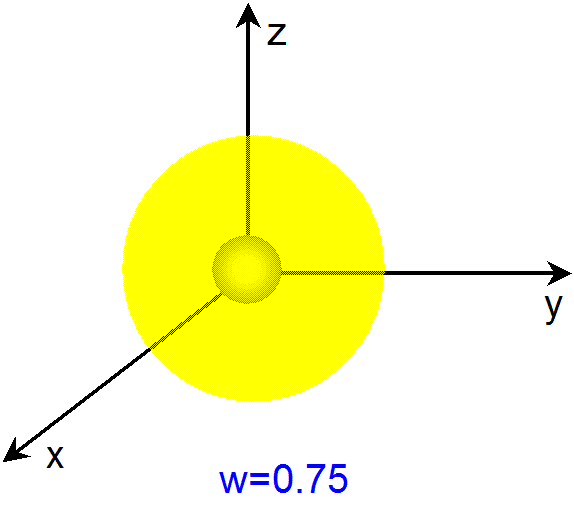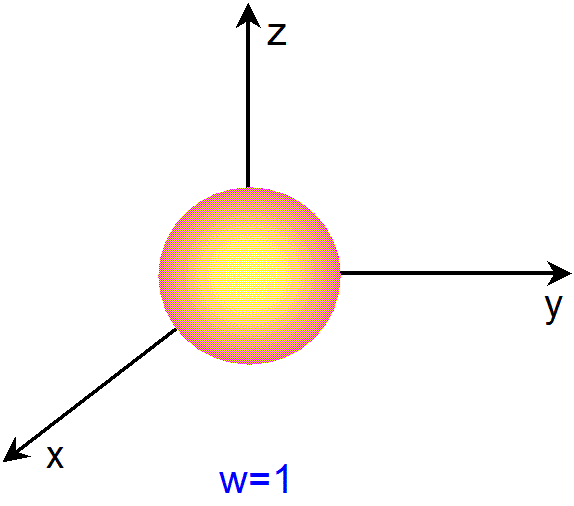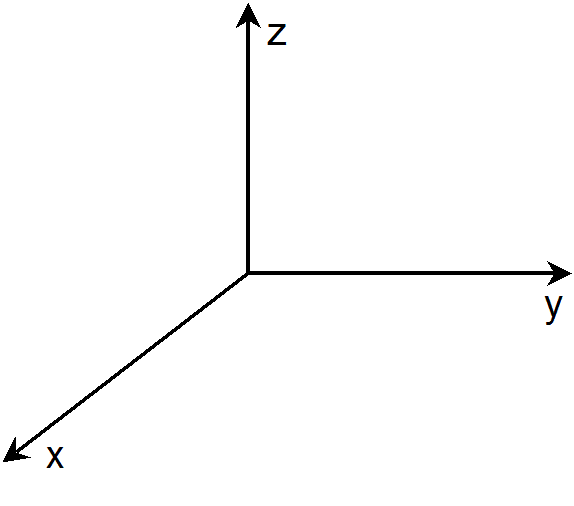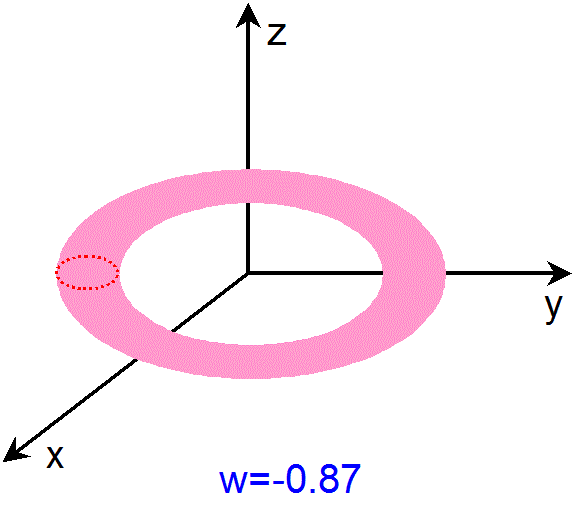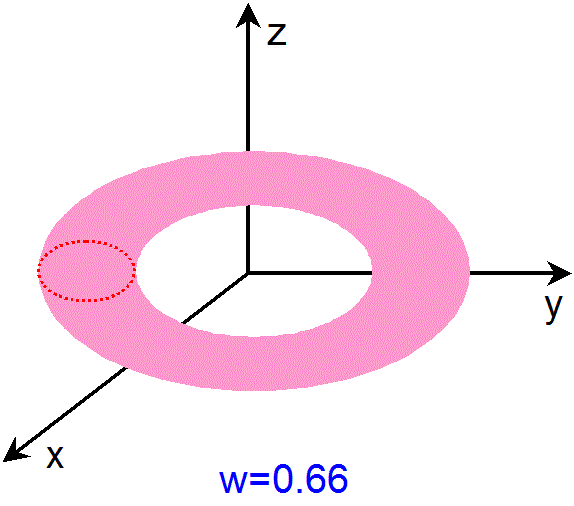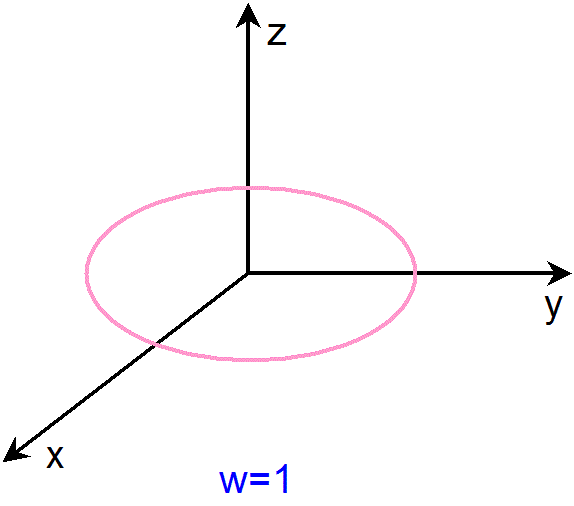3次元球面 と S2XS1 多様体
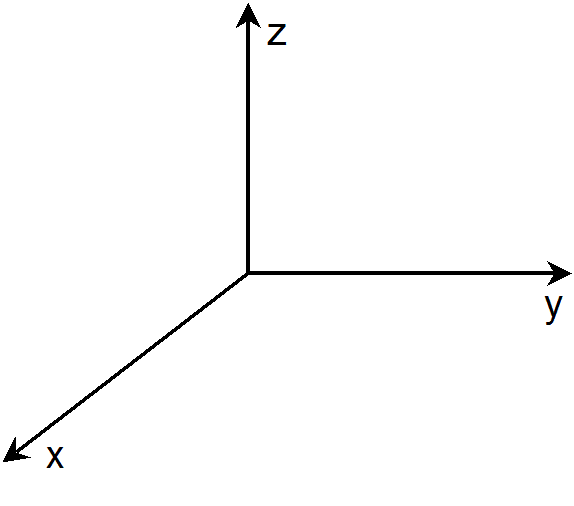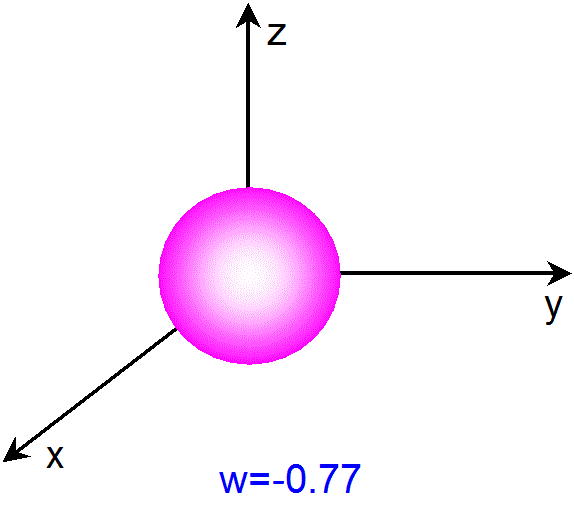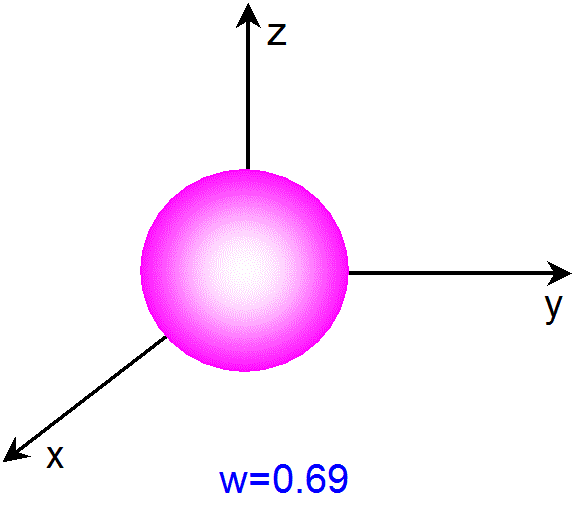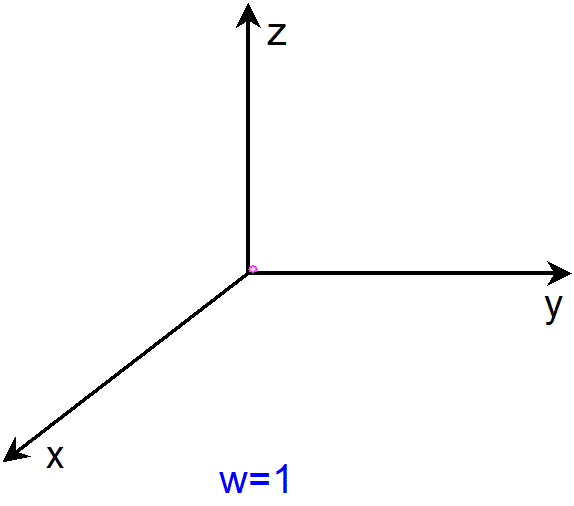
3次元球面のGIFアニメーション(GIF animation)を作ってみました。右のアニメーションです。
w軸を時間軸に置き換えて、アニメーションにしてみました。3次元球面の形をイメージするのに、少しは役に立つかもしれません。
では、このアニメーションについて、説明します。なお、以下の説明中で、単に『球面』と言った場合は、2次元球面(普通の球面)を
指しているものとします。
まず、アニメーションを構成している各々の図は、4次元空間内にある3次元球面を、wをある値に固定した3次元空間で切った断面です。
普通、『断面』と言うと、面(2次元空間)を連想しますが、ここでの断面は、3次元空間です。このアニメーションは、w を -1 から
1 まで変化させながら、各 w での断面(=3次元空間)を次々に示しています。すなわち、右のアニメーションの中で、次々に現れて来る
ピンク色の球面は、3次元球面の各 w での断面(=3次元空間)を示しています。
アニメーションをご覧になるとわかる様に、まず、w=-1 や w=1 での3次元球面の断面は、半径ゼロの球面、すなわち、1点(x=y=z=0)
です。また、w=0 での3次元球面の断面は、半径1の球面です。そして、w=a(-1<a<1)での3次元球面の断面は、半径が
(1-a2)1/2 の球面です。すなわち、全ての断面において、球面上の点は、
x2+y2+z2+w2=1 の関係を満足していることがわかります。一目瞭然ですが、この式は、
x、y、z、w の対称式になっています。すなわち、x、y、z、w の任意の入れ換えが可能です。例えば、x軸の代りに y軸、y軸の代りに z軸、
z軸の代りに w軸に、それぞれ置き換え、w軸ではなく x軸を時間軸とするアニメーションを作った場合でも、右のアニメーションと全く同じ様に、
ピンク色の球面が動きます。
なお、このアニメーションでは、説明を簡単化するため、半径を1としましたが、半径をRとしても、全く同様であることは言うまでもありません。
ところで、球面は、2次元閉多様体の一種です。すなわち、球面の上のどの点においても、その周囲の2次元方向に広がりを持っています。
言い換えると、球面は、2次元の閉じた空間になっており、2次元的な境界は存在しません。
3次元球面も、球面と同様に、説明することができます。3次元球面は、3次元閉多様体の一種です。すなわち、3次元球面の中のどの点に
おいても、その周囲の3次元方向に広がりを持っています。言い換えると、3次元球面は、3次元の閉じた空間になっており、3次元的な境界は
存在しません。
ちなみに、w=-1 から w=0 までの3次元球面の各断面は、例えば、w=b(-1<b<0)にある半径Rの球体を、w=-1 から w=0 までの
4次元空間内に引き伸ばしたものの断面、と考えることができます。同様に、w=0 から w=1 までの3次元球面の各断面は、例えば、
w=c(0<c<1)にある半径Rの球体を、w=0 から w=1 までの4次元空間内に引き伸ばしたものの断面、と考えることができます。
すなわち、球体を4次元空間内で引き伸ばしたものを2つ用意して、例えば、w=0 において、球体の表面どうしを貼り合せると、3次元球面が
出来上がることがわかります。
なお、3次元球面の基本群(1次元ホモトピー群)は、位数1の自明な群となります。すなわち、3次元球面の中にある任意のループは、必ず
1点にまで収縮させることが出来ます。
また、3次元球面は、向き付け可能な3次元多様体です。したがって、例えば、正四面体を3次元球面の中でどのように移動したとしても、
正四面体の向きが変化することはありません。ちなみに、向き付け不可能な3次元多様体の中で正四面体を移動させると、元の正四面体と
その鏡像対称体の区別が付かなくなります(→ 『ギーゼキング多様体 と レンズ空間』 参照)。
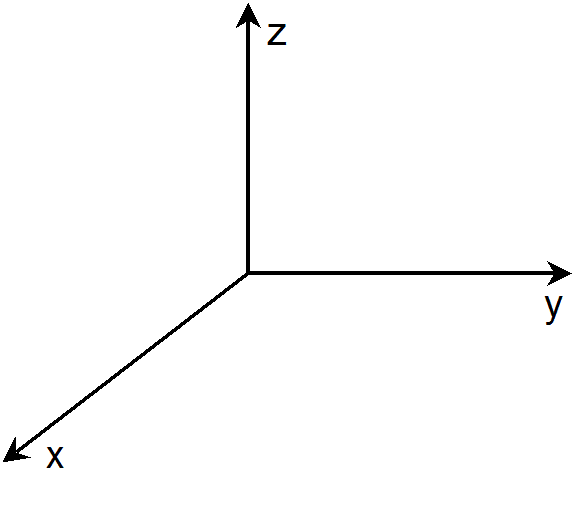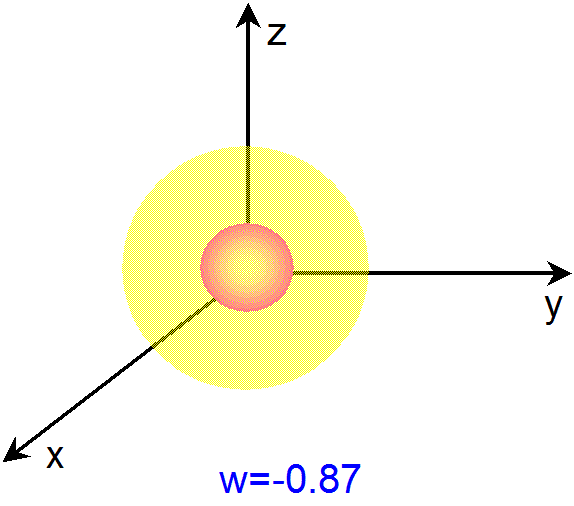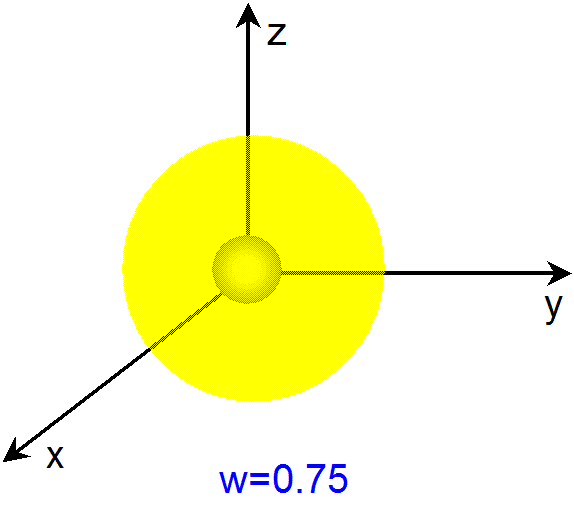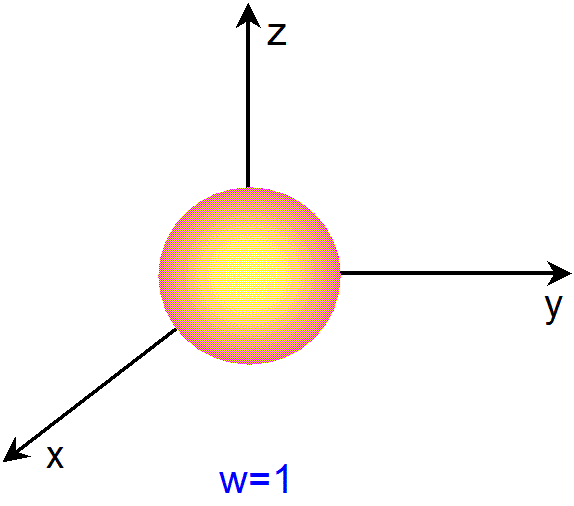
3次元球面と同様に、S2XS1 多様体のGIFアニメーション(GIF animation)も作ってみました。
右のアニメーションです。
まず、S2XS1 多様体とは、3次元球面や3次元トーラスと同様、3次元閉多様体の
一種です。
3次元球面はS3、3次元トーラスは
S1XS1XS1 と表せる様に、
S2XS1 多様体はS2XS1 と表せます。
ここで、X は、直積を意味します。この直積での表現からわかるように、S2XS1 多様体は、
3次元球面と3次元トーラスの中間的な多様体です。
では、このアニメーションを使って、S2XS1 多様体を説明します。まず、w=-1 や w=1 での
S2XS1 多様体の断面は、半径R1の球面、です。また、w=0 でのS2XS1 多様体
の断面は、半径R0 の球面(ピンク色の球面)と半径R2 の球面(黄色の球面)です。なお、図(アニメ)からわかるように、
R0<R1<R2 と言う大小関係になっています。そして、w=a(-1<a<0、0<a<1)での
S2XS1 多様体の断面は、半径Rg の球面(ピンク色の球面、R0<Rg<R1 )
と半径Rh の球面(黄色の球面、R1<Rh<R2 )です。
w=-1 から w=0 までのS2XS1 多様体の各断面は、例えば、w=b(-1<b<0)にある半径R2 の球体に対して、
その中心に近い半径R0 の球体部分を刳り貫いて、w=-1 から w=0 までの4次元空間内に引き伸ばしたものの断面、と考えることが
できます。同様に、w=0 から w=1 までのS2XS1 多様体の各断面は、例えば、w=c(0<c<1)にある半径R2
の球体に対して、その中心に近い半径R0 の球体部分を刳り貫いて、w=0 から w=1 までの4次元空間内に引き伸ばしたものの断面、
と考えることができます。
すなわち、中心部分を刳り貫いた球体(中空球体)を4次元空間内で引き伸ばしたものを2つ用意して、例えば、w=0 において、中空球体の
外側の表面どうし、内側の表面どうしを、それぞれ貼り合せると、S2XS1 多様体が出来上がることがわかります。
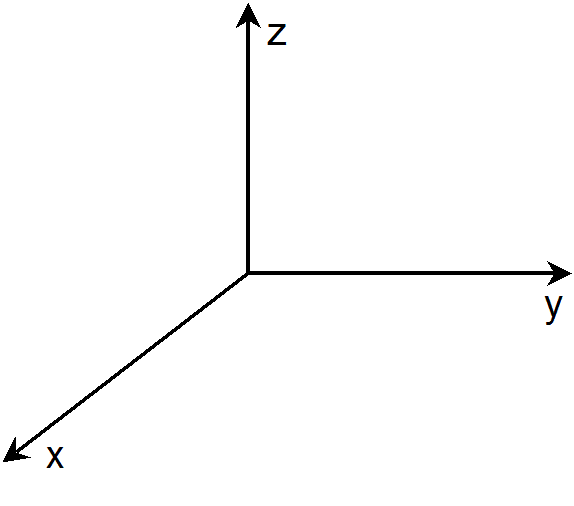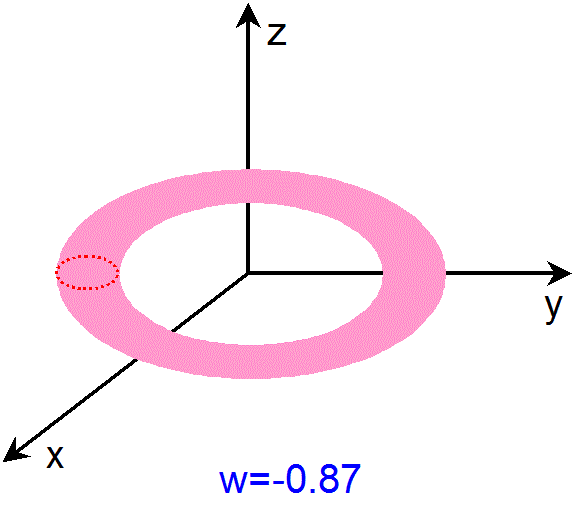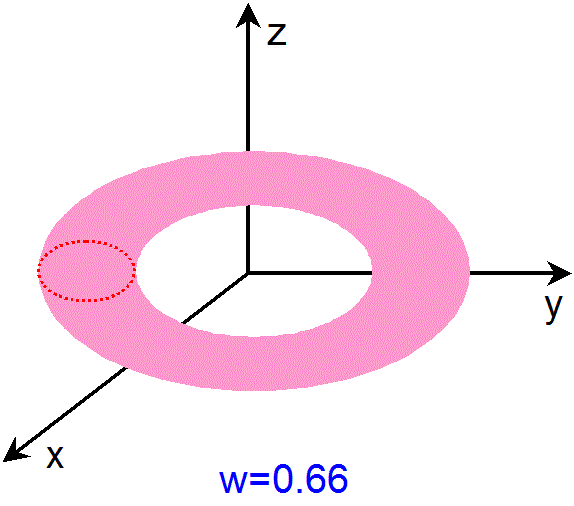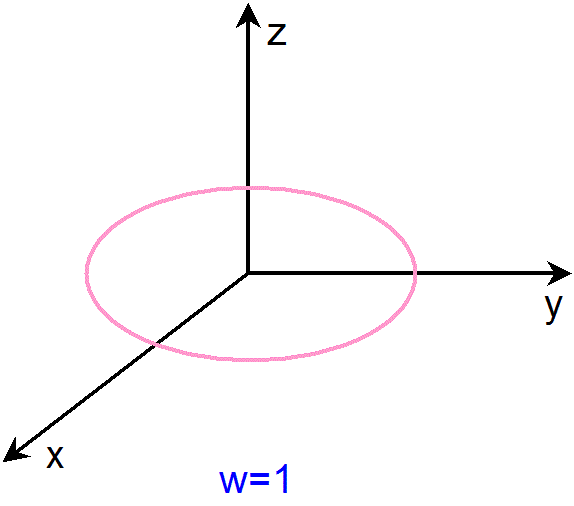
S2XS1 多様体のGIFアニメーション(GIF animation)を、もう1つ、作りました。
右のアニメーションです。
S2XS1 多様体は、その4次元空間内への収め方を変えることで、1つ目のアニメーション(右上)の様に表せたり、
2つ目のアニメーション(右)の様に表せたりします。2つのアニメーションは、一見、全く違うように見えます。しかし、良く見ると、ともに、
S2XS1多様体を表していることがわかります。
そして、2つ目のアニメーション(右)からは、次のことがわかります。
w=-1 から w=0 までのS2XS1 多様体の各断面は、トーラス体を、w=-1 から w=0 までの4次元空間内に引き伸ばした
ものの断面、と考えることができます。同様に、w=0 から w=1 までのS2XS1 多様体の各断面も、トーラス体を、w=0
から w=1 までの4次元空間内に引き伸ばしたものの断面、と考えることができます。
すなわち、トーラス体を2つ用意して、w=0 において、その表面どうしを貼り合せると、S2XS1 多様体が出来上がる
ことがわかります。
ちなみに、S2XS1 多様体は、レンズ空間 L(0,1) でもあり、その基本群は Z={ 0, ±1, ±2, ±3, ・・・ } : 整数
全体の加法群 となります。
ところで、3次元球面は、2つの球体の貼り合わせだけでなく、2つのトーラス体の貼り合わせでも、作ることが出来ます。( 『
閉曲面の裏返し と 3次元球面 』 を、ご参照ください。)
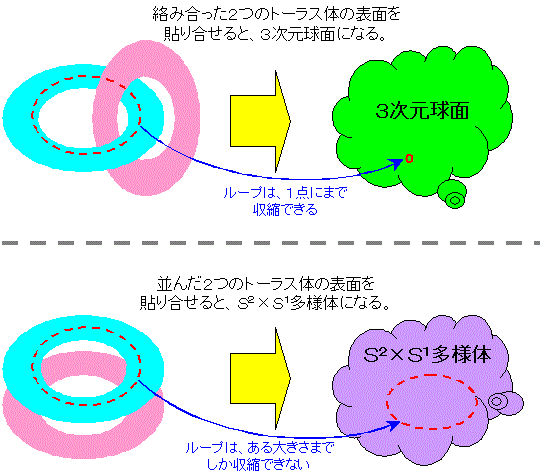
具体的に言うと、右の図の上側のように、絡み合った2つのトーラス体の表面どうしの貼り合せで、3次元球面が実現できます。
また、トーラス体の内部を一回りするループ(右の図の上側の赤いループ)は、この貼り合わせを行う前は、当然ながら、1点にまで収縮させることは
出来ません。しかし、絡み合った2つのトーラス体の貼り合わせの後、このループを1点にまで収縮させることが出来ます。なぜなら、このような
貼り合わせを行うと、2つのトーラス体は、互いに相手の穴を埋め尽くして、穴が無くなるからです。すなわち、貼り合わせた後は、3次元球面に
なるのです。
一方、既に、S2XS1 多様体の2つ目のアニメーションを説明する所で述べましたように、
S2XS1 多様体も、3次元球面と同じく、2つのトーラス体の貼り合わせにより、作ることが出来ます。
しかし、3次元球面を作る場合とは、貼り合わせ方が異なります。具体的に言うと、右の図の下側のように、並んだ2つのトーラス体の表面どうしを
貼り合せると、S2XS1 多様体が実現できます。
なお、トーラス体の内部を一回りするループ(右の図の下側の赤いループ)は、貼り合わせの後も、ある大きさのループまでしか、
収縮できません。なぜなら、トーラス体の穴は、貼り合わせた後も、4次元空間内の穴として、引き継がれているからです。