ポアンカレ球面・ザイフェルトウェーバー多様体 etc.
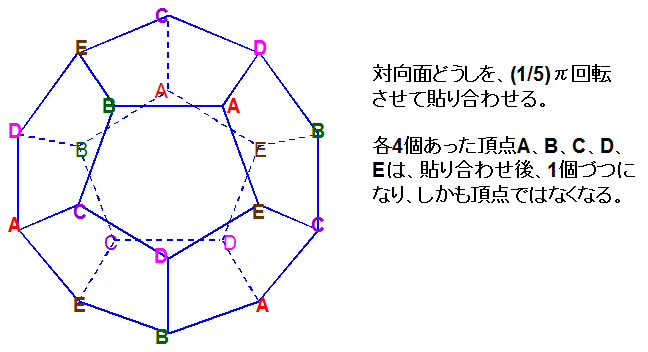ポアンカレ球面（ポアンカレホモロジー球面）は、正12面体の向かい合う面どうしを右図のように貼り合わせることで得られる
閉３次元多様体です。
この多様体のホモロジー群は３次元球面と同じですが、その基本群（１次元ホモトピー群）は、３次元球面の場合のような位数１の自明な群ではなく、
位数120の2項正20面体群（binary icosahedral group）となります。
なお、右図の右側に付記したように、頂点の個数は貼り合わせをすることで４分の１になるから、貼り合わせ後は４つの頂点立体角が１つの点を
囲むことになります。また、正十二面体の頂点立体角は、3cos-1(-1/51/2)−π≒2.96174 (sr) です。よって、１つの点を
囲む４つの頂点立体角の和は、2.96174×4≒11.8＜12.6≒4π (sr) となります。すなわち、頂点立体角の和が 4π (sr) より小さいことから、
ポアンカレ球面は、S3等 の一種であることがわかります。
参考資料： ・下記の各URL
http://infoshako.sk.tsukuba.ac.jp/~hachi/math/library/poincare.html
http://math.a.la9.jp/aumer.htm
http://shironetsu.hatenadiary.com/entry/2018/03/31/142224
・Wikipedia 『Seifelt-Weber space』、『Homology sphere』、『立体角』
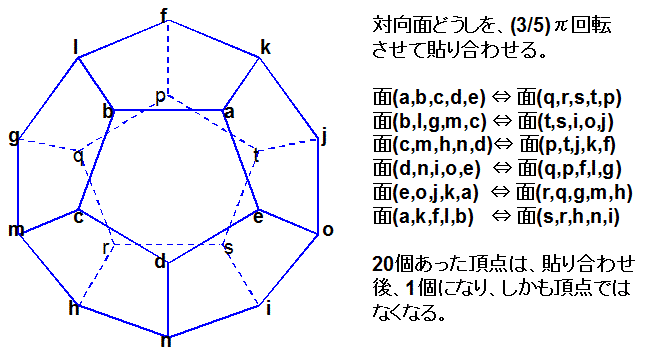ザイフェルトウェーバー多様体は、正12面体の向かい合う面どうしを右図のように貼り合わせることで得られる閉３次元多様体で、
３次元双曲多様体の一種です。
なお、右図の右側に付記したように、頂点の個数は貼り合わせをすることで２０分の１になるから、貼り合わせ後は２０個の頂点立体角が１つの点を
囲むことになります。また、正十二面体の頂点立体角は、3cos-1(-1/51/2)−π≒2.96174 (sr) です。よって、１つの点を
囲む２０個の頂点立体角の和は、2.96174×20≒59.2＞12.6≒4π (sr) となります。すなわち、頂点立体角の和が 4π (sr) より大きいことから、
ザイフェルトウェーバー多様体は、H3 の一種であることがわかります。
参考資料： ・下記URLに掲載のPDFファイル
http://ir.c.chuo-u.ac.jp/repository/search/binary/p/2249/s/2215/
・Wikipedia 『Seifelt-Weber space』、『立体角』
・下記URL
http://math.a.la9.jp/aumer.htm
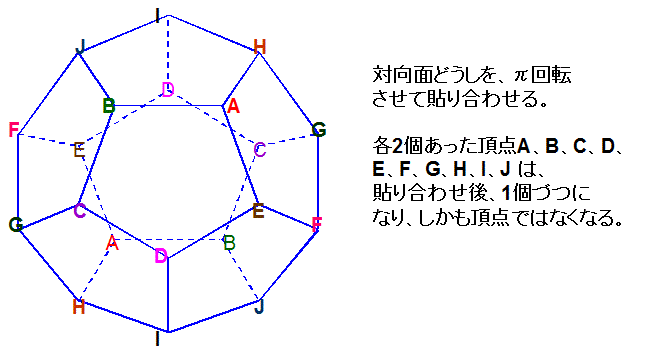正12面体の向かい合う面どうしを右図のように貼り合わせると、３次元実射影空間（RP3）が得られます。
なぜかと言うと、右図をよく見るとわかりますが、この多様体は、正12面体の中心に対して対称な点どうしを貼り合わせたものだからです。
なお、３次元実射影空間をより簡単にイメージするには、正12面体ではなく球体の方が良いでしょう。すなわち、球体の中心に対して対称な
球面上の点どうしを貼り合わせれば、３次元実射影空間が得られます。
なお、右図の右側に付記したように、頂点の個数は貼り合わせをすることで２分の１になるから、貼り合わせ後は２つの頂点立体角が１つの点を
囲むことになります。また、正十二面体の頂点立体角は、3cos-1(-1/51/2)−π≒2.96174 (sr) です。よって、１つの点を
囲む２つの頂点立体角の和は、2.96174×2≒5.9＜12.6≒4π (sr) となります。すなわち、頂点立体角の和が 4π (sr) より小さいことから、
３次元実射影空間は、S3等 の一種であることがわかります。
参考までに、射影平面（２次元実射影空間）は向き付け不可能な多様体ですが、３次元実射影空間は向き付け可能な多様体です。また、３次元
実射影空間（RP3）は、レンズ空間の一種で、L(2,1) と言う記号で表される多様体です。
参考資料： ・Wikipedia 『Seifelt-Weber space』、『射影空間』、『立体角』
・下記URL
http://math.a.la9.jp/aumer.htm
