| HOME | ソフトウェア | オーダーメイド地図 | 地図投影法 | 地図の歴史 | 世界の国々 | 用語集 | 地理リンク集 | メッセージ |
| 用語集 |
ある特定の主題(テーマ)に合わせて作成した地図のことを「主題図」といいます。「一般図」(地形図、市街図)に対する用語です。人工分布図、地質図、気候図、土地利用図、など地理的な広がりを持つ情報なら、ほとんど何でも主題図にすることが可能です。PTOLEMYは主題図用のベースマップを生成するツールです。
球と平面の交差の仕方をあらわすことばです。平面が球の中心を通るときに、球と平面が交差してできる円が大円です。地球でいえば赤道や経線(子午線)、さらに大圏コースが大円になります。
球と平面の交差の仕方をあらわすことばです。平面が球の中心を通らないときに、球と平面が交差してできる円が小円です。地球でいえば赤道以外の緯線は小円です。
地図の中で正しい長さで表現されている線のことを「等長線」あるいは「標準線」いいます。経線が等長線である図法、緯線が等長線である図法、特定の2地点を結ぶ線が等長線である図法、等長線が存在しない図法、などいろいろあります。また等長線が1本だけの図法、すべての経線が等長線である図法など、数もまちまちです。投射図法であれば接線は必ず等長線になります。そのため円錐図法のように等長線が弧で表わされる図法もあります。地図の縮尺は等長線の縮尺を示しているため、地図上で距離を計測するときは、どこが等長線であるか知っておく必要があります。
投影面と地表面の接線あるいは割線は伸び縮みがなく正しい長さで表わされます。正軸法では接線が緯線と一致するため、この緯線を「標準緯線」といいます。標準緯線の数は、投影面と地表面が接する接図法では1本、投影面が地表面に潜り込む割図法では2本になります。
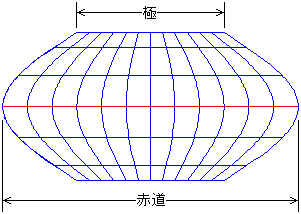
| 円筒図法では極が赤道と同じ長さの直線で表わされるため面積のひずみが大きくなってしまいます。これを解消するために極を点で表わすモルワイデ図法のような図法もありますが、今度は縁辺部での傾斜がきつくなり形状のひずみが大きくなってしまいます。平極法は両者の欠点を克服するために考案された図法で、極を赤道の半分の長さの直線で表わし、全体の形状がタル型になります。 |
 |
| 経線が極に収束するタイプの擬円筒図法では、中央経線から離れた高緯度の地域で角度のひずみが大きくなります。しかし経線にそっていくつかの切れ目を入れ、各ブロックごとに収束させれば大幅にひずみを減らすことができます。これが「断裂法」です。舟型多円錐図法も断裂図法の一種ですが、ここではグード図法で考案された断裂処理を説明します。 切れ目はどこに入れてもよいのですが、一般的には海洋に数本の切れ目を入れて大陸のひずみを小さくします。海洋に注目したいときは大陸に切れ目を入れることもあります。PTOLEMYでは下の図のように、東経0度、北緯0度を中心にして、北半球を2つの部分、南半球を4つの部分に分けています。ただしグリーンランドが分かれないようにする処理はおこなっていません。 断裂処理を擬円筒図法に対するオプションとする方法も考えられますが、PTOLEMYではグード図法でのみおこないます。 |
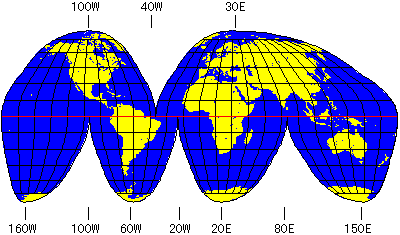 (図:切れ目と各部分の中央経線の経度) |
フランドル地方のアントワープ近郊出身の地理学者。地図工房を持ち、パレスチナやフランドルの地図作成から始まり、1538年に制作した世界図では新大陸に対して初めて“アメリカ”と記述しました。1569年には航程線(等角航路)を直線で表すことができ現在も広く使われる、メルカトル図法を考案して世界図を出版しました。さらに彼の死後1602年に出版された世界地図帳のタイトル『アトラス』は、地図帳の代名詞となりました。
ドイツのミュールハウゼンに生まれ、物理学や数学の分野に多くの功績を残すが、1772年からは数学者としての能力を地図投影法の研究に活かし、多くの図法を考案しました。ランベルト正積方位図法、ランベルト正角円錐図法、ランベルト正積円錐図法、ランベルト正積円筒図法などがあります。
エジプトのアレクサンドラで活躍したギリシア人の天文・地理学者。天文学では古代天文学の集大成『アルマゲスト』を著し、地理学でもやはり集大成である『地理学』を著しています。これにはあらゆる地理知識が集められ、一種の正距円錐図法による世界図も添えられています。ルネサンス期にいたるまで科学的な地図学の基礎となる書物です。