Top page (correct Bohr model including the two-electron atoms)
Quantum Hall effect by realistic de Broglie wave
What is the true meaning of Planck constant.
Quantum Hall effect is observed in two-dimensional electron systems subjected to low temperatures and strong magnatic fields, in which Hall conductivity σ takes the quantized values (= n e2/h ).
This includes Planck constant, so it is used for determining Planck constant.
And the quantum Hall effect is important for the definition of a new standard for electrical resistance.
By the way, what on earth is this quantum Hall effect ?
And what does the Planck constant h of this effect really mean ?
In this page, we try to find the concrete image and the true meaning of the quantum Hall effect ( see also this page ).
Quantum Hall effect uses the two-dimensional electron (hole gas) systems, in which moving electrons are confined to only one plane.
To achieve this condition, we take the interface between a semiconductor and other material.
Semiconductor has the properties between conductor and insulator, and has discrete band energies.
Gaps between band energies are smaller than insulator, so it can act like a conductor, too.
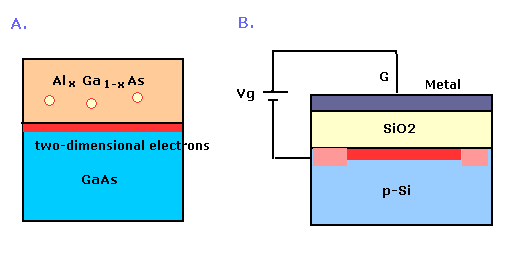
(Fig.1)

A of Fig.1 is heterojunction of III-V compounds of the semiconductor GaAs / Alx Ga1-x As.
AlGaAs (upper layer) supplies electrons (= donor ) to the lower layer.
And these electrons are pulled back to the upper layer by the attractive Coulomb force.
As a result, these electrons are trapped between these two layers. (red part).
B of Fig.1 is the metal-oxide-semiconductor (MOS) structure.
The Mos device is fabricated from moderately- doped p-type (blue) or n-type (pink) silicon.
There are an insulating layer of silicon dioxide and a metal layer above the two-dimensional electron's layer (red).
The enegy levels are discrete vertically, so the moving electrons are confined to the red layer.
Vg is called "gate voltage".
As the Vg becomes bigger, more electrons enter the red layer, so it causes the increased electric current (and conductivity) in the red plane.
First, we calculate the number of electrons per unit area in the quantum mechanical way.
The Schrodinger equation of the electron in the x-y plane is
(Eq.1)
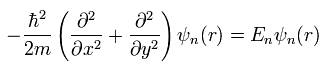
Here we suppose the electron is confined to the regular square that has a side length L.
The periodic boundary condition is
(Eq.2)
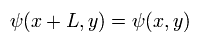
Using the wave number vector (k), the wave function (ψ) is expressed as
(Eq.3)
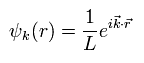
From Eq.2, the x and y components of the wave number become
(Eq.4)
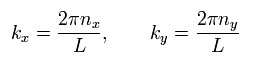
where nx and ny are an integers.
So this means the wavelength (λ) is quantized.
From de Broglie's relation, the kinetic energy of the electron is
(Eq.5)
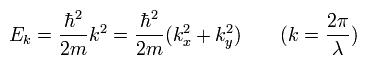
Fermi energy (EF) can be expressed using the Fermi wavenumber kF
(Eq.6)
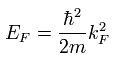
In the semiconductor or insulator, the band structure is formed, in which the electrons are arranged from the lowest energy level in order.
The highest energy level that has electrons is called "Fermi energy".
(Caution: this quantum mechanical world is too "mathematical" to imagine concretely.)
The volume element of the two-dimensional wave space is (2π / L)2.
The total number of the states which are allowed in the Fermi circle (πkF2) is expressed as
(Eq.7)
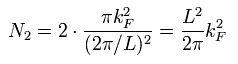
where we consider the degree of freedom by spin (= 2).
From Eq.7, the electron's number per unit area is
(Eq.8)
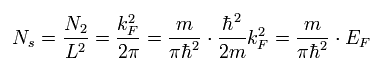
(Caution; this result doesn't change, if we suppose L=1 from the beginning. )
But in fact, the "mathematical" result of Eq.8 is a little different from the real world.
The enectron number density by Eq.7 and Eq.8 doesn't consider the differences of the "actual" area in each wave number.
According to the Lorentz force, the Landau orbital radius is bigger, as the energy levels is higher.
So we have to think about the "actual area" in addition to the number of states, when we derive the electron's density.
Next we consider the electron's motion under the electromagnetic field.
The electrons are moving around in the x-y plane, and the magnetic field (B) is in the z direction.
(Fig.2)
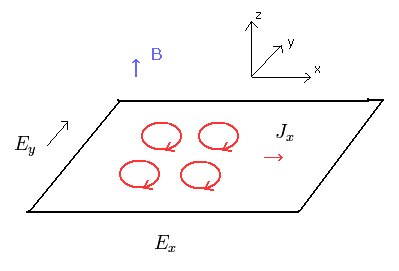
From Lorentz force and Coulomb force, the equation of motion becomes
(Eq.9)
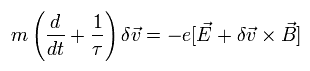
where δv means the electron's velocity in the space of the wavefunction.
(Quantum mechanically, it is a little difficult to imagine. But classically, it is very easy.)
m, E, and B mean the electron's mass, electric field, and magnetic flux density, respectively.
τ of the left side in Eq.9 means the relaxation time of the scattering.
As this τ becomes longer, the electron is not scattered by other things.
(As τ becomes longer, the "friction" by scattering becomes smaller.)
Considering the magnetic field (B) is the z direction (0, 0, +B), the x and y components of the electron's motion are.
(Eq.10)
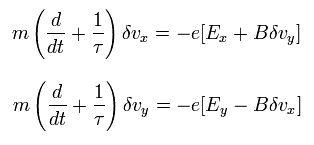
In the stationary state, the time derivative of δv becomes zero, as follows,
(Eq.11)
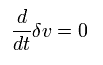
Under the magnetic field, the electron moves circularly.
Supposing the centrifugal force is equal to the Lorentz force, the angular frequency (ω) becomes
(Eq.12)
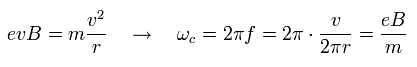
From Eq.11 and Eq.12, Eq.10 becomes
(Eq.13)
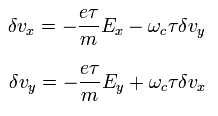
Solving Eq.13, the x and y components of the velocity are
(Eq.14)
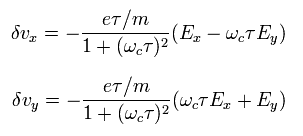
Here we define σ0, as follows,
(Eq.15)
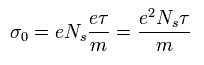
where Ns means the electron's number per unit area.
Using Eq.14 and Eq.15, the current density ( J = -eNsv ) is
(Eq.16)
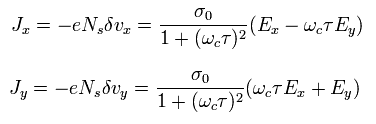
Eq.16 can be expressed using the electrical conductivity tensor, as follows,
(Eq.17)
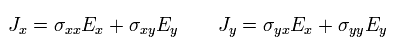
As the electrical conductivity is bigger, more electrons can flow.
From Eq.16 and Eq.17,
(Eq.18)
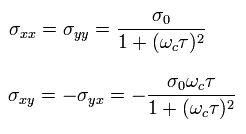
σxy of Eq.18 can be changed as follows,
(Eq.19)
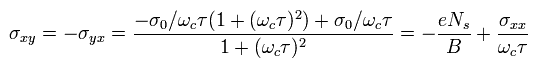
Using the inverse matrix, Eq.17 can be expressed as
(Eq.20)
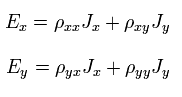
where ρ means electrical resistivity. (ρ = R = resistance.)
According to the formula of the inverse matrix, each ρ is
(Eq.21)
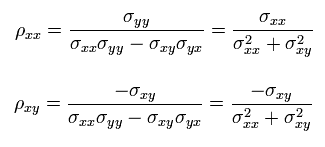
From Eq.12, Eq.15, Eq.18 and Eq.21,
(Eq.22)
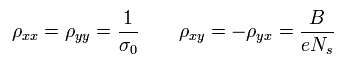
Under the strong magnetic field, electrons in the two dimensional system, are moving circularly by Lorentz force.
(cyclotron movement)
The angular frequency of this cyclotron movement is Eq.12.
According to the quantum mechanical harmonic oscillator, the energy of this electron is quantized, as follows,
(Eq.23)
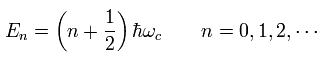
Eq.23 is called "Landau level", and n is called "Landau index".
And the Landau orbital radius is
(Eq.24)
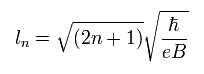
As you notice, these methods contains both the classical and quantum mechanical concepts.
So it is very difficult to imagine.
Forgetting spin effect in Eq.8, the number of states included in the Landau levels (from zero to n) becomes,
(Eq.25)
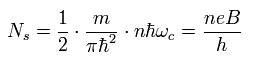
Again, this is difficult to imagine.
( If the electrons exist from 0 to n energy levels, why don't we use ( 1 + 2 + 3+ ... + n ) instead of only n ? )
Next we explain the concrete image of these movement.
The electron is rotating around in the x-y plane by Lorentz force under the magnetic field B in the z direction.
(Fig.3)
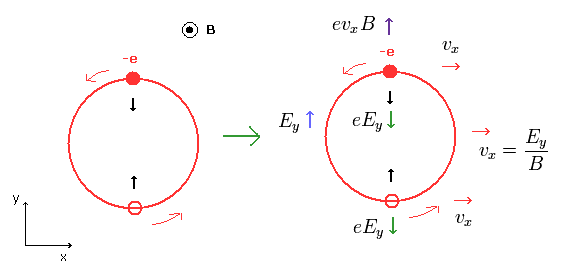
When the electric field ( Ey ) is applied in the y direction, the whole electron's circle moves in the x direction, as shown in Fig.3.
When the electron is moving in the x direction, Lorentz force by this movement is equal to that of the electric field, as follows,
(Eq.26)
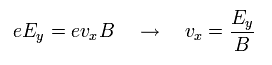
From Eq.26, the electric current density (J) in the x direction becomes
(Eq.27)
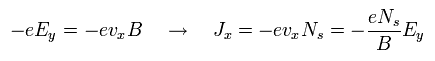
where Ns is the number density.
From Eq.17, Eq.25 and Eq.27, the Hall conductivity ( σxy ) becomes
(Eq.28)
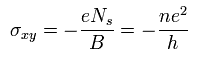
As a result, Hall conductivity is quantized !
n of Eq.28 is called "Landau filling factor."
And h/e2 is called von Klitzing constant Rk (Ω).
When Eq.27 and Eq.28 are satisfied, the friction is zero.
(The relaxation time τ of the scattering is infinite. See Eq.19.)
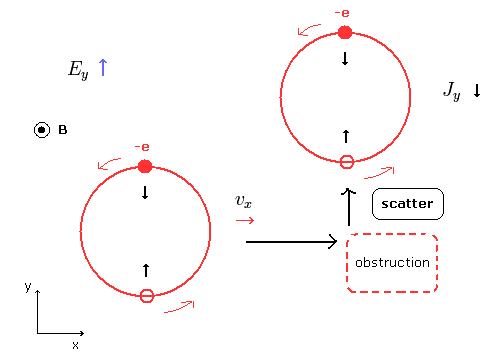
By the way, how is the electric current in the y direction excited by the electric field of Ey ?
This current under the magnetic field is caused by the scattering of the electrons, as shown in Fig.4.
(Fig.4)
As shown in Eq.15, Eq.18 and Eq.22, the diagonal resistance (ρxx) and diagonal conductivity (σxx) become smaller, as the relaxation time τ is longer.
(Eq.29)
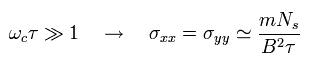
(Eq.30)
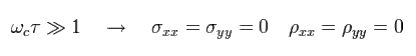
This means the diagonal resistance is related to the scattering of the electrons.
So when the diagonal resistance (ρxx) is not zero, the Hall conductivity σxy (or Hall resistance ρxy ) is not quantized.
But later research had proved that n of Eq.28 includes not only integers but also fractions.
This means that the above hypothesis using Landau filling factor n is incomplete.
We need another explanation.
(The fraction is thought to be caused by the electron-electron interactions. But the mechanism of it is not understood well.)
Some people try to introduce strange concept of "anyons", which are neither bosons nor fermions.
Anyon has "fractional" charge (= 1/m e ). But does this strange thing really exist ?
Instead, we try to explain the fractional quantum Hall effect naturally, using Bohr's de Broglie waves.
Here we use the Bohr-Sommerfeld quantization condition, in which the electron's orbital length is an integer times de Broglie's waves.
So the next two conditions need to be satisfied.
(Eq.31)
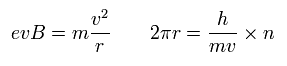
The first equation means that the centrifugal force is equal to Lorentz force.
Solving Eq.31, we get
(Eq.32)
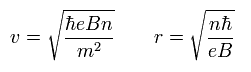
From Eq.32, the area of the circle is
(Eq.33)
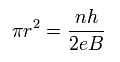
And the kinetic energy of the electrons is
(Eq.34)
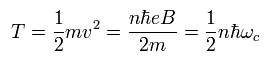
where we use Eq.12 of
(Eq.12)
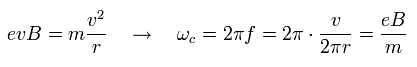
In addition to the kinetic energy, we have to consider the magnetic energy in the real world.
The magnetic moment is the current (I) × area, as follows,
(Eq.35)
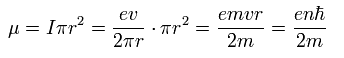
So the magnetic energy under the magnetic field B is
(Eq.36)
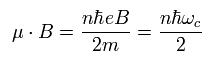
where the directions of the magnetic moment and magnetic field are opposite, so its interaction energy become "positive".
Summing Eq.34 and Eq.36,
(Eq.37)
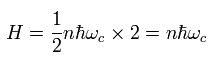
This result is almost same as the Landau energy level of Eq.23.
So we can express Landau energy level "classically" (+ de Broglie waves.)
Here we suppose the k electrons are included in the orbit with the area of Eq.33.
Using Eq.26 and Eq.33, the electric current density (Jx) in the x direction by the electric field Ey is
(Eq.38)
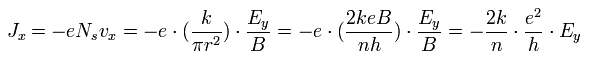
From Eq.38, the Hall conductivity σxy is
(Eq.39)
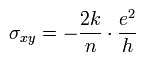
Eq.39 means the fractional quantum Hall effect !
(Compare Eq.39 and Eq.28.)
Due to the factor "2" of the numerator of Eq.39, the denominator of the irreducible fraction of Eq.39 tends to be "odd" number.
And in this case, the Hall resistance ρxy is
(Eq.40)
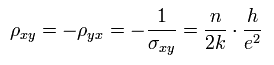
As I said, the diagonal resistance is related to the scattering of the electrons.
So when the diagonal resistance (ρxx) is zero, the Hall conductivity σxy (or Hall resistance ρxy ) is quantized (= fractional ).
(Fig.5) Expetimental result.
Multiplying E and J by the length l,
(Eq.41)
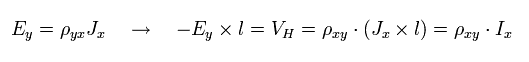
where VH and I mean the voltage and current, respectively.
So the (Hall) resistance is equal to ρxy, as follows,
(Eq.42)
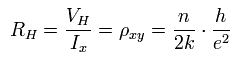
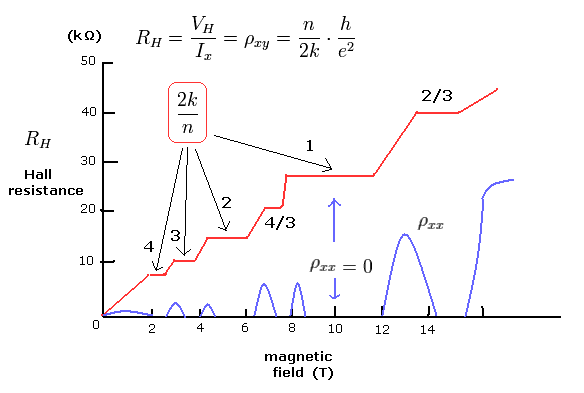
What is a concrete state of each 2k/n of Eq.39 ?
In Eq.39, n means the number of de Broglie waves of the orbit, and k means the number of the electrons included.
First, we think about 2k/n = 1. (See also Fig.5.)
(This case corresponds to n=1 of Eq.28. So "integer" quantum Hall effect.)
For example, one orbit of 2 × de Broglie wavelength (n=2) contains one electron (k=1). (Fig.6.)
(Fig.6) One example of 2k/n = 1.
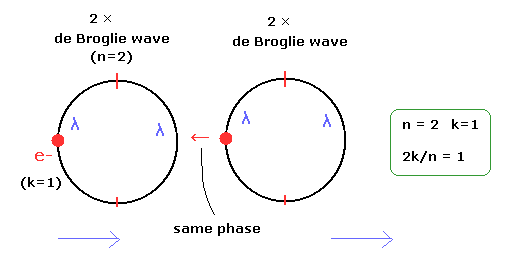
If only 1 × de Broglie wavelength orbits exist in the plane, the opposite wave phases of the adjacent orbits cancel each other.
So the electron's motion becomes unstable and they are thought to be scattered.
---------------------------------------------------
When the orbital length is 1 × de Broglie's wave, the magnetic moment by this electron's motion becomes "Bohr magneton".
And this Bohr magneton is the same as the spin magnetic moment.
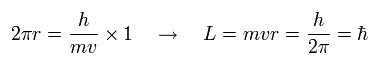
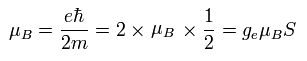
Lorentz force causes the magnetic moment, which direction is opposite from that of the magnetic field (B).
To be in stable and lower energy, the direction of the magnetic moment needs to be same as that of the magnetic field.
So the direction of this Bohr magneton is thought to be "oscillating".
-----------------------------------------------------
In the case of Fig.6, the same wave phases of adjacent 2 × de Broglie wavelength orbits interfere with each other, and they can stick to each other.
Next we consider 2k/n = 2.
(This case corresponds to n=2 of Eq.28.)
For example, an orbit of 2 × de Broglie wavelength (n=2) contains one electron.
And furthermore an orbit of 1 × de Broglie wavelength with one electron is included in it. (Fig.7).
( As a result, k= 1+1 = 2).
(Fig.7) One example of 2k/n = 2.
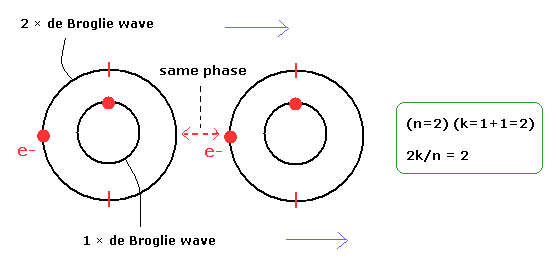
According to Eq.26, the velocities in the x direction of these orbits are the same.
Next we consider 2k/n = 3.
(This case corresponds to n=3 of Eq.28.)
For example, an orbit of 4 × de Broglie wavelength (n=4) contains two electrons.
And furthermore an orbit of 3 × de Broglie wavelength with two electrons and an orbit of 2 × de Broglie wavelength with two electrons are included in it. (Fig.8).
( As a result, k= 2+2+2 = 6).
(Fig.8) One example of 2k/n = 3.
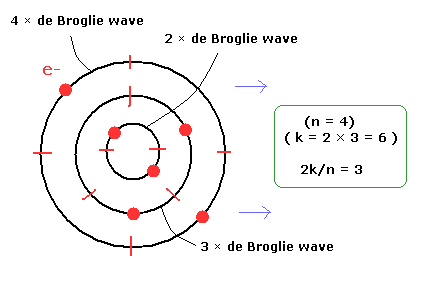
According to Eq.26, the velocities in the x direction of these orbits are the same.
As shown in Fig.5, the magnetic field in the case of 2k/n = 3 is weaker than those of 1 and 2.
The orbital radius of Eq.32 is bigger, as the magnetic field is weaker.
So the repulsive force between electrons are weaker, which tends to allow overlapping of some different orbits.
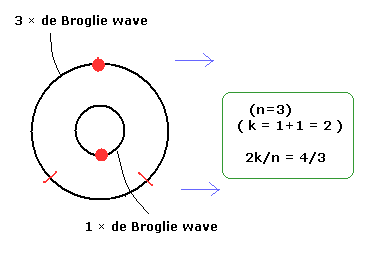
Next we consider 2k/n = 4/3.
(This case corresponds to n= 4/3 of Eq.28. So the fractional quantum Hall effect.)
For example, an orbit of 3 × de Broglie wavelength (n=3) contains one electron.
And furthermore an orbit of 1 × de Broglie wavelength with one electron is included in it. (Fig.9).
( As a result, k= 1+1 = 2).
(Fig.9) One example of 2k/n = 4/3.
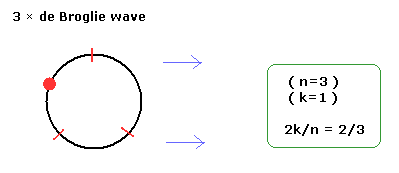
Next we consider 2k/n = 2/3.
(This case corresponds to n= 2/3 of Eq.28. So the fractional quantum Hall effect.)
For example, an orbit of 3 × de Broglie wavelength (n=3) contains one electron.
( As a result, k= 1).
(Fig.10) One example of 2k/n = 2/3.
As shown in Eq.32, the orbital radius becomes smaller, as the magnetic field (B) is stronger.
So the radius of Fig.10 is smaller comparing Fig.9 in the same n =3 orbits.
The repulsive forces between electrons become stronger in Fig.10.
As a result, it is more difficult that the small n=1 or n=2 orbits contain electrons.
By these mechanism, we can explain why the Hall resistance becomes bigger, as the magnetic field is stronger.

2011/6/27 updated. Feel free to link to this site.