トップページ (2電子原子も含む正確な新ボーア模型)
量子電磁力学の異常磁気能率。
特殊相対論は間違っている。
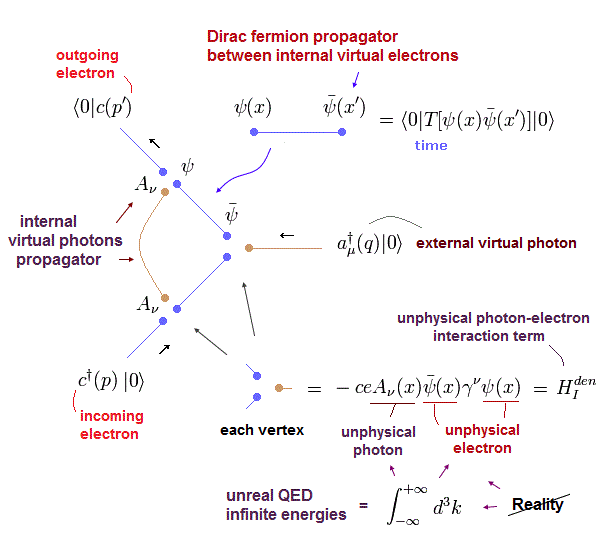
(Fig.1) 内線 = 伝播関数。

伝播関数は 量子電子力学 ( QED ) において 様々な値を計算する 主要なツールである。
QED の伝播関数は 古典的なローレンツ力を 相対論的な相互作用に変換することによって 導入された。
これはつまり 特殊相対論が間違っているとしたら、伝播関数を用いたこれらの相互作用も間違いということになる。
このセクションでは、様々な場 ( スカラー、ディラック、電磁場 ) における ファインマン伝播関数について説明する。
伝播関数について理解するには、最初に 基礎的な場の量子論について理解する必要がある。
そのため まだ読まれてないようなら このページを最初に読むように。
実クライン・ゴルドン場の平面波解は
(Eq.1)
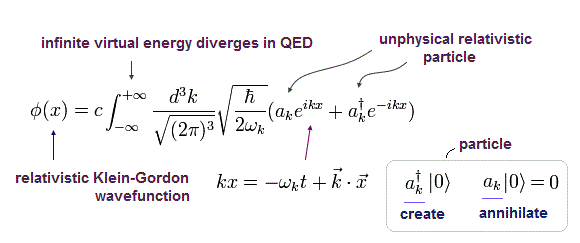
ここでは (-1, 1, 1, 1) バージョンの計量テンソルを使用している。
(1, -1, -1, -1) バージョンに変更したいときは、 ( kx → -kx, k2 → -k2 ) のように表記を変更するように。
意味はかわらず、表記法のみ異なるだけである。
( 付録 も参照のこと。 )
スカラー場の 伝播関数 ( グリーン関数 ) は 次のように表される。
(Eq.2)

ここで θ(t-t') は ヘヴィサイドの階段関数である。
(Eq.3)
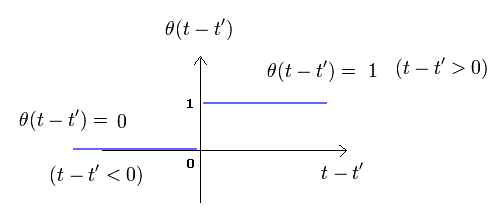
これは 時間順序を表すのに使用される。
Eq.3 の階段関数 (= θ ) は、 (t-t') が正のとき、 θ は "1"。 t-t' が負のとき、 θ は ゼロになる。
Eq.2 は スカラー粒子が 真空から まず生成された後、消滅することを意味している。
( Eq.1 は "生成" ( a† ) と "消滅" ( a ) 演算子を含んでいる。 )
もちろん、Eq.1 に示すように、伝播関数は 無限種類の運動量 ( ħ k ) の 無限の粒子 を含んでいる。
( つまり、伝播関数自体は 実在のものではない。しかし QED は この概念を計算値を得るのに使用している。)
複素積分を使用すると、階段関数は 次のように表される。
(Eq.4)
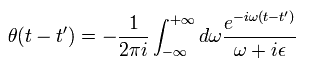
と
(Eq.5)
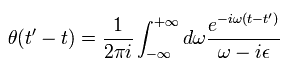
ここでは 指数関数部分を同じにしてある。
--------------------------------------------------
最初に Eq.4 を証明する。
この証明をスキップしたいときは、次のセクションに進まれるように。
Eq.4 を証明するには、コーシーの留数定理を用いなければならない。
留数定理では、1/(z-a) の係数のみ 複素積分によって残る。
(Eq.6)
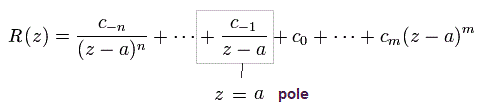 と
と
(Eq.7)
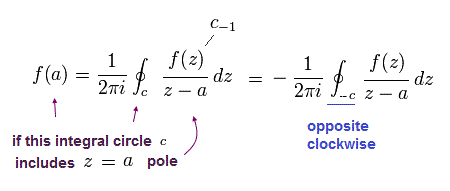
ここで 積分は 反時計回りの閉曲線である。
閉曲線が "極" を含んでいないとき、Eq.7 はゼロになる。
(Eq.4)
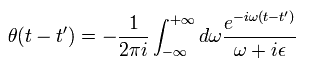
Eq.4 では、t-t' が 正 ( t-t' > 0 ) のとき、 Eq.4 の指数関数は 次のように ω = -i∞ の部分でゼロになる。
(Eq.8)
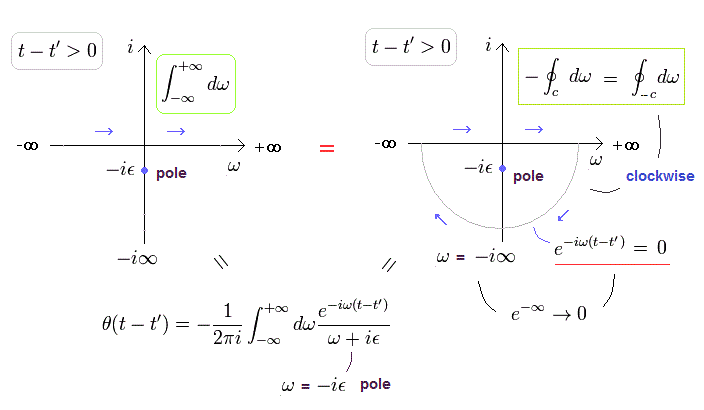
そのため 実数線沿いの -∞ から +∞ の積分を Fig.2 に示す 複素積分と同様に見なせる。
(Fig.2) Eq.4 の階段関数 ( t-t' > 0 )
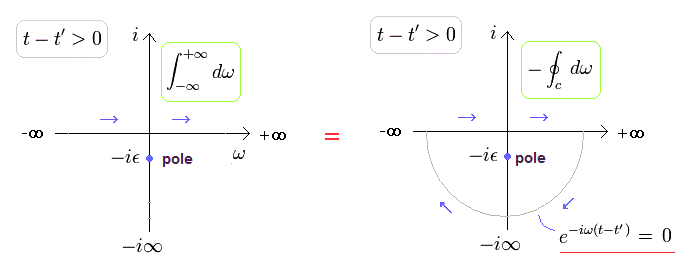
Fig.2 に示すように、"極" は マイナスの虚数部分にあるので、ゼロにならない。
Eq.4 を展開すると、係数 c-1 は 次のように " 1 " になる。
(Eq.9)

Fig.2 は 時計周りの閉曲線であるため、 計算結果は逆になる ( 1 → -1 ).
(Eq.10)
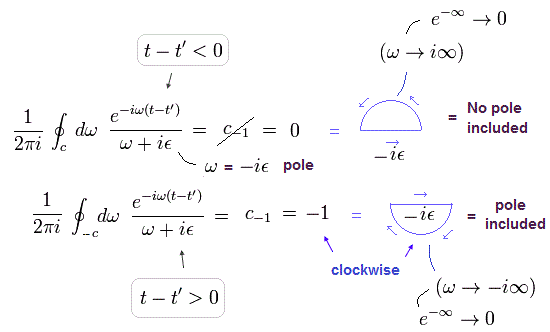
結果的に t-t' > 0 のとき、 階段関数 θ は "1" になる。
(Eq.11)
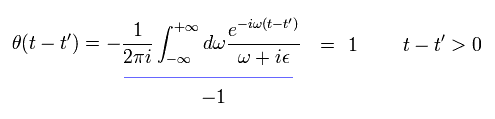
t-t' が 負 のとき ( t-t' < 0 )、Eq.4 の指数関数部分は ω → i∞ のときに ゼロになる。
(Eq.12)

つまり、Eq.4 の積分は 複素数場の 反時計回りの閉曲線と同等になる。
(Fig.3)
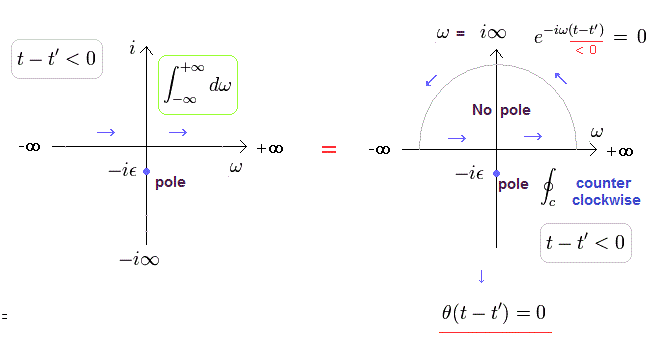
Fig.3 に示すように、この閉曲線は 極を含まない。
つまり t-t' が 負のとき、 θ は ゼロになる。
次に Eq.5 の階段関数について考える。
(Eq.5)
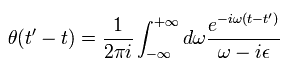
(Fig.4) Eq.5 の階段関数。
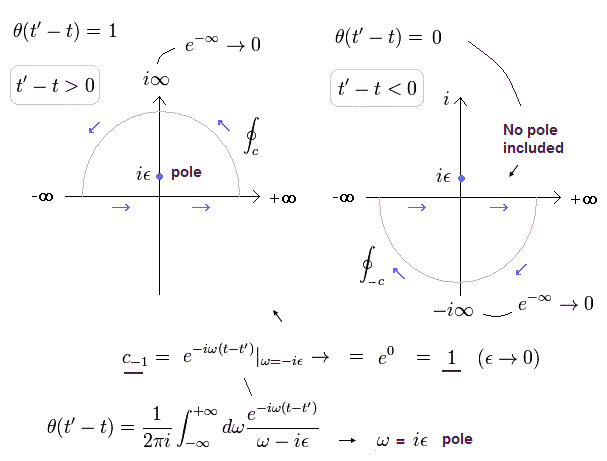
Eq.5 では、 "極" は Fig.4 に示すように プラスの虚数部分に存在する。
Eq.4 と同様な方法で、次の結果を得る。
(Eq.13)
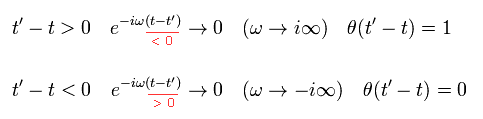
---------------------------------------------
(Eq.1) クライン・ゴルドンの波動関数。

Eq.1 の生成・消滅演算子は 次の交換関係を満足する。
(Eq.14)

Eq.1 の 2つの異なった波動関数を使って、次を計算する。
(Eq.15)
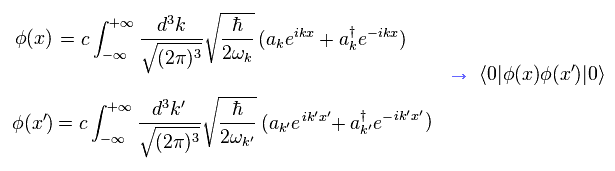
両サイドの真空と 消滅演算子の関係により、 aa† の項のみ残る。
(Eq.16)
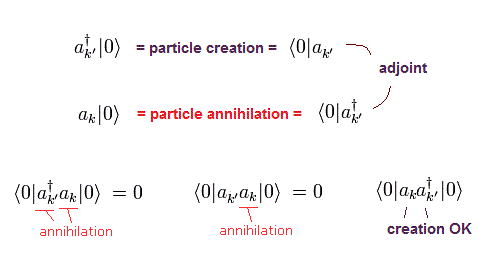
Eq.14 の交換関係を用いると、Eq.15 の結果は、
(Eq.17)

同様に、Eq.17 の x と x' を交換して、
(Eq.18)
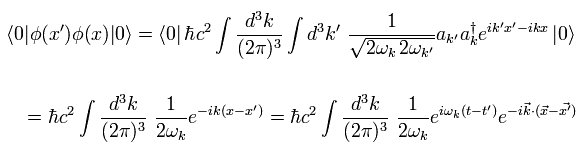
Eq.18 では、ωk は ki の偶関数である。
(Eq.19)
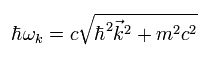
つまり、 ki の値が決まると、 ωk も 正の値に決まる。
Eq.18 において、 ki の 1-3 成分を変化させると ( k → -k )、指数関数 ( eikx ) 部分は Eq.17 のと同じになる。
(Eq.20)
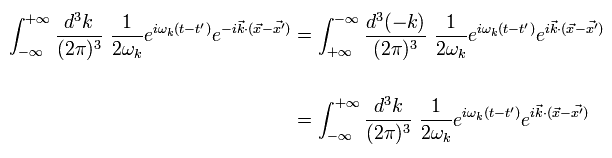
Eq.4 と Eq.17 を使用すると、 Eq.2 の最初の項は、
(Eq.21)

Eq.5 と Eq.18 (Eq.20) から、Eq.2 の 2番目の項は、
(Eq.22)

ω を k0 に変える。
(Eq.23)

結果的に Eq.2 の クライン・ゴルドンの伝播関数 は Eq.21 と Eq.22 の足したものになる。
(Eq.24)
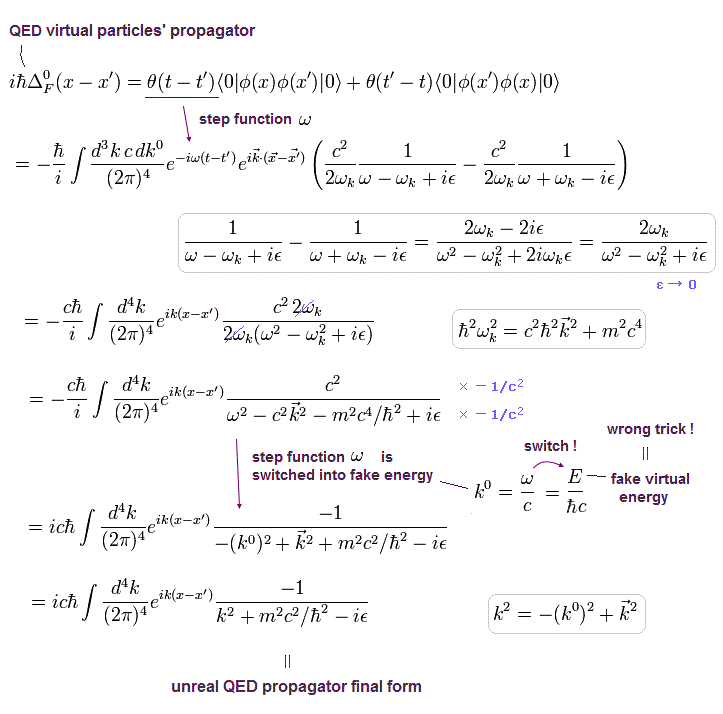
これを スカラー場の "伝播関数" (= グリーン関数 ) という。
スカラー場の伝播関数は 他の場の 基礎になるため、非常に重要である。
QED では、ディラックの伝播関数が主に使用されている。よって次に ディラック場について説明する。
このページに示したように、ディラック方程式の解は、
(Eq.25)
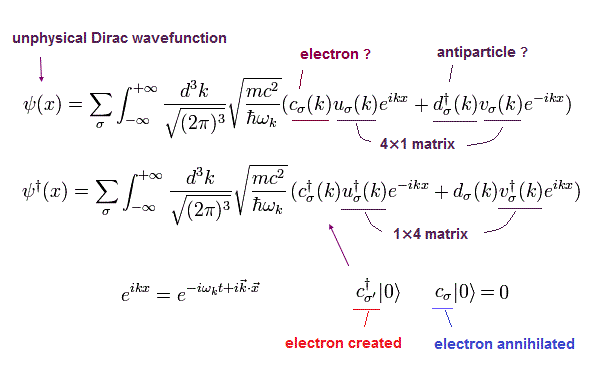
この共役な転置行列 (× γ0) は、
(Eq.26)
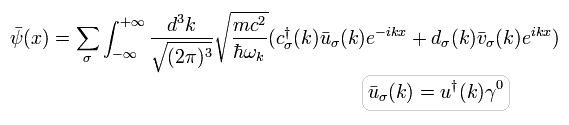
また 粒子 ( c, c† ) と 反粒子 ( d, d† ) は 次の 反交換関係を満たす。
(Eq.27)

他の組み合わせは 右辺でゼロになる。
ディラックの伝播関数は 次のように表される。
(Eq.28)

ディラック場は 反交換関係を満たす。 そのため "マイナス"の符号が Eq.28 の 第2項目に付加される。
両サイドの真空による消滅を考慮すれば、"cc†" の項のみ残る。
(Eq.29)
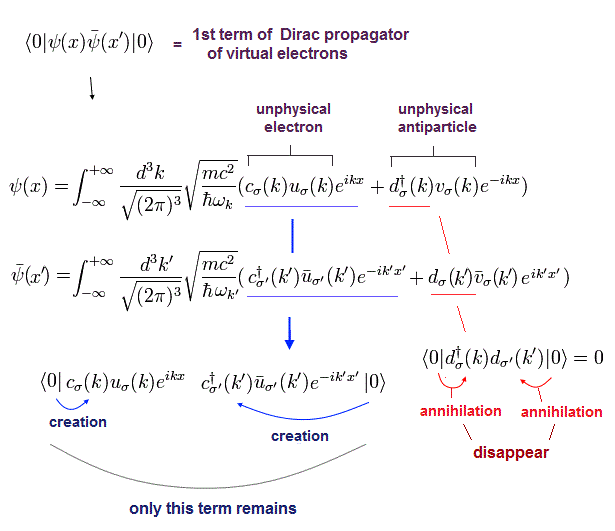
Eq.29 から、次を得る。
(Eq.30)
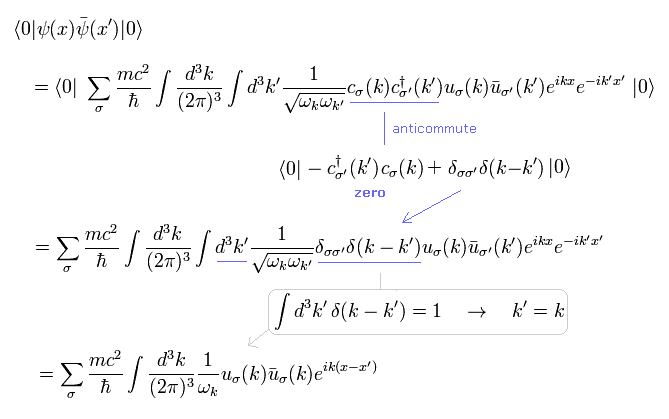
ここでは Eq.27 の反交換を使用した。
重要な点は Eq.30 の行列は 次のように 数にはなれないということである。
(Eq.31)
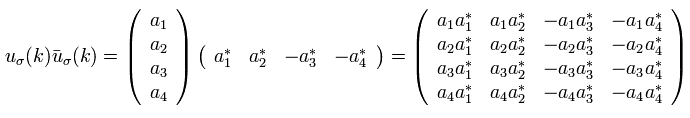
簡単に言うと、2つの行列 u は Eq.31 において ただ並んでいるだけである。
Eq.31 の状態は 次のように表せる。
(Eq.32)
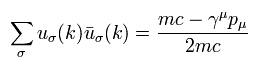
もし Eq.32 の2つの行列が結合せず ただ並んでいるだけとしたら、Eq.32 の右サイドから 別の u(k) をかけると、
(Eq.33)
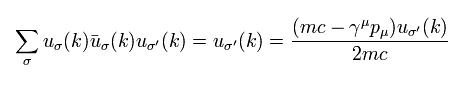
ここで 次の関係式を使用している。
(Eq.34)
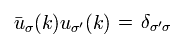
"u" の関係式に関しては、 このページを参照のこと。
Eq.33 は ちょうど次に等しい。
(Eq.35)
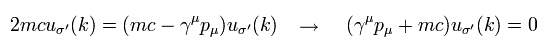
Eq.35 は このページの Eq.5-12 の u(k) の満たす関係式と同じである。
よって Eq.32 が正しいことが示された。
同様に、次を定義する。
(Eq.36)
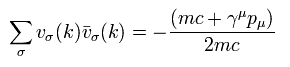
Eq.36 の右サイドから 別の v(k) を 付け加えると、
(Eq.37)
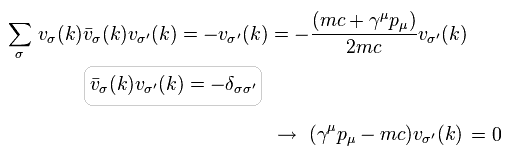
Eq.37 は このページの Eq.5-13 に等しい。
Eq.32 を用いると、 Eq.30 は、
(Eq.38)
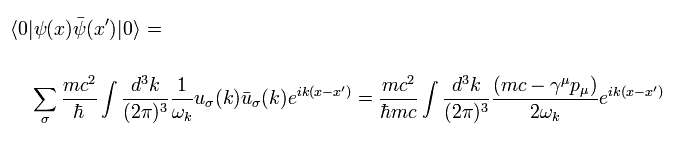
ディラックの伝播関数 (Eq.28) の 2項目を計算するとき、" c† c " の項は 消滅する。
(Eq.39)

ここでは " d d† " の項のみ残る。
(Eq.40)
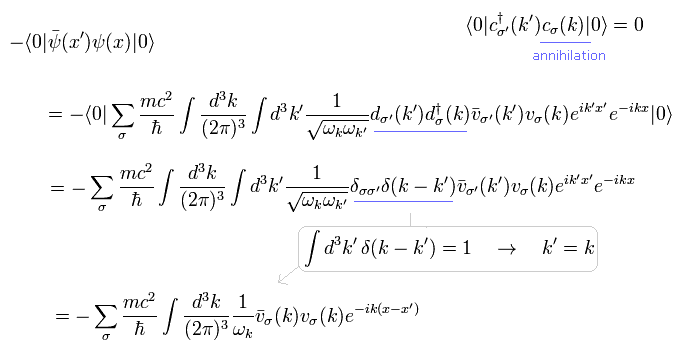
お気づきのとおり、 Eq.40 の 2つの行列 v(k) は 横行列 × 縦行列 である。
そのため Eq.40 は Eq.30 とは 完全に異なる。
ディラックの伝播関数を使うには、それらを同じものに "人為的"にそろえる必要がある。
Eq.36 を使うと、Eq.40 は
(Eq.41)

Eq.41 の 係数 pμ は ディラックの微分演算子に 由来している。
そのため 最終形で 指数関数部分を変更すると、それらは変化する。
(Eq.42)
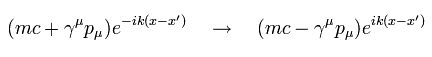
そのため 基本的に ディラックの伝播関数は 係数を除けば Eq.24 の クライン・ゴルドン場の伝播関数に似ている
(Eq.43) クライン・ゴルドンの伝播関数。
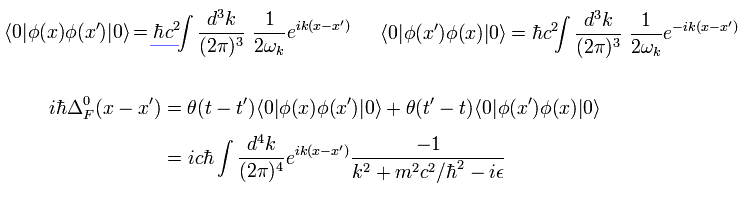
(Eq.44) ディラックの伝播関数。
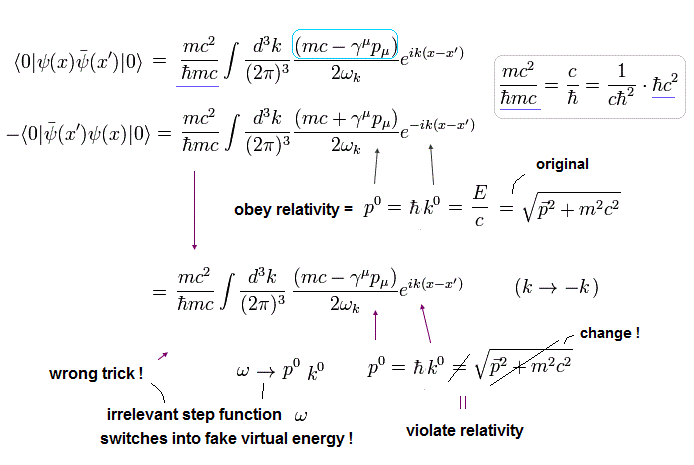
Eq.43 と Eq.44 を比較すると、ディラックの伝播関数は
(Eq.45)

Eq.45 は ディラックの伝播関数で QED では 頻繁に使用される。
このページに示したように、真空中の 電磁場のラグランジアンは 次のように表される。
(Eq.46)
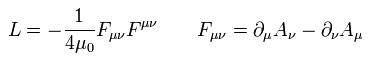
Eq.46 に示したように、 もし μ と ν が同じならば、 Fμν は ゼロになる。
つまり、正準な運動量のゼロ成分は 次のようにゼロになる。
(Eq.47)
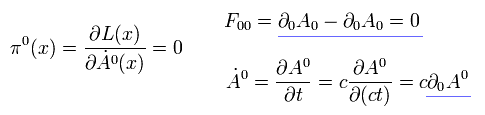
しかし 後で説明するように、もし ゼロ成分の光子を定義できないと、伝播関数の計算は不可能になる。
そのため ゼロ成分の正準な運動量を "強制的"に作る必要がある。
ゼロ成分を含むラグランジアンを次のように定義する。
(Eq.48)
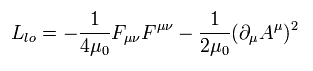
これを " ファインマンゲージのラグランジアン " という。
( ここでは 通常の SI 単位系を使用しているため、透磁率 μ0 が付加されている。 )
Eq.48 の2項目は 次のローレンツ条件を考慮すると消失する。
(Eq.49)
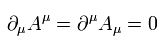
そのため ゼロ成分の正準な運動量は ( x0 = ct )、
(Eq.50)
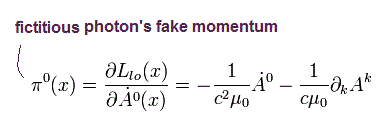
ここで 関係しているラグランジアンは、
(Eq.51)
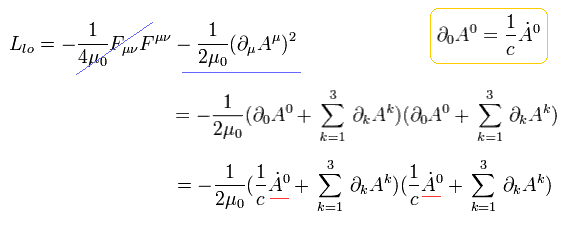
また 他成分 ( j = 1, 2, 3 ) の正準な運動量は
(Eq.52)
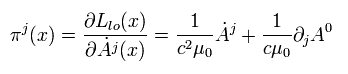
ここで 関係しているラグランジアンは、
(Eq.53)
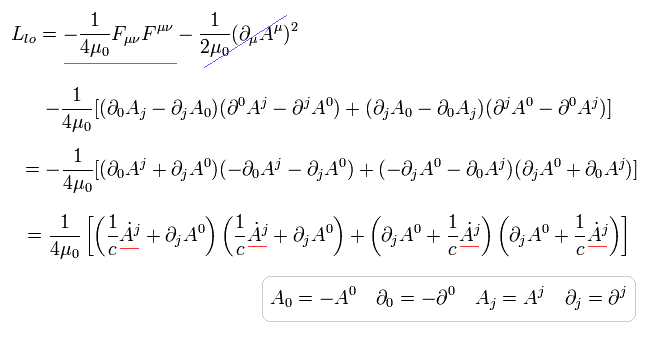
Eq.48 の μ と ν は 0 - 3 成分すべてを含んでいる。
そのため 係数 1/4 (と 1/2) がキャンセルされる。
ドブロイの関係式のように、交換関係を定義できる。
(Eq.54)
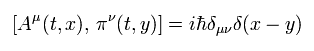
すると、
(Eq.55)
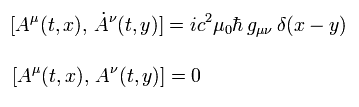
ここで gμν が現れる。
他の組み合わせは すべてゼロになる。
Eq.55 を用いると、Eq.54 を 次のように 証明することができる。
(Eq.56)
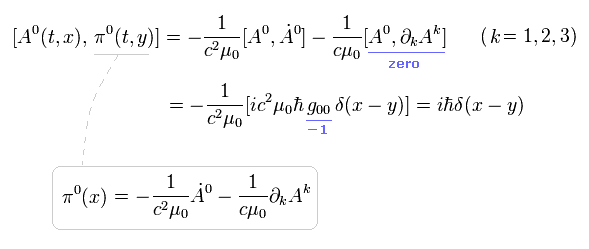
と
(Eq.57)
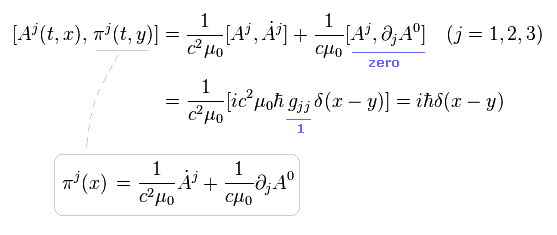
ここでは (-1,1,1,1) バージョンの計量テンソル g を使用している。
このページも参照のこと。
このページに示したように、 マクスウェル方程式を満たす解 Aμ (x), は、
(Eq.58)
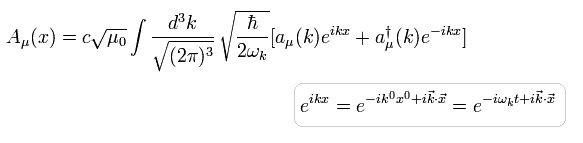
Eq.58 の時間微分は
(Eq.59)
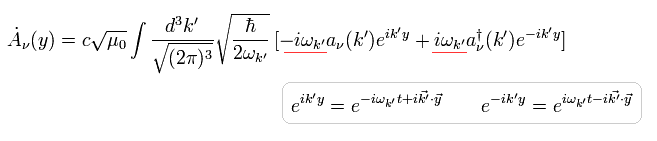
Eq.55 を満足するためには、次の関係式が有効でなければならない。
(Eq.60)
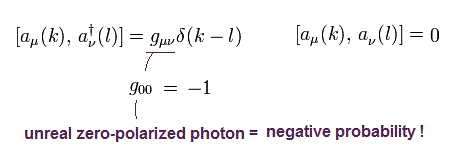
他のすべての組み合わせはゼロになる。
Eq.60 に示すように、光子の ゼロ成分のみ "負"のエネルギー ( = "負" の数 ). ( g00 = -1 ) を持つ。
つまり このゼロ成分の光子は 実在のものではない。
もちろん、Eq.49 のローレンツゲージ条件を考慮すると、このゼロ成分の光子は除去できる。
この奇妙な性質は Eq.48 の2項目の負の符号に起因する。
( この負の符号は人為的に付けられた。)
では どうして Eq.48 もしくは Eq.60 で 負の符号を定義してのか?
じつは Eq.60 に負の符号を定義しないと、g因子の計算ができないのである。
言いかえれば g因子を計算するために 奇妙な Eq.60 の関係式が導入されたのである。
このことを後で説明する。
次に Eq.60 の関係式を使用して Eq.55 を証明する。
Eq.58 と Eq.59 を Eq.55 に代入すると、
(Eq.61)
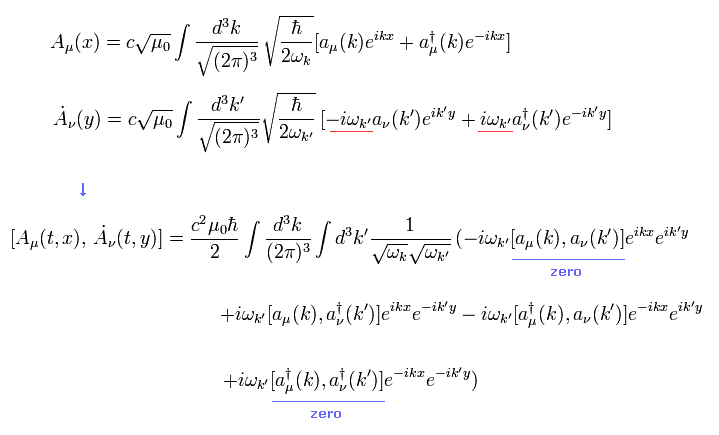
ここで
(Eq.62)
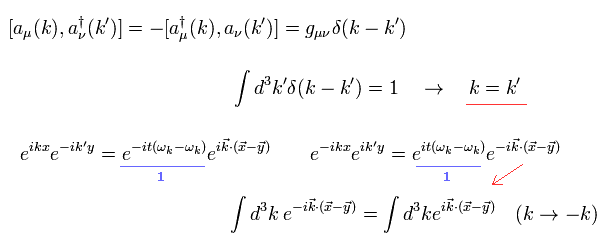
時間 t は同時刻である。
Eq.61 と Eq.62 から 次を得る。
(Eq.63)
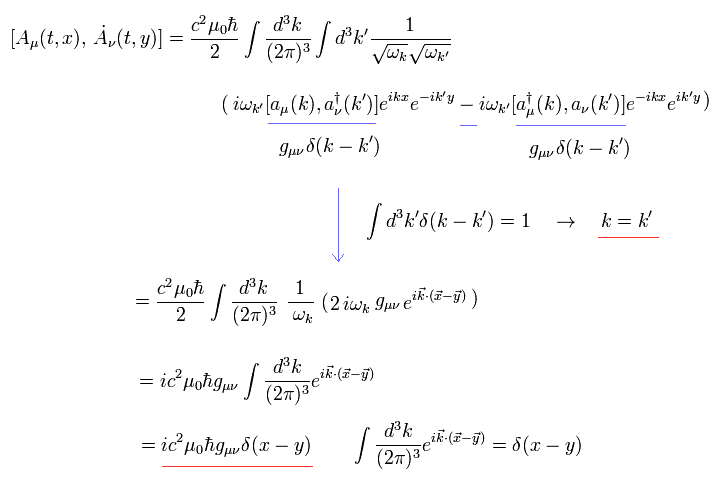
Eq.55 が得られた。
Eq.58 は Eq.1 に似ている。
つまり、光子の伝播関数は ゼロの質量を除いて Eq.24 の クライン・ゴルドン場のと ほぼ同じである。
よって 光子の伝播関数は
(Eq.64)

ゼロ成分の光子のみ、符号が 逆になる。
また 光子は ベクトルのため、違う成分の光子間の伝播関数は Eq.64 に示すように ゼロになる。
ここでクーロンゲージのハミルトニアンについて簡潔に説明する。
スカラーポテンシャル (= A0 ) が ゼロのとき、
(Eq.65)
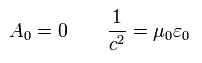
ハミルトニアンは、
(Eq.66)
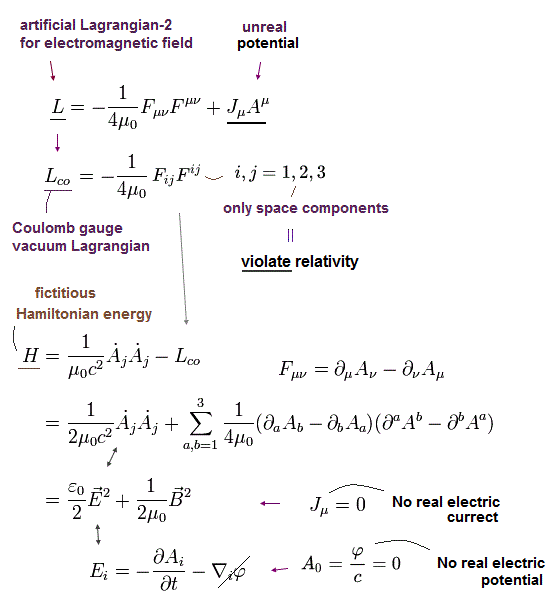
このサイトでは ローレンツゲージを用いるため これに "マイナス"エネルギーのゼロ成分の光子を付け加える必要がある。

2013/1/25 updated This site is link free.