トップページ (ヘリウムも含む正確な新ボーア模型)
超対称性粒子は 時間の無駄。
(Eq.1)
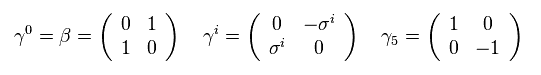
このページでは、 このサイトの表記法を利用する。
Eq.1 は γ 行列のカイラル表現である。
このページのみ ( 1, -1, -1, -1 ) バージョンの計量テンソルを利用する。
また σ は 次のようなパウリ行列である。
(Eq.2)
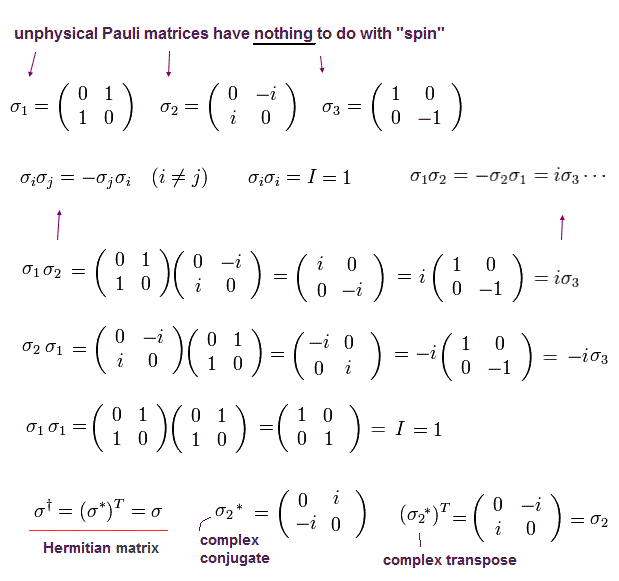
Eq.1 から、次を得る。
(Eq.3)
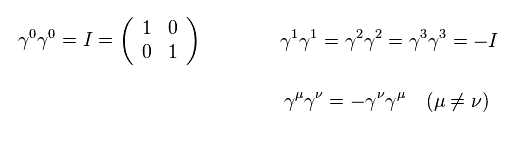
ここでは 4 × 1 のディラックスピノル Ψ を採用する。
(Eq.4)
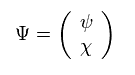
ディラック方程式は、
(Eq.5)
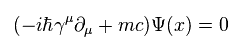
ここでは
(Eq.6)
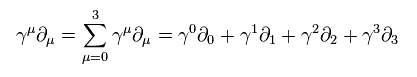
ここでは 自然単位を利用する。
(Eq.7)
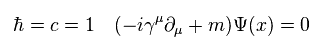
Eq.7 に γ0 を左側から かけて、
(Eq.8)
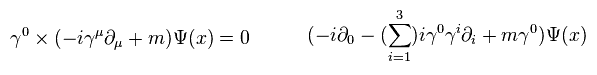
ここでは
(Eq.9)
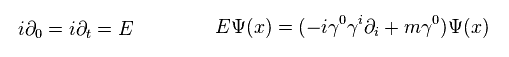
"E" は エネルギーで、時間微分を表す。
運動量演算子 (= p ) は、
(Eq.10)
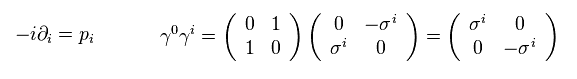
Eq.10 と Eq.4 を用いると、 Eq.9 は、
(Eq.11)
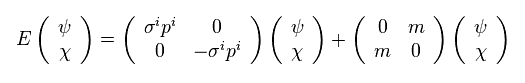
Eq.11 から、2つの式を得る。
(Eq.12)
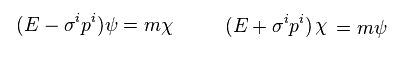
ここでは
(Eq.13)
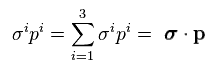
フェルミ粒子の質量がゼロ ( m = 0 ) のとき、Eq.12 は、
(Eq.14)
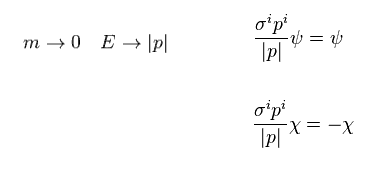
Eq.14 を見て分かるように、上 2 成分のスピノル ψ は 正 のヘリシティーを持つ (= σp )。
これはつまり スピン (= σ ) と 運動量 (= p ) の方向が 同じ (= 右巻き ) であることを意味する。
一方で、下 2成分のスピノル (= χ ) は 負のヘリシティーを持つ。
つまり 左巻きのスピノルということになる。
(Eq.15)
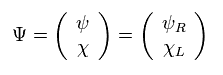
スピノルに γ5 行列を用いると、上下のスピノルは 異なった符号を与える。.
(Eq.16)
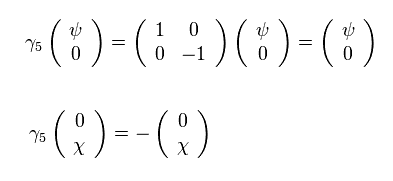
ディラック方程式をローレンツ変換で不変にするには スピノルのローレンツ変換を
定義する必要がある。
ここで 彼らは 次の S 演算子を導入した。
(Eq.17)
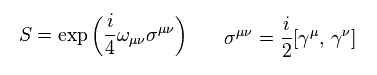
Eq.17 では、 ω は 反対称の定数である。
また σμν は 2つの γ 行列の交換子である。
( この σ は パウリ行列ではない。 )
(Eq.18)
すると、
(Eq.19)
Eq.18 と Eq.19 を用いて、 Eq.17 の無限小ローレンツ変換は、
(Eq.20)
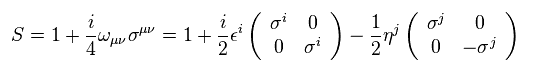
Eq.20 では、 ω を 異なった定数 ε と η で表している。
Eq.20 のローレンツ変換演算子を Eq.15 のディラックスピノルに作用させると、
(Eq.21)
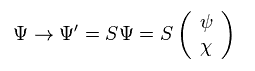
Eq.20 と Eq.21 から 次を得る。
(Eq.22)
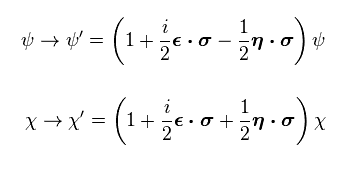
Eq.20 から、 Eq.20 の逆行列は、
(Eq.23)
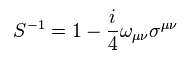
なぜなら、
(Eq.24)
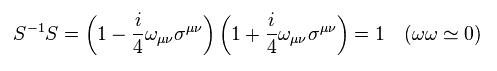
Eq.1 と Eq.2 から 次を得る。
(Eq.25)

Eq.17、 Eq.20、 Eq.23、 Eq.25 から 次の関係式を得る。
(Eq.26)
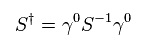
ここでは次を使っている。
(Eq.27)
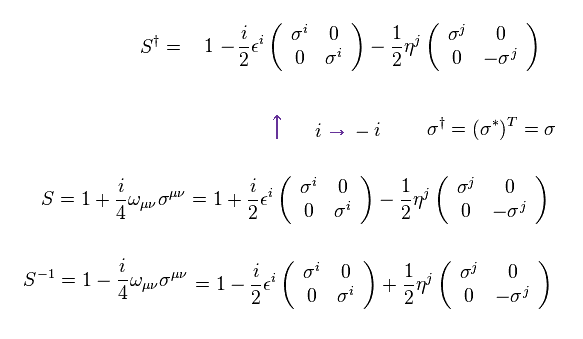
結果、
(Eq.28)
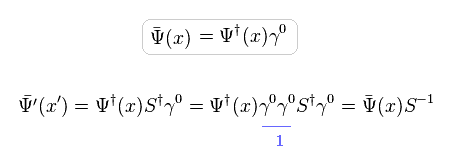
よって、ディラックラグランジアンは ローレンツ変換 (= S ) の下で 不変になる。 ,
(Eq.29)
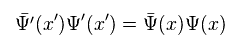
Eq.27 のように 次を定義する。
(Eq.30)
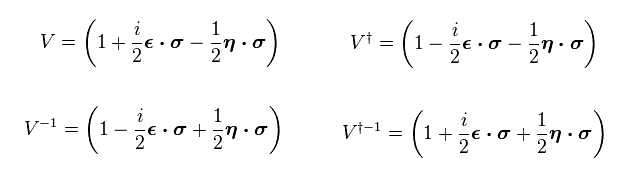
Eq.30 では、パウリ行列 σ はエルミト行列である。
そのため σ の 共役な転置行列は 同じままである ( σ† = σ )。
Eq.22 と Eq.30 から、次を得る。
(Eq.31)
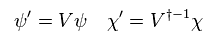
Eq.29 のラグランジアンは 次のように表せる。
(Eq.32)
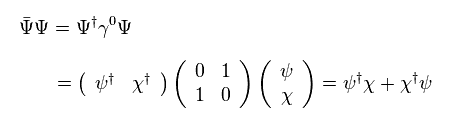
と
(Eq.33)
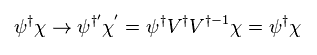
そのため Eq.32 が スカラーラグランジアンであることを証明できた。
ここでは 次の表記法を 使用する。
(Eq.34)
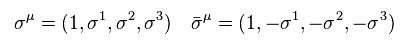
Eq.30 と Eq.31 から、次を得る。
(Eq.35)
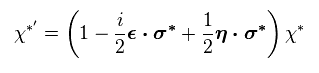
Eq.2 から、各パウリ行列は 次を満たす。
(Eq.36)
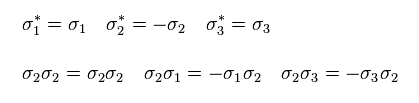
なぜなら σ2 のみが 虚数だからである。
Eq.35 と Eq.36 から、次を得る。
(Eq.37)
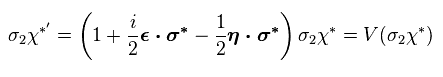
Eq.37 は この波動関数は Eq.31 の ψ のように変換することを表している。
(Eq.38)
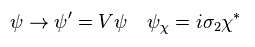
Eq.33 のように、
(Eq.39)
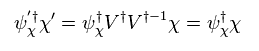
Eq.38 を用いると、 Eq.39 は、
(Eq.40)
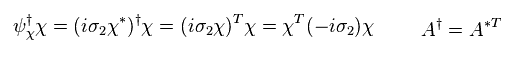
Eq.40 では、 i* = -i と、 σ2* =- σ2 を使った。
また、
(Eq.41)
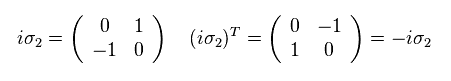
Eq.41 より、
(Eq.42)
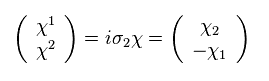
ここで 次を定義する。
(Eq.43)
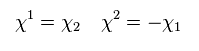
Eq.42 と Eq.43 から、
(Eq.44)
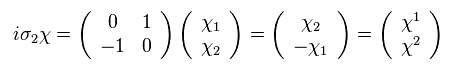
(Eq.45)
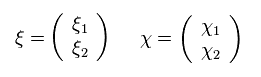
Eq.44 と Eq.45 から、
(Eq.46)
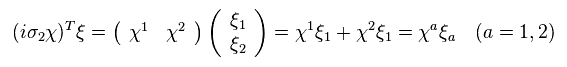
Eq.44 を使うと、 Eq.46 は、
(Eq.47)
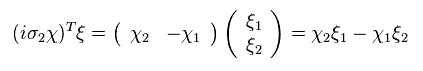
E.47 は ローレンツ不変な スカラーである。
χ と ξ は フェルミ粒子なため、 Eq.47 の反交換子は ゼロにならない。
ここで 新たな演算子 εab を導入する。
Eq.43 と Eq.44 から、次を得る。
(Eq.48)
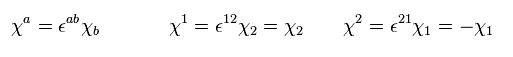
つまり、
(Eq.49)
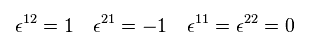
Eq.48 は 次に等しい。
(Eq.50)
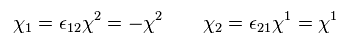
よって、
(Eq.51)
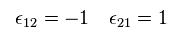
Eq.49 を用いると、次のように表せる。
(Eq.52)
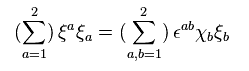
外電磁場の下で、ディラック方程式は ベクトル ( スカラー ) ポテンシャル A を含む。
(Eq.53)
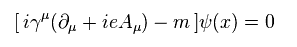
Eq.53 の 複素共役は、
(Eq.54)
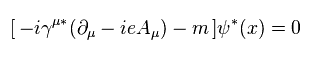
Eq.1 と Eq.3 より、次の関係式を得る。
(Eq.55)
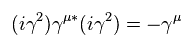
なぜなら
(Eq.56)
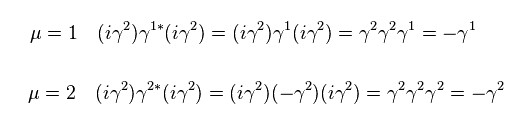
Eq.54 に 左側から ( iγ2 ) を掛けると、
(Eq.57)
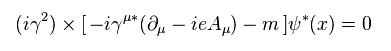
Eq.57 の最初の項は 次のように表せる。
(Eq.58)
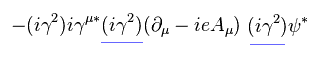
ここで 次を挿入する。
(Eq.59)
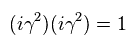
Eq.55 と Eq.58 を用いると、 Eq.57 は、
(Eq.60)
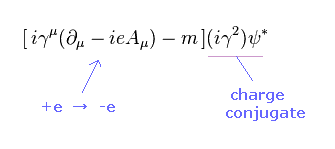
Eq.53 と Eq.60 を比較すると、Eq.60 の電荷 "e" は Eq.53 と逆になることが分かる。
(= ψ の 荷電共役 は iγ2ψ*. になる 単なる人為的なルールにすぎないが。 )
次を定義すると、
(Eq.61)
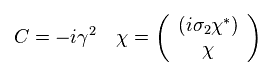
次を得る。
(Eq.62)
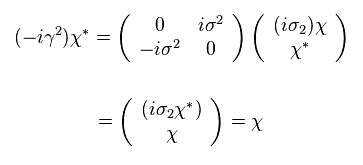
これはつまり スピノルが Eq.61 の形をしているとき、波動関数の荷電共役は 元の状態と 同じになる。
荷電共役は 反粒子のため、このケースでは 粒子と反粒子が 同じになる。
(Eq.63) マヨラナ粒子?
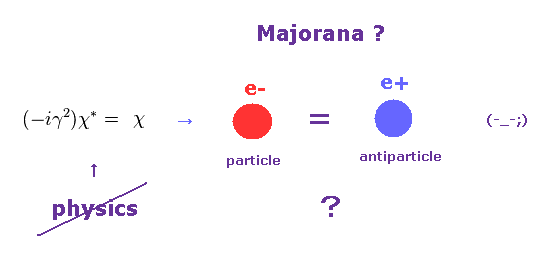
彼らは この状態を マヨラナ粒子と呼んだ。
ニュートリノ、フォティーノなどは マヨラナフェルミ粒子と言われている。
しかし たったこれだけの 抽象的な 数式演算子のみでは、まったく物理的な説明をしたことにならない。
(Eq.64) 超対称性ラグランジアン ?
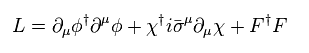
Eq.64 は 最も簡単な 超対称性ラグランジアンの 1例である (= Wess-Zumino モデル )。
φ は ボソン、 χ は フェルミ粒子 ( ここでは 簡単な マヨラナフェルミ粒子を考える。 ).
そして "F" は "非実在的"な 補助場 (= ボソン ) で、これは 超対称性の代数関係を満たすのに必須なものである。
もちろん、これらの補助場というのは 人為的な概念以外何者でもなく、 超対称性理論自体は 物理というより、単なる 数式記号であることを 端的に示している。
(Eq.12)
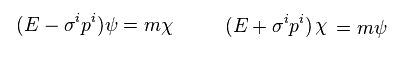
Eq.12 の 右側のディラック方程式より、次を得る。
(Eq.65)
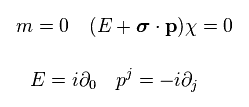
これは、
(Eq.66)
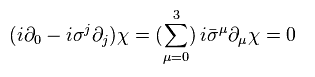
ここで 次を用いている。
(Eq.34)
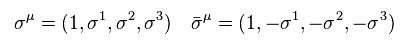
このサイト (p.33) に示したように、 全ラグランジアン (= L )、ボソン (= φ )、フェルミ粒子 (= χ )、 F ボソンの単位は 次のようになる。
(Eq.67)
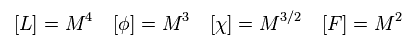
ここで 次の自然単位系を用いている。
(Eq.68)
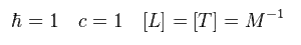
彼らは ボソン φ の 超対称性変換 を次のように定義した。
(Eq.69)
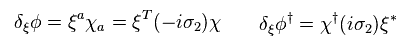
もちろん、ボソンは フェルミ粒子と異なる。
つまり、1つのボソン (= φ ) を表すのに 2つのフェルミ粒子 (= ξ, χ ) が 必要になる。
Eq.67 と Eq.69 から、 この 奇妙なフェルミ粒子の ξ の単位は、
(Eq.70)
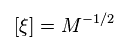
つまり この ξ は Eq.67 の 元のフェルミ粒子 χ と根本的に異なるものである。
これら 非実在のフェルミ粒子やボソンに頼るということは、超対称性自体 真実ではないことの証である。
(Eq.71)
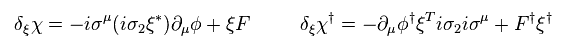
そして フェルミ粒子 χ (= Eq.71 ) や ボソン F (= Eq.72 ) の超対称性変換を定義した。
もちろん、これらの形式は 人為的に導入されたもので 自然な現象を まったく表していない。
(Eq.72)
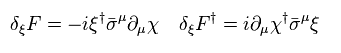
ラグランジアンのボソン部分 (= Eq.64 の最初の項 ) の超対称性変換は、
(Eq.73)
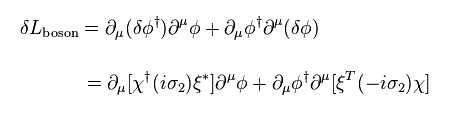
Eq.73 では、 Eq.69 が 挿入されている。
Eq.64 と Eq.71 から、フェルミ粒子の変換は、
(Eq.74)
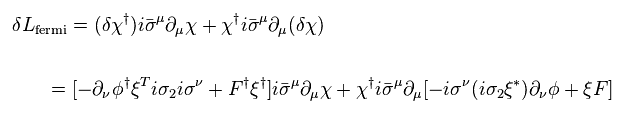
ここで パウリ行列の反対称的性質を用いる。
また 部分積分では 全体に マイナスの符号がつく。
(Eq.75)
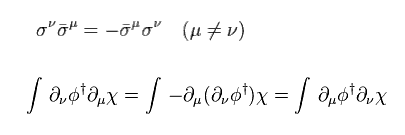
Eq.36 を用いて、
(Eq.76)
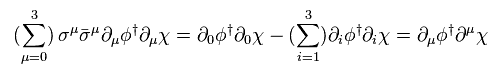
結果的に、 Eq.74 は、
(Eq.77)
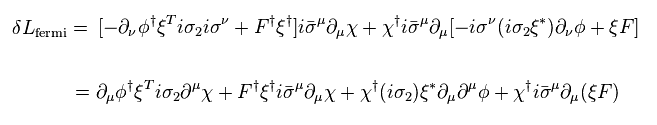
再び、部分積分で 全体に マイナスの符号がつく。
(Eq.78)
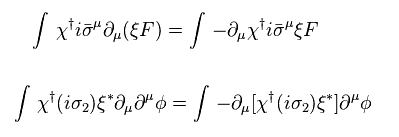
Eq.72 を用いると、補助場 FF は 次のように変換する。
(Eq.79)
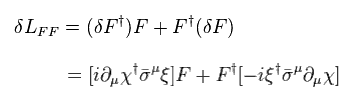
Eq.73、 Eq.77、 Eq.79 から、全ラグランジアンの変化は ゼロ になる。
(Eq.80)
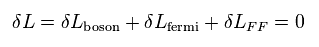
Eq.80 は Eq.64 のラグランジアンは Eq.69, Eq.71, Eq.72 の 超対称性変換の下で 不変であることを意味している。
これを "超対称性" という。
見てのとおり、物理学者達は ラグランジアンと超対称性変換で不変にするために 数々の 人為的な定義を導入しようとしている。
この手法をみれば、超対称性自体が 自然界の法則を 表わす ”自然な”理論とは 到底言えないことが すぐに理解される。
基本的に、 MSSM (= minimal supersymmetric standard model、最小超対称標準模型 ) のラグランジアンは、
(Eq.81)
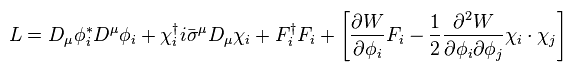
Eq.81 の最後の項は ポテンシャルエネルギーである。
また "D" は 共変微分である。
(Eq.82)
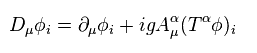
Eq.82 では、 A は ベクトルポテンシャルで、ゲージボソンである。
超対称性とローレンツ不変の 厳しい制限の下で、 W の形式は 次に限定される。
(Eq.83)
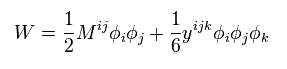
さらに ベクトルポテンシャル ( ex. 光子 ) のラグランジアンを追加できる。
(Eq.84)
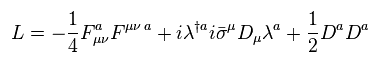
Eq.84 の λ は "フォティーノ" であるが、物理的実態がなく、単なる数式記号にすぎない。
Eq.84 の反対称テンソルは、
(Eq.85)
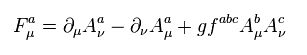
ヒッグス (= H ) と 他の粒子間の相互作用ハミルトニアンは、
(Eq.86)
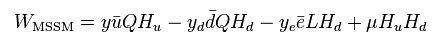
Eq.86 は ヒッグス粒子自体も含めた粒子に "質量" を与える。
超対称性は 破れてなければならず、超対称性粒子の ラグランジアンの 質量項は、
(Eq.87)
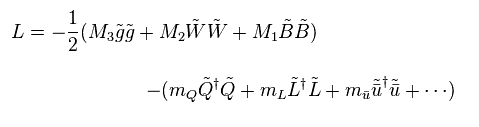
この 破れ ( SUSY breaking ) のために、 124 もの 自由に設定できるパラメーターが MSSM に出現することになる。
つまり、超対称性理論は 何も予測することができない無用の長物と言える。
MSSM は R パリティーなるものを定義している。
もちろん、この R パリティーというのは 単なる人工的なルールにすぎず、自然な帰結でも何でもない。
(Eq.88)
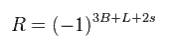
通常の粒子は 必ず R = +1 を持ち、 超対称性粒子は R = -1 を持つ。
例えば、通常のクォークでは、 B (= バリオン数 ) は 1/3、 L (= レプトン数 ) は ゼロ、
スピン S は 1/2 である。
(Eq.89)
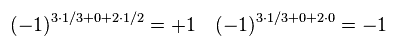
Eq.89 の左が 通常のクォークの R パリティーで、右が squark のものである。
squark の スピン S は ゼロのため、 R パリティーは -1 になる。
現在の 役に立たない場の量子論は、 ある変換のもとでの ラグランジアン L ( もしくは 作用 S ) の不変性を もっとも重要な概念と考えている。
作用 S の変分は 次のように表せる。
(Eq.90)
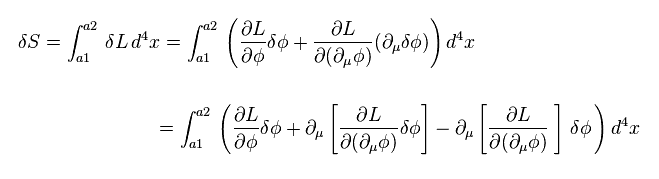
ここで 次のオイラー・ラグランジュ方程式を使う。
(Eq.91)
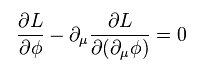
Eq.90 は、
(Eq.92)
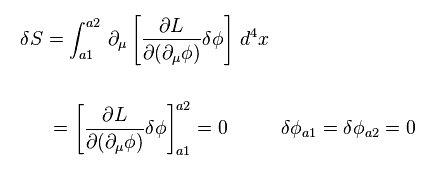
Eq.90 に示したように、"全微分"の積分はゼロになる。
これはつまり、オイラー・ラグランジュ方程式が成り立つとき、作用 S は 任意の変換の下で
不変になる。
ここで 次のように 人工的な電流 J を定義すると、
(Eq.93)
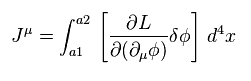
Eq.92 は 次のように表せる。
(Eq.94)
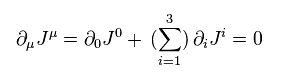
Eq.94 は、 人工的な 電荷 Q を 次のように定義すると、
(Eq.95)
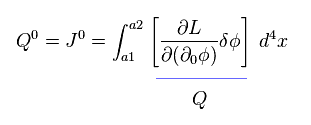
この全電荷は 保存される。
超対称性理論家は この 非実在の電荷 Q を最も重要な概念と考えている。
まったくもって 奇妙である。
一般的に 任意の変換は この電荷 Q を用いて 次のように表される。
(Eq.96)
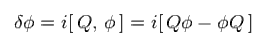
ここで 次のラグランジアンを用いる。
(Eq.64)
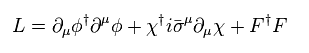
ボソン場 φ の 正準運動量 π は、
(Eq.97)
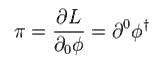
ここで、この φ と その 正準運動量 (= π ) の交換関係を定義する。
(Eq.98)
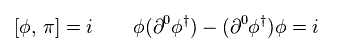
Eq.95 と Eq.64 から、電荷 Q は 次のようになる。
(Eq.99)
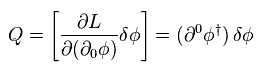
Eq.98 と Eq.99 を用いて、次を得る。
(Eq.100)
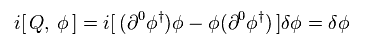
Eq.96 を証明できた。
(Eq.101)
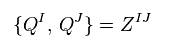
変換 (= Q ) の種類が複数あるとき、これら Q の反交換子は Eq.101 の
セントラルチャージ Z というものを与える。
この 抽象的な セントラルチャージをキャンセルするために、超弦理論は 非現実的な 10 次元 を必要とする。 このページを参照のこと。
見てのとおり、超対称性理論や 超弦理論では 物理的実態を伴わない 数式のみで 勝手に理論を定義していく手法に完全に依存している。
困ったものである。
基本的に 回転の演算子は 次のように表せる。
(Eq.102)
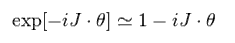
"J" は 角運動量で、 θ は角度である。
スピノル回転の場合では、 J は パウリ行列 (= σ/2 ) になる。
(Eq.103)
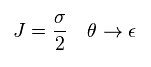
超対称性の電荷 "Q" は スピノルのため、次のように変化する。
(Eq.104)
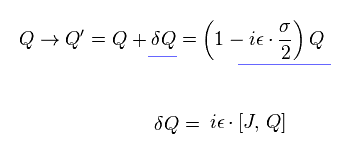
次を定義すると、
(Eq.105)
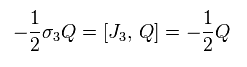
次を得る。
(Eq.106)
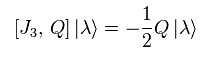
と
(Eq.107)
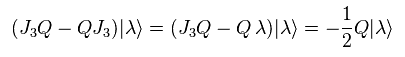
結果、
(Eq.108)
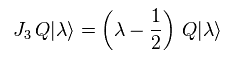
Eq.108 は 電荷 Q は 粒子のスピン 1/2 を 減らす作用があることを示している。
しかし、超対称性の理論家達は この電荷 Q (= スピンストッパー !? ) が いったい何者なのか 絶対に答えようとしない。
(Eq.109)
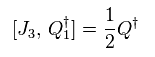
Q の複素共役の場合は、
(Eq.110)
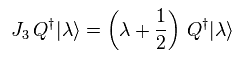
スピン 1/2 は 増加する。
(Eq.111)
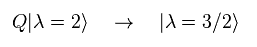
この電荷 Q を スピン "2" のグラビトンに作用させると、それは スピン 3/2 の グラビティーノに変化するらしい。
残念ながら、たったこれだけの抽象的な数式の定義のみでは スピンの実態に 答えたことにはまったくならない。
(Eq.112)
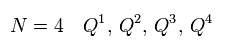
超対称性変換の種類が 4つあるとき、これを "N=4" の超対称性 と呼ぶ。
このケースでは、異なった Q の数は "4" である。

2014/5/7 updated This site is link free.