
トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは実在しない。
何が実在の素粒子か?
このホームページでは このページに示したように 相対論的な四元ベクトルとして ( -1, +1, +1, +1 ) のバージョンを使用する。
また 次の関係式をこのホームページでは使用する。
(Ap. 1) このホームページ。

LI は ラグランジアンの相互作用項である ( q = 電荷, A = ベクトルもしくはスカラーポテンシャル, ψ = ディラックの波動関数 )。
また c(k) と c†(k) は 粒子の消滅生成因子を意味している。
u(k) と v(k) は ディラックのスピノルである ( このページも参照のこと)。
最後の行は 真空からの粒子の生成 (波数が k ) を表している。
他の本では Ap.1 の代わりに 次の表記を使用しているものもある。
(Ap. 2) 他の教科書。

薄い緑で囲った部分は Ap.1 と Ap.2 で異なっている部分である。
しかし、ディラックの波動関数の反交換 のところは 両者で同じになっている。(互いの違う部分をキャンセルしている。)
これらの関係式に基づいて 必要なところで 表記を変更するといい。
ラザフォード散乱は 1911 年に ボーア模型などを使って、ラザフォードによって提唱されたものである。
彼は 金原子核とα粒子(アルファ粒子)を 点粒子と考えて、α粒子が クーロン反発力によって散乱されると考えた。
2つの荷電粒子が近づくにつれて、それらの間の クーロン相互作用 (反発もしくは引力) は強くなる。
結果として α粒子は 90°以上の大きい角度でときどき散乱される。
もし 標的原子核が 点粒子でないとすると、散乱パターンは クーロン相互作用パターンと異なることになる。
結果は 金原子核は 点粒子のパターンをとった。
彼は 古典力学の方法を使った。
最初に その古典力学的手法で ラザフォードの散乱公式を導くことにする。
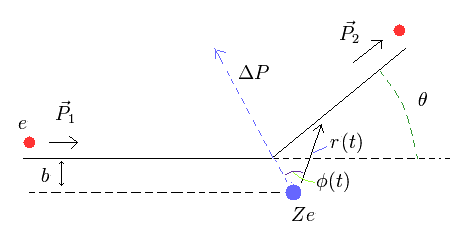
Fig.1 ラザフォード(クーロン)散乱モデル。
微分散乱断面積は 次のように 細いリング状のところの面積に等しい。
(Eq.1)
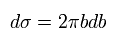
Eq.1 から、
(Eq.2)
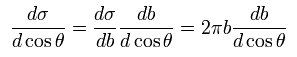
ここで 粒子の散乱前後の運動量の大きさは変化しないものとする。
つまり その方向のみ変化するとする(= 弾性散乱)。
(Eq.3)
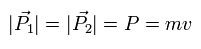
ここで m は 粒子の質量で v は速度である。
粒子の散乱前 (= P1 ) と散乱後 (= P2) の運動量の方向の間の角度が θ, のとき、運動量の変化は
(Eq.4)
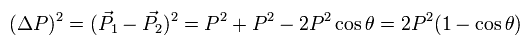
cosθ を 1 - 2 sin2 (θ/2) に変えて、
(Eq.5)
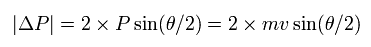
運動量の変化は 散乱の全過程で 粒子の受け取った 力積 (= Ft) に等しい。
(Eq.6)
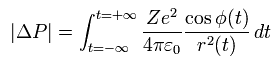
ここで 力は 2つの電荷 ( e と Ze ) の間に働くクーロン力、 φ(t) は その力積の方向と r(t) (= 位置ベクトル) の間の角度を意味している。
これらのクーロン相互作用のもとでは、角運動量 (L) が保存される。
Fig.1 に示すように、 最初の 角運動量は mv × b である。
(Eq.7)
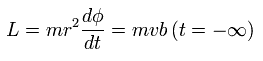
Eq.7 から、
(Eq.8)
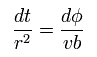
Eq.6 と Eq.8 から、
(Eq.9)
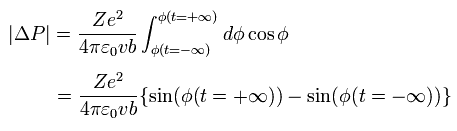
ここで、
(Eq.10)
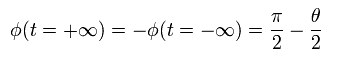
Eq.10 を Eq.9 に代入して、
(Eq.11)
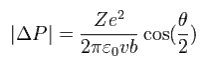
Eq.5 と Eq.11 より、
(Eq.12)
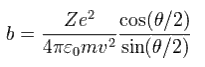
Eq.12 から、
(Eq.13)
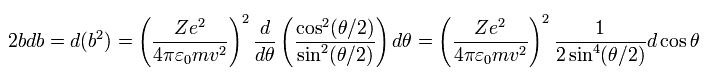
ここで 次の関係式を使う。
(Eq.14)
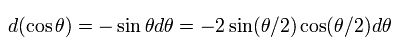
立体角 (Ω) を使うと、微分散乱断面積 ( ラザフォード散乱公式 ) は、
(Eq.15)
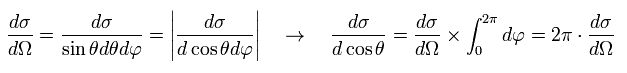
Eq.1、 Eq.13、Eq.15 より、
(Eq.16)
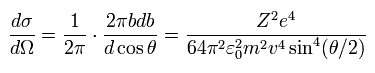
Eq.16 は 古典力学による 有名なラザフォードの散乱公式である。
次に、QED の方法で ラザフォードの散乱公式を導くことにする。
QED の ディラック方程式は 相対論的かつ スピンの効果を含んでいる。
相対論効果を考慮すると、それは Mott 散乱と呼ばれる。
残念ながら、QED から 現実の世界を思い浮かべることはできない。それは単に "数学的な"言語である。
( 読者はこの事実を心に留めておく必要がある。)
QED においても、古典力学のクーロン相互作用を使用する。そのため スカラーポテンシャル ( A0 = φ/c ) は、
(Eq.17)
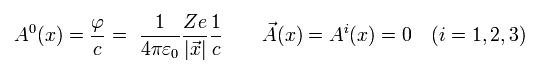
ここでは 静磁場を仮定しているので、ベクトルポテンシャル (= Ai ) はゼロになる。
Ap.1 と Eq.17 より、光子とフェルミ粒子間の ラグランジアンの相互作用項は、
(Eq.18)
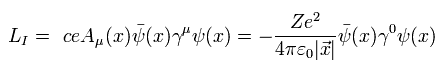
ここでは (-1, 1, 1, 1) のバージョンを使用している。
長い時間 T の間に 散乱される粒子 ( 電荷= e ) の数 (N) は、
(Eq.19)
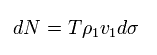
ここで ρ1 は 粒子の数密度、 v1 は その速度、 dσ は 微分散乱断面積である。
近似的に 速度 v1 は、
(Eq.20)
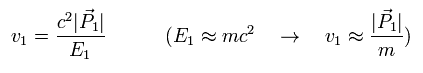
QED では、ある無限小の運動量空間 (= d3P2 ) に散乱される数は 次のように表される。
(Eq.21)
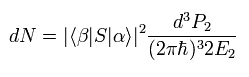
ここで α と β クーロン散乱の最初と最後の状態で、 S は S 行列 (S-matrix) である。
E と 2πħ は 規格化のために必要である。
S 行列は 次のように 相互作用ハミルトニアンの ユニタリー演算子として表される。
(Eq.22)
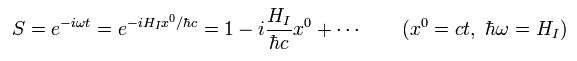
Ap.1 に示すように、 このホームページでは、波数 (k1) をもつ、最初の状態を次のように表す。
(Eq.23)
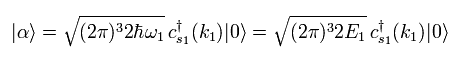
これらの係数は、Eq.21 の規格化因子によって 打ち消されることになる。
最後の状態は 次のように 消滅因子を使って表す。
(Eq.24)
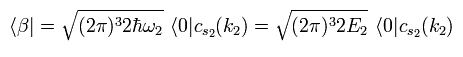
ここでは 最初と最後の状態は同じエネルギーを持つとしている。
そのため Eq.21 の規格化因子は 次のように表せる。
(Eq.25)
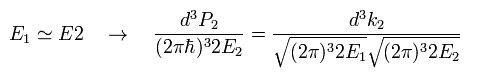
また この粒子の数密度 (= ρ1 ) を 次のように仮定する。
(Eq.26)
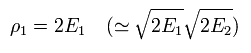
実は、この ρ1 の値は 人為的に 操作可能である。
この エネルギーの次元は 断面積の次元を 長さの二乗にするために導入される。
ローレンツ収縮を考慮すると、 密度と 相対論的なエネルギーの比は 次のように ローレンツ変換不変な形になる。
(Eq.27)
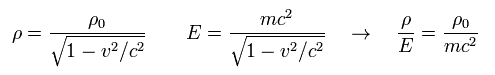
そのため、例えば Eq.26 の値を ローレンツ不変な形を維持して 次の形に変えることができる。
(Eq.28)
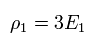
Eq.19, Eq.20, Eq.21, Eq.26 より、 微分断面積は、
(Eq.29)
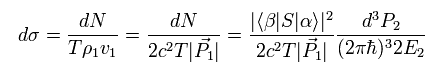
全エネルギーは保存されるので、遷移の確率振幅は次のように表せる。
(Eq.30)
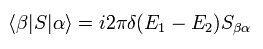
ディラックのデルタ関数は次のように表せる。
(Eq.31)
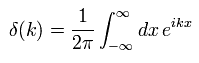
Eq.31 を使うと、 次の式が得られる。
(Eq.32)
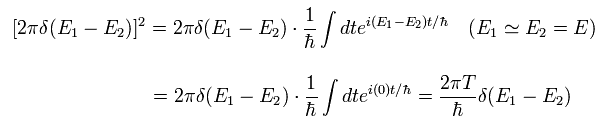
Eq.29 の微小運動量空間は 立体角を使って 次のように表せる。
(Eq.33)
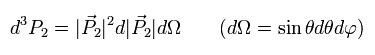
アインシュタインの相対論の公式によれば、
(Eq.34)
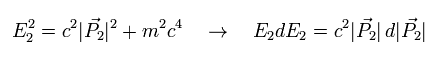
Eq.33 と Eq.34 から、
(Eq.35)
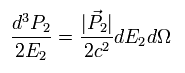
Eq.29, Eq.30, Eq.32, Eq.35 から、
(Eq.36)
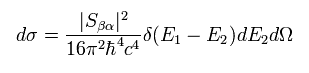
ここで |P1| = |P2| を使う。
Eq.36 を E2 で積分して、
(Eq.37)
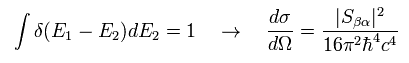
Eq.22 の S 行列においては、1次の相互作用のみ考慮する。
E.18 と Eq.22 から、
(Eq.38)
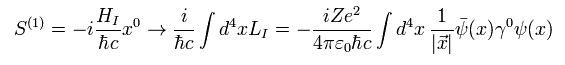
ここで LI は ラグランジアン密度を意味するので、 それを全空間 (+ 全時間 ) で積分している。
ここで 次の ディラックの波動関数を使用する。
(Eq.39)
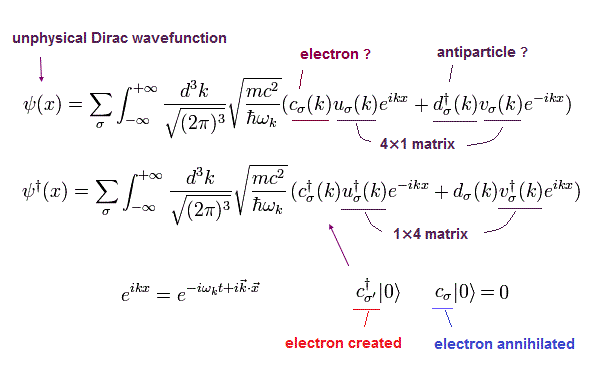
また、その共役な転置行列 (× γ0) は、
(Eq.40)
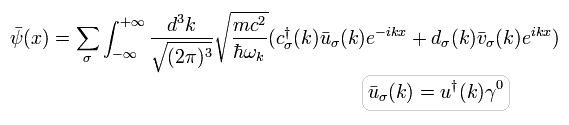
Eq.39, Eq.40 のディラックの波動関数を Eq.38 に代入して、Eq.23 と Eq.24 の 最初と最後の状態を使うと、
(Eq.41)
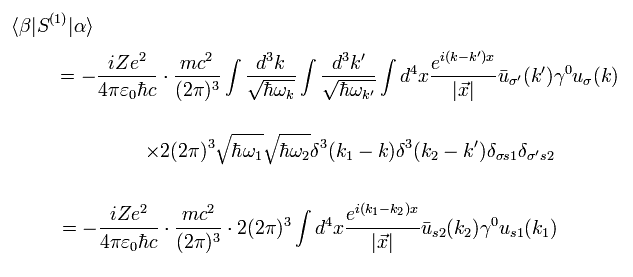
ここでは、 Ap.1 の反交換の関係を使用している。
ここで次の公式を使う。
(Eq.42)
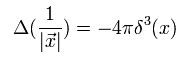
Eq.42 は ガウスの法則を使って証明できる。
(Eq.43)
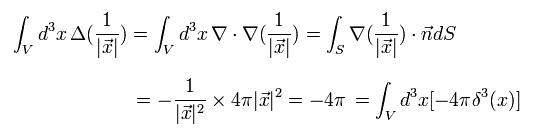
Eq.42 を使って、
(Eq.44)
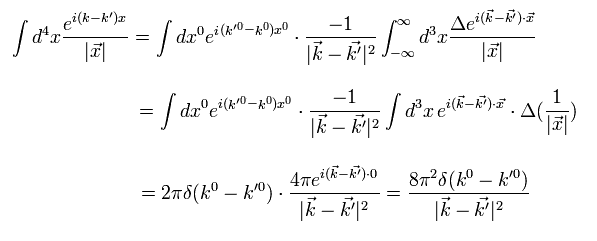
2行目では 部分積分を2回行っている。
Eq.44 を Eq.41 に代入して、
(Eq.45)
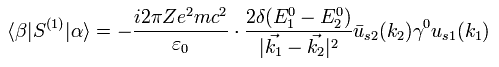
ここで 次の関係式を使う。
(Eq.46)
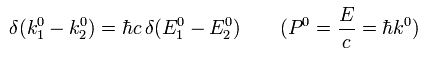
Eq.30 と Eq.45 から、
(Eq.47)
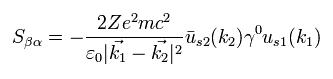
Eq.47 を Eq.37 に代入して、
(Eq.48)
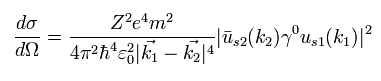
このページに示したように、 次のような トレーステクニックを使うことができる。
(Eq.49)
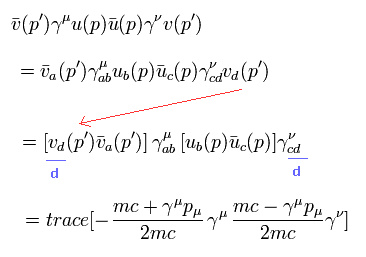
(Eq.50)
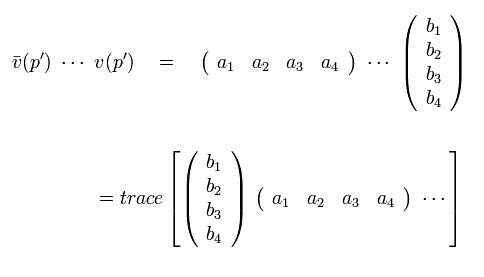
Ap.1 を使って、
(Eq.51)
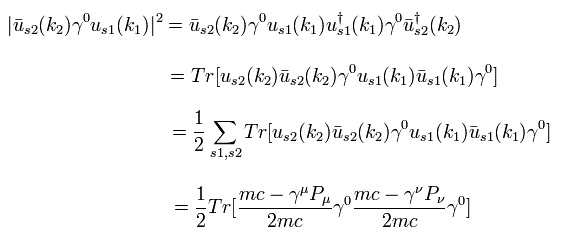
ここで 次を使った。
(Eq.52)
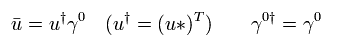
すべてのスピン状態を合計した後、それを2で割っている。 なぜなら 最初の状態のみ2つのスピン状態のどちらか1つのみをとるからである。
( これは思い浮かべるのが難しいかもしれないが、正しい答えを得るのに必要である。 )
ここで ガンマ行列の次のトレース公式を使う。
(Eq.53)
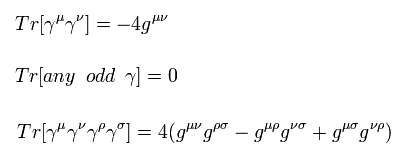
このホームページは (-1, 1, 1, 1) バージョンの軽量テンソルを使用している。
重要な点は 任意の奇数のガンマ行列のトレースはゼロになるということである。
Eq.53 を使って、 Eq.51 の残りの項は、
(Eq.54)
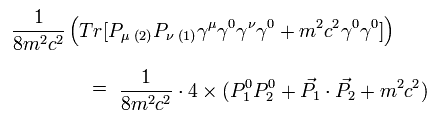
ここでは すべての μ と ν を合計している。
運動量 P1 と P2 の間の角度が θ のとき、
(Eq.55)
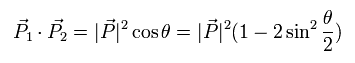
Eq.54 と Eq.55 を Eq.48 に代入して、
(Eq.56)
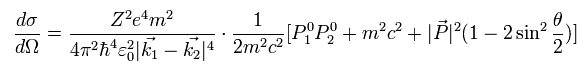
アインシュタインの相対論の公式より、
(Eq.57)
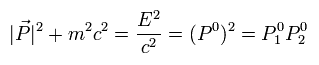
古典力学の Eq.5 のように、
(Eq.58)
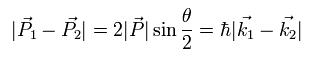
Eq.57 と Eq.58 を Eq.56 に代入して、
(Eq.59)
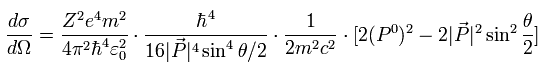
ここで次の関係式を使う。
(Eq.60)
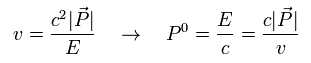
Eq.60 を Eq.59 に代入して、 次の 相対論的な Mott散乱の公式 を得ることができた。
(Eq.61)
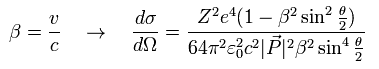
Eq.61 は "相対論" と "スピン"効果 (= γ 行列) を含んでいる。
しかし、残念ながら この”抽象的な”計算過程から 具体的なイメージを思い浮かべることはできない。
あなた方は これらの行列の羅列から、何か思い浮かべることができただろうか?
また、この仮定にはいくつか操作できる部分もあった。
相対論的効果によれば、粒子が速くなるにつれて 重い粒子を加速することがより難しくなる。
しかし このページに見られるように、我々はこの相対論的な質量効果を 電磁場のエーテル理論で”自然に”説明することができる。
Eq.61 の β がゼロに近づき (= 非相対論的近似 )、 また |P| に mv を代入して、
(Eq.62)
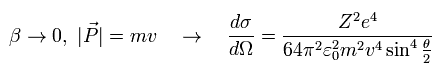
Eq.16 の古典的な ラザフォード公式を得ることができる。

2011/12/29 updated This site is link free.